- Research Article
- Open access
- Published:
An Experimental Evaluation of Foreground Detection Algorithms in Real Scenes
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 373941 (2010)
Abstract
Foreground detection is an important preliminary step of many video analysis systems. Many algorithms have been proposed in the last years, but there is not yet a consensus on which approach is the most effective, not even limiting the problem to a single category of videos. This paper aims at constituting a first step towards a reliable assessment of the most commonly used approaches. In particular, four notable algorithms that perform foreground detection have been evaluated using quantitative measures to assess their relative merits and demerits. The evaluation has been carried out using a large, publicly available dataset composed by videos representing different realistic applicative scenarios. The obtained performance is presented and discussed, highlighting the conditions under which algorithm can represent the most effective solution.
1. Introduction
Several video analysis applications, like intelligent video surveillance or vehicular traffic analysis, require as a preliminary subtask the identification within the scene of the moving objects (foreground of the scene) as opposed to the static parts of the scene (background), since the applications are usually interested only in the presence, position, or trajectory of these objects.
Several methods have been proposed for this foreground detection problem, but none of them is up to now considered as a definitive solution. There are several criteria according to which the foreground detection algorithms could be classified. A possible taxonomy of the main algorithms is the one depicted in Figure 1. As the figure shows, the algorithms fall into two approaches:
-
(i)
derivative algorithms, that work by comparing adjacent frames of the video, under the assumption that foreground objects correspond to rapidly changing areas, while the background is either static or slowly changing;
-
(ii)
background subtraction algorithms, were the current frame of the video is compared with a background model, that is a (usually compact) representation of the set of the possible images observable when the scene does not contain foreground objects.
While both approaches share some similarities, the choice between them has consequences that affect deeply the behavior of the system as a whole, presenting radically different issues and problems.
The class of derivative algorithms can be further divided into three subclasses:
-
(i)
single difference algorithms (e.g., [1–3]), which compare the pixels of the current and the previous frame; pixels whose difference is significant (according to some more or less complex thresholding criterion) are considered part of the background;
-
(ii)
double difference algorithms (e.g., [4, 5]), that consider variations across three or more adjacent frames in order to filter out sudden changes due to image noise;
-
(iii)
optical flow algorithms (e.g., [6]), that estimate the local motion vectors for each pixel or for blocks of pixels, using spatiotemporal derivatives of pixel values or block matching techniques.
The common trait of these methods is that they consider all and only the changing parts of the image as foreground. This yields two kinds of problems. On one hand, sometimes parts of a foreground object (even large parts) do not appear to change, either because the object is momentarily still, or because it has a uniform color and texture, and so its motion determines a pixel change only at its borders. Such areas would then "disappear" from the foreground and be absorbed by the background; this problem is called foreground aperture. On the other hand, sometimes the pixel values of background areas do change, for instance because of lighting variations, or of small uninteresting movements of objects that should be sensibly considered static (e.g., tree leaves moved by the wind). In this case, false foreground objects would be detected by a derivative algorithm.
To avoid these problems, the most common approach is background subtraction. Methods following this approach must keep a description of the background that in the simplest case can be just a reference image, but in more sophisticated algorithms becomes often a quite complex representation, for instance involving a probabilistic modeling of the background pixel values. The comparison with a background model allows the algorithms following this approach to detect foreground objects even when momentarily not moving; also, a complex background model could be able to correctly interpret some changes in the background, such as "waving trees" or predictable lighting changes (e.g., a switch turned on or off). This advantage comes at a cost: the background model must be initialized and, more important, continuously kept up to date to reflect the changes in the observed scene. Background update can be very difficult, often requiring an adequate fraction of the video frames to be uncluttered in order to be performed correctly. This kind of difficulty usually increases with the complexity of the adopted background description. Thus, background subtraction algorithms differ mainly regarding the way they deal with the following questions:
-
(i)
how the background model is represented?
-
(ii)
how the current frame is compared with the background model?
-
(iii)
how the background model is updated after each frame?
From now on, we will concentrate our attention only to background subtraction algorithms. Even focusing on this approach only, many proposed methods exist that give different answers to the above questions. A rough categorization can be done on the basis of the model representation, as shown in Figure 1, considering the following categories:
-
(i)
reference image models (e.g., [7, 8]) represent the background as a single image or, in some methods, as a set of images; the comparison between the background model and the current frame is performed by computing the distance in the color space between the corresponding pixel values; pixels whose distance from the background is above a threshold are assigned to foreground;
-
(ii)
probabilistic models (e.g., [9–14]) represent the background as a probability distribution, using either a parametric approach (typically adopting a Gaussian or Mixture of Gaussians distribution), or a non parametric approach (e.g., a Kernel-Based Estimator); the comparison between the background model and the current frame is performed by computing the probability that each pixel is generated according to the background distribution; pixels whose probability is below a threshold are assigned to foreground;
-
(iii)
neural models (e.g., [15, 16]) represent implicitly the background by means of the weights of a neural network suitably trained on a set of uncluttered frames; the network learns how to classify each pixel into background and foreground.
There is no large consensus in the scientific community on which background subtraction method gives the best results. This is due to the fact that the authors of new methods often provide an evaluation of the effectiveness of their proposals that is inadequate under three respects.
First, new methods are often presented without an experimental comparison with existing ones, so it is not clear if the new methods do really provide any improvement.
Second, experimentation is often performed on few videos (often only a single video!) with a small number of frames (from a few tens to a few hundreds), possibly because of the high cost of examining the results on a long video; this introduces a bias in the results, since a single video cannot be representative of many real-life situations, and if the video is short many problems found in real applications cannot be reproduced (e.g., the change of lighting due to the passing of time).
A third inadequacy is that often the experimental results are given in a qualitative way, without a quantitative measurement of the improvement due to the proposed algorithm; this is often motivated by the lack of universally accepted quantitative performance indices for foreground recognition, and by the excessive cost of producing a ground truth (e.g., a dataset accompanied by the desired, ideal output of a foreground detection system) for large videos.
For these reasons, it is not easy for a researcher developing a video analysis application to choose which foreground detection technique is the most appropriate for the application domain at hand, and so often an out of date algorithm is used because of its simplicity or of the availability of an already tested implementation. However it would be very useful if some more reliable information were available on the actual performance advantages of one algorithm over another; especially if these advantages were measured quantitatively and on a realistic dataset.
The aim of this paper is to provide a first step in this direction: four background subtraction algorithms, representative of the most commonly used techniques, have been experimentally evaluated. For the evaluation, a large dataset has been assembled, comprising both well known, publicly available videos and new videos realized for the purpose of this experimentation. The whole dataset, including the ground truth, has been made available on the web, to allow other researchers to extend our experiment to other algorithms. In order to compare the considered algorithms, a set of quantitative performance indices have been selected, adapting measures commonly used for detection systems to the peculiarities of foreground detection.
The remaining sections of the paper are organized as follows: in Section 2, the selected algorithms will be briefly described. Section 3 will provide a description of the dataset used for this experimentation and of the performance indices, followed by the presentation and discussion of the results obtained by each algorithm. Finally, some conclusions will be drawn and some possible future works will be sketched.
2. Algorithms Description
For our comparative evaluation, we considered the following algorithms:
-
(i)
the Mixture of Gaussians (from now on called MOG), in the version proposed by Kaewtrakulpong and Bowden in [12];
-
(ii)
the Enhanced Background Subtraction (from now on EBS), proposed by Conte et al. in [8];
-
(iii)
the Self-Organizing Background Subtraction (from now on SOBS), proposed by Maddalena and Petrosino in [16];
-
(iv)
the Statistical Background Algorithm (from now on SBA), proposed by Li et al. in [17].
These algorithms have been chosen because they are representative of each category of background subtraction methods, being based on a probabilistic model (MOG, SBA), on a reference image model (EBS) and on a neural model (SOBS). In particular, MOG is definitely the most cited among the algorithms adopting a statistical approach, and has been used as a component of many larger systems. Although SBA is not as popular as MOG, it is one of the most cited algorithms, in recent papers, among the ones using a Bayesian approach. EBS has been chose because, despite being quite similar to the "archetypical" reference image technique, it had shown in previous experiments [8] a very good performance. Finally, since among the class of neural methods we have not found anyone that was clearly emerging for the number of references to it, we have chosen SOBS as a representative since it is very recent and in the experiments reported by its authors [16] appeared to attain a good performance level.
As representatives of the background subtraction approach, these four methods share a common overall structure: they keep a background model that is built when the scene does not contain objects of interest. The current frame is compared with the background model, and the pixels that differ significantly from the model are considered part of objects to be detected (foreground pixels). Then, after the object detection, the background model is updated to reflect changes in the observed scene (e.g., lighting changes).
2.1. The MOG Algorithm
The first algorithm we consider, the Mixture of Gaussians Algorithm, is one of the most used ones in object detection systems. The original version of this algorithm has been introduced by Stauffer and Grimson in [11]. We will, however, refer to the improved version by Kaewtrakulpong and Bowden described in [12].
In this algorithm, each image pixel is modeled using a mixture of  Gaussian distributions (where
Gaussian distributions (where  is a small natural number, usually from 3 to 5). Each Gaussian represents with its mean one of the colors that the pixel may assume, and with its variance the fluctuations of the actual color values around the mean. Each Gaussian also has a weight, corresponding to the fraction of time that the pixel has shown a color corresponding to that Gaussian in its past history.
is a small natural number, usually from 3 to 5). Each Gaussian represents with its mean one of the colors that the pixel may assume, and with its variance the fluctuations of the actual color values around the mean. Each Gaussian also has a weight, corresponding to the fraction of time that the pixel has shown a color corresponding to that Gaussian in its past history.
The basic assumption of the method is that a pixel is occupied by background objects more frequently than by foreground ones. So the  Gaussians (with
Gaussians (with  ) corresponding to the largest time fractions will model background colors, while the remaining ones will model foreground colors. Having multiple distributions for modeling the background, makes the algorithm able to deal with situations as waving trees, or a door/window can be opened or closed, or fast repeated light changes, such as an electric light turned on and off. Foreground detection is performed as follows:
) corresponding to the largest time fractions will model background colors, while the remaining ones will model foreground colors. Having multiple distributions for modeling the background, makes the algorithm able to deal with situations as waving trees, or a door/window can be opened or closed, or fast repeated light changes, such as an electric light turned on and off. Foreground detection is performed as follows:
-
(i)
for each pixel, its color in the current frame is compared to
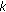 Gaussian distributions, and the one that maximizes the probability of producing that color is selected;
Gaussian distributions, and the one that maximizes the probability of producing that color is selected; -
(ii)
if the selected Gaussian is one of the
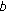 most probable ones, and the distance of the color from the Gaussian mean is within 2.5 times the standard deviation, the pixel is considered as a background pixel; otherwise it is considered as a foreground one;
most probable ones, and the distance of the color from the Gaussian mean is within 2.5 times the standard deviation, the pixel is considered as a background pixel; otherwise it is considered as a foreground one; -
(iii)
if the distance of the color from the Gaussian mean is within 2.5 times the standard deviation, the selected Gaussian parameters and weight are updated; otherwise, a new Gaussian is created replacing the one with the smallest weight.
The update phase is critical, in order to allow the algorithm to adapt to lighting changes; it also plays an essential role in the initial construction of the background model. This is an aspect where the algorithms presented in [11, 12] differ: the first algorithm simply performs an exponential moving average, while the second uses an update equation that learns faster in the initial phase (when the model is being initialized), and then converges to a slower learning rate subsequently.
Furthermore, [12] also introduces a shadow detection algorithm integrated in the method. The shadow detection computes a distance between the color of the pixel and each of the background model distribution, treating separately the luminance of the pixel and its chrominance. The luminance and chrominance differences are then compared with two thresholds: if the pixel is chromatically very similar to a background distribution, and its luminance is lower (within a threshold), it is considered as a shadow pixel, and it is neither included in the detected foreground, nor used to update the background model.
2.2. The SBA Algorithm
The Statistical Background Algorithm, proposed by Li et al. in [17], is based on a Bayesian decision rule that takes into account the possibility of background moving objects and is able to address sudden "once-off" changes of the scene.
The algorithm is divided into four phases: change detection, change classification, foreground object, segmentation and background learning/maintenance.
The first phase, change detection, is aimed at dividing the pixel into motion pixels and stationary pixels. Both types of pixels may belong to either foreground or background objects (the algorithm considers both moving background objects and stationary foreground objects). Thus, the distinction between motion and stationary pixels is only performed in order to use a different, more specific classifier for each category in the following phase. Change detection uses the temporal difference between two adjacent frames, together with an adaptive thresholding, to decide whether a pixel should be considered in motion or stationary.
In the second phase, change classification, pixels are classified into foreground and background pixels. For stationary pixels, the decision is based on the current pixel color, while for motion pixels the algorithm uses the color cooccurrence vector representing the combination of pixel colors at the current frame and at the previous one. In both cases, the used information is encoded as a feature vector whose probability is estimated by a Bayesian decision rule, using a table of feature statistics; for stationary pixels the feature statistics are conditioned on the pixel value of a background reference image.
In the third phase, foreground object segmentation, the foreground pixels are grouped into objects, by applying morphological operators to filter out scattered error points and then finding the connected components. Objects whose pixel count is under a threshold are discarded.
In the fourth and final phase, background learning and maintenance, the algorithm updates both the background reference image and the tables of feature statistics. The update algorithm is able to recognize if a massive change of the background is taking place (a "once-off" background change); when this happens, the update rule is modified to quickly integrate the observed changes in the background model.
According to the authors of [17], the method is implicitly able to filter out shadows, since the statistics of the shadow features are incorporated in the background model.
2.3. The SOBS Algorithm
The Self-Organizing Background Subtraction algorithm is a recent method proposed by Maddalena and Petrosino in [16]. The basic idea of the method is the use of a neural network, based on the Self-Organizing Map paradigm, to represent the background model.
More precisely, the model is encoded on a 2D grid of nodes, where each background pixel corresponds to a  subregion of the grid (
subregion of the grid ( is a parameter of the algorithm). Thus each pixel is represented by
is a parameter of the algorithm). Thus each pixel is represented by  nodes. Each node maintains as its weight vector a possible color for the background pixel, encoded in the Hue-Saturation-Value (HSV) color space.
nodes. Each node maintains as its weight vector a possible color for the background pixel, encoded in the Hue-Saturation-Value (HSV) color space.
During the training phase of the algorithm, which lasts for the first  frames, with
frames, with  chosen so as to have only background objects in those frames, the network operates as follows:
chosen so as to have only background objects in those frames, the network operates as follows:
-
(i)
for each pixel, the node with the weight vector most similar to the pixel HSV color is chosen among the
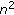 nodes associated with the pixel (winning node);
nodes associated with the pixel (winning node); -
(ii)
the weight vector of the winning node is updated so as to be closer to the HSV color of the actual pixel; this update is also performed on the nodes that occupy a neighboring position on the grid (nodes that may also belong to different pixels), moving their weight vectors by an amount that decreases as their grid distance from the winning node increases.
So this process produces a model for each pixel that is influenced both by the different colors the pixel assumed during the training phase, and by the colors of the neighboring pixels.
During the operation phase, the network operates in a slightly more complex manner:
-
(i)
like before, for each pixel, the node with weight vector most similar to the pixel HSV color is chosen among the
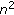 nodes associated with the pixel (winning node);
nodes associated with the pixel (winning node); -
(ii)
if the distance between the pixel HSV color and the winning node weight vector is under a given threshold, the pixel is considered as a background pixel, and the network nodes are updated as in the training phase;
-
(iii)
if the pixel color is close to the winning node weight vector in the Hue and Saturation components, but differs significantly in the Value (intensity), and the pixel Value is darker than the node Value component, the pixel is considered as a shadow pixel, and ignored (node update does not take place);
-
(iv)
otherwise, the pixel is considered as a foreground pixel; in this case, too, the background model is not updated.
The learning rate, that is, the speed of the change of the weight vectors of the updated nodes, is defined as a decreasing function (with respect to the number of frames) during the training phase, while it remains constant (at a lower value) during the operation phase.
As it can be noted, the algorithm explicitly takes into account shadows, using the assumption that shadow pixels are of a darker shade of the same color of the corresponding background.
2.4. The EBS Algorithm
The Enhanced Background Subtraction algorithm, presented in [8], is an improvement of the basic background subtraction technique, with enhancements that address several problems often encountered in outdoor scenes, where lighting conditions can show quite large variations.
This method differs from the others presented in the previous sections in that it uses a rather simple background model (just a reference image); instead of defining a complex model (that could be hard to learn reliably), the method attempts to exploit as much as possible the basic background model by introducing a set of enhancements in the operations that deal with the model.
The enhancements with respect to basic background subtraction fall in three areas: thresholding, shadow removal, and reference image update.
For thresholding, a dynamic strategy is proposed to adaptively select the most appropriate threshold in the comparison between the current frame and the reference image. Basically, a feedback is introduced that increases or decreases the threshold value on the basis of a global measure on the current frame.
As regards shadow removal, this method does not assume a color model of the shadow pixels. Instead, it is based on a model of the shape of a shadow and of its relation to the object that casts it. So, shadow removal takes place after a first, tentative foreground detection: the parts of the tentative foreground that are consistent with the shadow model are removed, obtaining the final foreground image.
For the update of the reference image, two different IIR filters are used: a fast converging one, applied to the areas recognized as background, to quickly adapt to sudden lighting changes; and a slowly converging one, applied to the foreground areas, to incorporate in the background model objects that become stationary (e.g., a parked car). Another enhancement regarding the reference image update is that the algorithm attempts to predict the changes in the background areas occluded by foreground objects on the basis of the observed changes in the unoccluded background areas; the predicted changes are applied to the reference image. This is very useful for dealing with slowly moving objects, since it avoids the formation of "ghost" objects due to the fact that, after the real object has moved away, the observed background behind it has become too different from the one recorded in the reference image.
3. Algorithms Comparison
3.1. The Dataset
In order to compare the performance of the selected algorithms, the first step required is the construction of a suitable data set. For our experiments, we have used seven videos (see Figure 2); four of them were already publicly available, while the remaining three have been realized for this evaluation, and have been made available, complete with the ground truth, on the web at the address given in [18]. In Table 1, an overview of the characteristics of each video is presented.
The use of several videos allowed us to characterize the performance of the algorithms in different conditions, since each condition is affected by its own, peculiar set of problems. Using a single video, it would have been quite difficult to reproduce all the problems that an object detection method has to face in a real world setting.
Video MIVIA1 has been acquired in a large square in Naples, in a sunny day, with several persons walking. The main difficulty in this kind of scene is the presence of very dark, definite shadows; if they are not properly removed, they cause the merge of several distinct objects in the scene.
Video MIVIA2 has been acquired in the same place as MIVIA1, but with very different weather conditions: a very cloudy day. As a consequence, in MIVIA2 there are almost no shadows. On the other hand, the difficulty of this video is that, under such light conditions, the colors tend to get flattened, and so it becomes more likely that parts of a foreground object are confused with the background behind it (camouflage). As a results, objects are often split into pieces by the algorithms.
In video MIVIA3, the scene is the same of the previous two videos, but with yet another lighting condition: the video has been acquired very late in the afternoon. So the shadows are very long, although not as dark and definite as in MIVIA1, and the bias on the colors induced by the sunset light also causes a fair amount of camouflage. Furthermore, the length of the video is sufficient to evaluate the ability of the algorithms to deal with light changes due to the passing of time.
Video PETS2006 is a subsequence of the dataset published at the 2006 edition of the PETS workshop. Reflection problems are the main difficulty of this video; while the objects of interest are easily detected, the algorithms are usually unable to remove the reflections from the detected foreground.
Videos PETS2009-1 and PETS2009-2 have been chosen among the video sequences published at the 2009 edition of the PETS workshop (in particular, they are the sequences labeled S1-L1-3-57 and S1-L1-14-06). These videos contains a moderately crowded scene, with many occlusions.
Finally, the MSA video shows an indoor scene where a person leaves a rucksack on the floor. The main problem of this video is constituted by the vertical shadows.
3.2. The Performance Indices
In the literature, there have been much efforts to evaluate the performance of the tracking algorithms, whereas similar results have not been obtained for the assessment of the performance with respect to the problem of object detection. One reason is the huge effort needed to produce the ground truth that would require to determine for each pixel of each frame if it belongs to the foreground or the background. Here we use a quantitative method, widely adopted in the context of information retrieval systems. To measure the effectiveness of detection systems the precision and recall figures of merit are often used. They are defined as follows:

where  ,
,  and
and  are, respectively, the True Positives, False Positives, and False Negatives. Since in the object detection problem the answer is not a simple "yes" or "no" value (an object could be detected partially, or conversely part of the background could be attributed to the object), a fuzzy definition of True Positives, False Positives and False Negatives is needed. We have chosen the following definitions:
are, respectively, the True Positives, False Positives, and False Negatives. Since in the object detection problem the answer is not a simple "yes" or "no" value (an object could be detected partially, or conversely part of the background could be attributed to the object), a fuzzy definition of True Positives, False Positives and False Negatives is needed. We have chosen the following definitions:

where  and
and  are respectively the set of objects in the ground truth and the set of objects detected by the algorithm (each object is represented by its bounding box); with
are respectively the set of objects in the ground truth and the set of objects detected by the algorithm (each object is represented by its bounding box); with  and
and  we denote the intersection and the union of two boxes, while
we denote the intersection and the union of two boxes, while  indicates the area of a region.
indicates the area of a region.
Sometimes it is preferable to have one single index for measuring the performance (e.g., for performance tuning of a parametric system); in this case some authors propose the  -score, defined as the harmonic mean of precision and recall:
-score, defined as the harmonic mean of precision and recall:

3.3. Experimental Results and Discussion
The values of the precision, recall and  -score indices obtained by the considered algorithms over the 7 datasets are summarized in Table 2.
-score indices obtained by the considered algorithms over the 7 datasets are summarized in Table 2.
 -score for any video.
-score for any video.The EBS algorithm is very effective in most of the cases (e.g., see Figure 3, Figure 4, and Figure 5) and obtains, on 5 of the 7 videos, the best results among the tested methods. The algorithm attains a high value of the performance indices on all the videos, with the remarkable exception of the recall index for video MIVIA3, due to the excessive presence of camouflage that results in several split objects, and of the precision index for video MIVIA1, due to the extremely dark shadows that are sometimes classified as foreground objects (this problem is common to all the tested algorithms).
Effective results are also obtained using the MOG algorithm, that shows a fairly uniform performance over the different videos (e.g., see Figure 3, Figure 4, and Figure 5). An exception to this uniformity is the result on the MSA video, where the precision of MOG is significantly lower than that of the other algorithms. It seems that on this video the learning of the background model does not converge to an accurate distribution, likely because there is an insufficient number of frames without foreground objects.
Performance of the SBA algorithm is quite low on the average, with the exception of the two PETS2009 videos, despite the significant effort spent in tuning the algorithm parameters. Precision is usually low (the algorithm detects many false positives), while recall is acceptable or even good; only on the MIVIA3 and MSA videos recall becomes unacceptably low. For MIVIA3 the problem is due to camouflage, while for MSA the algorithm does not manage to correctly construct the tables of feature statistics, also in this case because there is an insufficient number of frames without foreground object.
Similarly to SBA, also the SOBS algorithm proved to be difficult to set up. The algorithm performs very well in an indoor setting (the MSA video; e.g., see Figure 5). On the other hand, performance is not so good on outdoor videos, especially on the three MIVIA videos and on PETS2006. Usually the algorithm has a medium-to-good recall; instead, the precision is adequate only on the PETS2009 videos and on MSA. The fact that on MSA this algorithm outperforms the others is likely due to its model initialization technique, that is able to rapidly build a background model from few uncluttered frames.
4. Conclusions
The choice of the right foreground detection algorithm is not easy without the availability of an extensive, quantitative benchmark that relates the advantages and disadvantages of each algorithm to the characteristics of the observed scene. As a first step towards this aim, we have performed an experimental comparison of four object detection algorithms (representative of the most common approaches), using quantitative performance indices, on a large dataset of videos covering several realistic applicative scenarios.
From our experiments, it resulted that both the MOG and the EBS algorithms are quite versatile and can be used effectively in most situations. Between the two, EBS has some more problems with camouflage, while MOG has problems when there are not enough uncluttered frames to learn the background model. The SOBS algorithm gives good results in indoor environments, but can have some problems in outdoor settings. Finally, SBA is almost always outperformed by the others, so its adoption does not seem advisable.
As a future work, it would be very useful to extend this comparative evaluation to other algorithms. To this aim, the video database used for the experiments, together with the associated ground truth, has been made publicly available. Also, we are currently planning to extend this database with more videos having different characteristics.
Furthermore, given the insight gained on the strengths and the weaknesses of each considered algorithm, some research will be devoted to investigate the possibility of combining ideas taken from different algorithms to attain a further improvement of their effectiveness.
References
Li L, Leung MKH: Integrating intensity and texture differences for robust change detection. IEEE Transactions on Image Processing 2002, 11(2):105-112. 10.1109/83.982818
Aach T, Kaup A, Mester R: Statistical model-based change detection in moving video. Signal Processing 1993, 31(2):165-180. 10.1016/0165-1684(93)90063-G
Archetti F, Manfredotti C, Messina V, Sorrenti D: Foreground-to-ghost discrimination in single-difference preprocessing. Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems, 2006
Xia J, Wu J, Zhai H, Cui Z: Moving vehicle tracking based on double difference and camshift. Proceedings of the International Symposium on Information Processing, 2009
Collins R, Lipton A, Kanade T, et al.: A system for video surveillance and monitoring. Robotics Institute, Pittsburgh, Pa, USA; May 2000.
Horn BKP, Schunck BG: Determining optical flow. Artificial Intelligence 1981, 17(1–3):185-204.
Toyama K, Krumm J, Brumitt B, Meyers B: Wallflower: principles and practice of background maintenance. Proceedings of the 7th IEEE International Conference on Computer Vision (ICCV '99), September 1999 1: 255-261.
Conte D, Foggia P, Petretta M, Tufano F, Vento M: Meeting the application requirements of intelligent video surveillance systems in moving object detection. In Proceedings of the 3rd International Conference on Advances in Pattern Recognition and Image Analysis, 2005, Bath, UK, Lecture Notes in Computer Science. Volume 3687. Springer; 653-662.
Wren CR, Azarbayejani A, Darrell T, Pentland AP: Pfinder: real-time tracking of the human body. IEEE Transactions on Pattern Analysis and Machine Intelligence 1997, 19(7):780-785. 10.1109/34.598236
Haritaoglu I, Harwood D, Davis LS: W4: real-time surveillance of people and their activities. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 22(8):809-830. 10.1109/34.868683
Stauffer C, Grimson WEL: Learning patterns of activity using real-time tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 22(8):747-757. 10.1109/34.868677
Kaewtrakulpong P, Bowden R: An improved adaptive background mixture model for realtime tracking with shadow detection. Proceedings of the 2nd European Workshop on Advanced Video Based Surveillance Systems (AVBS '01), 2001
Elgammal A, Duraiswami R, Harwood D, Davis LS: Background and foreground modeling using nonparametric kernel density estimation for visual surveillance. Proceedings of the IEEE 2002, 90(7):1151-1162. 10.1109/JPROC.2002.801448
Kim K, Chalidabhongse TH, Harwood D, Davis L: Real-time foreground-background segmentation using codebook model. Real-Time Imaging 2005, 11(3):172-185. 10.1016/j.rti.2004.12.004
Ćulibrk D, Marques O, Socek D, Kalva H, Furht B: Neural network approach to background modeling for video object segmentation. IEEE Transactions on Neural Networks 2007, 18(6):1614-1627.
Maddalena L, Petrosino A: A self-organizing approach to background subtraction for visual surveillance applications. IEEE Transactions on Image Processing 2008, 17(7):1168-1177.
Li L, Huang W, Gu IYH, Tian Q: Foreground object detection from videos containing complex background. Proceedings of the 11th ACM International Conference on Multimedia (MM '03), November 2003 2-10.
University of Salerno—Lab. of Intelligent Machines for Video, Image and Audio Analysis : Video database. http://www.adinf.unisa.it/zope/home/mivia/databases/db_database
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Conte, D., Foggia, P., Percannella, G. et al. An Experimental Evaluation of Foreground Detection Algorithms in Real Scenes. EURASIP J. Adv. Signal Process. 2010, 373941 (2010). https://doi.org/10.1155/2010/373941
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/373941

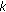 Gaussian distributions, and the one that maximizes the probability of producing that color is selected;
Gaussian distributions, and the one that maximizes the probability of producing that color is selected;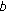 most probable ones, and the distance of the color from the Gaussian mean is within 2.5 times the standard deviation, the pixel is considered as a background pixel; otherwise it is considered as a foreground one;
most probable ones, and the distance of the color from the Gaussian mean is within 2.5 times the standard deviation, the pixel is considered as a background pixel; otherwise it is considered as a foreground one;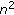 nodes associated with the pixel (winning node);
nodes associated with the pixel (winning node);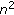 nodes associated with the pixel (winning node);
nodes associated with the pixel (winning node);


