- Research Article
- Open access
- Published:
A New Robust Watermarking Scheme to Increase Image Security
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 428183 (2010)
Abstract
In digital image watermarking, an image is embedded into a picture for a variety of purposes such as captioning and copyright protection. In this paper, a robust private watermarking scheme for embedding a gray-scale watermark is proposed. In the proposed method, the watermark and original image are processed by applying blockwise DCT. Also, a Dynamic Fuzzy Inference System (DFIS) is used to identify the best place for watermark insertion by approximating the relationship established between the properties of HVS model. In the insertion phase, the DC coefficients of the original image are modified according to DC value of watermark and output of Fuzzy System. In the experiment phase, the CheckMark (StirMark MATLAB) software was used to verify the method robustness by applying several conventional attacks on the watermarked image. The results showed that the proposed scheme provided high image quality while it was robust against various attacks, such as Compression, Filtering, additive Noise, Cropping, Scaling, Changing aspect ratio, Copy attack, and Composite attack in comparison with related methods.
1. Introduction
Owing to the recent advances in network and multimedia techniques, digital images may be transmitted over the nonsecure channels such as the Internet. Therefore, the enforcement of multimedia copyright protection has become an important issue in literature.
Watermarking and cryptography are two standard multimedia security methods. However, cryptography is not an effective method because it does not provide permanent protection for the multimedia content after delivery to consumers, because, after decryption there is no protection for the documents. Digital watermarking technologies allow users to hide appropriate information in the original image that is imperceptible during normal use but readable by special application. Therefore, the major purpose of digital watermarks is to provide protection for intellectual property that is in digital format. To evaluate a watermark system, the following attributes are generally considered [1, 2].
-
(1)
Readability. A watermark should convey as much information as possible, statistically detectable, enough to identify ownership and copyright unambiguously.
-
(2)
Security. Only authorized users gain access to the watermark data.
-
(3)
Imperceptibility. The embedding process should not introduce any perceptible artifacts into original image and not degrade the perceived quality of image.
-
(4)
Robustness. The watermark should be able to withstand various attacks while can be detected in the extraction process.
The most important watermarking schemes are invisible where are secure and robust. Moreover, in the invisible watermarking, the embedding locations are secret, and only the authorized persons who have the secret keys can extract the watermark.
On the other hand, the watermarking algorithms are classified also as: the methods which require the original information and secret keys for extracting watermark are called private watermark algorithms. The methods which require the watermark information and secret keys are called semiprivate or semiblind algorithms, and ones which need secret keys rather than the original information are called blind watermark algorithms.
In another classification, digital watermarking algorithms can be divided into two groups: spatial domain [5–7] and frequency domain [8–12] methods according to the processing domain of the host image. The spatial domain algorithms are simple and the watermark can be damaged easily, but the frequency domain algorithms can resist versus intensity attack and watermark information cannot be damaged easily [13].
However, in all frequency domain watermarking schemes, there is a conflict between robustness and transparency. If the watermark is embedded in the lower-frequency bands, the scheme would be robust to attacks but the watermark may be difficult to hide. On the other hand, if the watermark is embedded in the higher-frequency bands, it would be easier to hide the watermark but the scheme has less resistant to attacks. Therefore, finding a proper place to embed the watermark is very important.
In 1996, Cox et al. [14] advised that the watermark should be embedded in the low-frequency coefficients of DCT domain to ensure the robustness. To improve this method, Lu et al. [15] used a cocktail watermark to increase robustness and HVS to maintain high fidelity of the watermarked image. Barni and Hsu [16, 17], respectively, recommended that the watermark should be embedded in the middle frequency coefficients to reduce the distortion. But Huang et al. in [18] points out that the DC coefficient is more proper to be used for embedding watermark, and this conclusion is obtained based on his robustness test between the DC coefficient and two low-frequency coefficients.
Also, DWT as another frequency transform technique has been used by many researchers such as Xie and Arce for digital image watermarking [19]. The proposed method by Zhao et al. in [20] is a sample of DCT/DWT domain-based method which uses a dual watermarking scheme exploiting the orthogonality of image subspaces to provide robust authentication. As other examples, in [21, 22], the proposed DCT/DWT methods embed a binary visual watermark by modulating the middle-frequency components. These two methods are robust to common image attacks; but geometric attacks are still challenges. In [23], another approach to combine DWT and DCT has been proposed to improve the performance of the DWT-based watermarking algorithms. In this method, watermarking is done by embedding the watermark in the first and second level of DWT subbands of the host image, followed by the application of DCT on the selected DWT subbands. The combination of these two transforms improved the watermarking performance considerably in comparison with DWT-only watermarking approach.
Most of the existing watermarking methods use a pseudorandom sequence or binary image as a watermark. However, using grayscale images as watermarks has drawn much attention for copyright protection since many logos are grayscale in nature. One of the methods that hide a grayscale watermark image in original image was proposed by Mahanty and Bhargava [24]. In this method, at first, based on Human Visual System (HVS), the most perceptually important region of original image is found. Then, a compound watermark is created to insert in this region of the original image. For creation of compound watermark, the synthetic image is created by Gaussian and Laplacian random number generator. The choice of these two distributions for modeling the DC and AC coefficients of image DCT is motivated by empirical results presented in Reininger and Gibson [25] and Mohanty et al. [26]. Next, the original watermark is embedded in insensitive area of synthetic image using any DCT-based visible watermarking algorithm. Asatryan proposed another method that combines spatial and frequency domain to hide a grayscale watermark in grayscale original image by mapping the values of DCT coefficients of compressed watermark image to the interval [0,255] (max and min value of grayscale image) by a fixed linear transform and inserts these values in the original image [27]. But, this method introduces perceptible artifacts into original image and degrades the perceived quality of image.
In this paper, we have proposed a new robust watermarking method in frequency domain to insert a gray level watermark in an image. The proposed method is more robust and makes image with higher quality than related ones. The basic idea of the proposed method is based on this fact that most of the signal energy of the DCT block is compacted in the DC component and the remaining energy is distributed reductively in the AC components in zigzag scan order [4]. Also, for most images, the main characteristics of the DCT coefficients in one block have high correlation with the adjacent blocks. Gonzales et al. [3] described a technique which estimates the first five AC coefficients precisely. In this method, DC values of a  neighborhood of blocks are used to estimate the AC coefficients for the center block. They did not consider variations in the image in AC coefficients estimation, but Veeraswamy and Kumar in [4] proposed a new method that considered the variation in the image and accordingly AC coefficients have been estimated with different equations. This method is better than Gonzales method in terms of reduced blocking artifacts and improved PSNR value. Based on these ideas, here, at first, a grayscale watermark image is created by applying DCT on each
neighborhood of blocks are used to estimate the AC coefficients for the center block. They did not consider variations in the image in AC coefficients estimation, but Veeraswamy and Kumar in [4] proposed a new method that considered the variation in the image and accordingly AC coefficients have been estimated with different equations. This method is better than Gonzales method in terms of reduced blocking artifacts and improved PSNR value. Based on these ideas, here, at first, a grayscale watermark image is created by applying DCT on each  nonoverlapping block of original grayscale watermark image and setting all AC coefficients of each one to zero. Then, the original image is divided into
nonoverlapping block of original grayscale watermark image and setting all AC coefficients of each one to zero. Then, the original image is divided into  nonoverlapping blocks and DCT is applied on each
nonoverlapping blocks and DCT is applied on each  block. Next, a Dynamic Fuzzy Inference System (DFIS) is used to select the number of original image blocks for embedding watermark. Finally, DC value of each
block. Next, a Dynamic Fuzzy Inference System (DFIS) is used to select the number of original image blocks for embedding watermark. Finally, DC value of each  DCT block of watermark image is embedded in DC value of
DCT block of watermark image is embedded in DC value of  DCT block of original image by using the output of the DFIS. In the extraction process, DCT is applied on the test image to extract the DC coefficients of each
DCT block of original image by using the output of the DFIS. In the extraction process, DCT is applied on the test image to extract the DC coefficients of each  DCT block of watermark and the AC coefficients of each
DCT block of watermark and the AC coefficients of each  DCT block of extracted watermark are estimated based on proposed technique by Veeraswamy and Kumar [4] to construct the watermark with higher quality. The proposed method was tested on several bench mark images using StirMarkMATLAB software and its results were satisfactory. The results showed that the proposed method created the high-quality watermarked images while they were more robust against attacks such as JPEG compression, additive noise, filtering, cropping.
DCT block of extracted watermark are estimated based on proposed technique by Veeraswamy and Kumar [4] to construct the watermark with higher quality. The proposed method was tested on several bench mark images using StirMarkMATLAB software and its results were satisfactory. The results showed that the proposed method created the high-quality watermarked images while they were more robust against attacks such as JPEG compression, additive noise, filtering, cropping.
The rest of paper has been organized as follows: In Section 2, the proposed approach has been introduced and in Section 3, the proposed method has been motivated and structurally compared with related ones. Section 4 describes the experimental results and in Section 5, the paper has been concluded.
2. Proposed Algorithm
In this section, the proposed algorithm is describedin detail. The algorithm is divided into four parts: block selection, watermark creation,watermark embedding and watermark extraction, which are described in Sections 2.1–2.4, respectively.
2.1. Block Selection
In this section, we try to find the best blocks for embedding the watermark. For this purpose, the original image is divided to  nonoverlapping blocks and subsequently DCT is applied on each block. In the following of this paper, the value of
nonoverlapping blocks and subsequently DCT is applied on each block. In the following of this paper, the value of  is considered as 8 to increase the method robustness versus compression because the standard JPEG is based on
is considered as 8 to increase the method robustness versus compression because the standard JPEG is based on  blocks. Then, the following properties of Human Visuals System (HVS) model that is suggested in [24, 28] is used for selecting blocks that are suitable for embedding watermark.
blocks. Then, the following properties of Human Visuals System (HVS) model that is suggested in [24, 28] is used for selecting blocks that are suitable for embedding watermark.
-
(i)
Luminance Sensitivity(
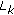 ). The brighter the background, the lower the visibility of the embedded watermark. It is estimated by following relation:
). The brighter the background, the lower the visibility of the embedded watermark. It is estimated by following relation: 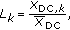 (1)
(1)where
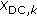 is the DC coefficient of
is the DC coefficient of 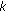 th block and
th block and 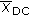 is the mean value of DC coefficients of an original image.
is the mean value of DC coefficients of an original image. -
(ii)
Texture Sensitivity(
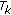 ). The stronger the texture, the lower visibility of embedded watermark. It can be estimated by quantizing the DCT coefficients of a block
). The stronger the texture, the lower visibility of embedded watermark. It can be estimated by quantizing the DCT coefficients of a block 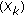 using the JPEG quantization table
using the JPEG quantization table 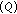 . The latter results are then rounded to the nearest integers. The number of nonzero coefficients is then computed. This number presents the texture of that block:
. The latter results are then rounded to the nearest integers. The number of nonzero coefficients is then computed. This number presents the texture of that block: 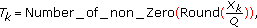 (2)
(2)where
 are coefficients and
are coefficients and  counts nonzero coefficients in
counts nonzero coefficients in 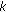 th block.
th block. -
(iii)
Location Sensitivity(
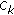 ). The center quarter of an image is perceptually more important than other areas of the image. We estimate location of each block by computing the following ratio:
). The center quarter of an image is perceptually more important than other areas of the image. We estimate location of each block by computing the following ratio:  (3)
(3)
where  is the number of pixels of the
is the number of pixels of the  th block lying in the center quarter (25%) of the image.
th block lying in the center quarter (25%) of the image.
When these parameters are computed, they can be used to select blocks and determine weighting factor for embedding. In the proposed method, a Fuzzy Inference System (FIS) for calculating the relationship established between all properties of the HVS model is used because FIS provides simple mapping from a given set of inputs to another set of outputs without the complexity of mathematical modeling concepts.
Here, a DFIS has been used [28] and optimized in order to approximate the relationship established between three properties of the HVS model for both block selection and embedding process. We supposed the location sensitivity parameter is independent to images, therefore, in this model a static membership function is used for location sensitivity and only texture sensitivity and luminance sensitivity have dynamic membership functions. In the proposed DFIS, as it is shown in Figure 1, the inputs consist of texture sensitivity, luminance sensitivity, and location sensitivity parameters of each block and the outputs consist of corresponding suitability and weighting factors. The shape and support set values for inputs and outputs MFs (Membership functions) have been derived from experiments on various images.
The suitability parameter (α) depends to all three inputs but the weighting factor (β) only depends on the texture sensitivity and luminance sensitivity. Let now explain for instance how the texture sensitivity membership function is computed. The structure of Texture sensitivity membership function has been shown in Figure 2. To compute the membership function parameters; first, we set  and
and  to take the minimum and maximum values of texture sensitivity
to take the minimum and maximum values of texture sensitivity  (4):
(4):

where  is the Texture sensitivity of the
is the Texture sensitivity of the  th block of the image. Then, in order to find point
th block of the image. Then, in order to find point  , the average of the texture sensitivity of all
, the average of the texture sensitivity of all  blocks in the image is computed as shown in (5), where
blocks in the image is computed as shown in (5), where  is the number of
is the number of  blocks in the image:
blocks in the image:

Finally, points  and
and  are determined, in such a manner that these points never overlap or precede points
are determined, in such a manner that these points never overlap or precede points  or
or  . The point
. The point  is equal to the median of texture values that are between
is equal to the median of texture values that are between  and
and  values as shown in (6), where
values as shown in (6), where  is the Texture of
is the Texture of  th block and the point
th block and the point  is equal to the median of textures values that are between
is equal to the median of textures values that are between  and
and  values as shown in (7):
values as shown in (7):


When points  ,
,  ,
,  ,
,  , and
, and  are determined, the slopes of all membership functions (MFs) are computed. The membership function of the other dynamic parameter (Luminance sensitivity) is created in the same way. Membership functions for Luminance sensitivity and Location sensitivity are shown in Figure 3. It is worth mentioning that the shape of location sensitivity membership functions is different from the others, because the experiments showed that this kind of MFs better fits to the used data than the others. So, the location sensitivity membership function (
are determined, the slopes of all membership functions (MFs) are computed. The membership function of the other dynamic parameter (Luminance sensitivity) is created in the same way. Membership functions for Luminance sensitivity and Location sensitivity are shown in Figure 3. It is worth mentioning that the shape of location sensitivity membership functions is different from the others, because the experiments showed that this kind of MFs better fits to the used data than the others. So, the location sensitivity membership function ( ) is defined as the
) is defined as the  -function. The
-function. The  -function models this property using the following equation:
-function models this property using the following equation:

Figure 3(b) shows a plot of this function. In (8),  and
and  are two constant values that should be specified heuristically; for example, the best values that we found for not center curve were
are two constant values that should be specified heuristically; for example, the best values that we found for not center curve were  and
and  . The same curves for all images have been used.
. The same curves for all images have been used.
The membership functions for outputs of DFIS (α and β) are shown in Figure 4. After defuzzification we have crisp values for  and
and  which determine the suitability and weighting factor of
which determine the suitability and weighting factor of  th block of image. The blocks with highest
th block of image. The blocks with highest  values are selected for embedding process.
values are selected for embedding process.
2.2. Watermark Creation
As we know, most of the signal energy of the block DCT is compacted in the DC component and the remaining energy is distributed diminishingly in the AC components in zigzag scan order [4]. On the other hand, the DC component is more robust than AC components versus different attacks. However, with having only DC coefficient in each block of an image, the overall look of that image is presented. For example, Figure 5(b) shows the Lena image that created using only DC component of each  DCT block.
DCT block.
Since the DCT coefficients in one block for most images have a high correlation with the adjacent blocks; Gonzales et al. in [3] described a technique which estimates a few low-frequency AC coefficients precisely. Moreover, only the DC values of  neighborhoods of each central block are needed to estimate the AC coefficients of each central block as shown in Figure 6. The estimation relations for the first five AC coefficients of each
neighborhoods of each central block are needed to estimate the AC coefficients of each central block as shown in Figure 6. The estimation relations for the first five AC coefficients of each  DCT block are shown in Table 1 (first column) and Figure 5(c) shows the Lena image that created using these relations.
DCT block are shown in Table 1 (first column) and Figure 5(c) shows the Lena image that created using these relations.
 DCT block (1).
DCT block (1).Gonzales et al. [3] did not consider variations in the image in AC coefficients estimation, but in [4] a new method was proposed that considered the variation in the image and accordingly AC coefficients are estimated with different equations. This method is better than Gonzales method in terms of reduced blocking artifacts and improved PSNR value. In this method, at first, the entropy of each block is calculated and then blocks with entropy values less than a threshold value are defined as smoother blocks and blocks with entropy values equal or greater than a threshold are considered as featured blocks. Based on entropy values, three cases are considered in estimation relations: (1) Smoother blocks, (2) Featured blocks and (3) Featured blocks surrounded by featured blocks. The estimation formulas based on Veeraswamy method to support  DCT block for these three cases are shown in Table 1 (2th and 3th columns) and Table 2, correspondingly.
DCT block for these three cases are shown in Table 1 (2th and 3th columns) and Table 2, correspondingly.
 DCT block (2).
DCT block (2).Based on this idea, only DC coefficients are needed to estimate the AC coefficients of each block [4]. Therefore, the estimating formulas (as shown in Tables 1 and 2 for  DCT block) are employed to find these coefficients. Figure 5(d) shows a sample image that created by this method when the size of block is
DCT block) are employed to find these coefficients. Figure 5(d) shows a sample image that created by this method when the size of block is  .
.
For watermark creation process, as shown in Figure 7, the original grayscale watermark image is divided into  (e.g.,
(e.g.,  ) nonoverlapping blocks and subsequently performing the DCT on each block. Next, all AC coefficients are changed to zero.
) nonoverlapping blocks and subsequently performing the DCT on each block. Next, all AC coefficients are changed to zero.
In the proposed method, this created watermark image is inserted in the original image. In the extraction process, the estimating formulas (as shown in Tables 1 and 2 for  DCT block) are employed to reconstruct the watermark.
DCT block) are employed to reconstruct the watermark.
2.3. Watermark Insertion
To describe the proposed method, we supposed that the original image ( ) and created watermark image (
) and created watermark image ( ) are grayscale images with size
) are grayscale images with size  and
and  , respectively.
, respectively.
In the watermark embedding process, the original image is transformed to frequency domain by DCT. Because the JPEG standard is based on  block DCT, thus, block DCT with size of
block DCT, thus, block DCT with size of  is commonly used in image watermarking process to make it robust versus JPEG compression [29]. Based on this idea, the original image is divided into
is commonly used in image watermarking process to make it robust versus JPEG compression [29]. Based on this idea, the original image is divided into  nonoverlapping blocks and DCT is applied on each block. Next, the Dynamic Fuzzy Inference System (DFIS) is used to calculate the
nonoverlapping blocks and DCT is applied on each block. Next, the Dynamic Fuzzy Inference System (DFIS) is used to calculate the  and
and  for each
for each  DCT block of original image. Then, (
DCT block of original image. Then, ( ) number of blocks of original image with highest
) number of blocks of original image with highest  are selected for embedding watermark image, where
are selected for embedding watermark image, where  is the size of DCT block of watermark. In the other side, the image that is created by described approach in Section 2.2 (used watermark) is divided into
is the size of DCT block of watermark. In the other side, the image that is created by described approach in Section 2.2 (used watermark) is divided into  nonoverlapping blocks and then DCT is performed on each block. If
nonoverlapping blocks and then DCT is performed on each block. If  is smaller than
is smaller than  (in the proposed method, the value of
(in the proposed method, the value of  is 8), more robustness against attacks and more visual enhanced extracted watermark can be achieved but the quality of watermarked image is decreased. Thus,
is 8), more robustness against attacks and more visual enhanced extracted watermark can be achieved but the quality of watermarked image is decreased. Thus,  provides a tradeoff between robustness after attacks and quality of watermarked image. Finally, the DC value of each
provides a tradeoff between robustness after attacks and quality of watermarked image. Finally, the DC value of each  DCT block of the created watermark is embedded in DC value of each selected
DCT block of the created watermark is embedded in DC value of each selected  DCT block of original image (based on (9)). Therefore, the watermarked image is created by modifying DC value of each
DCT block of original image (based on (9)). Therefore, the watermarked image is created by modifying DC value of each  DCT block of the original image. As shown in Figure 8, the following steps are used to insert the watermark in the original image.
DCT block of the original image. As shown in Figure 8, the following steps are used to insert the watermark in the original image.
Algorithm 1 (The watermark embedding).
We have the following.
Input:
An original image  , watermark (
, watermark ( ).
).
Output:
A watermarked image  .
.
Step 1.
Divide the original image  , into
, into  nonoverlapping blocks and apply DCT on each block. Next, compute the HVS model properties as said in Section 2.1 and compute
nonoverlapping blocks and apply DCT on each block. Next, compute the HVS model properties as said in Section 2.1 and compute  and
and  values of each block with Fuzzy Inference System as described in Section 2.1. Finally, sort blocks in descending order of
values of each block with Fuzzy Inference System as described in Section 2.1. Finally, sort blocks in descending order of  value of each block.
value of each block.
Step 2.
Create used watermark ( ) from original watermark (
) from original watermark ( ) as described in Section 2.2.
) as described in Section 2.2.
Step 3.
Select first ( ) blocks of sorted blocks which is computed in Step 1 for embedding process (
) blocks of sorted blocks which is computed in Step 1 for embedding process ( is size of created watermark).
is size of created watermark).
Step 4.
Use (9) for invisible insertion of the created watermark (used watermark) into the DC coefficients of selected blocks of the original image:

where  and
and  are DC coefficients in
are DC coefficients in  th block of watermarked image and original image, respectively and
th block of watermarked image and original image, respectively and  is DC coefficient of
is DC coefficient of  th block in created watermark. The
th block in created watermark. The  parameter is a weighting factor that controls the tradeoff between invisibility, robustness, and detection fidelity of watermarked image which is computed by DFIS as described in Section 2.1. The
parameter is a weighting factor that controls the tradeoff between invisibility, robustness, and detection fidelity of watermarked image which is computed by DFIS as described in Section 2.1. The  parameter is a pseudorandom (1, −1) bit pattern that determines the addition or subtraction involved at each position which can be any arbitrarily chosen pseudorandom sequence. This parameter is just used for security purpose.
parameter is a pseudorandom (1, −1) bit pattern that determines the addition or subtraction involved at each position which can be any arbitrarily chosen pseudorandom sequence. This parameter is just used for security purpose.
Step 5.
Use inverse DCT on each  block to obtain watermarked image
block to obtain watermarked image  .
.
2.4. Watermark Extraction
The watermark extraction process is the reverse of embedding process and requires the original image. As illustrated in Figure 9, at first, the watermarked image ( ) and the original one (
) and the original one ( ) are divided into
) are divided into  nonoverlapping blocks and the DCT is performed on each block of images. Next, as described in Section 2.1,
nonoverlapping blocks and the DCT is performed on each block of images. Next, as described in Section 2.1,  and
and  values of each block in original image is computed with DFIS and then the (
values of each block in original image is computed with DFIS and then the ( ) number of blocks with highest
) number of blocks with highest  are selected (
are selected ( is number of
is number of  blocks in watermark image and
blocks in watermark image and  is size of it). Then, the DC coefficients of extracted watermark are computed as follows:
is size of it). Then, the DC coefficients of extracted watermark are computed as follows:

where  and
and  are DC coefficients of
are DC coefficients of  th block in watermarked image and original image, respectively and
th block in watermarked image and original image, respectively and  is DC coefficient of
is DC coefficient of  th block in extracted watermark. The
th block in extracted watermark. The  parameter is a weighting factor which is computed in Step 1 and the
parameter is a weighting factor which is computed in Step 1 and the  parameter is a pseudorandom (1, −1) bit pattern that generated with arbitrary seed and used in insertion process.
parameter is a pseudorandom (1, −1) bit pattern that generated with arbitrary seed and used in insertion process.
Finally, the  values and estimation formulas as described in Section 2.2 are used to create the
values and estimation formulas as described in Section 2.2 are used to create the  DCT blocks of watermark then by performing Block-wise inverse DCT, watermark in spatial domain is created. The following steps are used for watermark Extraction.
DCT blocks of watermark then by performing Block-wise inverse DCT, watermark in spatial domain is created. The following steps are used for watermark Extraction.
Algorithm 2 (The watermark extraction).
We have the following.
Input:
An original image ( ) and watermarked image (
) and watermarked image ( ).
).
Output:
An extracted watermark ( ).
).
Step 1.
Divide the original image into  nonoverlapping blocks and compute the DCT on each block. Then compute the HVS model properties as said in Section 2.1 and compute
nonoverlapping blocks and compute the DCT on each block. Then compute the HVS model properties as said in Section 2.1 and compute  and
and  values of each block with fuzzy approach (DFIS). Finally, sort blocks in descending order of
values of each block with fuzzy approach (DFIS). Finally, sort blocks in descending order of  value of each block.
value of each block.
Step 2.
Select first ( ) blocks of sorted blocks which is computed in Step 1 for extracting process.
) blocks of sorted blocks which is computed in Step 1 for extracting process.  is number of
is number of  blocks in watermark and
blocks in watermark and  is size of watermark.
is size of watermark.
Step 3.
Divide the watermarked image  into
into  nonoverlapping blocks and compute the DCT on each block.
nonoverlapping blocks and compute the DCT on each block.
Step 4.
Extract the watermark from selected blocks use (10).
Step 5.
Estimate AC coefficients of each block in extracted watermark from Step 4, then use  Block-wise inverse DCT to create extracted watermark in spatial domain (
Block-wise inverse DCT to create extracted watermark in spatial domain ( ). If the input watermark image is present in the extracted image, then the ownership is approved.
). If the input watermark image is present in the extracted image, then the ownership is approved.
3. Structural Comparison of Proposed Method with Related Ones
The employed techniques in proposed method make it more robust and its results with more quality. In this section, the differences and excellences of proposed method with two related methods [24, 27] are introduced in four conventional different steps of watermarking methods: (1) selecting embedding area procedure, (2) watermark creation procedure, (3) inserting procedure, (4) extracting procedure. Also, the motivation of proposed method is implied in subsections.
3.1. Selecting Embedding Area Procedure
Mohanty's method [24], at first, finds the most perceptually important subimage of original image, where the size of subimage is equal to size of watermark ( ) to embed the watermark in it. To find this subimage, the properties of Human Visual System (HVS) such as Luminance, Edginess, Contrast, Location and Texture are calculated for each
) to embed the watermark in it. To find this subimage, the properties of Human Visual System (HVS) such as Luminance, Edginess, Contrast, Location and Texture are calculated for each  subimage of original image and the high score one is selected as most perceptually important region of original image and watermark is embedded in it. As result, this method is not robust to geometrical attacks such as Tampering, Data block removal and Cropping; because the watermark is embedded in consecutive blocks (subimage) of original image. For example if this region of watermarked image is cropped or tampered, the whole watermark is removed and the extraction procedure cannot find any watermark in the test image (see Section 4.3). But, in the proposed method, blocks of the watermark are not embedded in consecutive blocks of original image and embedded in nonconsecutive blocks of original image. As result, the proposed method is more robust versus many geometrical attacks such as Tampering, Data block removal, and Cropping (see Sections 4.2 and 4.3).
subimage of original image and the high score one is selected as most perceptually important region of original image and watermark is embedded in it. As result, this method is not robust to geometrical attacks such as Tampering, Data block removal and Cropping; because the watermark is embedded in consecutive blocks (subimage) of original image. For example if this region of watermarked image is cropped or tampered, the whole watermark is removed and the extraction procedure cannot find any watermark in the test image (see Section 4.3). But, in the proposed method, blocks of the watermark are not embedded in consecutive blocks of original image and embedded in nonconsecutive blocks of original image. As result, the proposed method is more robust versus many geometrical attacks such as Tampering, Data block removal, and Cropping (see Sections 4.2 and 4.3).
In Asatryan's method [27] that inserts the watermark in spatial domain, all pixels of original image are used to embed the watermark. Therefore, the quality of watermarked image in this method is degraded and artifact is produced in watermarked image (see Section 4.3).
3.2. Watermark Creation Procedure
Mohanty's method create synthetic image by using  DCT coefficients of selected subimage of original image and Gaussian, Laplacian distributions for DC, AC coefficients, respectively. Then, the original watermark is embedded in the created synthetic image using any DCT-based visible watermarking algorithm to create used watermark.
DCT coefficients of selected subimage of original image and Gaussian, Laplacian distributions for DC, AC coefficients, respectively. Then, the original watermark is embedded in the created synthetic image using any DCT-based visible watermarking algorithm to create used watermark.
In the Asatryan's method, the used watermark is created by compressing the original watermark that the rate of compression is defined by user.
In the proposed method the used watermark is created by dividing the original watermark into  DCT blocks and changing the AC coefficients of each block to zero. The
DCT blocks and changing the AC coefficients of each block to zero. The  parameter provides a tradeoff between quality of watermarked image and extracted watermark. The proposed creation watermark procedure is acceptable because the watermark image that creates by only DC coefficients of each
parameter provides a tradeoff between quality of watermarked image and extracted watermark. The proposed creation watermark procedure is acceptable because the watermark image that creates by only DC coefficients of each  (where
(where  ; e.g.,
; e.g.,  ) DCT block of original watermark is perceptually similar as original one. Also, the AC coefficients estimating formulas that propose in [4] can be used to increase the quality of created watermark.
) DCT block of original watermark is perceptually similar as original one. Also, the AC coefficients estimating formulas that propose in [4] can be used to increase the quality of created watermark.
3.3. Inserting Procedure
In the Mohanty's method the used watermark is embedded into the original image by fusing the DCT coefficients of used watermark blocks with the corresponding blocks of the selected subimage. In the other hand, the DCT coefficients of each  DCT block of used watermark is embedded in corresponding
DCT block of used watermark is embedded in corresponding  DCT block of selected subimage. As result, the robustness of mohanty's method decreases because the AC coefficients of DCT block is not robust to many attacks such as Low Pass Filtering, Compression, Median Filtering. Therefore, the many of embedded AC coefficients of used watermark are degraded after such attacks. To solve this drawback, in the proposed method, the coefficients of
DCT block of selected subimage. As result, the robustness of mohanty's method decreases because the AC coefficients of DCT block is not robust to many attacks such as Low Pass Filtering, Compression, Median Filtering. Therefore, the many of embedded AC coefficients of used watermark are degraded after such attacks. To solve this drawback, in the proposed method, the coefficients of  (where
(where  ) DCT blocks of used watermark are embedded only in DC coefficients of each
) DCT blocks of used watermark are embedded only in DC coefficients of each  DCT block of original image. As result, the robustness of proposed method is higher than mohanty's method,because the DC coefficients of DCT block is robust than AC coefficients of one.
DCT block of original image. As result, the robustness of proposed method is higher than mohanty's method,because the DC coefficients of DCT block is robust than AC coefficients of one.
The Asatryan's method works in spatial domain to embed the watermark in original image. In this method, the values of  block DCT coefficients of compressed watermark are mapped to the interval [0,255] by fixed linear transform and the mapped values of DCT coefficients are embedded in pixel values of each block of original image. As result, because the embedding is done in special domain, the robustness of this method is decreased and the quality of watermarked image is low (see Section 4.3). Also, mapping the DCT coefficients to the interval [0,255] may be caused distortion in the extracted watermark.
block DCT coefficients of compressed watermark are mapped to the interval [0,255] by fixed linear transform and the mapped values of DCT coefficients are embedded in pixel values of each block of original image. As result, because the embedding is done in special domain, the robustness of this method is decreased and the quality of watermarked image is low (see Section 4.3). Also, mapping the DCT coefficients to the interval [0,255] may be caused distortion in the extracted watermark.
The weighted factor (β) is used in all three methods. The value of this parameter is 0.02 for DC and 0.1 for AC coefficients in Mohanty's method and 0.07 for all pixels in Asatryan's method. But, in the proposed method, the value of this parameter for each DCT block is based on Texture and Luminance of this block. It is based on idea that modification inside a highlytextured block is unnoticeable to the human eye and the brighter the background is the lower the visibility of the embedded watermark. Therefore, the proposed method produces a watermarked image with higher quality than two related methods.
3.4. Extracting Procedure
The Mohanty's method use a reverse embedding procedure to extract the DCT coefficients of each  DCT block of watermark and applied IDCT to create watermark in spatial domain. But in proposed method a reverse embedding procedure is performed to extract the only DC coefficients of each
DCT block of watermark and applied IDCT to create watermark in spatial domain. But in proposed method a reverse embedding procedure is performed to extract the only DC coefficients of each  DCT block of watermark. Then the estimation formulas are used to evaluate the AC coefficients of each
DCT block of watermark. Then the estimation formulas are used to evaluate the AC coefficients of each  DCT block (e.g., first five AC coefficients when
DCT block (e.g., first five AC coefficients when  ) of watermark and applied IDCT to create watermark in spatial domain.
) of watermark and applied IDCT to create watermark in spatial domain.
The Asatryan's method use a reverse embedding procedure (in spatial domain) to extract the mapped DCT coefficients of watermark. Then the reverse of linear transform that used in embedding process is used to create the DCT coefficients of watermark. Finally, IDCT is applied to create the watermark in spatial domain. The steps of Mohanty's method, Asatryan' method and proposed watermarking method are summarized in Table 3.
4. Experimental Results
The proposed algorithm has been tested on different images and a big set of grayscale watermark images but only results for four popular images and two logos with different sizes are presented here. The selected logos are Texas University and ShahidBeheshti University ones. We have chosen Lena, Baboon, Peppers and Crowd grayscale images with size  as shown in Figure 10 to embed watermarks in them and the watermarks are grayscale watermark logos with size
as shown in Figure 10 to embed watermarks in them and the watermarks are grayscale watermark logos with size  and
and  as shown in Figure 11. Also, based on experiments on different watermark images (with size
as shown in Figure 11. Also, based on experiments on different watermark images (with size  and
and  ), the value of
), the value of  was selected equal to 4. The program development tool was MATLAB and the computation platform was a personal computer with 1.66 GHZ of CPU and 2 GB of RAM.
was selected equal to 4. The program development tool was MATLAB and the computation platform was a personal computer with 1.66 GHZ of CPU and 2 GB of RAM.
The experiments confirmed the effectiveness of the proposed algorithm in producing visually pleasing watermarked images and in addition the extracted watermark was visually recognizable and similar to both inserted watermark and original watermark. Our scheme requires one key as seed of random number generator to be stored for extraction phase, so this method has no storage overhead. After the watermark is embedded into the original image, the PSNR (Peak Signal to Noise Ratio) is used to evaluate thequality of the watermarked image. The MSE and PSNR values in decibels (dB) are defined as follows:

where  represents the
represents the  pixel value of original image and
pixel value of original image and  represents the
represents the  pixel value of watermarked image. The other metric used to test the quality of the retrieved watermark image is Normalized Cross Correlation (NCC). It is defined as follows:
pixel value of watermarked image. The other metric used to test the quality of the retrieved watermark image is Normalized Cross Correlation (NCC). It is defined as follows:

where  and
and  are extracted watermark and inserted watermark images, respectively, and
are extracted watermark and inserted watermark images, respectively, and  and
and  are their pixels mean values, respectively. The subscripts
are their pixels mean values, respectively. The subscripts  ,
,  of
of  or
or  denote the index of an individual pixel of the corresponding image. The summations are over all the image pixels.
denote the index of an individual pixel of the corresponding image. The summations are over all the image pixels.
The other part of experiments involved testing the algorithm against many common attacks on watermarked image and fortunately the extracted watermark in almost cases was detectable and acceptable due to the original and inserted watermark. In these experiments, we used StirMarkMATLAB software that contains approximately 90 different types of image manipulations. But, in the following subsections, we will present only the experimental results for test images, and nongeometric and geometric attacks such as Compression, Noise addition, Filtering, Cropping, Changing Aspect Ratio, Tampering and Scaling on the watermarked images to evaluate the robustness of the proposed scheme.
4.1. Quality of Watermarked Image and Extracted Watermark before Attack
Four selected images that used in embedding processare shown in Figure 10. Also, we used two watermarks in Figure 11 at two sizes ( and
and  ) to be embedded in these original images. The watermarked images and the extracted watermarks with corresponding PSNR with different size of watermarks (
) to be embedded in these original images. The watermarked images and the extracted watermarks with corresponding PSNR with different size of watermarks ( and
and  ) are shown in Figures 12 and 13, respectively.
) are shown in Figures 12 and 13, respectively.
(a)–(d) Watermarked images after embedding 128 × 128 watermark image as shown in Figure 11(b). (e)–(h) Extracted watermarks from (a)–(d), respectively. (i)–(l) Watermarked images after embedding 128 × 128 watermark image as shown in Figure 11(d). (m)–(p) Extracted watermarks from (i)–(l), respectively. (a)PSNR: 52.33 dB (b)PSNR: 52.44 dB (c)PSNR: 51.72 dB (d)PSNR: 51.38 dB (e)γ = 0.9974 (f)γ = 0.9973 (g)γ = 0.9979 (h)γ = 0.9974 (i)PSNR: 52.92 dB (j)PSNR: 53.08 dB (k)PSNR: 52.27 dB (l)PSNR: 52.04 dB (m)γ = 0.9975 (n)γ = 0.9970 (o)γ = 0.9982 (p)γ = 0.9971
(a)–(d) Watermarked images after embedding 256 × 256 watermark image as shown in Figure 11(b). (e)–(h) Extracted watermarks from (a)–(d), respectively. (i)–(l) Watermarked images after embedding 256 × 256 watermark image as shown in Figure 11(d). (m)–(p) Extracted watermarks from (i)–(l), respectively. (a)PSNR: 48.27 dB (b)PSNR: 48.47 dB (c)PSNR: 47.94 dB (d)PSNR: 47.63 dB (e)γ = 0.9975 (f)γ = 0.9966 (g)γ = 0.9971 (h)γ = 0.9965 (i)PSNR: 48.84 dB (j)PSNR: 49.11 dB (k)PSNR: 48.66 dB (l)PSNR: 48.26 dB (m)γ = 0.9972 (n)γ = 0.9967 (o)γ = 0.9969 (p)γ = 0.9963
It is obvious that the PSNR value of the watermarked image had a higher value in comparison with other existing watermarking algorithms. The average PSNR value for the watermarked images was approximately 52 dB, where the size of watermark images is  . Also, the average PSNR value for the watermarked images was approximately 49 dB, where the size of watermark images is
. Also, the average PSNR value for the watermarked images was approximately 49 dB, where the size of watermark images is  . So, the watermark embedding process produced high-quality watermarked images.
. So, the watermark embedding process produced high-quality watermarked images.
4.2. Quality of Watermarked Image and Extracted Watermark versus Various Attacks
In the following experiment, we used several image manipulations, including Compression, Noise addition, Filtering, Cropping, Changing aspect ratio, Tampering, Copy attack, Scaling and Composite attacks on the watermarked images to evaluate the robustness of the proposed scheme.
4.2.1. Compression
JPEG Compression
Using image compression before storing and transmitting images is very common. JPEG from Joint Photographic Experts Group has been funded its way through digital imaging and is very popular image compression tool for still images. So we evaluated the robustness of the proposed scheme by compressing the watermarked images with different JPEG quality factors. Figures 14(a)–14(d), 14(i)–14(l) show the watermarked images with watermark size  after JPEG compression with quality factor 40%, 30%, 20% and 10% for Lena, Baboon, Peppers and Crowd images, respectively. Figures 14(e)–14(h), 14(m)–14(p) show the extracted watermark from Figures 14(a)–14(d), 14(i)–14(l), respectively. Also, Figures 15(a)–15(d), 15(i)–15(l) show the watermarked images with watermark size
after JPEG compression with quality factor 40%, 30%, 20% and 10% for Lena, Baboon, Peppers and Crowd images, respectively. Figures 14(e)–14(h), 14(m)–14(p) show the extracted watermark from Figures 14(a)–14(d), 14(i)–14(l), respectively. Also, Figures 15(a)–15(d), 15(i)–15(l) show the watermarked images with watermark size  after JPEG compression with quality factor 40%, 30%, 20% and 10% for Lena, Baboon, Peppers and Crowd images, respectively and Figures 15(e)–15(h), 15(m)–15(p) show the extracted watermark from Figures 15(a)–15(d), 15(i)–15(l), respectively. The results show that the proposed scheme is robust against JPEG image compression and the extracted watermarks are visually similar to inserted watermark under different quality factors of JEPG compression.
after JPEG compression with quality factor 40%, 30%, 20% and 10% for Lena, Baboon, Peppers and Crowd images, respectively and Figures 15(e)–15(h), 15(m)–15(p) show the extracted watermark from Figures 15(a)–15(d), 15(i)–15(l), respectively. The results show that the proposed scheme is robust against JPEG image compression and the extracted watermarks are visually similar to inserted watermark under different quality factors of JEPG compression.
(a)–(d) The watermarked Lena, Baboon, Peppers and Crowd images with 256 × 256 watermark image as shown in Figure 11(b) after JPEG compression with quality factor 40%, 30%, 20% and 10%, respectively. (e)–(h) The extracted watermarks (256 × 256) from (a)–(d), respectively. (i)–(l) The watermarked Lena, Baboon, Peppers and Crowd images with 256 × 256 watermark image as shown in Figure 11(d) after JPEG compression with quality factor 40%, 30%, 20% and 10%, respectively. (m)–(p) The extracted watermarks (256 × 256) from (i)–(l), respectively. (a)PSNR = 34.89 dB (b)PSNR = 31.71 dB (c)PSNR = 32.32 dB (d)PSNR = 27.72 dB (e)γ = 0.7689 (f)γ = 0.7120 (g)γ = 0.5794 (h)γ = 0.4493 (i)PSNR = 34.91 dB (j)PSNR = 31.73 dB (k)PSNR = 32.35 dB (l)PSNR = 27.72 dB (m)γ = 0.8319 (e)γ = 0.7029 (o)γ = 0.5629 (p)γ = 0.4065
(a)–(d) The watermarked Lena, Baboon, Peppers and Crowd images with 128 × 128 watermark image as shown in Figure 11(b) after JPEG compression with quality factor 40%, 30%, 20% and 10%, respectively. (e)–(h) The extracted watermarks (128 × 128) from (a)–(d), respectively. (i)–(l) The watermarked Lena, Baboon, Peppers and Crowd image with 128 × 128 watermark images as shown in Figure 11(d) after JPEG compression with quality factor 40%, 30%, 20% and 10%, respectively. (m)–(p) The extracted watermarks (128 × 128) from (i)–(l), respectively. (a)PSNR = 35.04 dB (b)PSNR = 31.78 dB (c)PSNR = 32.41 dB (d)PSNR = 27.74 dB (e)γ = 0.9974 (f)γ = 0.8090 (g)γ = 0.7755 (h)γ = 0.6239 (i)PSNR = 35.05 dB (j)PSNR = 31.79 dB (k)PSNR = 32.42 dB (l)PSNR = 27.75 dB (m)γ = 0.8673 (n)γ = 0.7774 (o)γ = 0.7275 (p)γ = 0.5601
Wavelet Compression (JPEG2000)
We evaluated the robustness of proposed method against another version of compression that is wavelet compression. Figures 16(a)–16(d) show the results of applying wavelet compression on Lena, Baboon, Peppers and crowd images with compression ratio 0.4 bpp, 0.8 bpp, 1.5 bpp and 3.5 bpp, respectively. The extracted watermarks that shown in Figures 16(e)–16(h) are still visually detectable after this attack.
(a)–(d) The watermarked Lena, Baboon, Peppers and Crowd images with 256 × 256 watermark image after wavelet compression with quality factor 0. 4 bpp, 0.8 bpp, 1.5 bpp and 3.5 bpp, respectively. (e)–(h) The extracted watermarks (256 × 256) from (a)–(d), respectively. (a)PSNR = 35.22 dB (b)PSNR = 33.93 dB (c)PSNR = 38.17 dB (d)PSNR = 47.02 dB (e)γ = 0.5387 (f)γ = 0.7754 (g)γ = 0.9579 (h)γ = 0.9957
4.2.2. Noise Addition
The robustness of proposed method has been evaluated by adding Gaussian noise with mean = 0 and variance = 0.002 on the watermarked images. Figures 17(a)–17(d), 17(i)–17(l) show the results of adding Gaussian noise. The extracted watermarks are still visually detectable after this attack (as shown in Figures 17(e)–17(h), 17(m)–17(p). It indicates that the proposed scheme is also robust to noise attack.
(a) and (b) Lena and Peppers watermarked imageswith 256 × 256 watermark image as shown in Figure 11(b) after adding Gaussian noise with mean = 0 and variance = 0.002, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after adding Gaussian noise. (g) and (h) The extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after adding Gaussian noise, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after adding Gaussian noise. (o) and (p) The extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 26.95 dB (b)PSNR = 27.08 dB (c)PSNR = 27.08 dB (d)PSNR = 26.96 dB (e)γ = 0.6630 (f)γ = 0.6474 (g)γ = 0.7975 (h)γ = 0.7497 (i)PSNR = 26.98 dB (j)PSNR = 27.08 dB (k)PSNR = 27.07 dB (l)PSNR = 26.94 dB (m)γ = 0.7032 (n)γ = 0.7643 (o)γ = 0.6143 (p)γ = 0.6070
4.2.3. Filtering
The robustness of watermarking scheme has been also tested by performing various filters such as sharpening, Gaussian lowpass filter, averaging, median, and blurring on the watermarked images. Figures 18(a)–18(d), 18(i)–18(l) show the resultant images after performing Gaussian lowpass filter with window size  . Figures 18(e)–18(h), 18(m)–18(p) show the extracted watermarks and corresponding
. Figures 18(e)–18(h), 18(m)–18(p) show the extracted watermarks and corresponding  values. The extracted watermarks are still visually detectable after this attack. It indicates that the proposed scheme is also robust to Gaussian lowpass filter attack.
values. The extracted watermarks are still visually detectable after this attack. It indicates that the proposed scheme is also robust to Gaussian lowpass filter attack.
(a) and (b) The Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after performing Gaussian lowpass filter with window size 5 × 5, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after performing Gaussian lowpass filter, (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after performing Gaussian lowpass filter, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after performing Gaussian lowpass filter, (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 33.25 dB (b)PSNR = 32.28 dB (c)PSNR = 30.11 dB (d)PSNR = 28.67 dB (e)γ = 0.8948 (f)γ = 0.8994 (g)γ = 0.7074 (h)γ = 0.7940 (i)PSNR = 33.33 dB (j)PSNR = 32.34 dB (k)PSNR = 30.07 dB (l)PSNR = 28.64 dB (m)γ = 0.8646 (n)γ = 0.8598 (o)γ = 0.6502 (p)γ = 0.7751
Figures 19(a)–19(d), 19(i)–19(l) show the resultant images by averaging filter with window size  . Figures 19(e)–19(h), 19(m)–19(p) show the extracted watermarks and their
. Figures 19(e)–19(h), 19(m)–19(p) show the extracted watermarks and their  values. The extracted watermarksare still visually detectable after averaging filter attack.
values. The extracted watermarksare still visually detectable after averaging filter attack.
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after performing Average filter with window size 5 × 5, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after performing Average filter, (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after performing Average filter, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after performing Average filter, (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 29.60 dB (b)PSNR = 29.08 dB (c)PSNR = 25.31 dB (d)PSNR = 24.34 dB (e)γ = 0.8577 (f)γ = 0.8621 (g)γ = 0.6194 (h)γ = 0.7174 (i)PSNR = 29.63 dB (j)PSNR = 29.11 dB (k)PSNR = 25.30 dB (l)PSNR = 24.33 dB (m)γ = 0.8172 (n)γ = 0.8074 (o)γ = 0.5654 (p)γ = 0.6998
Figures 20(a)–20(d), 20(i)–20(l) show the resultant images after blurring with radius 3. Figures 20(e)–20(h), 20(m)–20(p) show the extracted watermarks and their  values. The extracted watermarks are still visually detectable after this attack. It indicates that the proposed scheme is also robust to blurring attack.
values. The extracted watermarks are still visually detectable after this attack. It indicates that the proposed scheme is also robust to blurring attack.
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after Bluring with radius 3, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after Bluring, (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after Bluring, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after Bluring, (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 29.12 dB (b)PSNR = 28.81 dB (c)PSNR = 24.66 dB (d)PSNR = 23.89 dB (e)γ = 0.9407 (f)γ = 0.9404 (g)γ = 0.8287 (h)γ = 0.8830 (i)PSNR = 29.14 dB (j)PSNR = 28.83 dB (k)PSNR = 24.65 dB (l)PSNR = 23.88 dB (m)γ = 0.9191 (n)γ = 0.9215 (o)γ = 0.7743 (p)γ = 0.8701
Figures 21(a)–21(d), 21(i)–21(l) show the resultant images by sharpening. Figures 21(e)–21(h), 21(m)–21(p) show the extracted watermarks. Also, Figures 22(a)–22(d), 22(i)–22(l) show the resultant images after median filtering with window size  . Figures 22(e)–22(h), 22(m)–22(p) show the extracted watermarks and their
. Figures 22(e)–22(h), 22(m)–22(p) show the extracted watermarks and their  values. The test results show that the watermark image can also detectable after the filter attacks. (it is worth mentioning that because we zoomed out images in the paper the effects of some filters are not visible in these sizes).
values. The test results show that the watermark image can also detectable after the filter attacks. (it is worth mentioning that because we zoomed out images in the paper the effects of some filters are not visible in these sizes).
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after Sharpening, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after Sharpening, (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after Sharpening, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after Sharpening, (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 25.34 dB (b)PSNR = 25.15 dB (c)PSNR = 23.28 dB (d)PSNR = 21.10 dB (e)γ = 0.7308 (f)γ = 0.7144 (g)γ = 0.6174 (h)γ = 0.5034 (i)PSNR = 25.39 dB (j)PSNR = 25.20 dB (k)PSNR = 23.27 dB (l)PSNR = 21.08 dB (m)γ = 0.6679 (n)γ = 0.6684 (o)γ = 0.3421 (p)γ = 0.4626
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after applying Median filter with window size 5 × 5, (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after appling Median filter, (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after appling Median filter, (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after appling Median filter, (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 31.17 dB (b)PSNR = 32.08 dB (c)PSNR = 26.46 dB (d)PSNR = 24.60 dB (e)γ = 0.8768 (f)γ = 0.8818 (g)γ = 0.6537 (h)γ = 0.5993 (i)PSNR = 31.22 dB (j)PSNR = 32.14 dB (k)PSNR = 26.48 dB (l)PSNR = 24.59 dB (m)γ = 0.8426 (n)γ = 0.8476 (o)γ = 0.6247 (p)γ = 0.6046
4.2.4. Geometric Attacks
In the following experiments, different geometric attacks such as scaling, cropping, tampering and changing aspect ratio are performed on the watermarked images to test the robustness of proposed method.
Scaling
In this experimental the watermarked images are reduced to 1/2 and 1/4 of its original size. In order to detect the watermark, the reduced images are recovered to its original dimension, respectively. Figures 23(a)–23(d), 23(i)–23(l) show the watermarked image after reducing to 1/2 and recovering to original dimension. Figures 23(e)–23(h), 23(m)–23(p) show the extracted watermark from Figures 23(a)–23(d), 23(i)–23(l), respectively.
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after Scaling (1/2), (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after Scaling (1/2), (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after Scaling (1/2), (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after Scaling (1/2), (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 33.94 dB (b)PSNR = 31.85 dB (c)PSNR = 31.85 dB (d)PSNR = 29.29 dB (e)γ = 0.9528 (f)γ = 0.9402 (g)γ = 0.8835 (h)γ = 0.8860 (i)PSNR = 34.06 dB (j)PSNR = 31.93 dB (k)PSNR = 31.79 dB (l)PSNR = 29.26 dB (m)γ = 0.9462 (n)γ = 0.9142 (o)γ = 0.8651 (p)γ = 0.8702
Figures 24(a)–24(d), 24(i)–24(l) show the watermarked image after reducing to 1/4 and recovering to original dimension. Figures 24(e)–24(h), 24(m)–24(p) show the extracted watermark from Figures 24(a)–24(d), 24(i)–24(l) and corresponding  values, respectively. The test results show that the watermark image can also detectable after the scaling attacks.
values, respectively. The test results show that the watermark image can also detectable after the scaling attacks.
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b) after Scaling (1/4), (e) and (f) the extracted watermarks with size 256 × 256 from (a) and (b), respectively. (c) and (d) Crowd and Baboon watermarked images with 128 × 128 watermark image as shown in Figure 11(b) after Scaling (1/4), (g) and (h) the extracted watermarks with size 128 × 128 from (c) and (d), respectively. (i) and (j) Lena and Peppers watermarked images with 128 × 128 watermark image as shown in Figure 11(d) after Scaling (1/4), (m) and (n) the extracted watermarks with size 128 × 128 from (i) and (j), respectively. (k) and (l) Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d) after Scaling (1/4), (o) and (p) the extracted watermarks with size 256 × 256 from (k) and (l), respectively. (a)PSNR = 28.80 dB (b)PSNR = 28.00 dB (c)PSNR = 24.00 dB (d)PSNR = 23.58 dB (e)γ = 0.7144 (f)γ = 0.6931 (g)γ = 0.6285 (h)γ = 0.4076 (i)PSNR = 28.83 dB (j)PSNR = 28.02 dB (k)PSNR = 23.99 dB (l)PSNR = 23.57 dB (m)γ = 0.6494 (n)γ = 0.6022 (o)γ = 0.3308 (p)γ = 0.4237
Cropping
In this experimental the watermarked images are cropped. Figures 25(a)–25(d) show the cropped version of Lena, Baboon, Peppers and Crowd watermarked image respectively. Figures 25(e)–25(h) show the extracted watermark from these figures. As shown from these figures, the extracted watermarks are visually detectable yet.
Changing Aspect Ratio
In this experiment, the robustness of proposed method was tested by changing aspect ratio of watermarked image. Figures 26(a) and 26(b) show the Lena and Peppers images after changing aspect ratio ( ,
,  ) of these images and Figures 26(c) and 26(d) show the Baboon and Crowd images after changing aspect ratio (
) of these images and Figures 26(c) and 26(d) show the Baboon and Crowd images after changing aspect ratio ( ,
,  ) of these images. To extract the watermark, the images were rescaled to original size (
) of these images. To extract the watermark, the images were rescaled to original size ( ) and the extracted watermarks from these figures are shown in Figures 26(e)–26(h).
) and the extracted watermarks from these figures are shown in Figures 26(e)–26(h).
(a) and (b) The watermarked Lena and Peppers images after changing aspect ratio attack (X =1, Y = 1.2), respectively. (c) and (d) the watermarked Baboon and Crowd images after changing aspect ratio attack (X = 0.8, Y = 1), respectively. (e)–(h) The extracted watermarks from (a)–(d), respectively. (a)PSNR = 27.50 dB (b)PSNR = 26.49 dB (c)PSNR = 24.45 dB (d)PSNR = 26.36 dB (e)γ = 0.6733 (f)γ = 0.5809 (g)γ = 0.6440 (h)γ = 0.5666
Tampering and Data Blocks Removal
We tested the robustness of proposed method by tampering the watermarked images. Figures 27(a)–27(d) show the results of tampering Lena, Baboon, Peppers and Crowd images, respectively. As shown in Figures 27(e)–27(h), the extracted watermarks are still visually detectable after this attack and it indicates that the proposed scheme is also robust to such attacks. Also, Figures 27(i)–27(l) show the results of data blocks removing of Lena, Baboon, Peppers and Crowd images, respectively and Figures 27(m)–27(p) show the extracted watermark from Figures 27(i)–27(l), respectively. As result, the extracted watermark after such attacks are still visually detectable and the proposed method is robust to tampering and data blocks removal.
(a)–(d) The watermarked Lena, Baboon, Peppers and Crowd images after tampering, respectively. (e)–(h) The extracted watermarks from (a)–(d), respectively. (i)–(l) The watermarked Lena, Baboon, Peppers and Crowd images after data blocks removal, respectively. (m)–(p) The extracted watermarks from (i)–(l), respectively. (a)PSNR = 15.35 dB (b)PSNR = 19.59 dB (c)PSNR = 16.37 dB (d)PSNR = 18.46 dB (e)γ = 0.7167 (f)γ = 0.9090 (g)γ = 0.7598 (h)γ = 0.8415 (i)PSNR = 15.33 dB (j)PSNR = 14.49 dB (k)PSNR = 15.87 dB (l)PSNR = 14.63 dB (m)γ = 0.7698 (n)γ = 0.7702 (o)γ = 0.7816 (p)γ = 0.6724
Copy Attack
The copy attack has been used to create the false positive problem and operated as follow: (1) a watermark is first predicted from watermarked image, (2) the predicted watermark into a target image to create counterfeit watermarked image, (3) from the counterfeit image, a watermark can be detected that wrongly claims rightful ownership.
In this experiment, the robustness of proposed watermarking method was tested by applying copy attack on watermarked image. Figures 28(a) and 28(b) show the Lena and Peppers watermarked imageswith  watermark image as shown in Figure 11(b) and Figures 28(c) and 28(d) show the Lena and Peppers watermarked imageswith
watermark image as shown in Figure 11(b) and Figures 28(c) and 28(d) show the Lena and Peppers watermarked imageswith  watermark image as shown in Figure 11(d). Figures 28(e)–28(h) show the counterfeit watermarked image with Figures 28(a)–28(d), respectively. The extracting watermarks from Figures 28(e)–28(h) are shown in Figures 28(i)–28(l), respectively. Therefore, the proposed method is robust against copy attack.
watermark image as shown in Figure 11(d). Figures 28(e)–28(h) show the counterfeit watermarked image with Figures 28(a)–28(d), respectively. The extracting watermarks from Figures 28(e)–28(h) are shown in Figures 28(i)–28(l), respectively. Therefore, the proposed method is robust against copy attack.
(a) and (b) Lena and Peppers watermarked images with 256 × 256 watermark image as shown in Figure 11(b), (e) and (f) the counterfeit watermarked image with (a) and (b), respectively. (c) and (d) The Crowd and Baboon watermarked images with 256 × 256 watermark image as shown in Figure 11(d), (g) and (h) the counterfeit watermarked image with (c) and (d), respectively. (i)–(l) the extracted watermark from (e)–(h), respectively. (a)PSNR = 48.27 dB (b)PSNR = 48.47 dB (c)PSNR = 48.66 dB (d)PSNR = 48.26 dB (e) (f) (g) (h) (i)γ = -0.0145 (j)γ = -0.1253 (k)γ = -0.0246 (l)γ = -0.0057
4.2.5. Composite Attacks
The purpose of this experiment is to check whether this kind of combination attack is able to remove the watermark of the proposed method. Figures 29(a)–29(h) show the watermarked images after different composite attacks and Figures 29(i)–29(p) show the extracted watermarks from Figures 29(a)–29(h), respectively.
(a)–(h) The watermarked image after different composite attacks, (i)–(k) The extracted watermark from (a)–(h), respectively. (a)PSNR = 31.17 dB Wiener filter (3 × 3) + Scaling (1/2) + JPEG(80) (b)PSNR = 27.08 dB Softthreshold + Blurring (1) + JPEG(85) (c)PSNR = 24.46 dB Hardthreshold + Averagefiltr (3 × 3) + JPEG(80) (d)PSNR = 24.60 dB Templateremoval + Scalin (1/2) + JPEG(85) (e)PSNR = 31.22 dB Blurring (2) + JPEG(80) (f)PSNR = 32.14 dB Median filter (3 × 3) + JPEG(85) (g)PSNR = 26.48 dB Sharpening (1) + JPEG(90) (f)PSNR = 24.59 dB Blurring (2) + JPEG(80) (i)γ = 0.8768 (j)γ = 0.7999 (k)γ = 0.7472 (l)γ = 0.7472 (m)γ = 0.6889 (n)γ = 0.7560 (o)γ = 0.7983 (p)γ = 0.4247 (p)γ = 0.8098
Therefore, the experimental results presented on the quality and recognize ability demonstrates the performance of our method under various attacks.
4.3. Comparison with Other Related Methods
In this subsection, the results of proposed method are compared with two related ones which have been presented by Mahanty and Bhargava [24] and D. Asatryan and N. Asatryan [27]. The comparison is based on four metrics: (1) average execution time for watermark insertion (2) PSNR value of watermarked image, (3) PSNR or correlation value ( ) value of extracted watermark and (4) error rate of detecting watermark.
) value of extracted watermark and (4) error rate of detecting watermark.
These three methods were implemented on a personal computer with 1.66 GHZ of CPU and 2 GB of RAM and the average execution time of proposed method for watermark insertion was approximately 2 sec for an image with size 512 × 512 pixels and watermark image with size  pixels. The execution time for Mohanty method was 4 sec that is approximately 50% higher in time than proposed algorithm and 1 sec for Asatryan method that is approximately 50% lower than proposed algorithm.
pixels. The execution time for Mohanty method was 4 sec that is approximately 50% higher in time than proposed algorithm and 1 sec for Asatryan method that is approximately 50% lower than proposed algorithm.
Based on experiments, in the proposed method, the average minimum value of  was 0.4 when the extracted watermark was visually detectable. This value for Mohanty method and Asatryan method were 0.65 and 0.3, respectively.
was 0.4 when the extracted watermark was visually detectable. This value for Mohanty method and Asatryan method were 0.65 and 0.3, respectively.
To have a complete comparison between proposed method and related ones, we embedded the 50 different watermark images in three sizes ( ,
,  and
and  ) in 50 selected images in two sizes (
) in 50 selected images in two sizes ( and
and  ) and obtained
) and obtained  watermarked images. Then we used StirMark and did different attacks to the watermarked images including Blurring, Sharpening, Scaling, adding Gaussian noise, Tampering, data block removal and Cropping. In addition, JPEG compression with different quality factors was applied to the watermarked images. Then, we conducted the watermark detection procedure on every attacked watermarked image. Table 4 shows the PSNR of watermarked images and extracted watermarks. As it is shown in this table, the proposed method outperforms than two related methods in term of PSNR of watermarked images and extracted watermark after different attacks.
watermarked images. Then we used StirMark and did different attacks to the watermarked images including Blurring, Sharpening, Scaling, adding Gaussian noise, Tampering, data block removal and Cropping. In addition, JPEG compression with different quality factors was applied to the watermarked images. Then, we conducted the watermark detection procedure on every attacked watermarked image. Table 4 shows the PSNR of watermarked images and extracted watermarks. As it is shown in this table, the proposed method outperforms than two related methods in term of PSNR of watermarked images and extracted watermark after different attacks.
Finally, as Table 5 shows, the comparison results have demonstrated that our method is capable of detecting watermarks at lower error rates than two related methods and can more effectively stay robust under image processing attacks. Also, Table 6 shows PSNR value of watermarked image by different methods. The best value in each row of these tables has been bolded.
 ) by several methods.
) by several methods.The quality of extracted watermark by proposed method and two related ones versus different attacks are summarized in Tables 7, 8, 9 and 10 for Lena and Baboon with watermark size  , Peppers and Crowd with watermark size
, Peppers and Crowd with watermark size  , respectively. The 2th column of each of these tables represents the attack type and the symbols "AF", "B", "GN", "MF", "S", "GL", "SH", "C", "CAR", "WF" and "JP" denote average filter, blurring, Gaussian noise, median filter, scaling, Gaussian lowpass filter, sharpening, cropping, change aspect ratio, wiener filter and JPEG compression, respectively. The number following each symbol is the parameter with a specific operation. The 2th column of each of these tables represents PSNR of the watermarked image after different attacks, 3th, 4th and 5th columns of each table represent the
, respectively. The 2th column of each of these tables represents the attack type and the symbols "AF", "B", "GN", "MF", "S", "GL", "SH", "C", "CAR", "WF" and "JP" denote average filter, blurring, Gaussian noise, median filter, scaling, Gaussian lowpass filter, sharpening, cropping, change aspect ratio, wiener filter and JPEG compression, respectively. The number following each symbol is the parameter with a specific operation. The 2th column of each of these tables represents PSNR of the watermarked image after different attacks, 3th, 4th and 5th columns of each table represent the  value of extracted watermark. The best value in each row has been bolded.
value of extracted watermark. The best value in each row has been bolded.
 ) with watermark size
) with watermark size  (Figure 11(b)) versus several attacks in different methods.
(Figure 11(b)) versus several attacks in different methods. ) with watermark size
) with watermark size  (Figure 11(b)) versus several attacks in different methods.
(Figure 11(b)) versus several attacks in different methods. ) with watermark size
) with watermark size  (Figure 11(b)) versus several attacks in different methods.
(Figure 11(b)) versus several attacks in different methods. ) with watermark size
) with watermark size  (Figure 11(b)) versus several attacks in different methods.
(Figure 11(b)) versus several attacks in different methods.5. Conclusion
In this paper, a grayscale watermark insertion and extraction schemes were proposed. The proposed method works by modifying the DC value of the original image in frequency domain to create the watermarked image. The embedding procedure is based on fuzzy inference system to locate the best place of watermark insertion. The algorithm was tested with several standard test images and the experimental results demonstrated that it created high-quality images and it was robust versus different attacks. In the future, we are going to change the proposed method such that it can support all attacks by developing a blind method that uses similar idea.
References
Hu M-C, Lou D-C, Chang M-C: Dual-wrapped digital watermarking scheme for image copyright protection. Computers and Security 2007, 26(4):319-330. 10.1016/j.cose.2006.11.007
Shieh J-M, Lou D-C, Chang M-C: A semi-blind digital watermarking scheme based on singular value decomposition. Computer Standards and Interfaces 2006, 28(4):428-440. 10.1016/j.csi.2005.03.006
Gonzales CA, Allman L, McCarthy T, Wendt P, Akansu AN: DCT coding for motion video storage using adaptive arithmetic coding. Signal Processing 1990, 2(2):145-154.
Veeraswamy K, Srinivas Kumar S: Adaptive AC-coefficient prediction for image compression and blind watermarking,. Journal of Multimedia 2008, 3(1):16-22.
Martin V, Chabert M, Lacaze B: An interpolation-based watermarking scheme. Signal Processing 2008, 88(3):539-557. 10.1016/j.sigpro.2007.08.016
Bender W, Gruhl D, Morimoto N, Lu A: Techniques for data hiding. IBM Systems Journal 1996, 35(3-4):313-335.
Schyndel RV, Trikel AZ, Osborn CF: A digital watermark. Proceedings of the 1st IEEE International Conference on Image Processing, 1994 86-90.
Saxena V, Gupta JP: A novel watermarking scheme for JPEG images. WSEAS Transactions on Signal Processing 2009, 5(2):74-84.
Kang X, Zeng W, Huang J: A multi-band wavelet watermarking scheme. International Journal of Network Security 2008, 6(2):121-126.
Wang X-Y, Hou L-M, Wu J: A feature-based robust digital image watermarking against geometric attacks. Image and Vision Computing 2008, 26(7):980-989. 10.1016/j.imavis.2007.10.014
Lee Z-J, Lin S-W, Su S-F, Lin C-Y: A hybrid watermarking technique applied to digital images. Applied Soft Computing 2008, 8(1):798-808. 10.1016/j.asoc.2007.03.011
Parthasarathy AK, Kak S: An improved method of content based image watermarking. IEEE Transactions on Broadcasting 2007, 53(2):468-479.
Langelaar GC, Lagendijk RL: Optimal differential energy watermarking of DCT encoded images and video. IEEE Transactions on Image Processing 2001, 10(1):148-158. 10.1109/83.892451
Cox IJ, Kilian J, Leighton FT, Shamoon T: Secure spread spectrum watermarking for multimedia. IEEE Transactions on Image Processing 1997, 6(12):1673-1687. 10.1109/83.650120
Lu CS, Liao HYM, Sze CJ: Cocktail watermarking on images. Proceedings of the 3rd International Workshop on Information Hiding, 1999 333-347.
Barni M, Bartolini F, Cappellini V, Piva A: A DCT-domain system for robust image watermarking. Signal Processing 1999, 66(3):357-372.
Hsu C-T, Wu J-L: Hidden digital watermarks in images. IEEE Transactions on Image Processing 1999, 8(1):58-68. 10.1109/83.736686
Huang J, Yun QS, Cheng W: Image watermarking in DCT: an embedding strategy and algorithm. Acta Electronica Sinica 2000, 28(4):57-60.
Xie L, Arce GR: Joint wavelet compression and authentication watermarking. Proceedings of the 1998 International Conference on Image Processing, October 1998 427-431.
Zhao Y, Campisi P, Kundur D: Dual domain watermarking for authentication and compression of cultural heritage images. IEEE Transactions on Image Processing 2004, 13(3):430-448. 10.1109/TIP.2003.821552
Hsu C-T, Wu J-L: Hidden digital watermarks in images. IEEE Transactions on Image Processing 1999, 8(1):58-68. 10.1109/83.736686
Hsu C-T, Wu J-L: Multiresolution watermarking for digital images. IEEE Transactions on Circuits and Systems II 1998, 45(8):1097-1101. 10.1109/82.718818
Al-Haj A: Combined DWT-DCT digital image watermarking. Journal of Computer Science 2007, 3(9):740-746.
Mohanty SP, Bhargava BK: Invisible watermarking based on creation and robust insertion-extraction of image adaptive watermarks. ACM Transactions on Multimedia Computing, Communications and Applications 2008., 5(2, article 12):
Reininger RC, Gibson JD: Distributions of the two-dimensional DCT coefficients for images. IEEE Transactions on Communications 1983, 31(6):835-839. 10.1109/TCOM.1983.1095893
Mohanty SP, Ramakrishnan KR, Kankanhalli MS: A dual watermarking technique for images. Proceedings of the 7th ACM International Multimedia Conference, 1999 49-51.
Asatryan D, Asatryan N: Combined spatial and frequency domain watermarking. Proceedings of the 7th International Conference on Computer Science and Information Technologies, 2009 323-326.
Sakr N, Zhao J, Groza VZ: Adaptive digital image watermaking based on predictive embedding and a Dynamic Fuzzy Inference System model. International Journal of Advanced Media and Communication 2007, 1(3):237-264. 10.1504/IJAMC.2007.013917
Borş AG, Pitas I: Image watermarking using block site selection and DCT domain constraints. Optics Express 1998, 3(12):512-523. 10.1364/OE.3.000512
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rahmani, H., Mortezaei, R. & Ebrahimi Moghaddam, M. A New Robust Watermarking Scheme to Increase Image Security. EURASIP J. Adv. Signal Process. 2010, 428183 (2010). https://doi.org/10.1155/2010/428183
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/428183
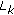 ). The brighter the background, the lower the visibility of the embedded watermark. It is estimated by following relation:
). The brighter the background, the lower the visibility of the embedded watermark. It is estimated by following relation: 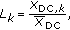
 is the DC coefficient of
is the DC coefficient of  th block and
th block and  is the mean value of DC coefficients of an original image.
is the mean value of DC coefficients of an original image.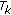 ). The stronger the texture, the lower visibility of embedded watermark. It can be estimated by quantizing the DCT coefficients of a block
). The stronger the texture, the lower visibility of embedded watermark. It can be estimated by quantizing the DCT coefficients of a block 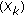 using the JPEG quantization table
using the JPEG quantization table 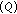 . The latter results are then rounded to the nearest integers. The number of nonzero coefficients is then computed. This number presents the texture of that block:
. The latter results are then rounded to the nearest integers. The number of nonzero coefficients is then computed. This number presents the texture of that block: 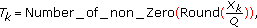
 are coefficients and
are coefficients and  counts nonzero coefficients in
counts nonzero coefficients in 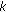 th block.
th block.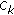 ). The center quarter of an image is perceptually more important than other areas of the image. We estimate location of each block by computing the following ratio:
). The center quarter of an image is perceptually more important than other areas of the image. We estimate location of each block by computing the following ratio: 




























