- Research Article
- Open access
- Published:
A New Inverse Halftoning Method Using Reversible Data Hiding for Halftone Images
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 430235 (2010)
Abstract
A new inverse halftoning algorithm based on reversible data hiding techniques for halftone images is proposed in this paper. The proposed scheme has the advantages of two commonly used methods, the lookup table (LUT) and Gaussian filtering methods. We embed a part of important LUT templates into a halftone image and restore the lossless image after these templates have been extracted. Then a hybrid method is performed to reconstruct a grayscale image from the halftone image. In the image reconstruction process, the halftone image is scanned pixel by pixel. If the scanned pattern surrounding a pixel appeared in the LUT templates, a gray value is directly predicted using the LUT value; otherwise, it is predicted using Gaussian filtering. Experimental results show that the reconstructed grayscale images using the proposed scheme own better quality than both the LUT and Gaussian filtering methods.
1. Introduction
Inverse halftoning is a process which transforms halftone images into grayscale images. Halftone images are binary images that provide a rendition of grayscale images and consists of "0" and "1". It has been widely used in the publishing applications, such as newspapers, e-documents, and magazines. In halftoning process, it needs to use a kernel to carry out the conversion, and the common kernel is like Floyd-Steinberg kernel and is difficult to recover a continuous-tone image through halftone manipulation, conversion, compression, and so forth. In the past few years, many efficient inverse halftoning algorithms have been proposed, but there is no way to construct a perfect gray image from the given halftone image. There exist several inverse halftoning methods, including kernel estimation [1], wavelet [2], filtering [3, 4], and set theoretic approaches [5]. Most of these methods can obtain good reconstruction image quality but require relatively high computational complexity.
The halftoning and inverse halftoning processes can be regarded as the encoding and decoding processes of vector quantization. Therefore, the codebook design methods can be applied to build the inverse halftoning lookup tables [6, 7]. The content of a table entry is the centroid of the input samples that are mapped to this entry. The results are optimal in the sense of minimizing the MSE for a given halftone method. Although the table lookup method has the advantages of good reconstructed quality and fast speed, it faces the empty cell problem in which no or very few training samples are mapped to a specific halftone pattern.
In this paper, a reversible data hiding scheme for halftone images is proposed to embed specified information to improve the LUT-based inverse halftoning method. We embed a part of important LUT templates into a halftone image and generate a stego image in the data embedding process. Then, we can restore the halftone image without any distortion from the stego image after these templates have been extracted. Finally, we can obtain higher quality reconstructed images than the traditional LUT method by performing the proposed hybrid method with the extracted templates and the halftone image. The rest of the paper is organized as follows. Section 2 introduces related works about inverse halftoning methods and reversible data hiding methods for binary images. Section 3 presents the proposed reversible data hiding method for halftone images and the proposed hybrid method for inverse halftoning. Section 4 shows the experimental results and discussions, and the final section summarizes this paper.
2. Related Works
In this section, we introduce the methods which are related to inverse halftoning techniques including LUT-based and the Gaussian filtering methods. In addition, recently used reversible data hiding techniques for binary images are also introduced.
2.1. LUT-Based Method
The LUT-based method includes two procedures: the LUT buildup and the LUT-based inverse halftoning (LIH) procedures. The LUT buildup procedure is to build the LUT information by scanning selected grayscale images and their corresponding halftone images with a  and
and  template. Figure 1 shows the
template. Figure 1 shows the  and
and  templates with symbol X denoting the estimated pixel, respectively. Template is used as a sliding window to build up the LUT. In the LIH procedure, a grayscale image can be reconstructed from the given halftone image using the LUT information. The LUT information contains a set of pairs of binary pattern and its corresponding estimated gray value. Assume that there are
templates with symbol X denoting the estimated pixel, respectively. Template is used as a sliding window to build up the LUT. In the LIH procedure, a grayscale image can be reconstructed from the given halftone image using the LUT information. The LUT information contains a set of pairs of binary pattern and its corresponding estimated gray value. Assume that there are  training image pair sets and
training image pair sets and  represents the
represents the  th pair, where
th pair, where  denotes the
denotes the  th original image and
th original image and  the corresponding halftone image of
the corresponding halftone image of  . The LUT buildup and LIH procedures using
. The LUT buildup and LIH procedures using  template
template  are described as follows.
are described as follows.
Procedure LUT Buildup
Step 1.
Let arrays LUT and
and  be zero as the initial values. LUT
be zero as the initial values. LUT is used to record the mapped gray value corresponding to a specific binary template with index
is used to record the mapped gray value corresponding to a specific binary template with index  which appears in the input halftone image, and
which appears in the input halftone image, and  is used to store the occurrence frequency of this specific binary template in the halftone image. Select
is used to store the occurrence frequency of this specific binary template in the halftone image. Select  training grayscale images, and generate their corresponding halftone images, respectively.
training grayscale images, and generate their corresponding halftone images, respectively.
Step 2.
Select one image from the  training grayscale images. Scan the selected image and its corresponding halftone image in raster order with the template
training grayscale images. Scan the selected image and its corresponding halftone image in raster order with the template  . The index
. The index  for a pixel X can be calculated using (1), where
for a pixel X can be calculated using (1), where  represents different locations on the template
represents different locations on the template  . Since there are totally 16 locations on the template
. Since there are totally 16 locations on the template  , the value of
, the value of  ranges from 0 to 65535. Then, the sum of the template occurrence frequencies and the sum of the gray values on the image pixel X can be computed as (2):
ranges from 0 to 65535. Then, the sum of the template occurrence frequencies and the sum of the gray values on the image pixel X can be computed as (2):


Step 3.
Repeat Step 2, until all  images are selected.
images are selected.
Step 4.
The predicted gray value for a specified  pattern with indexed I can be computed as
pattern with indexed I can be computed as

Figure 2(a) shows an example to build LUT by performing Step 2 of LUT buildup algorithm.
Procedure LIH
Step 1.
Perform the above-mentioned LUT buildup algorithm to build LUT.
Step 2.
Scan a halftone image in raster order with template  , and compute the template index
, and compute the template index  using (1). The estimated gray value on pixel X can be obtained and denoted as
using (1). The estimated gray value on pixel X can be obtained and denoted as  .
.
Step 3.
Output the estimated grayscale image.
Figure 2(b) shows an example to build LUT by performing of LIH algorithm.
Note that, some binary patterns in the input halftone image may not exist in the training images. In this situation, we will apply filters to estimate the mean gray pixel.
Though the LUT-based inverse halftoning method is easily implemented, there exists a disadvantage of this method, the constructed LUT information must be sent to the receiver.
2.2. Gaussian Filtering Method
Gaussian filtering is a smoothing algorithm for images. Equation (4) denotes a 2D Gaussian function, and  is the standard deviation of a Gaussian distribution. In the implementation of inverse halftoning using Gaussian filtering, the binary pixel value 0 and 1 in the input halftone image will be regarded as 0 and 255, respectively. A weight mask with specified size and contents should be determined according to the use of Gaussian distribution with parameter
is the standard deviation of a Gaussian distribution. In the implementation of inverse halftoning using Gaussian filtering, the binary pixel value 0 and 1 in the input halftone image will be regarded as 0 and 255, respectively. A weight mask with specified size and contents should be determined according to the use of Gaussian distribution with parameter  . In the inverse halftoning process, the halftone image is scanned pixel by pixel in a raster order by moving the sliding mask. The output gray value on the corresponding central pixel of the mask is estimated via the summation of the weight value on the mask content multiplying by the binary values on the neighboring pixels. If the value of
. In the inverse halftoning process, the halftone image is scanned pixel by pixel in a raster order by moving the sliding mask. The output gray value on the corresponding central pixel of the mask is estimated via the summation of the weight value on the mask content multiplying by the binary values on the neighboring pixels. If the value of  is larger, the resulting image will be more smoothing. In the inverse halftoning process using Gaussian filtering, the following equation of 2D Gaussian distribution is generally used to determine the mask:
is larger, the resulting image will be more smoothing. In the inverse halftoning process using Gaussian filtering, the following equation of 2D Gaussian distribution is generally used to determine the mask:

2.3. Reversible Data Hiding for Binary Images
Reversible data hiding can embed secret message in a reversible way. Relatively large amounts of secret data are embedded into a cover image so that the decoder can extract the hidden secret data and restore the original cover image without any distortion. Recently, a boundary-based PWLC method has been presented [8]. This method defines the same continuous 6 edge pixels as an embeddable block through searching for binary image edges. And then one can embed data in the pair of the third and fourth edge pixels. A reversible data hiding method for error-diffused halftone images is proposed [9]. This method employs statistics feature of pixel block patterns to embed data and utilizes the HVS characteristics to reduce the introduced visual distortion. The method is suitable for the applications, where the content accuracy of the original halftone image must be guaranteed, and it is easily extended to the field of halftone image authentication. However, these two methods have a drawback that the capacity of data hiding is still limited.
3. Proposed Method
The proposed inverse halftoning method based on reversible data hiding techniques can be divided into two phases: the embedding process and the extracting process. Figure 3(a) shows the diagram of the proposed method. In the embedding process, a grayscale image is transferred into a halftone image by error diffusion process. Then pattern selection is performed to determine the pattern pairs for the use in reversible data hiding. Meanwhile, a part of LUT templates are selected to keep high quality of recovery images in the reconstruction process. These templates along with the pattern pairs will be encoded in bit streams and embedded into the halftone image. The data embedding operation is performed based on pattern substitution. In the data extracting process, the pattern pairs and LUT templates are first extracted. The halftone image can be losslessly restored after the data extraction. Finally, we can reconstruct a good quality grayscale image from the halftone one with the aid of LUT templates. The proposed scheme has the advantages of two commonly used methods, the lookup table (LUT) and Gaussian filtering methods. We embed a part of important LUT templates into a halftone image and restore the lossless image after these templates had been extracted.
3.1. Data Hiding with Pattern Substitution for Halftone Images
The proposed method of reversible halftone data hiding technique uses pattern substitution method to embed and extract data into halftone images. The original image is partitioned into a set of nonoverlapping  blocks. There are totally 29 different patterns. Therefore, each pattern is uniquely associated with an integer in the range of 0 to 511. In most cases, many patterns never appear in an image.
blocks. There are totally 29 different patterns. Therefore, each pattern is uniquely associated with an integer in the range of 0 to 511. In most cases, many patterns never appear in an image.
In this study, all patterns are classified into two groups, used and unused. For each used pattern  , an unused pattern
, an unused pattern  , its content is the most closest to pattern
, its content is the most closest to pattern  , will be selected to form a pair for data embedding. In the data embedding process, the original halftone image is partitioned into a group of
, will be selected to form a pair for data embedding. In the data embedding process, the original halftone image is partitioned into a group of  nonoverlapping patterns. Then, any pattern
nonoverlapping patterns. Then, any pattern  on the halftone image with the same content of
on the halftone image with the same content of  will be selected to embed 1-bit data. If a data bit "0" is embedded on
will be selected to embed 1-bit data. If a data bit "0" is embedded on  , then the content of
, then the content of  remains as
remains as  . If a data bit "1" is embedded on
. If a data bit "1" is embedded on  , then the content of
, then the content of  is updated as the content of pattern
is updated as the content of pattern  . This scheme works because patterns
. This scheme works because patterns  ,
,  look similar. In data extraction process, the embedded message is obtained depending on the patterns
look similar. In data extraction process, the embedded message is obtained depending on the patterns  ,
,  when the test image is scanned. For example, assume that the highest frequent pattern in the image is
when the test image is scanned. For example, assume that the highest frequent pattern in the image is  and its corresponding unused pattern is
and its corresponding unused pattern is  . We can embed three secret data bits (e.g., 011) into the following
. We can embed three secret data bits (e.g., 011) into the following  image block with the proposed pattern substitution method. The image is firstly divided into four nonoverlapped
image block with the proposed pattern substitution method. The image is firstly divided into four nonoverlapped  patterns, and these patterns are scanned horizontally from top to buttom. If the content of the pattern PH is encountered, then check the bit value which is currently embedded. If the bit value is "0," then keep the content as PH. If the value is "1," then we replace PH with the PL pattern. This example of data embedding is shown in Figure 3(b).
patterns, and these patterns are scanned horizontally from top to buttom. If the content of the pattern PH is encountered, then check the bit value which is currently embedded. If the bit value is "0," then keep the content as PH. If the value is "1," then we replace PH with the PL pattern. This example of data embedding is shown in Figure 3(b).
To achieve a higher capacity of embedding data, more pattern pairs should be determined, whose steps can be presented as follows.
-
(1)
Partition the original image into nonoverlapping
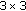 blocks.
blocks. -
(2)
Compute the occurrence frequencies for all appeared patterns. Sort these used patterns decreasingly, and denote them as
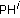 according to their occurrence frequencies. For instance,
according to their occurrence frequencies. For instance, 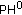 is the pattern with the highest occurrence frequency.
is the pattern with the highest occurrence frequency. -
(3)
Find out all unused patterns. Assume that there are totally TC unused patterns; TC pairs of patterns (
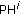 ,
, 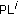 ) are selected to perform the data embedding operation, where the distance of pattern pair (
) are selected to perform the data embedding operation, where the distance of pattern pair (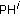 ,
,  ) owns the minimal distance. Based on the raster scan order, pattern PH and PL can be denoted as 9 elements PH0, PH1, PH2,…, PH8 and PL0, PL1, PL2,…, PL8, respectively. The calculation of pattern similarity for pattern PH and PL can be defined using the following distance equation:
) owns the minimal distance. Based on the raster scan order, pattern PH and PL can be denoted as 9 elements PH0, PH1, PH2,…, PH8 and PL0, PL1, PL2,…, PL8, respectively. The calculation of pattern similarity for pattern PH and PL can be defined using the following distance equation: 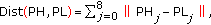 (5)
(5)where
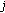 is the location in the
is the location in the  block.
block. -
(4)
Search all blocks in the original image. As long as we come across a pattern in the
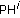 , if a bit "0" is embedded, the block remains as
, if a bit "0" is embedded, the block remains as  ; otherwise, the block is updated as the pattern
; otherwise, the block is updated as the pattern  .
.
The maximum embedding capacity of the proposed data embedding method can be denoted as  , where
, where  represents the occurrence frequency of pattern
represents the occurrence frequency of pattern  in the image and
in the image and  is the number of selected pairs.
is the number of selected pairs.
However, the image quality of stego image generated using the proposed method is not very well in the visual effect. To consider human visual effect, we should take notice about some situations which will cause "congregation" effect around the center, corners, or lines on the  block. These cases are displayed in Figure 4. To avoid these cases when a pattern replacement occurs, we apply the following equation to replace (5):
block. These cases are displayed in Figure 4. To avoid these cases when a pattern replacement occurs, we apply the following equation to replace (5):

where

The matching pairs of  and
and  should be stored for the recovery and denoted as the Secret Header (SH) with size of
should be stored for the recovery and denoted as the Secret Header (SH) with size of  bits. Therefore, we should embed the secret header SH to the cover halftone images. Figure 5 is the secret header SH, and the data hiding process for SH will be discussed in Section 3.3.
bits. Therefore, we should embed the secret header SH to the cover halftone images. Figure 5 is the secret header SH, and the data hiding process for SH will be discussed in Section 3.3.
3.2. The Determination of Important LUT Templates
The proposed method is a kind of hybrid inverse halftoning method which has the advantages of Gaussian filtering and LUT methods. For a small image block which is the same size as the used template size in a halftone image, if the difference between the predicted value and the original real gray value using Gaussian filtering method is larger than the difference using LUT method with a specified template, it means that LUT method can obtain a better result than Gaussian filtering on the image block. Figure 6 shows an example for the comparison of image quality loss using these two methods.
But it does not guarantee that the LUT method with this template always works better in other image blocks than using Gaussian filter. So we should sum up the difference values for a specified template to all image blocks on the halftone image. If the sum of differences with LUT method is smaller than the sum with Gaussian filter, then this template is worth being recorded and embedded. This means that the LUT template can obtain a higher image quality than using Gaussian filtering method in the image recovery process. However, only a part of important templates which save larger quality loss are selected to embed since the embedding capacity is limited for a halftone image. In the grayscale image recovery process, we scan the halftone image by checking the templates. If the current template is one of the embedded templates, then LUT is used to predict the gray value; otherwise, Gaussian filtering method is applied to predict the value. Figure 7 displays the flowchart of the LUT entry selection.
implementation,  and
and  templates are considered for the LUT method. We introduce the operating procedure of using the proposed method with a
templates are considered for the LUT method. We introduce the operating procedure of using the proposed method with a  template as bellows, and the case with a
template as bellows, and the case with a  template is similar.
template is similar.
Procedure LUT Temple Selection with a Template of Size 
Step 1.
Perform the LUT buildup procedure, and proceed to train the input original grayscale and halftone images. Apply the LIH procedure to an input halftone image  , and generate a corresponding predicted image
, and generate a corresponding predicted image  .
.
Step 2.
Perform the inverse halftoning using Gaussian filtering for image  , and generate a predicted image
, and generate a predicted image  .
.
Step 3.
Compute the difference of the absolute values of  minus
minus  and G minus
and G minus  using the following equation:
using the following equation:

If the  value is greater than zero, it means that the LUT method can obtain a better predicted value than Gaussian method on the pixel with location
value is greater than zero, it means that the LUT method can obtain a better predicted value than Gaussian method on the pixel with location  .
.
Step 4.
Scan the image block by block with block size  . For a processed block, if
. For a processed block, if  is the predicted position and the image block on the halftone image is with index
is the predicted position and the image block on the halftone image is with index  , then the sum of difference
, then the sum of difference  can be accumulated as
can be accumulated as

 can be regarded as the quality improvement of the predicted image by replacing Gaussian filtering with the LUT method.
can be regarded as the quality improvement of the predicted image by replacing Gaussian filtering with the LUT method.
Step 5.
Sort  decreasingly, and generate the corresponding templates index
decreasingly, and generate the corresponding templates index  , where
, where  . Since the embedding capacity is limited, we can only embed part of the top LUT templates into the halftone image. The total quality improvement is denoted as
. Since the embedding capacity is limited, we can only embed part of the top LUT templates into the halftone image. The total quality improvement is denoted as  , where
, where  represents the number of embedded templates.
represents the number of embedded templates.
Figure 8 shows an example of the sum of differences  for Lena image, where
for Lena image, where  -axis represents the pattern index
-axis represents the pattern index  in the halftone image with
in the halftone image with  templates and
templates and  -axis represents the
-axis represents the  value. If
value. If  is greater than zero, it means that the LUT-based method works better than Gaussian filtering method on the pixel value prediction under all image blocks with the same context of the template indexed by
is greater than zero, it means that the LUT-based method works better than Gaussian filtering method on the pixel value prediction under all image blocks with the same context of the template indexed by  .
.
Assume that  is the number of parts of top LUT templates to be embedded into the halftone image using
is the number of parts of top LUT templates to be embedded into the halftone image using  templates, and
templates, and  is the number of parts of top LUT templates to be embedded using
is the number of parts of top LUT templates to be embedded using  templates, respectively.
templates, respectively.  and
and  can be computed according to (10) and (11):
can be computed according to (10) and (11):


In (9), as mentioned above, parameter TC represents the number of pairs used in data embedding process. The maximum value of TC is 256 when  templates are applied, and it requires 8 bits to the storage. We also need
templates are applied, and it requires 8 bits to the storage. We also need  bits to store the content of all matching pairs of templates and one bit to store the template type to discriminate the usage of
bits to store the content of all matching pairs of templates and one bit to store the template type to discriminate the usage of  and
and  templates. If
templates. If  represents the number of LUT templates which are embedded into the cover image, 10 bits are used to store
represents the number of LUT templates which are embedded into the cover image, 10 bits are used to store  value in our experiments.
value in our experiments.
Finally, we can compare the two values of  and
and  ; if
; if  is larger, it means that the quality improvement using
is larger, it means that the quality improvement using  templates is better than the case of using
templates is better than the case of using  templates; otherwise,
templates; otherwise,  templates are used in the data embedding process.
templates are used in the data embedding process.
Assume that the template type is DT and the number of embedded LUT templates is  . The LUT information for each template should contain two parts, the template index
. The LUT information for each template should contain two parts, the template index  and the predicted gray value
and the predicted gray value  ,
,  . Figure 9 displays the LUT information and structure and is denoted as LH (LUT data header).
. Figure 9 displays the LUT information and structure and is denoted as LH (LUT data header).
3.3. Overhead Information and Data Embedding
The overhead information includes two kinds of data; SH is the pattern pairs information (Figure 5) for data embedding, and LH is the important LUT template information (Figure 9) for improving the quality of recovery images. Since different images have different contents of SH and LH. We should embed the overhead information into the halftone image for image recovery. In the data embedding process, SH and LH are converted into a binary bit stream. Then SH is embedded into image and LH is embedded after the embedded SH. The embedding method is implemented by pattern matching approach according to the order of the image scanning, from top to bottom horizontally. If one pattern  is encountered and the embedded bit value is currently 0, then the pattern
is encountered and the embedded bit value is currently 0, then the pattern  is kept; otherwise,
is kept; otherwise,  is replaced by
is replaced by  . The output stego image in this stage is denoted as
. The output stego image in this stage is denoted as  .
.
Although the SH is embedded in the data embedding process, the receiver cannot extract data correctly from the stego image  since the receiver does not know the SH pair information before starting the pair-based extracting process. To overcome this problem, we define a region with the same size of SH length
since the receiver does not know the SH pair information before starting the pair-based extracting process. To overcome this problem, we define a region with the same size of SH length  bits, and it is located in the last row of cover image. The pixel values on this region in the stego image are denoted as
bits, and it is located in the last row of cover image. The pixel values on this region in the stego image are denoted as  . Then we embed
. Then we embed  into stego image
into stego image  using the proposed pattern substitution scheme again. In this stage,
using the proposed pattern substitution scheme again. In this stage,  is regarded as the cover image, and the pattern pair information PH is applied in the data embedding process. Finally, the bit stream of SH is then directly "paste" into the last row of
is regarded as the cover image, and the pattern pair information PH is applied in the data embedding process. Finally, the bit stream of SH is then directly "paste" into the last row of  pixel by pixel, and a new stego image is generated and denoted as
pixel by pixel, and a new stego image is generated and denoted as  . Figure 10 shows the flowchart of data embedding; Figure 10(a) embeds SH and LH into the halftone image in horizontal scanning and generates a stego image
. Figure 10 shows the flowchart of data embedding; Figure 10(a) embeds SH and LH into the halftone image in horizontal scanning and generates a stego image  ; Figure 10(b) extracts
; Figure 10(b) extracts  pixels from the last row of stego image
pixels from the last row of stego image  and is denoted as
and is denoted as  ; in Figure 10(c),
; in Figure 10(c),  is then embedded into the stego image
is then embedded into the stego image  with pair-based method and generated another stego image
with pair-based method and generated another stego image  .
.
3.4. Data Extract and Recovering Grayscale Image
In data extracting process, we extract  bits of SH from the last raw of a stego image
bits of SH from the last raw of a stego image  and get the pattern information of
and get the pattern information of  and
and  from SH data. Then we start scanning the stego image from top to bottom. If
from SH data. Then we start scanning the stego image from top to bottom. If  is met, bit 0 is extracted; otherwise, bit 1 is extracted. The extracted length of bit stream is the same with SH's and denoted as
is met, bit 0 is extracted; otherwise, bit 1 is extracted. The extracted length of bit stream is the same with SH's and denoted as  , and
, and  is copied to the last raw of image to replace the content of SH. Then we can continue to scan image to extract the embedded secret header of LUT information as
is copied to the last raw of image to replace the content of SH. Then we can continue to scan image to extract the embedded secret header of LUT information as  . All patterns of
. All patterns of  are replaced by
are replaced by  in the extracting process to recover the original halftone image. Figure 11 displays the data extracting process and the original halftone image reconstruction.
in the extracting process to recover the original halftone image. Figure 11 displays the data extracting process and the original halftone image reconstruction.
Finally, we can reconstruct the grayscale images for the original halftone image using the proposed hybrid method. In the image recovery process, we first predict the grayscale image from the restored halftone image by Gaussian filtering method. Then we rescan the restored halftone image again to find the pattern with the same contents of the embedded LUT template  . If this case is met, we will update the corresponding central pixel value in the predicted grayscale image with the value
. If this case is met, we will update the corresponding central pixel value in the predicted grayscale image with the value  . Finally, a better quality of predicted grayscale image can be obtained.
. Finally, a better quality of predicted grayscale image can be obtained.
4. Experimental Results
Four  error-diffused halftone images, "Lena," "Pepper," "Airplane," and "Baboon," are selected to test the performance of the proposed method. These halftone images are obtained by performing Floyd-Steinberg error diffusion filtering on the 8-bit gray-level images. Figure 12 shows the pattern histogram of the halftone image Lena with
error-diffused halftone images, "Lena," "Pepper," "Airplane," and "Baboon," are selected to test the performance of the proposed method. These halftone images are obtained by performing Floyd-Steinberg error diffusion filtering on the 8-bit gray-level images. Figure 12 shows the pattern histogram of the halftone image Lena with  -axis indicating the pattern index ranging from 0 to 511 and
-axis indicating the pattern index ranging from 0 to 511 and  -axis indicating the occurrence frequency of each pattern index. The highest peak among the histograms is with value 1058, and the number of zero value is totally 134. Figure 13 displays the top ten matching patterns which own the highest occurrence frequency in the halftone image Lena. In addition, we have also applied the proposed method on other images including Pepper, Baboon, and Airplane. Figure 14 shows the original grayscale images. Figures 15(a), 15(d), 15(g), and 15(j) are the generated halftone images from the images in Figure 14, respectively. Figures 15(b), 15(e), 15(h), and 15(k) are the generated stego images with 2072, 2329, 3086, and 2603 bits of data embedded, respectively. Figures 15(c), 15(f), 15(i), and 15(l) show the generated stego images with maximum capacity, respectively.
-axis indicating the occurrence frequency of each pattern index. The highest peak among the histograms is with value 1058, and the number of zero value is totally 134. Figure 13 displays the top ten matching patterns which own the highest occurrence frequency in the halftone image Lena. In addition, we have also applied the proposed method on other images including Pepper, Baboon, and Airplane. Figure 14 shows the original grayscale images. Figures 15(a), 15(d), 15(g), and 15(j) are the generated halftone images from the images in Figure 14, respectively. Figures 15(b), 15(e), 15(h), and 15(k) are the generated stego images with 2072, 2329, 3086, and 2603 bits of data embedded, respectively. Figures 15(c), 15(f), 15(i), and 15(l) show the generated stego images with maximum capacity, respectively.
The stego images of data hiding using the proposed method: (a), (d), (g), and (j) the halftone image generated by error diffusion; (b) and (h) the stego images of embedding two pairs of templates; (e) and (k) the stego images of embedding three pairs of templates; (c), (f), (i), and (l) the stego image of hiding all pairs of templates.
Figure 16 shows the difference between the generated stego images with and without applying the weight adjusting operation. Obviously, the stego image with weight adjusting operation owns better perceptive quality than the other one since the operation can reduce the possibility of forming black spots.
Table 1 shows the used templates, the number of selected pairs and embedding capacities using the proposed method for different images. The embedding capacities for image Lena, Pepper, and Airplane are all about 25000 bits. But the capacity for image Baboon is only 9544 bits. This is because the number of zero patterns is smaller than the other three images. It means that there is more different "texture" patterns existing in the Baboon halftone image. Due to the smaller embedding capacity, only few templates information are selected to embed into the halftone image. In the case for Baboon image,  template is used to be replaced by
template is used to be replaced by  template to obtain a better quality of reconstructed image.
template to obtain a better quality of reconstructed image.
To evaluate the performance of the proposed method, different inverse halftoning methods are used for comparison. They include the Gaussian filtering with parameter  , traditional LUT and Edge-based LUT methods with ten images for training. Table 2 shows the PSNR values for the recovery images using these different methods. Experimental results show that the reconstructed grayscale images using the proposed scheme own better quality than Gaussian filtering, traditional LUT, and Edge-based LUT methods. Figure 17 shows the experimental results for image Lena using different methods. The reconstructed image using Gaussian filtering seems to be "blurring," and the reconstructed one using LUT and ELUT will show some noises on the image. In the experiments of LUT and ELUT, we used ten common images for training to obtain the corresponding LUT information. In the reconstruction process, if the pattern was not in the training LUT, we restored the predicted pixel by Gaussian filtering.
, traditional LUT and Edge-based LUT methods with ten images for training. Table 2 shows the PSNR values for the recovery images using these different methods. Experimental results show that the reconstructed grayscale images using the proposed scheme own better quality than Gaussian filtering, traditional LUT, and Edge-based LUT methods. Figure 17 shows the experimental results for image Lena using different methods. The reconstructed image using Gaussian filtering seems to be "blurring," and the reconstructed one using LUT and ELUT will show some noises on the image. In the experiments of LUT and ELUT, we used ten common images for training to obtain the corresponding LUT information. In the reconstruction process, if the pattern was not in the training LUT, we restored the predicted pixel by Gaussian filtering.
Figure 18 shows the results of image Airplane using different methods, and we extract a part of the reconstructed image to enlarge for comparison. We see that Gaussian filtering results in a visual pleasing but quite blurred image, while LUT and ELUT result in a noisy image. Table 2 displays the PSNR values of reconstructed images using different methods. The proposed method can increase 1.3 dB on PSNR than Gaussian filtering, 1.5 dB than LUT method, and 0.53 dB than ELUT method. It represents the high feasibility of the proposed method.
The used algorithms of LUT, ELUT, and Gaussian filtering in our experiments can be implemented in the raster fashion, the number of operations per pixel is all less than 500, and the time complexity of these methods can be denoted as  for the image of size
for the image of size  . The proposed method can be actually regarded as a hybrid scheme of the LUT and Gaussian filtering methods, but it requires another image scan to extract the embedded important LUT information from the stego halftone image before performing the inverse halftoning. Therefore, the computational complexity of the proposed method is slightly higher than that of the three methods. But the total operation number per pixel using the proposed method is still less than 500. We compare the complexity for several different inverse halftoning methods, and the results are shown in Table 3. The computational complexity is estimated from algorithms given in the corresponding references. Low means a number fewer than 500 operations per pixel, median denotes 500–2000 operations per pixel, and high means more than 2000 operations required.
. The proposed method can be actually regarded as a hybrid scheme of the LUT and Gaussian filtering methods, but it requires another image scan to extract the embedded important LUT information from the stego halftone image before performing the inverse halftoning. Therefore, the computational complexity of the proposed method is slightly higher than that of the three methods. But the total operation number per pixel using the proposed method is still less than 500. We compare the complexity for several different inverse halftoning methods, and the results are shown in Table 3. The computational complexity is estimated from algorithms given in the corresponding references. Low means a number fewer than 500 operations per pixel, median denotes 500–2000 operations per pixel, and high means more than 2000 operations required.
5. Conclusions
A new inverse halftoning algorithm based on reversible data hiding techniques for halftone images is proposed in this paper. We embed a part of important LUT templates into a halftone image and restore the lossless image after these templates have been extracted. Then a hybrid method is performed to reconstruct a grayscale image from the halftone image. Experimental results show that the proposed scheme outperformed Gaussian filtering, LUT, and ELUT methods. The proposed method can be also modified by selecting different filtering methods for practical applications.
References
Wong PW: Inverse halftoning and kernel estimation for error diffusion. IEEE Transactions on Image Processing 1995, 4(4):486-498. 10.1109/83.370677
Xiong Z, Orchard MT, Ramchandran K: Inverse halftoning using wavelets. Proceedings of the IEEE International Conference on Image Processing (ICIP '96), September 1996 1: 569-572.
Fan Z: Retrieval of images from digital halftones. Proceedings of the IEEE International Symposium on Circuits Systems, 1992 313-316.
Kite TD, Damera-Venkata N, Evans BL, Bovik AC: A fast, high-quality inverse halftoning algorithm for error diffused halftones. IEEE Transactions on Image Processing 2000, 9(9):1583-1592. 10.1109/83.862639
Chang P-C, Yu C-S, Lee T-H: Hybrid LMS-MMSE inverse halftoning technique. IEEE Transactions on Image Processing 2001, 10(1):95-103. 10.1109/83.892446
Meşe M, Vaidyanathan PP: Look-up table (LUT) method for inverse halftoning. IEEE Transactions on Image Processing 2001, 10(10):1566-1578. 10.1109/83.951541
Chung K-L, Wu S-T: Inverse halftoning algorithm using edge-based lookup table approach. IEEE Transactions on Image Processing 2005, 14(10):1583-1589.
Tsai C-L, Chiang H-F, Fan K-C, Chung C-D: Reversible data hiding and lossless reconstruction of binary images using pair-wise logical computation mechanism. Pattern Recognition 2005, 38(11):1993-2006. 10.1016/j.patcog.2005.03.001
Pan J-S, Luo H, Lu Z-M: Look-up table based reversible data hiding for error diffused halftone images. Informatica 2007, 18(4):615-628.
Hein S, Zakhor A: Halftone to continuous-tone conversion of error-diffusion coded images. IEEE Transactions on Image Processing 1995, 4(2):208-216. 10.1109/83.342186
Stevenson RL: Inverse halftoning via MAP estimation. IEEE Transactions on Image Processing 1997, 6(4):574-583. 10.1109/83.563322
Acknowledgments
This work was supported by the National Science Council, Taiwan, under Grants 99-2220-E-327-001 and 99-2221-E-328-001.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, JH., Wu, MY. & Wu, HJ. A New Inverse Halftoning Method Using Reversible Data Hiding for Halftone Images. EURASIP J. Adv. Signal Process. 2010, 430235 (2010). https://doi.org/10.1155/2010/430235
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/430235



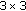 blocks.
blocks.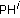 according to their occurrence frequencies. For instance,
according to their occurrence frequencies. For instance, 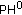 is the pattern with the highest occurrence frequency.
is the pattern with the highest occurrence frequency.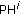 ,
, 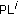 ) are selected to perform the data embedding operation, where the distance of pattern pair (
) are selected to perform the data embedding operation, where the distance of pattern pair (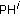 ,
,  ) owns the minimal distance. Based on the raster scan order, pattern PH and PL can be denoted as 9 elements PH0, PH1, PH2,…, PH8 and PL0, PL1, PL2,…, PL8, respectively. The calculation of pattern similarity for pattern PH and PL can be defined using the following distance equation:
) owns the minimal distance. Based on the raster scan order, pattern PH and PL can be denoted as 9 elements PH0, PH1, PH2,…, PH8 and PL0, PL1, PL2,…, PL8, respectively. The calculation of pattern similarity for pattern PH and PL can be defined using the following distance equation: 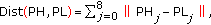
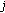 is the location in the
is the location in the  block.
block.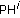 , if a bit "0" is embedded, the block remains as
, if a bit "0" is embedded, the block remains as  ; otherwise, the block is updated as the pattern
; otherwise, the block is updated as the pattern  .
.













