- Research Article
- Open access
- Published:
Multiharmonic Frequency Tracking Method Using The Sigma-Point Kalman Smoother
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 467150 (2010)
Abstract
Several groups have proposed the state-space approach to tracking time-varying frequencies of multiharmonic quasiperiodic signals. The extended Kalman filter/smoother (EKF/EKS) is one of the common frequency tracking approaches seen in the literature. We introduce a multiharmonic frequency tracker based on the forward-backward statistical linearized Sigma-Point Kalman smoother (FBSL-SPKS) and compare its performance to that of the extended Kalman smoother (EKS). In all cases the FBSL-SPKS tracker outperformed the EKS tracker over a wide range of signal-to-noise (SNR) ratios. We also demonstrate its superior performance on real signals.
1. Introduction
Many natural signals contain nearly periodic rhythms with slowly varying morphologies. Example signals with this property include tremor, speech, electrocardiogram (ECG), and arterial blood pressure (ABP). In many applications the instantaneous frequency (IF) of these signals contains useful information for further analysis.
Many signal processing methods have been applied to the problem of multiharmonic frequency tracking in quasiperiodic signals. Especially, the pitch tracking in the speech signal analysis is one of the most common applications of multiharmonic frequency tracking. Pitch detection/tracking algorithms can be roughly categorized into three groups: time-domain methods such as zero-crossing, frequency-domain methods, and time-frequency-domain methods. All pitch tracking methods apply the frame-by-frame analysis due to the nature of human voice [1]. Recently Tabrikian et al. proposed the maximum a posteriori (MAP) probability pitch tracking method using harmonic model [2]. They implemented the MAP estimator by a dynamic programming procedure based on measurement collected over several frames. However, these frame-by-frame based algorithms are always not applicable especially when a local signal stationarity cannot be assumed. There are other methods that have been applied to track rhythmicity (harmonic components) in nonstationary quasiperiodic signals based on adaptive schemes [3]. The advantage of using these adaptive schemes is that one can track rhythmicity (frequencies) recursively as signal samples are acquired.
In this paper we use a Fourier series representation, which is shown in (1) Section 2.1, of multiharmonic quasiperiodic signals in which the amplitudes, phases, and frequencies are allowed to change slowly over time. The application of state space methods to continuously track the amplitudes, phases, and frequencies was pioneered by Parker and Anderson in [4] with many subsequent investigations [5–9]. Recently there have been several proposed methods based on particle filters [10, 11] which are highly computationally intensive and hence practically intractable.
The Kalman filter (KF) recursively estimates the optimal state of a linear state space system driven by Gaussian noise by minimizing the MSE [12]. However, it cannot be applied directly to frequency tracking because our state space model has nonlinearity due to the relationship between frequencies and observed signals. There are many types of generalizations of the KF for the case of a nonlinear state space model. The extended Kalman filter (EKF) uses a local linear approximation of the model. The algorithm is relatively simple and faster than other generalizations of the KF because it relies on a first-order Taylor series approximation of the nonlinear system around the estimate of the current state. The Sigma-Point Kalman filter (SPKF) is another generalization to nonlinear state-space models, which includes the Unscented Kalman filter (UKF) [13], Central Difference Kalman filter (CDKF) [14], and their square-root variants [15]. Like the EKF, the SPKF approximates the state distribution by a Gaussian Random Variable. The SPKF uses a deterministic sampling approach to approximate the probability density of the state-error and noise covariances by a set of carefully chosen sample points known as sigma-points. These sigma-points are chosen in such a way that they completely capture the mean and covariance of the corresponding densities. These sigma-points are then propagated through the true nonlinear system, with the posterior mean and covariance estimated using simple weighted averaging. This approach captures the posterior mean and covariance accurately to the 2nd order (3rd order is achieved for symmetric distributions) compared to EKF which only achieves 1st-order accuracy. Another advantage of the SPKF over other Kalman generalizations is that it maintains the same order of computational complexity as the EKF.
The Kalman smoother (KS) is a noncausal version of the KF. Typically, smoothers can achieve better estimates than filters since they deal with more measurements with proper design. We proposed a tremor frequency tracking method utilizing the extended Kalman smoother (EKS) in [16, 17]. However, we are unaware of any literature that investigates the estimation accuracy of smoothers in the multiharmonic frequency tracking application.
Forward-backward statistical linearized sigma-point Kalman smoother (FBSL-SPKS), which is recently proposed in [18], presents a new formulation for nonlinear smoothing using Sigma-Point Kalman filtering method. The derivation of the FBSL-SPKS is obtained by making use of the relationship between the SPKF and weighted statistical linear regression (WSLR). WSLR takes into account both the mean and covariance of the prior distribution to pseudolinearize the nonlinear dynamics. Therefore, it is more accurate than the first-order Taylor series-based linearization approach, which completely neglects the prior covariance at the point of linearization. In [18], the FBSL-SPKS is shown to obtain superior estimates than the EKS in general. To our best knowledge, however, the head-to-head performance comparison between the EKS and SPKS has not been made explicitly for the multiharmonic frequency tracking application. Especially, FBSL-SPKS has never been applied to any practical applications such as multiharmonic frequency tracking.
The first objective of our study was to implement two multiharmonic frequency trackers utilizing the EKS and FBSL-SPKS and demonstrate their feasibility of tracking the frequency of multiharmonic signals. The second objective was to compare the performance of the EKS and FBSL-SPKS trackers based on the Monte Carlo simulations and real biomedical signals. We used three performance metrics to quantify different aspects of the multiharmonic tracking performance. We only examined the smoothers since our work was focused on an offline analysis of prerecorded signals.
2. Methodology
We apply two nonlinear smoothing schemes using the EKF and SPKF approaches for multiharmonic frequency tracking problem. The EKF-based smoother, that is, the EKS, has many mathematically equivalent expressions. Here, we use a variant similar to that developed in [19] (see [20, page 374]). The nonlinear SPKF-based smoother was derived from the first principle in [18] and is referred as the FBSL-SPKS. The FBSL-SPKS is a fixed interval smoother, which uses two independent forward and backward filters for smoothing. The standard SPKF is used as a forward filter. The backward filter requires the inverse dynamics of the forward filter. While the EKS can easily invert the Taylor series based linearized dynamics, the SPKS requires a new approach to linearize the forward nonlinear dynamic model. There are two major variants of SPKS available in the literature which can solve this problem in a roundabout way. In [21], the inverse dynamic model was learned from the data by training a backward nonlinear predictor (e.g., neural network). The major disadvantages of this method are that it is application and data specific and requires a learning phase. Recently an Unscented Rauch-Tung-Striebel- (URTSS-) based smoother was proposed in [22], where a joint distribution of the current and future state is maintained in order to smoothen the current state. This method requires more computation due to doubling of the state dimension.
The FBSL-SPKS introduced a direct and straightforward formulation for forward-backward smoothing [18]. Instead of learning a backward dynamical model from the data, the proposed smoother (FBSL-SPKS) makes use of weighted statistical linear regression (WSLR) formulation of SPKF (see [18] for details). WSLR is a linearization technique that takes into account the uncertainty of the prior random variable when linearizing the nonlinear model. In this way, WSLR is more accurate in the statistical sense than the first-order Taylor series-based linearization employed by the EKF which only considers the mean of the prior densities while linearizing. By representing the forward nonlinear dynamics in terms of WSLR, a linear backward filter was derived from first principle in [18]. The forward and backward estimates were then statistically combined to obtain a smoothed estimate. This newly proposed FBSL-SPKS performed comparably with the smoothers presented in [21, 22] but with higher computational efficiency and ease of implementation.
2.1. State Space Model
We use boldface notation to denote random processes, normal face for deterministic parameters, upper case letters for matrices, lower case letters for vectors and scalars, and subscripts for time indices. The observed signal is denoted as  where
where  represent discrete time.
represent discrete time.
Our state space model is based on the one proposed in [4] with some modifications. The measurement model is based on a Fourier series representation in which the amplitudes, phases, and frequencies are allowed to change slowly over time. It can be expressed as

where  is the number of the harmonics assumed to be known,
is the number of the harmonics assumed to be known,  the instantaneous angle,
the instantaneous angle,  and
and  the amplitudes of the
the amplitudes of the  th harmonic sinusoidal components,
th harmonic sinusoidal components,  the trend of
the trend of  , and
, and  is a white noise process with zero-mean and variance
is a white noise process with zero-mean and variance  . The instantaneous angle
. The instantaneous angle  is modeled as
is modeled as

where  is the mean frequency,
is the mean frequency,  is the difference between the instantaneous frequency
is the difference between the instantaneous frequency  and the mean frequency
and the mean frequency  ,
,  the accumulative sum of
the accumulative sum of  , and
, and  the sample interval. This is one of the major differences between our state-space model and the one proposed in [4]. This modification was necessary because the FBSL-SPKS requires the state variables to have zero mean. Since
the sample interval. This is one of the major differences between our state-space model and the one proposed in [4]. This modification was necessary because the FBSL-SPKS requires the state variables to have zero mean. Since  is the accumulative sum of
is the accumulative sum of  , its mean is zero. This increases numerical stability and makes it easier to invert the model for the backward filter.
, its mean is zero. This increases numerical stability and makes it easier to invert the model for the backward filter.
Each state-space variable was modeled as follows:

where  is the fluctuating component in
is the fluctuating component in  ,
,  an autoregressive (AR) process coefficient of
an autoregressive (AR) process coefficient of  , and
, and  mutually uncorrelated white noise processes. A value of
mutually uncorrelated white noise processes. A value of  results in a random walk model of
results in a random walk model of  and
and  results in a white noise model. The variance
results in a white noise model. The variance  of
of  determines how quickly the parameters are expected to change over time.
determines how quickly the parameters are expected to change over time.
The state vector  is defined as
is defined as

Then, the state-space model can be written as follows:



where  and
and  are the linear state transition and nonlinear observation functions, respectively.
are the linear state transition and nonlinear observation functions, respectively.
2.2. EKS Frequency Tracker Recursions
2.2.1. Forward Updates
The filtered and predicted state estimates can be computed directly from the well-known EKF recursions, which can be found in [20]. In the recursions, the derivatives of the state transition function  and observation function
and observation function  have to be computed as part of time-update and measurement-update equations, respectively. They can be expressed as follows.
have to be computed as part of time-update and measurement-update equations, respectively. They can be expressed as follows.
-
(i)
Derivative of
 for time-update equations is
for time-update equations is (8)
(8) -
(ii)
Derivative of
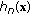 for measurement-update equations is
for measurement-update equations is (9)
(9)
The further detail of the EKF recursions can be found in [20].
2.2.2. Smoothing
There are many mathematically equivalent expressions for the extended Kalman smoother (EKS). Here we use a variant similar to that developed in [19] (see [20, page 374]). The backward recursive update equations for the EKS start with initialization at time  such as
such as

where  is called the adjoint variable. The smoothed estimates can then be computed as follows.
is called the adjoint variable. The smoothed estimates can then be computed as follows.
-
(i)
Backward-update equations are
 (11)
(11)
2.3. SPKS Multiharmonic Frequency Tracker Recursions
Our proposed FBSL-SPKS uses a forward-backward approach. A standard SPKF is run in the forward direction using the nonlinear model shown in (5) and (7). A backward filter then computes the estimates operating on the inverse dynamics of the forward filter. WSLR formulation as described below is used to pseudolinearize the nonlinear state-space model so that it is inverse can be computed. The forward and backward estimates are then optimally combined to generate the smoothed estimates. In order to better understand the equations of FBSL-SPKS, first we describe how SPKF performs an inherent linearization called WSLR, which considers both the mean and covariance of the prior random variable (RV) at the point of linearization.
-
(ii)
Weighted Statistical Linear Regression (WSLR) is as follows.
Consider a prior RV  which is propagated through a nonlinear function
which is propagated through a nonlinear function  to obtain a posterior RV
to obtain a posterior RV  . Sigma-points
. Sigma-points  are selected as the prior mean
are selected as the prior mean  plus and minus the columns of the square root of the prior covariance
plus and minus the columns of the square root of the prior covariance  :
:

where  is the RV dimension and
is the RV dimension and  is the composite scaling parameter. The sigma-points set
is the composite scaling parameter. The sigma-points set  completely captures the mean
completely captures the mean  and the covariance
and the covariance  of the prior RV
of the prior RV  :
:

where  is the normalized scaler weight for each sigma-point. Each prior sigma-point is propagated through the nonlinearity to form the posterior sigma-points set
is the normalized scaler weight for each sigma-point. Each prior sigma-point is propagated through the nonlinearity to form the posterior sigma-points set  :
:

The posterior statistics can then be calculated using weighted averaging of the posterior sigma-points,

An alternate view is to consider the estimates arising from the sigma-point approach as a weighted statistical linearization of the nonlinear dynamics:

where  and
and  are the statistical linearization parameters and can be determined by minimizing the expected mean square error which takes into account the uncertainty of the prior RV
are the statistical linearization parameters and can be determined by minimizing the expected mean square error which takes into account the uncertainty of the prior RV  . Defining
. Defining  is the expected mean square error with sigma-point weighting matrix
is the expected mean square error with sigma-point weighting matrix  :
:

The true expectation can be replaced as a finite sample approximation:

where the point wise linearization error is  . Now taking partial derivative on
. Now taking partial derivative on  with respect to
with respect to  we obtain
we obtain

By substituting  with
with  the equation can be rewritten as follows:
the equation can be rewritten as follows:

After cross multiplication and differentiation, (20) simplifies to

Solving for  from (21) we get
from (21) we get

Substituting the value of  obtained in (22) into
obtained in (22) into  and taking the partial derivative with respect to
and taking the partial derivative with respect to  we get
we get

Then, the equation can be rewritten as

Cross multiplication and differentiation with respect to  on (24) provides
on (24) provides

where  ; solving for
; solving for  from (25) we get
from (25) we get

where the prior mean ( ) and covariance (
) and covariance ( ) are calculated in (13) from the prior sigma-points. Similarly, the posterior mean (
) are calculated in (13) from the prior sigma-points. Similarly, the posterior mean ( ) and covariances (
) and covariances ( and
and  ) are calculated from the posterior sigma-points. The linearization error
) are calculated from the posterior sigma-points. The linearization error  has zero mean and covariance
has zero mean and covariance  which is defined as follows
which is defined as follows

Replacing  from(26)
from(26)

From (28),  , we observe that the covariance of the linearization error
, we observe that the covariance of the linearization error  is added when calculating the posterior covariance
is added when calculating the posterior covariance  . The uncertainty feedback scheme is very important especially when there is severe nonlinearity over the uncertainty region of prior RV. First-order Taylor series-based linearization employed by EKF often diverges in highly nonlinear region as it only performs linearization around the mean of the RV but neglects this error term. In general, the WSLR technique is an optimal way of linearizing any nonlinear function in the minimum mean square error (MMSE) sense as this approach explicitly takes into account the prior RV statistics (e.g., mean and covariance).
. The uncertainty feedback scheme is very important especially when there is severe nonlinearity over the uncertainty region of prior RV. First-order Taylor series-based linearization employed by EKF often diverges in highly nonlinear region as it only performs linearization around the mean of the RV but neglects this error term. In general, the WSLR technique is an optimal way of linearizing any nonlinear function in the minimum mean square error (MMSE) sense as this approach explicitly takes into account the prior RV statistics (e.g., mean and covariance).
To form the SPKF estimator, we consider the nonlinear state-space model:

where  is the state,
is the state,  is the observation at time index
is the observation at time index  ,
,  and
and  are Gaussian distributed process and observation noises,
are Gaussian distributed process and observation noises,  is the nonlinear dynamic model and
is the nonlinear dynamic model and  is the nonlinear observation model function. The process and observation noise has zero mean and covariances
is the nonlinear observation model function. The process and observation noise has zero mean and covariances  and
and  , respectively. The SPKF is then derived by recursively applying the sigma-point selection scheme shown above at every time index to these dynamic equations (see [13] for more details).
, respectively. The SPKF is then derived by recursively applying the sigma-point selection scheme shown above at every time index to these dynamic equations (see [13] for more details).
Alternatively, we may form the statistically linearized state-space using the WSLR technique:

where  ,
,  ,
,  , and
, and  are the statistical linearization parameters and
are the statistical linearization parameters and  ,
,  are the linearization error with mean zero and covariance
are the linearization error with mean zero and covariance  and
and  . All the parameters can be obtained by applying (22) and (26) iteratively at each time index
. All the parameters can be obtained by applying (22) and (26) iteratively at each time index  . Deriving the KF using the linearized state-space shown in (30) also leads to SPKF (see [21]). This statistically linearized form allows to form the dynamics of the backward filter used in forward-backward smoothing approach. As the statistically linearized state space shown in (30) is different from the standard linear state space used by the Kalman filter, the detailed derivation of the FBSL-SPKS which is demonstrated in the next sections needs to be done from the first principle. The pseudocode for the FBSL-SPKS can now be specified as follows.
. Deriving the KF using the linearized state-space shown in (30) also leads to SPKF (see [21]). This statistically linearized form allows to form the dynamics of the backward filter used in forward-backward smoothing approach. As the statistically linearized state space shown in (30) is different from the standard linear state space used by the Kalman filter, the detailed derivation of the FBSL-SPKS which is demonstrated in the next sections needs to be done from the first principle. The pseudocode for the FBSL-SPKS can now be specified as follows.
2.3.1. Forward Updates
A standard SPKF is used as the forward filter. The task of the SPKF is to estimate  at time index
at time index  given all past and current measurements. The SPKF recursions, which operates on the nonlinear state-space model defined in (29), are written below with WSLR.
given all past and current measurements. The SPKF recursions, which operates on the nonlinear state-space model defined in (29), are written below with WSLR.
-
(i)
Initialization:
 (31)
(31) -
(ii)
Calculation of sigma-points:
 (32)
(32)where
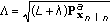 .
. -
(iii)
Time-update equations:
 (33)
(33) -
(iv)
Weighted Statistical Linearization of
 (
( ):
): (34)
(34) -
(v)
Measurement-update equations:
 (35)
(35) -
(vi)
Weighted Statistical Linearization of
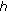 (
( ):
): (36)
(36) -
(vii)
where
 (37)
(37) -
(viii)
Parameters:
 is the composite scaling parameter which is given by
is the composite scaling parameter which is given by (38)
(38)where
 and
and  are the scaler sigma-point weights and they are defined as
are the scaler sigma-point weights and they are defined as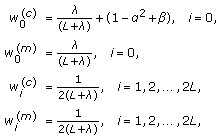 (39)
(39)
where  controls the size of the sigma-point distribution and should be within
controls the size of the sigma-point distribution and should be within  to avoid sampling nonlocal points when the nonlinearities are strong [21].
to avoid sampling nonlocal points when the nonlinearities are strong [21].  is the weighting term which incorporates the higher-order moments of the prior distribution. As generally sigma-points can effectively capture the first 2 moments (mean and covariance) of the distribution (for gaussian any symmetrical sigma-points set also capture the third-order moment, i.e., skewness), the parameter
is the weighting term which incorporates the higher-order moments of the prior distribution. As generally sigma-points can effectively capture the first 2 moments (mean and covariance) of the distribution (for gaussian any symmetrical sigma-points set also capture the third-order moment, i.e., skewness), the parameter  also can be used to minimize the error of higher-order moments of the distribution due to sigma-point approximation effects. For Gaussian prior,
also can be used to minimize the error of higher-order moments of the distribution due to sigma-point approximation effects. For Gaussian prior,  [13]. The parameter
[13]. The parameter  is used to make sure that the positive definiteness of the covariance matrices and the default choice of
is used to make sure that the positive definiteness of the covariance matrices and the default choice of  should work for most of the cases.
should work for most of the cases.  is the dimension of the augmented state;
is the dimension of the augmented state;  and
and  are the process and observation noise covariances.
are the process and observation noise covariances.
2.3.2. Backward Updates
An information filter is used to estimate the states from the backward direction given all the present and future measurements. As the statistically linearized state-space is different from the standard linear state-space used by the Kalman filter, the time and measurement update equations had to be derived from the first principle [18]. The backward filter recursion which operates on the statistically linearized state-space shown in (30) is given as fpllows.
-
(i)
Initializations:
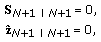 (40)
(40)where
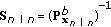 is the information matrix and
is the information matrix and 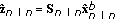 is defined as the information state. The state estimate and error covariance matrix for the backward filter can be denoted as
is defined as the information state. The state estimate and error covariance matrix for the backward filter can be denoted as  and
and  , respectively.
, respectively. -
(ii)
Time-update equations:
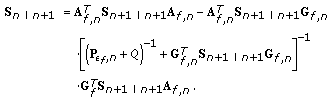 (41)
(41)Define
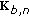 as the backward gain matrix:
as the backward gain matrix: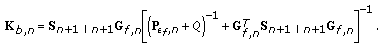 (42)
(42)Then,
 (43)
(43) -
(iii)
Measurement-update equations:
 (44)
(44)
2.3.3. Smoothing
The SPKF is run in the forward direction on the interval  to compute the forward posterior estimates
to compute the forward posterior estimates  . The information filter is then run backwards to form the prior backward estimates
. The information filter is then run backwards to form the prior backward estimates  . The two estimates are then optimally combined to obtain the smoothed estimate
. The two estimates are then optimally combined to obtain the smoothed estimate  and corresponding covariance
and corresponding covariance  .
.

3. Experiment
3.1. Synthetic Time-Variant Harmonic Signals
We generated two sets of synthetic signals with time-variant harmonics whose sample rate was  kHz, mean frequency
kHz, mean frequency  Hz, and duration
Hz, and duration  s using (1)–(3). The first set of synthetic signals contains the rhythmicity during the entire 3 seconds duration. The second set of synthetic signals contains the rhythmicity only during the first and last one seconds,
s using (1)–(3). The first set of synthetic signals contains the rhythmicity during the entire 3 seconds duration. The second set of synthetic signals contains the rhythmicity only during the first and last one seconds,  -
- and
and  -
- seconds. Between
seconds. Between  and
and  seconds the signals are simply white Gaussian noise. The second set of synthetic signals mimics those signals whose rhythmicity is intermittent.
seconds the signals are simply white Gaussian noise. The second set of synthetic signals mimics those signals whose rhythmicity is intermittent.
3.2. Parameter Selection
Tables 1 and 2 list the user-specified parameters that we used for the results and examples in this paper. In [17] we demonstrated that the ratio ( ) between the measurement noise variance and process noise variance is the critical factor that affects the performance of the EKS frequency tracker. We used the same value for the ratio (
) between the measurement noise variance and process noise variance is the critical factor that affects the performance of the EKS frequency tracker. We used the same value for the ratio ( ), which was
), which was  . The other values such as
. The other values such as  and
and  were selected based on empirical results obtained during the development of the multiharmonic frequency trackers. The user-specified parameters were chosen for the best performance of the EKS tracker [17]. We did not perform any additional tuning process for the SPKS tracker. Therefore, any bias incurred during the selection of the user-specified parameters would favor the EKS tracker.
were selected based on empirical results obtained during the development of the multiharmonic frequency trackers. The user-specified parameters were chosen for the best performance of the EKS tracker [17]. We did not perform any additional tuning process for the SPKS tracker. Therefore, any bias incurred during the selection of the user-specified parameters would favor the EKS tracker.
The SPKS multiharmonic frequency tracker has a few of parameters that the EKS tracker does not have. Those parameters and their chosen values are described in Section 2.3.1.
3.3. Performance Measures
There are two main issues that need to be addressed when comparing the performance of frequency trackers: accuracy and lock-on time. The accuracy quantifies how closely the tracker estimates the state. The lock-on time is a measure of how quickly the tracker can converge to the true state.
Depending on the application, the primary objective of frequency tracking may be accurate tracking of an instantaneous frequency or "signal denoising". When the rhythmicity in a given signal is intermittent, it is also important that the frequency tracker can regain its track of the intermittent instantaneous frequency as quickly as possible [10].
We used three metrics to compare the accuracy and speed of the EKS and FBSL-SPKS multiharmonic frequency trackers. The first metric is the normalized mean-square-error (NMSE):

where  is the signal duration.
is the signal duration.
The second metric is normalized frequency mean-square-error (NFMSE):

where  is the instantaneous frequency (IF),
is the instantaneous frequency (IF),  is the estimated IF, and
is the estimated IF, and  is the mean IF. NFMSE has a natural scale ranging from
is the mean IF. NFMSE has a natural scale ranging from  to
to  . A value
. A value  means that the average accuracy of the estimated IF is no better than simply using the mean IF as an estimate. Values of
means that the average accuracy of the estimated IF is no better than simply using the mean IF as an estimate. Values of  indicate poorer frequency tracking than a simple mean estimator and those of
indicate poorer frequency tracking than a simple mean estimator and those of  indicate accurate frequency tracking.
indicate accurate frequency tracking.
The third metric is the square-frequency-error ( ), which can be written as
), which can be written as

When this metric is averaged over an ensemble of synthetic signals, it visualizes how rapidly the trackers lock on to the true frequency. In contrast to NMSE and NFMSE,  is a function of time that shows the squared difference between the true IF and its estimate at a given time. For all of our results we calculated the NFMSE, NMSE, and SFE
is a function of time that shows the squared difference between the true IF and its estimate at a given time. For all of our results we calculated the NFMSE, NMSE, and SFE over an ensemble of
over an ensemble of  synthetic signals.
synthetic signals.
4. Results and Discussion
4.1. Synthetic Signals
Two plots in Figure 1 show the estimated multiharmonic frequencies using the EKS (a) and FBSL-SPKS (b) trackers on top of the spectrogram of a synthetic signal generated using (1)–(3) whose SNR was  dB. At
dB. At  s the EKS tracker lost track of the true frequency because the estimated third harmonic started tracking the fourth harmonic of the signal. The same situation occurred toward to the end of the signal at
s the EKS tracker lost track of the true frequency because the estimated third harmonic started tracking the fourth harmonic of the signal. The same situation occurred toward to the end of the signal at  s. However, the FBSL-SPKS tracker never lost its track of the true IT during the entire signal duration. Two plots in Figure 2 show the spectrograms of estimation residuals using the EKS (a) and FBSL-SPKS (b) trackers. The residual spectrogram (a) in Figure 2 depicts some harmonic structures between 1.1–1.7 s and 2.7–3.0 s due to the estimation error of the EKS tracker.
s. However, the FBSL-SPKS tracker never lost its track of the true IT during the entire signal duration. Two plots in Figure 2 show the spectrograms of estimation residuals using the EKS (a) and FBSL-SPKS (b) trackers. The residual spectrogram (a) in Figure 2 depicts some harmonic structures between 1.1–1.7 s and 2.7–3.0 s due to the estimation error of the EKS tracker.
(a) EKS Frequency Estimate and (b) FBSL-SPKS Frequency Estimate. The black area in the spectrograms represents great power concentrated in the corresponding frequency at a given time.Spectrogram of a true signal with the estimated harmonics (white lines) using the EKS frequency trackerSpectrogram of a true signal with the estimated harmonics (white lines) using the FBSL-SPKS frequency tracker
(a) EKS Estimation Error ( ) and (b) FBSL-SPKS Estimation Error (
) and (b) FBSL-SPKS Estimation Error ( ). The black area in the spectrograms represents great power concentrated in the corresponding frequency at a given time. If the harmonic tracking is successful, the black stripes in Figures 1(a) and 1(b) should be eliminated as shown in Figures 2(a) and 2(b). The EKS harmonic tracker does not track the harmonic components appropriately in the rectangular box in Figure 1(a), which results in the black stripes left in the box as shown in Figure 2(a).Spectrogram of residuals with the EKS frequency trackerSpectrogram of residuals with the FBSL-SPKS frequency tracker
). The black area in the spectrograms represents great power concentrated in the corresponding frequency at a given time. If the harmonic tracking is successful, the black stripes in Figures 1(a) and 1(b) should be eliminated as shown in Figures 2(a) and 2(b). The EKS harmonic tracker does not track the harmonic components appropriately in the rectangular box in Figure 1(a), which results in the black stripes left in the box as shown in Figure 2(a).Spectrogram of residuals with the EKS frequency trackerSpectrogram of residuals with the FBSL-SPKS frequency tracker
Figure 3(a) shows NMSE versus SNR of the EKS and FBSL-SPKS trackers. It demonstrates that the FBSL-SPKS tracker can estimate the true signal better than the EKS tracker over a wide range of SNR. Figure 3(b) depicts NFMSE versus SNR of two multiharmonic trackers. The FBSL-SPKS tracker outperformed the EKS tracker over the entire range of SNR. The performance difference is larger at low SNR values. This is probably due to a better approximation of the state and error covariances with the sampling approach of the FBSL-SPKS as compared to the local linearization approach of the EKS.
Figure 4 depicts the  of the two multiharmonic trackers. It demonstrates that on average the FBSL-SPKS tracker can regain its track of the true IF faster than the EKS tracker.
of the two multiharmonic trackers. It demonstrates that on average the FBSL-SPKS tracker can regain its track of the true IF faster than the EKS tracker.
Plots in Figure 5 show the estimated instantaneous frequencies using the EKS and FBSL-SPKS trackers on top of the spectrogram of a synthetic signal whose rhythmicity is present only during  -
- s and
s and  -
- s. The FBSL-SPKS tracker started tracking the true IF accurately at
s. The FBSL-SPKS tracker started tracking the true IF accurately at  s while the EKS frequency tracker failed to regain its track of the true IF. Plots in Figure 6 show the spectrograms of estimation residuals using the EKS Figure 6(a) and FBSL-SPKS Figure 6(b) trackers. The EKS tracker barely started tracking the true frequency toward the very end of the signal. However it took only
s while the EKS frequency tracker failed to regain its track of the true IF. Plots in Figure 6 show the spectrograms of estimation residuals using the EKS Figure 6(a) and FBSL-SPKS Figure 6(b) trackers. The EKS tracker barely started tracking the true frequency toward the very end of the signal. However it took only  seconds for the FBSL-SPKS to start tracking the true frequency after the rhythmicity came back at
seconds for the FBSL-SPKS to start tracking the true frequency after the rhythmicity came back at  seconds.
seconds.
4.2. Real Signal Examples
We applied both trackers to two different types of real signals: a photosenor insect activity signal and an arterial blood pressure (ABP) signal. The photosensor insect activity signal has a clear harmonic structure, which carries important entomological information. The instantaneous frequency and the harmonic amplitudes help entomologists determine what kind of insects flew over the photosensor [23, 24]. The ABP signal also has many harmonics by nature. Accurate tracking of the harmonics in the ABP signal is critical to check a patient's heart condition. However, the ABP signal can often be noisy due to signal drops and medical device interference. The following example will demonstrate that the FBSL-SPKS harmonic tracker is more robust to this type of noise than the EKS harmonic tracker.
The sampling frequency of the photosensor insect activity signal was  kHz and its duration was
kHz and its duration was  s. Figures 7(a) and 7(b) show the estimated harmonics using the EKS (a) and FBSL-SPKS (b) multiharmonic trackers on top of the spectrogram of a photosensor insect activity signal. Figures 8(a) and 8(b) are the spectrograms of estimation residuals using the EKS and FBSL-SPKS, respectively. The NMSE between the true and reconstructed bug signals using the FBSL-SPKS was
s. Figures 7(a) and 7(b) show the estimated harmonics using the EKS (a) and FBSL-SPKS (b) multiharmonic trackers on top of the spectrogram of a photosensor insect activity signal. Figures 8(a) and 8(b) are the spectrograms of estimation residuals using the EKS and FBSL-SPKS, respectively. The NMSE between the true and reconstructed bug signals using the FBSL-SPKS was  while that using the EKS was
while that using the EKS was  . The FBSL-SPKS tracker could track the harmonics during the entire time period while the EKS tracker lost its track between 2.3 s and 2.9 s, which is marked with two dark grey bars. The performance difference may not be apparent in Figures 8(a) and 8(b). However, the estimated harmonic frequencies between two grey bars in Figure 7(a) show that the slight error in fundamental frequency estimation results in the complete mismatch of higher harmonic frequency estimation. This result matches the simulation results shown in Figure 3.
. The FBSL-SPKS tracker could track the harmonics during the entire time period while the EKS tracker lost its track between 2.3 s and 2.9 s, which is marked with two dark grey bars. The performance difference may not be apparent in Figures 8(a) and 8(b). However, the estimated harmonic frequencies between two grey bars in Figure 7(a) show that the slight error in fundamental frequency estimation results in the complete mismatch of higher harmonic frequency estimation. This result matches the simulation results shown in Figure 3.
The ABP signal was sampled at  Hz and its duration was 30 minutes. Figures 9(a) and 9(b) depict the estimated harmonics using the EKS (a) and FBSL-SPKS (b) multiharmonic trackers on top of the spectrogram of an arterial blood pressure (ABP) signal. Figures 10(a) and 10(b) are the spectrograms of estimation residuals using the EKS and FBSL-SPKS trackers, respectively. Figure 9 shows a typical example of signal drops at 25 minutes, which is common in ABP signals. While the EKS tracker could not regain its track of the right frequencies after this signal drop, the FBSL-SPKS tracker was able to regain its track. This result again demonstrated that the FBSL-SPKS harmonic tracker is more reliable than the EKS harmonic tracker.
Hz and its duration was 30 minutes. Figures 9(a) and 9(b) depict the estimated harmonics using the EKS (a) and FBSL-SPKS (b) multiharmonic trackers on top of the spectrogram of an arterial blood pressure (ABP) signal. Figures 10(a) and 10(b) are the spectrograms of estimation residuals using the EKS and FBSL-SPKS trackers, respectively. Figure 9 shows a typical example of signal drops at 25 minutes, which is common in ABP signals. While the EKS tracker could not regain its track of the right frequencies after this signal drop, the FBSL-SPKS tracker was able to regain its track. This result again demonstrated that the FBSL-SPKS harmonic tracker is more reliable than the EKS harmonic tracker.
5. Conclusion
We implemented the multiharmonic tracker using the recently proposed FBSL-SPKS technique and made the head-to-head performance comparison between the FBSL-SPKS and EKS multiharmonic trackers based on synthetic and real-world signals. Using three difference performance metrics, we demonstrated that the FBSL-SPKS multiharmonic tracker is more accurate and robust to noise than the EKS multiharmonic tracker.
References
McAulary RJ, Quatieri TF: Speech analysis/synthesis based on a sinusoidal representation. IEEE Transactions on Acoustics, Speech, and Signal Processing 1986, 34(4):744-754. 10.1109/TASSP.1986.1164910
Tabrikian J, Dubnov S, Dickalov Y: Maximum a-posteriori probability pitch tracking in noisy environments using harmonic model. IEEE Transactions on Speech and Audio Processing 2004, 12(1):76-87. 10.1109/TSA.2003.819950
Li D, Jung R: Tracking rhythmicity in nonstationary quasi-periodic biomedical signals using adaptive time-varying covariance. Computers in Biology and Medicine 2002, 32(4):261-282. 10.1016/S0010-4825(02)00022-7
Parker PJ, Anderson BDO: Frequency tracking of nonsinusoidal periodic signals in noise. Signal Processing 1990, 20(2):127-152. 10.1016/0165-1684(90)90124-H
James B, Anderson BDO, Williamson RC: Conditional mean and maximum likelihood approaches to multiharmonic frequency estimation. IEEE Transactions on Signal Processing 1994, 42(6):1366-1375. 10.1109/78.286953
La Scala BF, Bitmead RR, Quinn BG: An exteded Kalman filter frequency tracker for high-noise environments. IEEE Transactions on Signal Processing 1996, 44(2):431-434. 10.1109/78.485940
La Scala BF, Bitmead RR: Design of an extended Kalman filter frequency tracker. IEEE Transactions on Signal Processing 1996, 44(3):739-742. 10.1109/78.489052
Bittanti S, Savaresi SM: On the parameterization and design of an extended Kalman filter frequency tracker. IEEE Transactions on Automatic Control 2000, 45(9):1718-1724. 10.1109/9.880631
Johnston LA, Krishnamurthy V: Derivation of a sawtooth iterated extended Kalman smoother via the AECM algorithm. IEEE Transactions on Signal Processing 2001, 49(9):1899-1909. 10.1109/78.942619
Fischler E, Bobrovsky BZ: Mean time to loose lock of phase tracking by particle filtering. Signal Processing 2006, 86(11):3481-3485. 10.1016/j.sigpro.2006.06.001
Dubois C, Davy M: Joint detection and tracking of time-varying harmonic components: a flexible bayesian approach. IEEE Transactions on Audio, Speech and Language Processing 2007, 15(4):1283-1295.
Kalman RE: A new approach to linear filtering and prediction problems. Transactions of the ASME 1960, 82: 35-45.
Julier SJ, Uhlmann JK: Unscented filtering and nonlinear estimation. Proceedings of the IEEE 2004, 92(3):401-422. 10.1109/JPROC.2003.823141
Norgaard M, Poulsen NK, Ravn O: New developments in state estimation for nonlinear systems. Automatica 2000, 36(11):1627-1638. 10.1016/S0005-1098(00)00089-3
van der Merwe R, Wan E: The square-root unscented kalman filter for state and parameter estimation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '01), May 2001 6: 3461-3464.
Kim S, McNames J: Tracking tremor frequency in spike trains using the extended Kalman filter. Proceedings of the Annual International Conference of the Engineering in Medicine and Biology Society, 2005 7: 7576-7579.
Kim S, McNames J: Tracking tremor frequency in spike trains using the extended Kalman smoother. IEEE Transactions on Biomedical Engineering 2006, 53(8):1569-1577. 10.1109/TBME.2006.877809
Paul AS, Wan EA: A new formulation for nonlinear forwardbackward smoothing. Proceedings of the IEEE International Conference on Acoustic Speech and Signal Processing (ICASSP '07), 2007
Bryson AE, Frazier M: Smoothing for linear and nonlinear dynamic systems. Aero Systems Division, Wright-Patterson Air Force Base, Dayton, Ohio, USA; 1963.
Kailath T, Sayed AH, Hassibi B: Linear Estimation. Prentice-Hall; 2000.
van der Merwe R: Sigma point kalman filters for probabilistic inference in dynamic state-space models, Ph.D. dissertation. OGI School of Science and Engineering, Oregon Health & Science University (OHSU); 2004.
Sarkka S: Unscented rauch-tung-striebel smoother. IEEE Transactions on Automatic Control 2008, 53(3):845-849.
Moore A, Miller J, Tabashnik B, Gage S: Automated identification of flying insects by analysis of wingbeat frequencies. Journal of Economic Entomology 1986, 79(6):1703-1706.
Moore A, Miller RH: Automated identification of optically sensed aphid (homoptera:aphidae) wingbeat waveforms. Annals of the Entomological Society of America 2002, 95(1):1-8. 10.1603/0013-8746(2002)095[0001:AIOOSA]2.0.CO;2
Acknowledgment
This work was supported in part by the Thrasher Research Fund.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, S., Paul, A.S., Wan, E.A. et al. Multiharmonic Frequency Tracking Method Using The Sigma-Point Kalman Smoother. EURASIP J. Adv. Signal Process. 2010, 467150 (2010). https://doi.org/10.1155/2010/467150
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/467150
 for time-update equations is
for time-update equations is
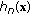 for measurement-update equations is
for measurement-update equations is



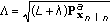 .
.
 (
( ):
):

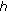 (
( ):
):

 is the composite scaling parameter which is given by
is the composite scaling parameter which is given by
 and
and  are the scaler sigma-point weights and they are defined as
are the scaler sigma-point weights and they are defined as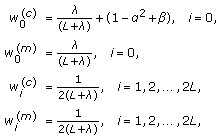
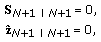
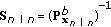 is the information matrix and
is the information matrix and 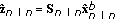 is defined as the information state. The state estimate and error covariance matrix for the backward filter can be denoted as
is defined as the information state. The state estimate and error covariance matrix for the backward filter can be denoted as  and
and  , respectively.
, respectively.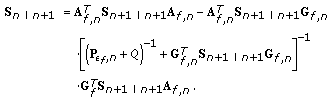
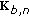 as the backward gain matrix:
as the backward gain matrix: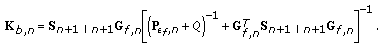






 versus Time) at
versus Time) at  . In this figure the shaded regions represent the 5th and 95th percentile ranges of the
. In this figure the shaded regions represent the 5th and 95th percentile ranges of the  .
.
 . (b) Estimated frequencies using the FBSL-SPKS on top of an intermittent rhythmicity signal at SNR = −3.EKS at SNR = −3FBSL-SPKS at SNR = −3
. (b) Estimated frequencies using the FBSL-SPKS on top of an intermittent rhythmicity signal at SNR = −3.EKS at SNR = −3FBSL-SPKS at SNR = −3



