- Research Article
- Open access
- Published:
Three-Dimensional Morphometry of Single Endothelial Cells with Substrate Stretching and Image-Based Finite Element Modeling
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 616091 (2009)
Abstract
Morphologically accurate reproduction of the behavior of endothelial cells is a key to understanding their mechanical behavior in cyclically inflated arteries and to quantitatively correlating this with cellular responses. We developed a novel technique to measure the three-dimensional geometry of cells on the substrate being stretched. We obtained sliced images of cells using confocal laser-scanning microscopy, and created image-based finite element models in the unloaded state assuming neo-Hookean material. Comparison of numerical predictions and experiments involving six cells when the substrate was stretched by 15% showed that the deformed geometry agreed with an average error of  0.55
0.55  m, roughly one-hundredth the size of a cell, for the lower half of the range of cellular height. Numerical sensitivity analyses showed that the cellular deformation under substrate stretching, that is, displacement boundaries, is insensitive to the absolute value of the elastic modulus, but depends on the nuclear to cytoplasmic modulus ratio.
m, roughly one-hundredth the size of a cell, for the lower half of the range of cellular height. Numerical sensitivity analyses showed that the cellular deformation under substrate stretching, that is, displacement boundaries, is insensitive to the absolute value of the elastic modulus, but depends on the nuclear to cytoplasmic modulus ratio.
1. Introduction
Arterial endothelial cells are exposed to periodic blood flow and undergo associated cyclic deformation. Their morphological changes and remodeling are mediated by these mechanical conditions. Therefore, it is important to determine the effects of the mechanical fields quantitatively by measuring the deformation of a cell, for example, with confocal laser-scanning microscopy (CLSM), and reproducing it accurately with a finite element model. Adequate modeling is a key to understand the mechanical behavior of a cell under substrate deformation and to correlate quantitatively the cellular and intracellular responses with mechanical factors.
The deformation of an adherent cell has been measured at the cellular or subcellular level after stretching the substrate or applying a force to the cell to identify the cell deformation behavior or force—displacement relationship [1]. The cellular and intracellular strains have been estimated in two dimensions on the horizontal plane perpendicular to the light axis of a microscope. To do so, one uses the relative displacement of fluorescent markers on the plasma membrane surface [2] and fluorescent [3] or nonfluorescent [4] markers in the cytoplasm, the correlation of cellular images captured as the fluorescence intensity texture on undeformed or deformed substrates [5, 6], or a comparison of the central cross-section of a cell (a chondrocyte in a gel) in CLSM images between the uncompressed and compressed states [7].
A hybrid technique for characterizing adherent cells combines mechanical measurement and finite element analysis [1, 8–10] as described below. For the three-dimensional (3D) modeling and stress analysis of cells subject to fluid shear stress, Ohashi et al. [8] measured the cellular free surface of bovine aortic endothelial cells in culture using an atomic force microscope, and Ferko et al. [10] measured the cytoplasm and nucleus in the same type of cell using total internal reflection fluorescence microscopy. They characterized the cell as an isotropic linear elastic material.
Hyperelastic material models have also been applied to improve the analysis of a cell undergoing large deformation. Caille et al. [1] modeled neo-Hookean material for a cell with Young's moduli (E) ranging from 100 to 2500 Pa and 500 to 25000 Pa for the cytoplasm and nucleus, respectively, compressed between parallel plates. Yamada et al. [11] and Yamada and Matsumura [12] modeled neo-Hookean material for a cell on a substrate being stretched with  Pa, 5100 Pa, and 775 kPa for the cytoplasm, nucleus, and substrate, respectively. Jean et al. [13] modeled neo-Hookean material to reproduce cell rounding behavior with
Pa, 5100 Pa, and 775 kPa for the cytoplasm, nucleus, and substrate, respectively. Jean et al. [13] modeled neo-Hookean material to reproduce cell rounding behavior with  Pa, 500–1500 Pa, 500 Pa, and 1000 Pa for the nucleus, cytoskeleton, cytosol, and cortical layer, respectively. Tracqui and Ohayon [14] used a second-order equation of the first invariant of the right Cauchy-Green deformation tensor for a cell body subjected to the rotation of embedded beads, and modeled neo-Hookean material with
Pa, 500–1500 Pa, 500 Pa, and 1000 Pa for the nucleus, cytoskeleton, cytosol, and cortical layer, respectively. Tracqui and Ohayon [14] used a second-order equation of the first invariant of the right Cauchy-Green deformation tensor for a cell body subjected to the rotation of embedded beads, and modeled neo-Hookean material with  Pa and 5100 Pa for the basal cell cortex and nucleus, respectively. However, the 3D geometry of an entire cell body in a theoretical model has never been compared to experimental measurements made under deformation.
Pa and 5100 Pa for the basal cell cortex and nucleus, respectively. However, the 3D geometry of an entire cell body in a theoretical model has never been compared to experimental measurements made under deformation.
Therefore, we examined the 3D deformation characteristics of cultured aortic endothelial cells under substrate stretching. We used CLSM to obtain the 3D geometry of cells on unstretched and uniaxially stretched substrate as a set of horizontally sliced images. Next we made a 3D finite element model of unstretched cells assuming incompressible isotropic hyperelastic material. Then we compared the 3D geometry of each measured stretched cell with the theoretical prediction based on a finite element analysis. We also evaluated the effects of the elasticity of intracellular components to obtain an accurate finite element analysis reproduction of cellular deformation due to substrate stretching.
2. Materials and Methods
2.1. Materials and Cell Culture
Porcine thoracic aortas obtained from a slaughterhouse were excised to remove endothelial cells [15]. The cells were dispersed in 35 mm dishes coated with type I collagen (Iwaki, Chiba, Japan) with D-MEM (Gibco, Grand Island, NY, USA) containing 10% fetal bovine serum (Gibco) and a 1% mixture of penicillin, streptomycin, and neomycin (Gibco). The cells were cultured in an incubator kept at 37°C in a 100% humidified atmosphere with 5% carbon dioxide. When the cells were 70%–80% confluent, they were detached with 0.05% trypsin–EDTA (Gibco) and subcultured in 35 mm tissue culture dishes (Iwaki).
The  mm bottom membrane in a silicone chamber (10-cc; Strex, Osaka, Japan) was coated with 1 mL 50
mm bottom membrane in a silicone chamber (10-cc; Strex, Osaka, Japan) was coated with 1 mL 50  g/mL fibronectin from porcine plasma (Wako Pure Chemical Industries, Osaka, Japan). Young's modulus of the membrane was 1267 kPa at room temperature. Cells from the second to fourth passages were transferred to the silicon membrane with 2 mL solution at a concentration of 25,600 cells/mL for seeding the cells at 5000 cells/cm2 to avoid cell-to-cell contact.
g/mL fibronectin from porcine plasma (Wako Pure Chemical Industries, Osaka, Japan). Young's modulus of the membrane was 1267 kPa at room temperature. Cells from the second to fourth passages were transferred to the silicon membrane with 2 mL solution at a concentration of 25,600 cells/mL for seeding the cells at 5000 cells/cm2 to avoid cell-to-cell contact.
2.2. Fluorescent Staining
After incubation overnight (13–16 hours), the cells were stained by replacing the culture medium (D-MEM) with 10  M calcein-AM (Dojindo, Kumamoto, Japan) and incubated for 30 minutes. Then the dish was rinsed once with D-PBS (Gibco) and filled with culture medium.
M calcein-AM (Dojindo, Kumamoto, Japan) and incubated for 30 minutes. Then the dish was rinsed once with D-PBS (Gibco) and filled with culture medium.
2.3. Image Acquisition of Unstretched and Stretched Cells
The chamber was mounted on the stretching apparatus of a microscopic stage (see Figure 1). The temperature of the bath was kept at 34–37°C by circulating hot water in the tube. An unstretched cell was scanned horizontally using CLSM (FV300-BX51WI; Olympus, Tokyo, Japan) with a 60  water immersion objective after adjusting the voltage of the photomultiplier tube so as to obtain brightness intensities within 256 levels. Then the following steps were repeated to obtain the 3D geometry of each cell.
water immersion objective after adjusting the voltage of the photomultiplier tube so as to obtain brightness intensities within 256 levels. Then the following steps were repeated to obtain the 3D geometry of each cell.
Experimental setup (a) with a silicone chamber (b). The right and left edges of the silicone chamber were grasped with a holding block and plate, and we inserted cylindrical pins into the four holes of the chamber to transmit a force from the connecting plates to the chamber. The chamber was stretched by moving the pair of pulse stages with a controller. The acrylic block kept the silicone membrane flat. A surfactant added to the water in the dish reduced the friction significantly between the acrylic block and the silicone membrane when stretching.
-
(1)
A cell in the unstretched state was scanned horizontally at 0.25-
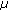 m height intervals over a height range of 20?
m height intervals over a height range of 20?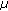 m using CLSM to acquire a series of fluorescent images (
m using CLSM to acquire a series of fluorescent images (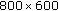 pixels, 0.167?
pixels, 0.167? m/pixel) within 3 minutes.
m/pixel) within 3 minutes. -
(2)
The silicone membrane was stretched for 30 seconds to a 15.1% strain at strain increments of 1.51% using a pair of pulse stages connected to a programmable controller (PS-30E-0 & CAT II; Chuo Precision Industrial, Tokyo, Japan). The focus of the cell was adjusted manually through a light microscope after each strain increment.
-
(3)
The cells were scanned between 1 and 4 minutes after reaching the applied strain. The scanning procedure was the same as that used for the unstretched state.
2.4. Compensation for Fading Fluorescence Intensity and Determination of the Intensity Threshold
We obtained equivalent thresholds of fluorescence intensity for the initial image scanned in the unstretched state and that scanned in the stretched state. As a pretest, cells were scanned in three dimensions using CLSM twice, 3 minutes apart. To determine the border of the cell body, excluding the very thin peripheral region, we chose a threshold, T1, as the level from which the intensity increased abruptly. The brightest  -pixel region in the image of the cell bottom was chosen in the first scan. Then the ratio of the mean intensity, r, was calculated by comparing the intensity in the second scan. The threshold in the second scan, T2, was assumed to be proportional to the ratio
-pixel region in the image of the cell bottom was chosen in the first scan. Then the ratio of the mean intensity, r, was calculated by comparing the intensity in the second scan. The threshold in the second scan, T2, was assumed to be proportional to the ratio  .
.
We scanned four cells using CLSM to validate the chosen threshold. Each cell was scanned horizontally at 0.25- m height intervals. Each cell was divided into bottom, middle, and top height regions. The bottom and middle regions were chosen at least 1
m height intervals. Each cell was divided into bottom, middle, and top height regions. The bottom and middle regions were chosen at least 1  m lower than the top of the cell. For example, if the height of the cell was 5.5
m lower than the top of the cell. For example, if the height of the cell was 5.5  m, the top and bottom images were obtained at heights of 5
m, the top and bottom images were obtained at heights of 5  m and 0
m and 0  m, respectively, and the middle images were obtained at heights of 1–4
m, respectively, and the middle images were obtained at heights of 1–4  m at 1-
m at 1- m intervals.
m intervals.
2.5. Image Processing
For unstretched cells, a candidate image of the cell bottom was chosen temporarily for each individual cell. Then a threshold value of the fluorescence intensity was obtained for a temporary cellular outline in which the intensity increased abruptly. A contour map was drawn for a series of sliced cell images using Igor Pro version 5 (WaveMetrics, Lake Oswego, OR, USA). The image that had the largest area surrounded by the outline was defined as the cell bottom because the substrate not stained with fluorescent markers was undetectable. Then the threshold of the cell was determined for that image.
Using the intensity threshold of the cell bottom, we redrew the contours for the other images at 1- m height intervals. From the average intensities of
m height intervals. From the average intensities of  -pixel squares in a cell region, we sought a peak value in the unstretched state and then calculated the corresponding average value in the same square in the stretched state, ignoring the deformation of the square of interest. The threshold value in the stretched state was calculated by taking the product of the threshold in the unstretched state and the average intensity in the stretched state divided by the average intensity in the unstretched state. A contour map was drawn for the cell in the stretched state using this threshold.
-pixel squares in a cell region, we sought a peak value in the unstretched state and then calculated the corresponding average value in the same square in the stretched state, ignoring the deformation of the square of interest. The threshold value in the stretched state was calculated by taking the product of the threshold in the unstretched state and the average intensity in the stretched state divided by the average intensity in the unstretched state. A contour map was drawn for the cell in the stretched state using this threshold.
2.6. Geometric Modeling and Finite Element Analysis
The coordinates of the points on the cellular outline were extracted manually to obtain a smooth outline for each image extending from the bottom to the top of the cell until the outline was difficult to identify due to the lack of staining in the top region. The coordinates of the outlines of the cell of interest were imported into Rhinoceros version 3 (Robert McNeel and Associates, Seattle, WA, USA). Closed curves were drawn using the points of cell outlines on the planes with a height interval of 1  m. Using the loft command, a free surface of the cell was constructed from a set of closed curves of cell outlines and an additional very small circle that was 0.5 or 1
m. Using the loft command, a free surface of the cell was constructed from a set of closed curves of cell outlines and an additional very small circle that was 0.5 or 1  m above the top slice. Then, a solid 3D model of the cell was reconstructed using the cap command and was connected to a plate of the substrate (
m above the top slice. Then, a solid 3D model of the cell was reconstructed using the cap command and was connected to a plate of the substrate (
 m) at the bottom of the cell. This solid model was imported into Abaqus/CAE (SIMULIA, Providence, RI, USA). The geometric model was partitioned into the two regions of cell and substrate, and the material properties in Table 1 were assigned to each of these. The model was meshed with 10-node tetrahedral hybrid elements (element type C3D10MH). The finite element analysis was carried out using Abaqus/Standard version 6.7 (SIMULIA).
m) at the bottom of the cell. This solid model was imported into Abaqus/CAE (SIMULIA, Providence, RI, USA). The geometric model was partitioned into the two regions of cell and substrate, and the material properties in Table 1 were assigned to each of these. The model was meshed with 10-node tetrahedral hybrid elements (element type C3D10MH). The finite element analysis was carried out using Abaqus/Standard version 6.7 (SIMULIA).
We postulated that the strain energy function of the neo-Hookean material was given by

where I1 is the first invariant of the right Cauchy-Green deformation tensor and C is the material constant, which is one-sixth of Young's modulus E for infinitesimal strains. The material constant C was defined as 129 Pa for a cell [1] and 211 kPa for the substrate (model  in Table 1).
in Table 1).
Displacements of  4.53
4.53  m (15.1% of the tensile strain) and
m (15.1% of the tensile strain) and  0.90
0.90  m (3.0% of the compressive strain) were applied to the sides of the substrate as boundary conditions. We obtained these strain values experimentally after all the image acquisitions were complete by averaging the relative displacements of four ink marks in a
m (3.0% of the compressive strain) were applied to the sides of the substrate as boundary conditions. We obtained these strain values experimentally after all the image acquisitions were complete by averaging the relative displacements of four ink marks in a  mm square while the silicone substrate was stretched. These marks were plotted at nine locations in a
mm square while the silicone substrate was stretched. These marks were plotted at nine locations in a  mm square at the center of the
mm square at the center of the  mm square membrane. The upper surface of the substrate (the cell bottom) was held at the same height to obtain the cellular deformation with respect to the substrate surface.
mm square membrane. The upper surface of the substrate (the cell bottom) was held at the same height to obtain the cellular deformation with respect to the substrate surface.
2.7. Error Estimation for Cell Outlines at Various Heights
The average error in the cellular outlines was estimated between the first and second pretest scans and between the experimental data and theoretical predictions. The error was calculated by adding all the areas surrounded by segments of the outline,  and dividing the sum by the perimeter of the shorter outline for the pretest scans or the perimeter of the theoretical model for the comparison between experimental and theoretical results (see Figure 2). Rigid body motion was removed by matching the cell bottom outline in an image of the stretched state to that obtained by applying the substrate deformation to the cell bottom outline for the unstretched state. For the finite element analysis results, the two-dimensional (2D) displacement was calculated for nodes at each height range in the unstretched state, that is,
and dividing the sum by the perimeter of the shorter outline for the pretest scans or the perimeter of the theoretical model for the comparison between experimental and theoretical results (see Figure 2). Rigid body motion was removed by matching the cell bottom outline in an image of the stretched state to that obtained by applying the substrate deformation to the cell bottom outline for the unstretched state. For the finite element analysis results, the two-dimensional (2D) displacement was calculated for nodes at each height range in the unstretched state, that is,  and
and  ,
,  neglecting the component in the height direction.
neglecting the component in the height direction.
2.8. Sensitivity of the Cellular Deformation to the Elasticity of Intracellular Components: A Numerical Study
We investigated the effects of the elasticity of the intracellular components numerically, focusing mainly on the cytoplasm and nucleus during the cell deformation. We prepared finite element models ( ) with the same geometry as model
) with the same geometry as model  and various material constant values corresponding to Young's moduli for the spread of endothelial cells reported by Caille et al. [1], to investigate the sensitivity of the cellular deformation to the elasticity of the cytoplasm and nucleus (see Table 1). The cytoplasm and nucleus were completely connected at their boundaries. We compared the deformation of the cellular free surface obtained using the above analyses.
and various material constant values corresponding to Young's moduli for the spread of endothelial cells reported by Caille et al. [1], to investigate the sensitivity of the cellular deformation to the elasticity of the cytoplasm and nucleus (see Table 1). The cytoplasm and nucleus were completely connected at their boundaries. We compared the deformation of the cellular free surface obtained using the above analyses.
The sensitivity to the amount of substrate stretching was also investigated for model  . With x and y denoted as the axes of stretching and the transverse directions, respectively, the substrate strains were varied as
. With x and y denoted as the axes of stretching and the transverse directions, respectively, the substrate strains were varied as  , and
, and 
3. Results
The ratio (r) of the mean intensity in the central  -pixel region in the second scan to that in the first scan was
-pixel region in the second scan to that in the first scan was  (
( ) for the bottom images of four cells. Table 2 summarizes the error estimates for the cell outlines that were identified by the T1 and T2 threshold values. The r-value was used to compensate for fluorescence fading in the latter. In the bottom and middle regions, the average error was 0.24 to 0.26
) for the bottom images of four cells. Table 2 summarizes the error estimates for the cell outlines that were identified by the T1 and T2 threshold values. The r-value was used to compensate for fluorescence fading in the latter. In the bottom and middle regions, the average error was 0.24 to 0.26  m, or less than one-hundredth of the cell size. The top region had a large average error of 0.44
m, or less than one-hundredth of the cell size. The top region had a large average error of 0.44  m, which was significantly different from the average values for the other regions (
m, which was significantly different from the average values for the other regions ( using a statistical t-test).
using a statistical t-test).
 ). The outline derived from the second measurement was compensated for fluorescent fading.
). The outline derived from the second measurement was compensated for fluorescent fading.Figure 3 shows an example set of fluorescence intensity images of an endothelial cell stained with calcein-AM. The images are located at heights of 5, 4, 3, 2, 1, and 0  m, where 0
m, where 0  m corresponds to the cell bottom. The intensity in the cell region tended to decrease at higher levels.
m corresponds to the cell bottom. The intensity in the cell region tended to decrease at higher levels.
Figure 4(a) shows an example of the fluorescence intensity contours at the cell bottom (right image in Figure 3(b)), and Figure 4(b) shows a side view of a surface plot of the intensity. Based on the results in Figure 4(b), the intensity threshold for identifying the cell outline was determined to be 55.
(a) Contours of the fluorescence intensity at the cell bottom (right image in Figure 3(b)). The thick contour corresponds to the threshold value 55. (b) A side view of the surface plot of the intensity was used to determine the threshold value of 55.
Figure 5 shows the geometries of typical finite element models of measured single cells on the substrate before and after stretching. In the geometrical modeling, a small circle was added to the top of the cell at a height of 0.5 or 1.0  m above the highest outline. For the substrate, the edges to the right and left of the figure were stretched by 15.1%, whereas those on the other sides were compressed by 3.0%. The distribution of the maximum principal strain during stretching was plotted on the surfaces of the cell and substrate (right panels in Figure 5).
m above the highest outline. For the substrate, the edges to the right and left of the figure were stretched by 15.1%, whereas those on the other sides were compressed by 3.0%. The distribution of the maximum principal strain during stretching was plotted on the surfaces of the cell and substrate (right panels in Figure 5).
Geometry of typical finite element models of a cell on the substrate before and after stretching. In the left panels, the substrate is 60- m-square before stretching. In the right panels, the distribution of the maximum principal strain is also shown for cells when the substrate is stretched in the horizontal direction by 15.1%. The cell in the top line is model
m-square before stretching. In the right panels, the distribution of the maximum principal strain is also shown for cells when the substrate is stretched in the horizontal direction by 15.1%. The cell in the top line is model  , and its profile is made from the images in Figure 3. The cell in the bottom line is model
, and its profile is made from the images in Figure 3. The cell in the bottom line is model  .
.
Table 3 shows the mean and SD of the nominal strain components in the stretching, transverse, and height directions at various height levels of the cell models in Figure 5. The strain components in the stretching and transverse directions were almost equal to the strain of the substrate at the cell bottom; the former strain component decreased gradually, whereas the latter remained relatively constant with increasing height. The strain component in the height direction was 11% compressive in the bottom region and decreased toward zero with increasing height.
 m in the unstretched state) and the lower cell model (height: 5.5
m in the unstretched state) and the lower cell model (height: 5.5  m in the unstretched state) in Figure 5, respectively. The substrate was deformed with strains of 15.1% in the stretching direction and
m in the unstretched state) in Figure 5, respectively. The substrate was deformed with strains of 15.1% in the stretching direction and  % in the transverse direction. Extrapolated values for element nodes from integration-point values were averaged over each height range.
% in the transverse direction. Extrapolated values for element nodes from integration-point values were averaged over each height range.Figure 6 compares (a) the contours measured in the unstretched state (blue lines) to those smoothed to make the 3D geometric models (red lines) and (b) the contours measured in the stretched state (blue lines) to the ones predicted by the finite element analysis (red lines). In the figure, the horizontal direction is the stretching direction, and the height interval of each contour is 1  m. The cell was elongated in the substrate-stretching direction, with an associated slight compression in the transverse direction.
m. The cell was elongated in the substrate-stretching direction, with an associated slight compression in the transverse direction.
Comparisons of (a) contours measured in the unstretched state (blue lines) and those smoothed to make the 3D geometric models (red lines), and (b) contours measured in the stretched state (blue lines) and those predicted by the finite element analysis (red lines). The height interval between adjacent outlines is 1  m. Bar: 20
m. Bar: 20  m.
m.
Table 4 summarizes the distance error between the outlines obtained from the measurements in the stretched state and those obtained from finite element analyses for six cells. In the third column, the relative error of the displacement is listed with respect to the mean 2D displacement of the cellular free surface at the same height level. For the lower half of the cells, the average distance error was 0.41 to 0.55  m, or 24% to 48% of the mean displacement at the same height level, whereas these values were 0.86 to 1.28
m, or 24% to 48% of the mean displacement at the same height level, whereas these values were 0.86 to 1.28  m or 128% to 278% for the upper half of the cells. Such large relative errors resulted from dividing the distance error by a small mean displacement which decreased toward zero with increasing height.
m or 128% to 278% for the upper half of the cells. Such large relative errors resulted from dividing the distance error by a small mean displacement which decreased toward zero with increasing height.
 ). At each height level for cells in the finite element analysis, the 2D mean displacement was calculated excluding the displacement component in the height direction.
). At each height level for cells in the finite element analysis, the 2D mean displacement was calculated excluding the displacement component in the height direction.Figures 7(a) and 7(b) compare the displacement in the height direction in the major and minor cross-sections between models  and
and  to illustrate the effect of nuclear elasticity, which was (a)
to illustrate the effect of nuclear elasticity, which was (a)  Pa and (b)
Pa and (b)  Pa. In Figure 7(a), the deformed model
Pa. In Figure 7(a), the deformed model  had two peak-displacement regions in the free-surface regions due to the stiff nucleus. In Figure 7(b), the deformed model
had two peak-displacement regions in the free-surface regions due to the stiff nucleus. In Figure 7(b), the deformed model  had almost horizontal isodisplacement lines, showing near uniform deformation at each height level. Figure 7(c) compares the displacement in the stretching direction in the major cross-section between models
had almost horizontal isodisplacement lines, showing near uniform deformation at each height level. Figure 7(c) compares the displacement in the stretching direction in the major cross-section between models  (top panel) and
(top panel) and  (bottom panel). The stiff nucleus restricted the deformations of itself and the cytoplasm in its vicinity, decreasing the height reduction of the cellular top and the nuclear elongation in the stretching direction when the substrate was stretched.
(bottom panel). The stiff nucleus restricted the deformations of itself and the cytoplasm in its vicinity, decreasing the height reduction of the cellular top and the nuclear elongation in the stretching direction when the substrate was stretched.
Comparisons of (a) the displacement in the height direction along the major and minor cross-sections for model  and (b) model
and (b) model  ; (c, top panel) displacement in the stretching direction along the major cross-section for model
; (c, top panel) displacement in the stretching direction along the major cross-section for model  and (c, bottom panel) model
and (c, bottom panel) model  under 15. 1% stretching of the substrate associated with 3.0% transverse compression. In the figure, the substrate is stretched symmetrically in the right and left directions.
under 15. 1% stretching of the substrate associated with 3.0% transverse compression. In the figure, the substrate is stretched symmetrically in the right and left directions.
The sensitivity of the deformation of the cellular free surface to the elasticity of the cytoplasm and nucleus was evaluated. The difference between the 2D displacement of nodes (height  0 in the unloaded state) on the cellular free surface in models
0 in the unloaded state) on the cellular free surface in models  and
and  was
was 
 m or
m or  % (mean
% (mean  SD) compared to the mean 2D displacement of these nodes. Among models
SD) compared to the mean 2D displacement of these nodes. Among models  , the maximum difference was
, the maximum difference was  m or
m or  % (
% ( versus
versus  ,
,  , or
, or  ; models
; models  ,
,  , and
, and  had identical displacements). These errors were smaller than the spatial resolution of the images.
had identical displacements). These errors were smaller than the spatial resolution of the images.
The sensitivity of the deformation of the cellular free surface to the magnitude of substrate stretching was also evaluated using model  . The difference between the substrate stretching and the mean 2D displacement of the nodes on the cellular free surface (height
. The difference between the substrate stretching and the mean 2D displacement of the nodes on the cellular free surface (height  0 in the unloaded state) was
0 in the unloaded state) was 
 m and
m and  % (mean
% (mean  SD) between
SD) between  and 0.101 with a constant
and 0.101 with a constant  , and
, and 
 m and
m and  % between
% between  and 0 with a constant
and 0 with a constant  .
.
4. Discussion
Published studies on the deformation of an entire cell typically analyzed cellular deformation independent of height position [2–6]. In confocal sectioning of chondrocytes, the outlines were compared between the uncompressed and compressed states only in the central plane of each cell [7]. Furthermore, in image-based 3D modeling of cells [8, 10, 16], the geometric change of an entire cell with the application of force or displacement that was seen in a numerical analysis was not compared with experimental results. By contrast, we obtained a contour map of cells in the unstretched and stretched states, enabling an analysis of the height-dependent deformation. Then, we compared the outline of cells on the substrate surface between the unstretched and stretched states, considering the deformation of the substrate. We also made finite element models and compared the theoretically predicted profiles with experimentally obtained outlines of cells at different heights. These techniques will lead to more accurate understanding of the three-dimensional deformation of cells subjected to various forces and displacements.
Experimental and theoretical analyses of cellular deformation indicate that a hyperelastic material model is a practical approximation for describing the deformation of a cell after quasistatic stretching after completion of the stress relaxation. A finite element model by Yamada et al. [17] consisting of a neo-Hookean plasma membrane and incompressible cytoplasm caused slight buckling of the cellular free surface under uniaxial stretching of the substrate. Solid constituents in the cytoplasm must be requisite to support the flexible plasma membrane. Our model expressed the cytoplasm as a neo-Hookean material, which is more appropriate for describing the cell deformation.
To determine the morphometry of each cell, we dyed the cytoplasm with calcein-AM and determined a threshold value to obtain the cell boundary. Peeters et al. [18] showed a continuous change in the fluorescence intensity at the boundary of a fluorescent bead. Thus, it is necessary to determine a threshold value for the cell boundary. We confirmed that well-determined thresholds in images before and after stretching indicate the same boundary. Although a threshold might define a larger or smaller region than the actual cell boundary, the cell body defined using the threshold is made of the same material.
There are fluorescent dyes that label the plasma membrane to identify a cell border. To the best of our knowledge, however, these have not been used for the purpose of extracting the 3D border from adherent cells. Such dyes might not be suitable for staining the fine details of all parts of the plasma membrane of adherent cells, both at the free surface and the cell bottom.
According to Table 4, our cell body model could be used to provide a practical reproduction of the cellular deformation, with possible small errors in the boundary for the lower half of the cell but significant errors for the upper half. This might have been due to a lack of volume with sufficient fluorescence intensity in the top region of a cell. By comparing the right image in Figure 3(b) and the contour labeled "55" in Figure 4(a), it is evident that lamellipodia and filopodia were not included in the 3D geometrical model. The volume of these podia was too small for the fluorescence intensity to be detected above the threshold.
A  -pixel region in the cell bottom image was theoretically deformed to a
-pixel region in the cell bottom image was theoretically deformed to a  -pixel region by the substrate deformation. Between these pixel regions, 70 pixels sharing 18% of the region were not identical. We ignored the error resulting from this difference because the
-pixel region by the substrate deformation. Between these pixel regions, 70 pixels sharing 18% of the region were not identical. We ignored the error resulting from this difference because the  -pixel region at the central portion of the cell bottom had a small fluorescence intensity gradient (see Figure 4). A complicated procedure would be required to determine the fluorescence fading rate between the unstretched and stretched states.
-pixel region at the central portion of the cell bottom had a small fluorescence intensity gradient (see Figure 4). A complicated procedure would be required to determine the fluorescence fading rate between the unstretched and stretched states.
The basic models in the present study (models  ) assumed a homogeneous material due to the lack of data on microscopic or regional material properties. A cell consists of various organelles, such as the nucleus and cytoskeleton. Of these organelles, the nucleus has the greatest effect on the cell deformation. The displacement of the free surface differed by
) assumed a homogeneous material due to the lack of data on microscopic or regional material properties. A cell consists of various organelles, such as the nucleus and cytoskeleton. Of these organelles, the nucleus has the greatest effect on the cell deformation. The displacement of the free surface differed by  0.1
0.1  m or 7% of the mean displacement of nodes from that of the nucleus-free model under substrate stretching. This difference is at most one-fifth of the error in the lower region of cells in the experiment (see Table 4).
m or 7% of the mean displacement of nodes from that of the nucleus-free model under substrate stretching. This difference is at most one-fifth of the error in the lower region of cells in the experiment (see Table 4).
In reality, an endothelial cell consists of viscoelastic material [19], and its mechanical properties change when it remodels [20]. No well-defined 3D viscoelastic material model has yet been established, and the remodeling process has not been incorporated into a constitutive or structural model, which remains as a future problem.
In the present study, we only applied displacement boundary conditions and assumed a simple nucleus geometry, referring to the finite element model in Caille et al. [1]. Force boundary conditions, such as cell poking, should be considered to validate the material properties in the finite element model. The geometry and location of the nucleus are also important factors to describe the mechanical states of intracellular components. Modeling of cells on the basis of double- or multistaining image data for the cytoplasm and nucleus, and considering stress fibers and focal adhesions, remain as areas of future study.
Prestress in the cytoskeletal network has been incorporated in the tensegrity model, which is a representative unit of the cytoplasm [16, 21]. So far, our finite element models represent homogenized behavior in the cytoplasm. Reproducing the microscopic stress distribution in cytoskeletal components is an area of future study that will also incorporate pretension in actin filaments.
5. Conclusion
This is the first study to measure and validate the 3D geometrical change of adherent cells when the substrate is stretched. The advantages of the 3D measurement and numerical deformation analysis are that they provide detailed data on the cellular deformation according to the height position, reflecting the cellular shape. We also analyzed the sensitivity of the elasticity of intracellular components on the cellular deformation. The present study provides a basis of adequate finite element modeling of cells under stretching of the vascular wall or substrate to investigate effects caused by the mechanical environment. Future studies should measure and model the cellular structure precisely and also reproduce the mechanical fields to correlate with intracellular responses such as stress fiber formation.
References
Caille N, Thoumine O, Tardy Y, Meister J-J: Contribution of the nucleus to the mechanical properties of endothelial cells. Journal of Biomechanics 2002, 35(2):177-187. 10.1016/S0021-9290(01)00201-9
Barbee KA, Macarak EJ, Thibault LE: Strain measurements in cultured vascular smooth muscle cells subjected to mechanical deformation. Annals of Biomedical Engineering 1994, 22(1):14-22. 10.1007/BF02368218
Caille N, Tardy Y, Meister J-J: Assessment of strain field in endothelial cells subjected to uniaxial deformation of their substrate. Annals of Biomedical Engineering 1998, 26(3):409-416.
Simon SI, Schmid-Schönbein GW: Cytoplasmic strains and strain rates in motile polymorphonuclear leukocytes. Biophysical Journal 1990, 58(2):319-332. 10.1016/S0006-3495(90)82379-1
Gilchrist CL, Witvoet-Braam SW, Guilak F, Setton LA: Measurement of intracellular strain on deformable substrates with texture correlation. Journal of Biomechanics 2007, 40(4):786-794. 10.1016/j.jbiomech.2006.03.013
Wall ME, Weinhold PS, Siu T, Brown TD, Banes AJ: Comparison of cellular strain with applied substrate strain in vitro. Journal of Biomechanics 2007, 40(1):173-181. 10.1016/j.jbiomech.2005.10.032
Lee DA, Knight MM, Bolton JF, Idowu BD, Kayser MV, Bader DL: Chondrocyte deformation within compressed agarose constructs at the cellular and sub-cellular levels. Journal of Biomechanics 2000, 33(1):81-95. 10.1016/S0021-9290(99)00160-8
Ohashi T, Sugawara H, Matsumoto T, Sato M: Surface topography measurement and intracellular stress analysis of cultured endothelial cells exposed to fluid shear stress. JSME International Journal, Series C 2000, 43(4):780-786.
Charras GT, Horton MA: Determination of cellular strains by combined atomic force microscopy and finite element modeling. Biophysical Journal 2002, 83(2):858-879. 10.1016/S0006-3495(02)75214-4
Ferko MC, Bhatnagar A, Garcia MB, Butler PJ: Finite-element analysis of a multicomponent model of sheared and focally adhered endothelial cells. Annals of Biomedical Engineering 2007, 35: 208-223. 10.1007/s10439-006-9223-4
Yamada H, Morita D, Matsumura J, Takemasa T, Yamaguchi T: Numerical simulation of stress fiber orientation in cultured endothelial cells under biaxial cyclic deformation using the strain limit hypothesis. JSME International Journal, Series C 2002, 45(4):880-888. 10.1299/jsmec.45.880
Yamada H, Matsumura J: Finite element analysis of the mechanical behavior of a vascular endothelial cell in culture under substrate stretch. Transactions of JSME, Series A 2004, 70(5):710-716.
Jean RP, Chen CS, Spector AA: Finite-element analysis of the adhesion-cytoskeleton-nucleus mechanotransduction pathway during endothelial cell rounding: axisymmetric model. Journal of Biomechanical Engineering 2005, 127(4):594-600. 10.1115/1.1933997
Tracqui P, Ohayon J: Transmission of mechanical stresses within the cytoskeleton of adherent cells: a theoretical analysis based on a multi-component cell model. Acta Biotheoretica 2004, 52(4):323-341.
Yamada H, Ando H: Orientation of apical and basal actin stress fibers in isolated and subconfluent endothelial cells as an early response to cyclic stretching. Molecular and Cellular Biomechanics 2007, 4(1):1-12.
Stamenovic D: Effects of cytoskeletal prestress on cell rheological behavior. Acta Biomaterialia 2005, 1(3):255-262. 10.1016/j.actbio.2005.01.004
Yamada H, Ishiguro H, Tamagawa M: Mechanical behavior and structural changes of cells subjected to mechanical stimuli: deformation, freezing, and shock waves. In Biomechanics at Micro- and Nanoscale Levels. Volume 1. Edited by: Wada H. World Scientific, Singapore; 2005:154-164.
Peeters EAG, Bouten CVC, Oomens CWJ, Bader DL, Snoeckx LHEH, Baaijens FPT: Anisotropic, three-dimensional deformation of single attached cells under compression. Annals of Biomedical Engineering 2004, 32(10):1443-1452.
Sato M, Ohshima N, Nerem RM: Viscoelastic properties of cultured porcine aortic endothelial cells exposed to shear stress. Journal of Biomechanics 1996, 29(4):461-467. 10.1016/0021-9290(95)00069-0
Nerem RM, Seliktar D: Vascular tissue engineering. Annual Review of Biomedical Engineering 2001, 3: 225-243. 10.1146/annurev.bioeng.3.1.225
Ingber DE: Tensegrity 1. Cell structure and hierarchical systems biology. Journal of Cell Science 2003, 116: 1157-1173. 10.1242/jcs.00359
Acknowledgment
This study was partially supported by a Grant-in-Aid for Scientific Research on Priority Areas (no. 15086213) from the Ministry of Education, Culture, Sports, Science, and Technology of Japan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yamada, H., Mouri, N. & Nobuhara, S. Three-Dimensional Morphometry of Single Endothelial Cells with Substrate Stretching and Image-Based Finite Element Modeling. EURASIP J. Adv. Signal Process. 2010, 616091 (2009). https://doi.org/10.1155/2010/616091
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/616091

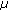 m height intervals over a height range of 20?
m height intervals over a height range of 20?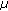 m using CLSM to acquire a series of fluorescent images (
m using CLSM to acquire a series of fluorescent images (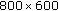 pixels, 0.167?
pixels, 0.167? m/pixel) within 3 minutes.
m/pixel) within 3 minutes.
 )/perimeter.
)/perimeter.

 m (b, left to right), where 0
m (b, left to right), where 0  m is the cell bottom. The cell was stained with calcein-AM. Bar: 20
m is the cell bottom. The cell was stained with calcein-AM. Bar: 20  m.
m.


