- Research Article
- Open access
- Published:
Joint Linear Processing for an Amplify-and-Forward MIMO Relay Channel with Imperfect Channel State Information
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 640186 (2010)
Abstract
The problem of jointly optimizing the source precoder, relay transceiver, and destination equalizer has been considered in this paper for a multiple-input-multiple-output (MIMO) amplify-and-forward (AF) relay channel, where the channel estimates of all links are assumed to be imperfect. The considered joint optimization problem is nonconvex and does not offer closed-form solutions. However, it has been shown that the optimization of one variable when others are fixed is a convex optimization problem which can be efficiently solved using interior-point algorithms. In this context, an iterative technique with the guaranteed convergence has been proposed for the AF MIMO relay channel that includes the direct link. It has been also shown that, for the double-hop relay case without the receive-side antenna correlations in each hop, the global optimality can be confirmed since the structures of the source precoder, relay transceiver, and destination equalizer have closed forms and the remaining joint power allocation can be solved using Geometric Programming (GP) technique under high signal-to-noise ratio (SNR) approximation. In the latter case, the performance of the iterative technique and the GP method has been compared with simulations to ensure that the iterative approach gives reasonably good solutions with an acceptable complexity. Moreover, simulation results verify the robustness of the proposed design when compared to the nonrobust design that assumes estimated channels as actual channels.
1. Introduction
The application of relays for cooperative communications has received a lot of interest in recent years. It is well known that the channel impairments such as shadowing, multipath fading, distance-dependent path losses, and interference often degrade the link quality between the source and destination in a wireless network. If the link quality degrades severely, relays can be employed between the source and destination nodes for assisting the transmission of data from the source to destination [1]. In the literature, various types of cooperative communications such as amplify-and-forward (AF), decode-and-forward [1], coded-cooperation [2], and compress-and-forward [3] have been presented. In [4], the outage and ergodic capacities have been analyzed for a three-node network where one of the nodes relays the messages of another node towards the third one. Among several cooperation schemes [1–4], the AF scheme is more attractive due to its simplicity since the relay simply forwards the signal and does not decode it. Recently, space-time coding strategies have been developed for relay networks [5]. In [6], the authors study distributed beamforming for a cooperative network which consists of a transmitter, a receiver, and an arbitrary number of relay nodes. The common things among aforementioned works are that the transmitter, receiver, and the relays are all single-antenna nodes and the channel state information (CSI) (either instantaneous or second-order statistics of the channel) is assumed to be error-free.
The performance of cooperative communications can be further enhanced by employing multiple-input-multiple-output (MIMO) relays [7]. The optimal designs of AF MIMO relays have been investigated in [8, 9] for point-to-point and in [10, 11] for point-to-multipoint communications assuming that the available CSI is perfect. The robust design of MIMO relay for multipoint-to-multipoint communications has been solved in [12], where the sources and destinations are single antenna nodes. The optimal design of multiple AF MIMO relays in a point-to-point communication scenario has been considered in [13, 14] to minimize the mean-square error (MSE) and satisfy the quality of service (QoS) requirements. These works also assume perfect knowledge of CSI. Recently, the joint robust design of AF MIMO relay and destination equalizer has been investigated in [15] for a double-hop (without direct link) MIMO relay channel. To the best source of our knowledge, the joint optimization of the source precoder, MIMO relay, and the destination equalizer has not been considered in the literature for the case where the CSI is imperfect and the direct link is included. Although the path attenuation for the direct link is much larger than that for the link via relay, due to the fading of the wireless channels, there can be still a significant number of instantaneous channels during which the direct link is better than the relay link. As a result, we consider the direct link in our analysis and exploit the benefit provided by the relay channel in terms of diversity. Moreover, in practice, channel estimation is required to obtain the CSI, where the estimation errors are inevitable due to various factors such as the limited length of the training sequences and the time-varying nature of wireless channels. The performance degradation due to such estimation errors can be mitigated by using robust designs that take into account the possible estimation errors. As a result, robust methods are highly desired for practical applications. The robust techniques can be divided mainly into worst-case and stochastic approaches [16]. The worst-case approach [17, 18] considers that the errors belong to a predefined uncertainty region, where the objective is to optimize the worst system performance for any error in this region. The stochastic approach guarantees a certain system performance averaged over channel realizations [19]. The latter approach has been used in [20] to minimize the power of the transmit beamformer while satisfying the QoS requirements for all users. In the sequel, we use stochastic approach for the robust design.
In this paper, we deal with the joint robust design of source precoder, relay transceiver, and destination equalizer for an AF MIMO relay system where the CSI is considered to be imperfect at all nodes. A stochastic approach is employed in which the objective is to minimize the average sum mean-square error (If the channel estimation is perfect at the receiver, the minimum mean-square error (MMSE) matrix  can be related to the rate using the relation
can be related to the rate using the relation  . However, if the receiver does not have perfect estimation of the channel, the relation between the rate and MMSE matrix is not straightforward. Consequently, for our current system model where both the estimates of source-relay and relay-destination channels are imperfect, deriving rate expression and solving the optimization problem based on that expression are still an open issue.) under the source and relay power constraints. The considered joint optimization is nonconvex and also does not lead to closed-form solutions. However, it has been shown that the optimization of one parameter when others are fixed is a quadratic convex-optimization problem that can be easily solved within the framework of convex optimization techniques. We first propose an iterative approach both for the MIMO relay channels with and without the direct link. Although the iterative method guarantees fast convergence for the case with the direct link, the global optimality cannot be proven since the joint optimization problem is nonconvex. As a result, in the second part of this paper, we limit the joint optimization problem for the case without the direct link in which the source-relay and relay-destination MIMO channels have only transmit-side antenna correlations. In the latter case, it is shown that structures of the optimal source precoder and relay transceiver have closed forms, where the remaining joint power allocation problem can be approximately formulated into a Geometric Programming (GP) problem. With the help of computer simulations, we compare the solutions of the iterative technique and the GP approach under high signal-to-noise ratio (SNR) approximation for the case without the direct link. This comparison is helpful to conclude that the iterative approach gives reasonably good solutions with an acceptable complexity.
. However, if the receiver does not have perfect estimation of the channel, the relation between the rate and MMSE matrix is not straightforward. Consequently, for our current system model where both the estimates of source-relay and relay-destination channels are imperfect, deriving rate expression and solving the optimization problem based on that expression are still an open issue.) under the source and relay power constraints. The considered joint optimization is nonconvex and also does not lead to closed-form solutions. However, it has been shown that the optimization of one parameter when others are fixed is a quadratic convex-optimization problem that can be easily solved within the framework of convex optimization techniques. We first propose an iterative approach both for the MIMO relay channels with and without the direct link. Although the iterative method guarantees fast convergence for the case with the direct link, the global optimality cannot be proven since the joint optimization problem is nonconvex. As a result, in the second part of this paper, we limit the joint optimization problem for the case without the direct link in which the source-relay and relay-destination MIMO channels have only transmit-side antenna correlations. In the latter case, it is shown that structures of the optimal source precoder and relay transceiver have closed forms, where the remaining joint power allocation problem can be approximately formulated into a Geometric Programming (GP) problem. With the help of computer simulations, we compare the solutions of the iterative technique and the GP approach under high signal-to-noise ratio (SNR) approximation for the case without the direct link. This comparison is helpful to conclude that the iterative approach gives reasonably good solutions with an acceptable complexity.
The remainder of this paper is organized as follows. The system model for MIMO relay channel is presented in Section 2. In Section 3, the iterative approach is described for jointly optimizing the source precoder, relay transceiver, and destination equalizer for the MIMO relay channel with the direct link. The closed-form solutions and the approximate GP problem formulation are provided in Section 4 for the MIMO relay channel without the direct link where single-side antenna correlations have been considered for source-relay and relay-destination channels. In Section 5, simulation results are presented to show the performance of the proposed robust and nonrobust methods, and in Section 6, conclusions are drawn.
Notations
Upper (lower) bold face letters will be used for matrices (vectors);  ,
,  ,
,  ,
,  ,
,  , and
, and  denote conjugate, transpose, Hermitian transpose, mathematical expectation,
denote conjugate, transpose, Hermitian transpose, mathematical expectation,  identity matrix, and Frobenius norm, respectively.
identity matrix, and Frobenius norm, respectively.  ,
,  ,
,  ,
,  denote the matrix trace operator, vectorization operator, space of
denote the matrix trace operator, vectorization operator, space of  matrices with complex entries, and the Kronecker product, respectively.
matrices with complex entries, and the Kronecker product, respectively.
2. System Model
We consider a cooperative communication system that consists of a source, a relay, and a destination which are all multiantenna nodes. The block diagram is shown in Figure 1. Notice that the direct link between the source and destination is taken into account, so that the diversity order of the cooperative system can be maintained. The source has  antennas, the relay has
antennas, the relay has  receiving antennas and
receiving antennas and  transmitting antennas, and the destination has
transmitting antennas, and the destination has  antennas. The relay protocol consists of two timeslots. In the first timeslot, the source sends a symbol vector to the destination and relay. The relay linearly processes the source symbol vector and sends it to the destination in the second timeslot. The source remains idle during the second timeslot. At the end of two time slots, the destination linearly combines the symbol vectors received from the source and relay [1]. It is assumed that the estimates of the source-relay, relay-destination, and source-destination channels are available instead of their exact knowledge. The MIMO channels are considered to be spatially correlated block-fading frequency-flat Rayleigh channels. The signal received by the relay is given by
antennas. The relay protocol consists of two timeslots. In the first timeslot, the source sends a symbol vector to the destination and relay. The relay linearly processes the source symbol vector and sends it to the destination in the second timeslot. The source remains idle during the second timeslot. At the end of two time slots, the destination linearly combines the symbol vectors received from the source and relay [1]. It is assumed that the estimates of the source-relay, relay-destination, and source-destination channels are available instead of their exact knowledge. The MIMO channels are considered to be spatially correlated block-fading frequency-flat Rayleigh channels. The signal received by the relay is given by

where  is the complex source signal of length
is the complex source signal of length  ,
,  is the precoder that maps the
is the precoder that maps the  symbol vector into
symbol vector into  source antennas,
source antennas,  is the MIMO channel between the source and relay, and
is the MIMO channel between the source and relay, and  is the additive Gaussian noise vector at the relay. We also assume that the elements of
is the additive Gaussian noise vector at the relay. We also assume that the elements of  are statistically independent with the zero-mean and unit variance, that is,
are statistically independent with the zero-mean and unit variance, that is,  . The precoder
. The precoder  at the source operates under the power constraint
at the source operates under the power constraint  , where
, where  is the maximum power of the source. We consider
is the maximum power of the source. We consider  , that is, the entries of
, that is, the entries of  are zero-mean circularly symmetric complex Gaussian (ZMCSCG) with the variance
are zero-mean circularly symmetric complex Gaussian (ZMCSCG) with the variance  . In order to ensure that the symbol
. In order to ensure that the symbol  can be recovered at the destination, it is assumed that
can be recovered at the destination, it is assumed that  ,
,  , and
, and  are greater than or equal to
are greater than or equal to  . The signal received by the destination in first timeslot can be expressed as follows:
. The signal received by the destination in first timeslot can be expressed as follows:

where  is the MIMO channel between the source and destination and
is the MIMO channel between the source and destination and  is the additive Gaussian noise vector at the destination and follows
is the additive Gaussian noise vector at the destination and follows  . The MIMO relay processes the signal
. The MIMO relay processes the signal  using the linear operator
using the linear operator  and forwards the following signal to the destination in the second timeslot:
and forwards the following signal to the destination in the second timeslot:

where the relay transceiver  operates under the power constraint
operates under the power constraint  with total relay power of
with total relay power of  . The signal received by the destination in the second timeslot is
. The signal received by the destination in the second timeslot is

where  is the MIMO channel between the relay and destination and
is the MIMO channel between the relay and destination and  is the additive noise described as
is the additive noise described as  . The double-sided spatially correlated source-relay, relay-destination and source-destination are modelled according to Kronecker model as follows:
. The double-sided spatially correlated source-relay, relay-destination and source-destination are modelled according to Kronecker model as follows:

where  ,
,  , and
, and  are the receive-side spatial correlation matrices, and
are the receive-side spatial correlation matrices, and  ,
,  , and
, and  are the transmit-side correlation matrices for the channels
are the transmit-side correlation matrices for the channels  ,
,  , and
, and  , respectively. The elements of
, respectively. The elements of  ,
,  , and
, and  are ZMCSCG random variables with the unit variance. Note that the transmit and receive spatial correlation matrices are positive semidefinite matrices and are a function of the antenna spacing, average direction of arrival/departure of the wavefronts at/from the transmitter/receiver, and the corresponding angular spread (see [21] and the references therein). The spatial correlation matrices represent the second-order statistics of the channels which vary slowly and can be precisely estimated. However, estimation of the fast fading parts
are ZMCSCG random variables with the unit variance. Note that the transmit and receive spatial correlation matrices are positive semidefinite matrices and are a function of the antenna spacing, average direction of arrival/departure of the wavefronts at/from the transmitter/receiver, and the corresponding angular spread (see [21] and the references therein). The spatial correlation matrices represent the second-order statistics of the channels which vary slowly and can be precisely estimated. However, estimation of the fast fading parts  ,
,  , and
, and  of the spatially correlated MIMO channels can lead to a significant amount of estimation error. For the linear minimum mean-square error (MMSE) estimation, we can write the following error model [22]:
of the spatially correlated MIMO channels can lead to a significant amount of estimation error. For the linear minimum mean-square error (MMSE) estimation, we can write the following error model [22]:

where  ,
,  , and
, and  are the estimated CSI, and
are the estimated CSI, and  ,
,  , and
, and  are the corresponding channel estimation errors whose elements are ZMCCSG random variables with the variances
are the corresponding channel estimation errors whose elements are ZMCCSG random variables with the variances  ,
,  , and
, and  , respectively. Substituting (6) into (5), the error modelling for the actual channels
, respectively. Substituting (6) into (5), the error modelling for the actual channels  ,
,  , and
, and  can be simply given by
can be simply given by

which shows that the errors  ,
,  , and
, and  are also double-sided correlated like the MIMO channels. The destination recovers the source signal
are also double-sided correlated like the MIMO channels. The destination recovers the source signal  by linearly combining the signals
by linearly combining the signals  (2) and
(2) and  (4) of two time slots as follows:
(4) of two time slots as follows:

where  denote the linear operators for the signals received from the direct and relay links, respectively. The MSE between
denote the linear operators for the signals received from the direct and relay links, respectively. The MSE between  and
and  can be defined as follows:
can be defined as follows:

where the MSE matrix depends on  ,
,  ,
,  and
and  and the mathematical expectation is only taken with respect to noise and signal realizations. Considering that
and the mathematical expectation is only taken with respect to noise and signal realizations. Considering that  ,
,  ,
,  and
and  are statistically independent and applying (2) and (4) into (8), we can write (9) as follows:
are statistically independent and applying (2) and (4) into (8), we can write (9) as follows:

For the given channel estimates  ,
,  , and
, and  , the MSE matrix of (10) is random due to the random errors
, the MSE matrix of (10) is random due to the random errors  ,
,  , and
, and  . Since the exact errors are not known and only the covariance matrices of these errors are known, we need to derive the average MSE matrix. This can be done by averaging the MSE matrix (10) over the independent errors
. Since the exact errors are not known and only the covariance matrices of these errors are known, we need to derive the average MSE matrix. This can be done by averaging the MSE matrix (10) over the independent errors  ,
,  , and
, and  . Hence, we can write
. Hence, we can write

where  , and we have applied (7) and used the facts that
, and we have applied (7) and used the facts that  is zero-mean and
is zero-mean and  for
for  . Similarly, since
. Similarly, since  ,
,  , and
, and  are independent, we can easily show that
are independent, we can easily show that

Furthermore, we can write

where the inner expectation is

and  . Substituting the result of (14) into (13), we have
. Substituting the result of (14) into (13), we have

where  . Applying similar steps, we can also get
. Applying similar steps, we can also get

Using the results of (11) to (16), the average MSE matrix can be written as follows:

where  . The instantaneous relay power can be obtained as follows:
. The instantaneous relay power can be obtained as follows:

where expectation is taken w.r.t. noise and signal realizations. After including the estimation error  in (18), the relay power averaged over
in (18), the relay power averaged over  can be expressed with the help of (14) as follows:
can be expressed with the help of (14) as follows:

3. Joint Optimization: Iterative Approach
The objective of joint optimization is to minimize the sum of the average MSE (17) under power constraints of the source and relay. This optimization problem can be expressed as follows:

The constraints of the optimization problem (20) do not depend on  and
and  . As a result, the optimal
. As a result, the optimal  and
and  can be easily obtained in terms of
can be easily obtained in terms of  and
and  . Unfortunately, after substituting such optimal
. Unfortunately, after substituting such optimal  and
and  into the objective function of (20), the resulting objective function in terms of
into the objective function of (20), the resulting objective function in terms of  and
and  appears to be a nontractable nonconvex problem. This fact will be later shown in this section. The joint optimization problem (20) is a nonconvex problem and does not offer closed-form solutions. However, it can be easily observed that the considered problem is a convex problem over one optimization variable when others are fixed. Hence, we propose to solve this optimization problem using iterative technique, where each optimization variable is updated at a time considering others as fixed. The iterative algorithm may be implemented as follows. The destination estimates the source-destination and relay-destination channels and the relay estimates the source-relay channel, separately with the help of training sequence. The relay sends the estimated source-relay channel to the destination where the iterative algorithm is executed. The destination feedbacks optimally designed
appears to be a nontractable nonconvex problem. This fact will be later shown in this section. The joint optimization problem (20) is a nonconvex problem and does not offer closed-form solutions. However, it can be easily observed that the considered problem is a convex problem over one optimization variable when others are fixed. Hence, we propose to solve this optimization problem using iterative technique, where each optimization variable is updated at a time considering others as fixed. The iterative algorithm may be implemented as follows. The destination estimates the source-destination and relay-destination channels and the relay estimates the source-relay channel, separately with the help of training sequence. The relay sends the estimated source-relay channel to the destination where the iterative algorithm is executed. The destination feedbacks optimally designed  and
and  to the source and relay, respectively. The channel is considered to remain constant within a block but vary from one block to another, where the block consists of training signal and useful data (Notice that the adaptation of the source precoder and relay transceiver matrices in fast fading scenario can be impractical if the design is based on instantaneous channels [23]. Therefore, robust designs based on channel covariance information [20] can be appropriate for such a scenario. ).
to the source and relay, respectively. The channel is considered to remain constant within a block but vary from one block to another, where the block consists of training signal and useful data (Notice that the adaptation of the source precoder and relay transceiver matrices in fast fading scenario can be impractical if the design is based on instantaneous channels [23]. Therefore, robust designs based on channel covariance information [20] can be appropriate for such a scenario. ).
Remark 1.
It is worthwhile to mention here that the minimization of the sum of the source and relay powers under the MSE constraint can also be solved by using the iterative framework that we are proposing in the sequel. Moreover, the quality of fairness approach such as minimizing the sum of the source and relay powers while fulfilling the SNR/MSE requirements of each symbol stream can also be handled by the proposed iterative method. For conciseness, the latter two methods are not considered in this paper.
After solving the first-order partial derivative of the objective function of (20) w.r.t to  , we get
, we get

Substituting (21) into the objective of (20), the latter can be expressed in terms of  ,
,  , and
, and  as follows:
as follows:

Now, solving the derivative of (22) w.r.t to  , we get the optimal
, we get the optimal  as follows:
as follows:

The optimal  can be obtained by substituting
can be obtained by substituting  from (23) into (21). Using the results of (21) and (23) and then resubstituting
from (23) into (21). Using the results of (21) and (23) and then resubstituting  ,
,  , and
, and  , (22) can be written in terms of
, (22) can be written in terms of  and
and  as follows:
as follows:

where

It is interesting to observe that  is the MMSE matrix of the direct link, where the sum MMSE is simply given by
is the MMSE matrix of the direct link, where the sum MMSE is simply given by  . The second equality for
. The second equality for  in (25) is obtained by using the fact that
in (25) is obtained by using the fact that  . Applying the same fact and after some manipulations, we get
. Applying the same fact and after some manipulations, we get

where second equality is obtained after simple steps using the fact that  is a positive definite square matrix. Notice that
is a positive definite square matrix. Notice that  is only related to the MMSE of the double-hop channel, where the sum MMSE is
is only related to the MMSE of the double-hop channel, where the sum MMSE is  . With these observations, we can formulate the following lemma:
. With these observations, we can formulate the following lemma:
Lemma 1.
The sum MMSE of the MIMO relay system with the direct link is upper bounded by the sum MMSE of the direct link and source-relay-destination link.
Proof.
This Lemma can be easily proven by using the properties of the positive (semi) definite matrices. Since  is positive definite and
is positive definite and  and
and  are positive semidefinite, we can show that
are positive semidefinite, we can show that


The results of (27) and (28) prove the Lemma.
It can be seen that the minimization of (26) under source and relay power constraints is a nontractable problem. We have noticed that even in the case of the nonrobust design, such an objective is difficult to handle. This difficulty has motivated us to use the iterative optimization based on the MSE function (17) for which  and
and  have been already determined in terms of
have been already determined in terms of  and
and  (see (21) and (23)). In the following, we show the optimizations over
(see (21) and (23)). In the following, we show the optimizations over  and
and  when other variables are fixed.
when other variables are fixed.
(1) Optimization over 
With some straightforward manipulations of (17) and using the fact that  , the average sum MSE (objective function of (20)) can be alternatively expressed as follows:
, the average sum MSE (objective function of (20)) can be alternatively expressed as follows:

where  . Applying the following results [24]:
. Applying the following results [24]:

and denoting  , we can write
, we can write

where

The optimization problem w.r.t.  can be thus written as follows:
can be thus written as follows:

Noting that  , the optimization problem (33) can be written as follows:
, the optimization problem (33) can be written as follows:

Using the notation  , the fact that
, the fact that  and introducing an auxiliary variable
and introducing an auxiliary variable  , the problem (34) can be formulated as the following standard convex optimization problem:
, the problem (34) can be formulated as the following standard convex optimization problem:

where  ,
,  , and the quadratic inequality constraint
, and the quadratic inequality constraint  is converted to a linear matrix inequality constraint (LMI) using Schur-Complement theorem [16].
is converted to a linear matrix inequality constraint (LMI) using Schur-Complement theorem [16].
Remark 2.
Notice that when other variables are fixed,  can be optimized by solving the Karush-Kuhn-Tucker (KKT) conditions, where the Lagrangian multiplier that arises due to the relay power constraint can be obtained by using the bisection algorithm like in [15]. However, in order to make the proposed iterative approach applicable for other related problems briefly discussed in the beginning of this section and also for the optimization over
can be optimized by solving the Karush-Kuhn-Tucker (KKT) conditions, where the Lagrangian multiplier that arises due to the relay power constraint can be obtained by using the bisection algorithm like in [15]. However, in order to make the proposed iterative approach applicable for other related problems briefly discussed in the beginning of this section and also for the optimization over  in the sequel, we propose to formulate our optimization problem in the convex form
in the sequel, we propose to formulate our optimization problem in the convex form  , which has been proven to be computationally efficient and flexible to accommodate even a large number of convex constraints [16].
, which has been proven to be computationally efficient and flexible to accommodate even a large number of convex constraints [16].
(2) Optimization over 
First, we define the following scalars that do not depend on  :
:

After some simple steps and again using the fact that  in (17), the average sum MSE (20) can also be expressed as follows:
in (17), the average sum MSE (20) can also be expressed as follows:

where  and
and  . Noting that
. Noting that  [24] and applying (30), we can write
[24] and applying (30), we can write

where  . The relay power in terms of
. The relay power in terms of  can be expressed as follows:
can be expressed as follows:

where we have used  , and
, and  . The optimization problem w.r.t.
. The optimization problem w.r.t.  can be now formulated as follows:
can be now formulated as follows:

Finally, like in the case of the optimization over  , we can transform (40) into the following convex problem:
, we can transform (40) into the following convex problem:

where  and the LMI is equivalent to the quadratic inequality constraint like in the case of
and the LMI is equivalent to the quadratic inequality constraint like in the case of  . Note that the optimization problems
. Note that the optimization problems  and
and  can also be solved first by reformulating them as quadratic matrix programming [25] problems and then applying the semidefinite programming (SDP) relaxation technique. However, since our problems are already convex and second-order cone programming (SOCP) formulation is possible, applying SDP relaxation only increases the computational complexity as we know that the SDP has higher computational burden than the SOCP [26]. The iterative optimization technique can be now summarized as follows:
can also be solved first by reformulating them as quadratic matrix programming [25] problems and then applying the semidefinite programming (SDP) relaxation technique. However, since our problems are already convex and second-order cone programming (SOCP) formulation is possible, applying SDP relaxation only increases the computational complexity as we know that the SDP has higher computational burden than the SOCP [26]. The iterative optimization technique can be now summarized as follows:
Algorithm 1.
The iterative algorithm for joint optimization of  ,
,  ,
,  and
and  .
.
-
(1)
Initialize the algorithm with
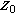 and
and 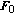 such that the source and relay power constraints are satisfied.
such that the source and relay power constraints are satisfied.-
(a)
repeat
-
(b)
Update
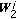 using (23).
using (23). -
(c)
Update
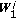 using (21) and (23).
using (21) and (23). -
(d)
Update
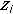 by solving the convex problem
by solving the convex problem 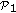 .
. -
(e)
Update
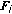 by solving the convex problem
by solving the convex problem 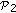 .
. -
(f)
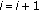 ;
;
-
(a)
-
(2)
until both
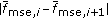 is smaller than a threshold
is smaller than a threshold  , where the index
, where the index  denotes the
denotes the  th iteration.
th iteration.
Remark 3.
In the case of the relay channel without the direct link, the optimization problem over destination equalizer,  and
and  can be iteratively solved by omitting all terms containing
can be iteratively solved by omitting all terms containing  and
and  in (23),
in (23),  , and
, and  .
.
Remark 4.
If the channel estimates are perfect, (21), (23),  , and
, and  can be changed to shorter forms by using the fact that
can be changed to shorter forms by using the fact that  . The resulting equations and optimization problems correspond to the perfect CSI case.
. The resulting equations and optimization problems correspond to the perfect CSI case.
3.1. Computational Complexity
The computational complexity of Algorithm 1 mainly depends on the work loads of the convex optimization problems  and
and  which consist of second-order cone (SOC) as well as SDP constraints. An enormous amount of effort will be required to compute the exact computational complexity of
which consist of second-order cone (SOC) as well as SDP constraints. An enormous amount of effort will be required to compute the exact computational complexity of  and
and  , and thus their exact complexity analysis is beyond the scope of this paper. However, using the results of [26], we determine the worst-case computational complexity of
, and thus their exact complexity analysis is beyond the scope of this paper. However, using the results of [26], we determine the worst-case computational complexity of  and
and  . In
. In  , there are
, there are  SOC constraints where the first SOC constraint has a dimension (also the size of the cone) with
SOC constraints where the first SOC constraint has a dimension (also the size of the cone) with  real variables and the remaining two SOC constraints have the same size of
real variables and the remaining two SOC constraints have the same size of  . The SOC constraints in
. The SOC constraints in  consist of
consist of  real optimization variables. The only one SDP constraint of
real optimization variables. The only one SDP constraint of  has a size of
has a size of  with
with  real optimization variables. Therefore, according to [26], the computational load of
real optimization variables. Therefore, according to [26], the computational load of  per iteration is
per iteration is  . The number of iterations required can be upper bounded by
. The number of iterations required can be upper bounded by  . Hence, the overall worst-case complexity of
. Hence, the overall worst-case complexity of  is
is  . Similarly, we can compute the worst-case computational load for
. Similarly, we can compute the worst-case computational load for  . The first SOC constraint in
. The first SOC constraint in  has a size of
has a size of  while the other SOC constraints are of the same size of
while the other SOC constraints are of the same size of  . The SOC constraints consist of
. The SOC constraints consist of  real optimization variables. Like in the case of
real optimization variables. Like in the case of  , the single SDP constraint is of size
, the single SDP constraint is of size  with
with  real optimization variables. Thus (see also [26]), we find that
real optimization variables. Thus (see also [26]), we find that  has a work load of
has a work load of  per iteration, where the required number of iterations is upper bounded by
per iteration, where the required number of iterations is upper bounded by  . As a result, the worst-case complexity of
. As a result, the worst-case complexity of  is
is  . Notice that in practice the interior-point algorithms used for solving
. Notice that in practice the interior-point algorithms used for solving  and
and  behave much better than predicted by the aforementioned worst-case analysis [27].
behave much better than predicted by the aforementioned worst-case analysis [27].
3.2. Convergence Analysis
It can be shown that the proposed iterative method converges. It has been already discussed that the optimization problem is convex w.r.t. each variable when the others are fixed. For the given  and
and  , the solutions given by (21) and (23) correspond to the MMSE receiver. As a result, we have
, the solutions given by (21) and (23) correspond to the MMSE receiver. As a result, we have  . Similarly, for the given
. Similarly, for the given  ,
,  , and
, and  , the optimization problem (20) is convex w.r.t.
, the optimization problem (20) is convex w.r.t.  and, thus, the problem
and, thus, the problem  provides optimal solution for
provides optimal solution for  which means that
which means that  . Finally, for the given
. Finally, for the given  ,
,  , and
, and  , problem (20) is convex w.r.t.
, problem (20) is convex w.r.t.  and, hence, the problem
and, hence, the problem  gives optimal solution for
gives optimal solution for  thereby confirming
thereby confirming  . Therefore, it can be found that with each update of
. Therefore, it can be found that with each update of  ,
,  ,
,  , and
, and  , the objective function decreases and the iterative method converges. It will be later shown via numerical results that the iterative algorithm gives satisfactory performance with acceptable convergence speed. However, the global optimality of the solutions of the iterative method for the relay channel with the direct link cannot be guaranteed as the joint problem is nonconvex. In the next section, the joint optimization problem will be restricted to a double-hop MIMO relay, where receive antenna correlations are assumed to be negligible for each hop. In this case, the optimization problem turns to the joint power allocation, for which the global optimality can be guaranteed under high-SNR approximation.
, the objective function decreases and the iterative method converges. It will be later shown via numerical results that the iterative algorithm gives satisfactory performance with acceptable convergence speed. However, the global optimality of the solutions of the iterative method for the relay channel with the direct link cannot be guaranteed as the joint problem is nonconvex. In the next section, the joint optimization problem will be restricted to a double-hop MIMO relay, where receive antenna correlations are assumed to be negligible for each hop. In this case, the optimization problem turns to the joint power allocation, for which the global optimality can be guaranteed under high-SNR approximation.
4. Joint Power Allocation with GP: Without Direct Link
Due to severe shadowing, hotspots, and so forth, the destination may be out of the coverage area of the source. In such a scenario, it is reasonable to consider that the direct link between the source and destination does not exist. In the latter case of the relay channel without the direct link, the sum MSE can be expressed in terms of  and
and  (see also (28)) as follows:
(see also (28)) as follows:

The objective is to minimize the average sum MSE (42) under the constraints of source and relay powers. Thus, the optimization problem is

where the MMSE matrix is  . Let
. Let  be the vector of eigenvalues and
be the vector of eigenvalues and  be the vector of the diagonal elements of
be the vector of the diagonal elements of  in decreasing order. In this case,
in decreasing order. In this case,  is said to be majorized by
is said to be majorized by  , and the Schur-concave function can be defined as
, and the Schur-concave function can be defined as  , where
, where  stands for the function of
stands for the function of  . It is clear that the minimum of this function is obtained if the diagonal elements of
. It is clear that the minimum of this function is obtained if the diagonal elements of  become its eigenvalues [8]. This can occur when
become its eigenvalues [8]. This can occur when  is a diagonal matrix with its elements in decreasing order. Let the singular value decompositions of
is a diagonal matrix with its elements in decreasing order. Let the singular value decompositions of  and
and  be
be

where the diagonal elements of  and
and  are considered to be in the decreasing order. If these elements are not in decreasing order, some permutation matrices can be applied to make the diagonal elements of
are considered to be in the decreasing order. If these elements are not in decreasing order, some permutation matrices can be applied to make the diagonal elements of  and
and  in the decreasing order [8]. This means that, in (44), the permutation matrices are implicitly included. The closed-form expressions for the optimal
in the decreasing order [8]. This means that, in (44), the permutation matrices are implicitly included. The closed-form expressions for the optimal  and
and  are difficult to obtain in general. However, for the double-hop channels without receive-side antenna correlations, that is, when
are difficult to obtain in general. However, for the double-hop channels without receive-side antenna correlations, that is, when  and
and  , the optimal
, the optimal  and
and  that diagonalize the MMSE matrix can be given by
that diagonalize the MMSE matrix can be given by

where  and
and  are the diagonal matrices with the elements in decreasing order. Substituting (44) and (45) into the MMSE matrix and after some straightforward steps, we get
are the diagonal matrices with the elements in decreasing order. Substituting (44) and (45) into the MMSE matrix and after some straightforward steps, we get

where

In (47), we use  and
and  . Similarly, the source and relay powers become
. Similarly, the source and relay powers become

Let  and
and  , and
, and  and let
and let  be the nonzero diagonal elements of
be the nonzero diagonal elements of  and
and  , respectively, in the decreasing order. For brevity, we also define
, respectively, in the decreasing order. For brevity, we also define

where  and
and  are the
are the  th diagonal elements of
th diagonal elements of  and
and  , respectively, and
, respectively, and  . Since
. Since  and
and  are positive semidefinite, we have
are positive semidefinite, we have  and
and  for all
for all  . Using (47) and (49), the sum MMSE can be finally expressed as follows:
. Using (47) and (49), the sum MMSE can be finally expressed as follows:

where  is the SNR of each data stream provided that
is the SNR of each data stream provided that  is also smaller than or equal to
is also smaller than or equal to  and
and  . It is interesting to note that when the channel estimates are perfect, that is, when
. It is interesting to note that when the channel estimates are perfect, that is, when  , the sum MMSE of (50) reduces to the objective function of [28]. Applying (48), the joint power allocation problem can be formulated as follows:
, the sum MMSE of (50) reduces to the objective function of [28]. Applying (48), the joint power allocation problem can be formulated as follows:

which is a nonlinear and nonconvex problem. Since this problem is nonconvex, the global optimal solution is difficult to obtain. Considering the fact that the global optimal solutions of the problems similar to the nonrobust version of (51) can be obtained only with very high computational cost (see [29, 30]), the authors of [31] use an iterative waterfilling technique to solve the nonrobust form of (51). However, we have noticed that it is hard to solve (51) using the waterfilling method of [31]. The major difficulty arises from the fact that the first-order partial derivatives of the corresponding Lagrangian function w.r.t.  for the fixed
for the fixed  and w.r.t.
and w.r.t.  for the given
for the given  do not lead to equations that are decoupled in
do not lead to equations that are decoupled in  and
and  , respectively. It is easier to see that this difficulty appears due to the reason that
, respectively. It is easier to see that this difficulty appears due to the reason that  ,
,  , and
, and  in (51) consist of not only
in (51) consist of not only  and
and  but also
but also  and
and  , for all
, for all . Furthermore, although iterative waterfilling method is computationally efficient, it does not guarantee the global optimal solution. In the following, we use an alternative approach based on GP technique. Note that the optimization problem (51) is not a GP problem but a signomial programming (SP) problem [16] which can be iteratively solved as a GP problem after approximating the required posynomial terms by monomial terms. It is known that the SPs do not guarantee global optimality and the computational cost is high. Thus, using the high-SNR approximation, (51) can be solved as a GP whose global optimality can be confirmed. In this regard, we have
. Furthermore, although iterative waterfilling method is computationally efficient, it does not guarantee the global optimal solution. In the following, we use an alternative approach based on GP technique. Note that the optimization problem (51) is not a GP problem but a signomial programming (SP) problem [16] which can be iteratively solved as a GP problem after approximating the required posynomial terms by monomial terms. It is known that the SPs do not guarantee global optimality and the computational cost is high. Thus, using the high-SNR approximation, (51) can be solved as a GP whose global optimality can be confirmed. In this regard, we have

Using the upper bound (52), the power optimization problem can be expressed as follows:

which is a GP problem that can be solved efficiently to guarantee the global optimality.
Remark 5.
Notice that the joint power allocation problem is nonconvex even for the case without channel estimation errors [32]. In such a nonrobust design, it has been shown in [28] that the lower and upper bounds can be established for the MSE for each data stream. Unfortunately, this is not the case for the proposed robust design due to the fact that the terms  ,
,  , and
, and  are again functions of
are again functions of  for all
for all  and
and  for all
for all  . It is also worthwhile to note that several optimization problems which can be solved using the GP method and still provide solutions close to the optimal solution of the sum MSE minimization problem are; (a) maximization of the minimum of the SNRs of the data streams and (b) maximization of the geometric mean of the SNRs of the data streams, both under the source and relay power constraints.
. It is also worthwhile to note that several optimization problems which can be solved using the GP method and still provide solutions close to the optimal solution of the sum MSE minimization problem are; (a) maximization of the minimum of the SNRs of the data streams and (b) maximization of the geometric mean of the SNRs of the data streams, both under the source and relay power constraints.
5. Numerical Results and Discussions
In this section, the performance of the proposed methods will be investigated. The proposed robust designs are also compared with the nonrobust case, where the channel estimation errors are not taken into account. Notice that the nonrobust design corresponds to the so called naïve design, where the optimization problems of interest are solved assuming that there are no errors in channel estimates (see also Remark 4) although in reality the estimates are erroneous. For all numerical simulations, we take  ,
,  ,
,  ,
,  , and
, and  . The spatial covariance matrices for source-relay, relay-destination, and source-destination channels are modelled according to the widely used exponential correlation model. In our examples, we take
. The spatial covariance matrices for source-relay, relay-destination, and source-destination channels are modelled according to the widely used exponential correlation model. In our examples, we take

In all cases, the optimization problems  ,
,  , and (53) are solved using the CVX software [33]. The SNRs for source-relay, source-destination, and relay-destination channels are defined as
, and (53) are solved using the CVX software [33]. The SNRs for source-relay, source-destination, and relay-destination channels are defined as  ,
,  , and
, and  , respectively. Throughout all examples, we take
, respectively. Throughout all examples, we take  dBw and vary the values of
dBw and vary the values of  and
and  to change
to change  ,
,  , and
, and  . The estimated channels are generated according to (7), so that the elements of actual channels
. The estimated channels are generated according to (7), so that the elements of actual channels  ,
,  , and
, and  have the variance of 1. For all results, we compute the average MSE by taking 200 realizations of the estimated channels.
have the variance of 1. For all results, we compute the average MSE by taking 200 realizations of the estimated channels.
The convergence behaviour of the proposed iterative method as a function of iteration index is illustrated in Figure 2 for the relay channel with the direct link. The parameters in this figure are set as  ,
,  ,
,  , and
, and  . We take three sets of SNRs as
. We take three sets of SNRs as  dB,
dB,  dB and
dB and  dB, and
dB, and  dB. It can be seen from this figure that the iterative method converges in about 15 iterations. The convergence is faster for the lower values of the SNR. The effect of different initializations on the convergence behaviours of the iterative method is also displayed in Figure 2. The convergence speed for the cases where
dB. It can be seen from this figure that the iterative method converges in about 15 iterations. The convergence is faster for the lower values of the SNR. The effect of different initializations on the convergence behaviours of the iterative method is also displayed in Figure 2. The convergence speed for the cases where  and
and  are initialized to randomly generated matrices of ZMCSCG random variables is similar to the cases where
are initialized to randomly generated matrices of ZMCSCG random variables is similar to the cases where  and
and  are initialized to the matrices proportional to identity (i.e.,
are initialized to the matrices proportional to identity (i.e.,  and
and  ). Moreover, it can be noticed from Figure 2 that different initializations lead to the similar solutions. In Figure 3, the performance of the iterative method as a function of the iteration index is illustrated for the relay channel without the direct link. We take
). Moreover, it can be noticed from Figure 2 that different initializations lead to the similar solutions. In Figure 3, the performance of the iterative method as a function of the iteration index is illustrated for the relay channel without the direct link. We take  ,
,  , and
, and  in this figure. As a reference, the performance of the GP problem which gives optimal solution under high-SNR assumption is also displayed in Figure 3. It can be noticed from Figure 3 that the difference between the solutions of the iterative method and GP method is negligible after 10–15 iterations.
in this figure. As a reference, the performance of the GP problem which gives optimal solution under high-SNR assumption is also displayed in Figure 3. It can be noticed from Figure 3 that the difference between the solutions of the iterative method and GP method is negligible after 10–15 iterations.
The performance of the proposed iterative method for the MIMO relay channel with the direct link is shown in Figure 4 for different values of  . The performance of the nonrobust method which considers the estimated channels as actual channels and the performance of the robust method without a source precoder [15] (the case with
. The performance of the nonrobust method which considers the estimated channels as actual channels and the performance of the robust method without a source precoder [15] (the case with  where
where  is the positive scaling factor chosen for satisfying the source power constraint) are also displayed in this figure. We keep
is the positive scaling factor chosen for satisfying the source power constraint) are also displayed in this figure. We keep  ,
,  , and
, and  dB and change
dB and change  and
and  from
from  to
to  dB. The threshold
dB. The threshold  for stopping the iterative process is set to
for stopping the iterative process is set to  . It can be noticed from this figure that in all cases, the MSE decreases when the SNR increases and when the variance of the channel estimation error
. It can be noticed from this figure that in all cases, the MSE decreases when the SNR increases and when the variance of the channel estimation error  decreases. Furthermore, the proposed robust design outperforms both the nonrobust method and the robust method with
decreases. Furthermore, the proposed robust design outperforms both the nonrobust method and the robust method with  [15]. In Figure 5, the performance between the proposed iterative method and the GP power allocation method for the relay channel without the direct link is compared. This figure displays the sum MSE as a function of the correlation coefficient
[15]. In Figure 5, the performance between the proposed iterative method and the GP power allocation method for the relay channel without the direct link is compared. This figure displays the sum MSE as a function of the correlation coefficient  for different values of
for different values of  and
and  . We keep
. We keep  ,
,  and
and  for Figure 5. It can be observed from this figure that the proposed robust methods significantly outperform the nonrobust method. Moreover, the performance gap between the iterative approach and the GP power allocation method is negligible for
for Figure 5. It can be observed from this figure that the proposed robust methods significantly outperform the nonrobust method. Moreover, the performance gap between the iterative approach and the GP power allocation method is negligible for  . For
. For  , the iterative approach outperforms the GP method. In all cases, the sum MSE increases with the increasing values of correlation coefficient.
, the iterative approach outperforms the GP method. In all cases, the sum MSE increases with the increasing values of correlation coefficient.
6. Conclusions
The problem of jointly optimizing the source precoder, relay transceiver, and destination equalizer for a cooperative MIMO relay system has been treated in this paper. An iterative approach with the guaranteed convergence has been proposed to solve the nonconvex problem. It has been shown that for the case without the direct link where the two-hop MIMO channels have only transmit-side antenna correlations, the joint optimization turns to the joint source and relay power allocation problem which has been solved by using GP technique under high-SNR approximation. Simulation results confirm the efficiency and good performance of the iterative approach for the MIMO relay channel with and without the direct link. Furthermore, the proposed robust methods significantly outperform the nonrobust method when the channel estimates are imperfect.
References
Laneman JN, Wornell GW: Exploiting distributed spatial diversity in wireless networks. Proceedings of the Allerton Conference on Communication, Control, and Computing, October 2000, Monticello, Ill, USA
Janani M, Hedayat A, Hunter TE, Nosratinia A: Coded cooperation in wireless communications: space-time transmission and iterative decoding. IEEE Transactions on Signal Processing 2004, 52(2):362-371. 10.1109/TSP.2003.821100
Kramer G, Gastpar M, Gupta P: Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory 2005, 51(9):3037-3063. 10.1109/TIT.2005.853304
Nabar RU, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004, 22(6):1099-1109. 10.1109/JSAC.2004.830922
Jing Y, Jafarkhani H: Using orthogonal and quasi-orthogonal designs in wireless relay networks. IEEE Transactions on Information Theory 2007, 53(11):4106-4118.
Havary-Nassab V, Shahbazpanahi S, Grami A, Luo Z-Q: Distributed beamforming for relay networks based on second-order statistics of the channel state information. IEEE Transactions on Signal Processing 2008, 56(9):4306-4316.
Wang B, Zhang J, Høst-Madsen A: On the capacity of MIMO relay channels. IEEE Transactions on Information Theory 2005, 51(1):29-43.
Muñoz-Medina O, Vidal J, Agustín A: Linear transceiver design in nonregenerative relays with channel state information. IEEE Transactions on Signal Processing 2007, 55: 2593-2604.
Tang X, Hua Y: Optimal design of non-regenerative MIMO wireless relays. IEEE Transactions on Wireless Communications 2007, 6(4):1398-1406.
Chae C-B, Tang T, Heath RW Jr., Cho S: MIMO relaying with linear processing for multiuser transmission in fixed relay networks. IEEE Transactions on Signal Processing 2008, 56(2):727-738.
Zhang R, Chai CC, Liang Y-C: Joint beamforming and power control for multiantenna relay broadcast channel with QoS constraints. IEEE Transactions on Signal Processing 2009, 57(2):726-737.
Chalise BK, Vandendorpe L: MIMO relay design for multipoint-to-multipoint communications with imperfect channel state information. IEEE Transactions on Signal Processing 2009, 57(7):2785-2796.
Behbahani AS, Merched R, Eltawil AM: Optimizations of a MIMO relay network. IEEE Transactions on Signal Processing 2008, 56(10):5062-5073.
Guan W, Luo H, Chen W: Linear relaying scheme for MIMO relay system with QoS requirements. IEEE Signal Processing Letters 2008, 15: 697-700.
Chengweng X, Shaodan M, Yik-Chung W: Robust joint design of linear precoder and destination equalizer for dual-hop amplifyand-forward MIMO relay systems. IEEE Transactions on Signal Processing 2010, 58(4):2273-2283.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Vorobyov SA, Gershman AB, Luo Z-Q: Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem. IEEE Transactions on Signal Processing 2003, 51(2):313-324. 10.1109/TSP.2002.806865
Pascual-Iserte A, Pérez Palomar D, Pérez-Neira AI, Lagunas MÁ: A robust maximin approach for MIMO communications with imperfect channel state information based on convex optimization. IEEE Transactions on Signal Processing 2006, 54(1):346-360.
Zhang X, Palomar DP, Ottersten B: Statistically robust design of linear MIMO transceivers. IEEE Transactions on Signal Processing 2008, 56: 3678-3689.
Chalise BK, Shahbazpanahi S, Czylwik A, Gershman AB: Robust downlink beamforming based on outage probability specifications. IEEE Transactions on Wireless Communications 2007, 6(10):3498-3503.
Luo J, Zeidler JR, McLaughlin S: Performance analysis of compact antenna arrays with MRC in correlated Nakagami fading channels. IEEE Transactions on Vehicular Technology 2001, 50(1):267-277. 10.1109/25.917940
Yoo T, Goldsmith A: Capacity of fading MIMO channels with channel estimation error. Proceedings of the IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 808-813.
Zhou S, Giannakis GB: Optimal transmitter eigen-beamforming and space-time block coding based on channel correlations. IEEE Transactions on Information Theory 2002, 49(7):1673-1690.
Horn RA, Johnson CR: Topics in Matrix Analysis. Cambridge University Press, Cambridge, UK; 1991.
Beck A: Quadratic matrix programming. SIAM Journal on Optimization 2007, 17(4):1224-1238. 10.1137/05064816X
Lobo MS, Vandenberghe L, Boyd S, Lebret H: Applications of second-order cone programming. Linear Algebra and Its Applications 1998, 284(1–3):193-228.
Eldar YC, Ben-Tal A, Nemirovski A: Robust mean-squared error estimation in the presence of model uncertainties. IEEE Transactions on Signal Processing 2005, 53(1):168-181.
Li C, Wang X, Yang L, Zhu W-P: A joint source and relay power allocation scheme for a class of MIMO relay systems. IEEE Transactions on Signal Processing 2009, 57(12):4852-4860.
Zhang W, Mitra U, Chiang M: Optimization of amplify-and-forward multicarrier two-hop transmission. submitted to IEEE Transactions on Communications
Cendrillon R, Yu W, Moonen M, Verlinden J, Bostoen T: Optimal multiuser spectrum balancing for digital subscriber lines. IEEE Transactions on Communications 2006, 54(5):922-933.
Rong Y, Tang X, Hua Y: A unified framework for optimizing linear nonregenerative multicarrier MIMO relay communication systems. IEEE Transactions on Signal Processing 2009, 57(12):4837-4851.
Hammerstrom I, Wittneben A: Power allocation for amplify and forward MIMO-OFDM relay links. IEEE Transactions on Wireless Communications 2007, 6(5):1774-1786.
Grant M, Boyd S: CVX: Matlab software for disciplined convex programming. June 2009, http://stanford.edu/~boyd/cvx
Acknowledgments
This work is supported by the European project NEWCOM++, the Wallone region project COSMOS, and the concerted action SCOOP. B. K. Chalise is currently with the Center for Advanced Communications, Villanova University, Villanova, PA 19085, USA, (Phone:  1-610-519-7371, Fax:
1-610-519-7371, Fax:  1-610-519-6118, Email: batu.chalise@villanova.edu). L. Vandendorpe is with the Communication and Remote Sensing Laboratory, Universitè catholique de Louvain, Place du Levant, 2, B-1348 Louvain la Neuve, Belgium, (Phone:
1-610-519-6118, Email: batu.chalise@villanova.edu). L. Vandendorpe is with the Communication and Remote Sensing Laboratory, Universitè catholique de Louvain, Place du Levant, 2, B-1348 Louvain la Neuve, Belgium, (Phone:  32-10-472312, Fax:
32-10-472312, Fax:  32-10-472089, Email: luc.vandendorpe@uclouvain.be). The first author completed his part of contribution when he was with the Communication and Remote Sensing Laboratory, Universitè Catholique de Louvain.
32-10-472089, Email: luc.vandendorpe@uclouvain.be). The first author completed his part of contribution when he was with the Communication and Remote Sensing Laboratory, Universitè Catholique de Louvain.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chalise, B.K., Vandendorpe, L. Joint Linear Processing for an Amplify-and-Forward MIMO Relay Channel with Imperfect Channel State Information. EURASIP J. Adv. Signal Process. 2010, 640186 (2010). https://doi.org/10.1155/2010/640186
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/640186

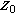 and
and 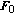 such that the source and relay power constraints are satisfied.
such that the source and relay power constraints are satisfied.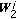 using (23).
using (23).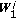 using (21) and (23).
using (21) and (23).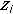 by solving the convex problem
by solving the convex problem 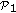 .
.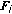 by solving the convex problem
by solving the convex problem 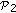 .
.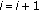 ;
;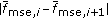 is smaller than a threshold
is smaller than a threshold  , where the index
, where the index  denotes the
denotes the  th iteration.
th iteration.
 ).
).
 ).
).
 ).
).
 ).
).