- Research Article
- Open access
- Published:
Noiseless Codelength in Wavelet Denoising
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 641842 (2010)
Abstract
We propose an adaptive, data-driven thresholding method based on a recently developed idea of Minimum Noiseless Description Length (MNDL). MNDL Subspace Selection (MNDL-SS) is a novel method of selecting an optimal subspace among the competing subspaces of the transformed noisy data. Here we extend the application of MNDL-SS for thresholding purposes. The approach searches for the optimum threshold for the data coefficients in an orthonormal basis. It is shown that the optimum threshold can be extracted from the noisy coefficients themselves. While the additive noise in the available data is assumed to be independent, the main challenge in MNDL thresholding is caused by the dependence of the additive noise in the sorted coefficients. The approach provides new hard and soft thresholds. Simulation results are presented for orthonormal wavelet transforms. While the method is comparable with the existing thresholding methods and in some cases outperforms them, the main advantage of the new approach is that it provides not only the optimum threshold but also an estimate of the associated mean-square error (MSE) for that threshold simultaneously.
1. Introduction
We can recognize different phenomena by collecting data from them. However, defective instruments, problems with the data acquisition process, and the interference of natural factors can all degrade the data of interest. Furthermore, noise can be introduced by transmission errors or compression. Thus, denoising is often a necessary step in data processing and various approaches have been introduced for this purpose. Some of these methods, such as Wiener filters, are grouped as linear techniques. While these techniques are easy to implement, their results are not always satisfactory. Over past decades, researchers have improved the performance of denoising methods by developing nonlinear approaches such as [1–6]. Although these approaches have succeeded in providing better results, they are usually computationally exhaustive, hard to implement, or use particular assumptions either on the noisy data or on the class of the data estimator.
Thresholding methods are alternative approaches to the denoising problem. The thresholding problem is first formulated in [7] where VisuShrink is introduced. This threshold is a nonadaptive universal threshold and depends only on the number of data points and noise variance. VisuShrink is a wavelet thresholding method which is both simple and effective in comparison with other denoising techniques. When an orthogonal wavelet basis is used, the coefficients with small absolute values tend to be attributed to the additive noise. Taking advantage of this property, finding a proper threshold, and setting all absolute values of coefficients smaller than the threshold to zero can suppress the noise. The main issue in such approaches is to find a proper threshold. In using the thresholding method for image denoising, the visual quality of the image is of great concern. An improper threshold may introduce artifacts and cause blurring of the image. One of the first soft thresholding methods is SureShrink [8] which has a better effect on the image than Visushrink in many cases. This method uses a hybrid of the universal threshold and the SURE (Stein's Unbiased Risk Estimator) threshold. The SURE threshold is chosen by minimizing Stein's estimate.
In this research we focus on the mean-square error (MSE) associated with the denoising process. The importance of this error in any signal reconstruction and estimation is inevitable [9, 10]. After all, in any estimation process, in this case reconstructing the denoised signal from the noisy one, the major goal is to achieve the original signal as much as possible, and the MSE is one of the most used criteria for evaluation purposes. To find the optimum threshold we estimate the MSE of a set of completing thresholds and choose the one that minimizes this error. The fundamentals of MSE estimation are similar to the method proposed in Minimum Noiseless Description Length (Codelength) Subspace Selection (MNDL-SS) [10]. Each subspace in this approach keeps a subset of the coefficients and discards the rest. Thresholding also produces a subspace that includes a set of coefficients that are being kept. On the other hand, it was shown in [10] that an estimate of noiseless description length (NDL) can be provided for each subspace by using the noisy data itself. We also show that in the process of estimating the NDL, the estimates of MSE is also provided. Furthermore comparison of the NDL of competing subspaces is equivalent to comparison of their MSEs. Therefore, the method presented in this paper is denoted by MNDL thresholding. The competing thresholds that are the sorted coefficients generate competing subspaces. For these subspaces the estimate of MSEs are provided and compared. The optimum threshold is associated with the subspace with minimum MSE (equivalently minimum NDL). Because of the particular choice of competing subspaces in MNDL thresholding, the effect of the additive noise is different from that in MNDL-SS. While the independence of the additive noise in MNDL-SS is the main advantage in estimating the desired NDL, in the case of thresholding, the additive noise is highly dependent. The main challenge in this work is to develop a method for NDL estimation acknowledging the presence of this noise dependence. We provide a threshold that is a function of the noise variance  , the data length
, the data length  , and the observed noisy data itself.
, and the observed noisy data itself.
The paper is arranged as follows. Section 2 describes the considered thresholding problem. Section 3 briefly describes the fundamentals of the existing MNDL subspace selection. Section 4 introduces the MNDL thresholding approach. Hard and soft MNDL thresholdings are presented in Sections 5 and 6. Section 7 provides the simulation results and Section 8 is our conclusion.
2. Problem Statement
Noiseless data  of length
of length  has been corrupted by an additive noise:
has been corrupted by an additive noise:

where  is an independent and identically distributed (i.i.d) Gaussian random process with zero mean and variance
is an independent and identically distributed (i.i.d) Gaussian random process with zero mean and variance  . (The method presented here is for real data. However, it can also be used for complex data. )In the considered denoising process, we project the noisy data into an orthogonal basis. The goal is to provide the optimum threshold for the resulting coefficients that minimizes the mean square error.
. (The method presented here is for real data. However, it can also be used for complex data. )In the considered denoising process, we project the noisy data into an orthogonal basis. The goal is to provide the optimum threshold for the resulting coefficients that minimizes the mean square error.
Assume that the noiseless data vector  is generated by space
is generated by space  . The space
. The space  can be expanded by orthogonal basis vectors:
can be expanded by orthogonal basis vectors:

where  is the inner product of vectors
is the inner product of vectors  and
and  .
.
The data in (1) is represented in this basis as follows:


where  is the
is the  th coefficient of the noiseless data,
th coefficient of the noiseless data,  is the
is the  -th coefficient of the noisy data, and
-th coefficient of the noisy data, and  is the
is the  -th coefficient of the additive noise. Note that since the basis vectors of
-th coefficient of the additive noise. Note that since the basis vectors of  are orthogonal,
are orthogonal,  is also a sample of Gaussian distribution with zero mean and variance,
is also a sample of Gaussian distribution with zero mean and variance,  .
.
The thresholding approach uses the available noisy coefficients,  , to provide the best estimate of the noiseless coefficients denoted by
, to provide the best estimate of the noiseless coefficients denoted by  . There are two general thresholding methods: hard and soft thresholdings. Hard thresholding eliminates or keeps the coefficients by comparing them with the threshold
. There are two general thresholding methods: hard and soft thresholdings. Hard thresholding eliminates or keeps the coefficients by comparing them with the threshold

where  is the hard threshold. Soft thresholding eliminates the coefficients below
is the hard threshold. Soft thresholding eliminates the coefficients below  and reduces the absolute value of the rest of the coefficients:
and reduces the absolute value of the rest of the coefficients:

There are different approaches for calculation of the proper  and
and  . In this paper, we expand the existing theory of the MNDL subspace selection method in [10] to provide new hard and soft thresholding methods.
. In this paper, we expand the existing theory of the MNDL subspace selection method in [10] to provide new hard and soft thresholding methods.
Important Notation
In this paper a random variable is denoted by a capital letter, such as  and
and  , while a sample of that random variable is represented by the same letter in lower case such as
, while a sample of that random variable is represented by the same letter in lower case such as  and
and  .
.
3. MNDL Subspace Selection (MNDL-SS)
The MNDL Subspace Selection (MNDL-SS) approach has been introduced in [10]. This approach addresses the problem of basis selection in the presence of a noisy data. In MNDL-SS, competing subspaces represent a projection of the noisy data on a complete orthogonal basis such as an orthogonal wavelet basis. each subspace contains a subset of the basis. The subspace keeps the coefficients of the noisy data in that subset and sets the rest of the coefficients to zero. Among competing subspaces, MNDL-SS chooses the subspace that minimizes the description length (codelength) of "noiseless" data. In this setting subspaces of the space  are chosen as follows: Each
are chosen as follows: Each  is a subspace of
is a subspace of  that is spanned by the first
that is spanned by the first  elements of the bases. The estimate of the noiseless coefficients in subspace
elements of the bases. The estimate of the noiseless coefficients in subspace  is
is

and the estimate of the noiseless data in  ,
,  , is
, is

In each subspace the description length (codelength) of the noiseless data is defined as [10] (this criterion is different from MDL criterion and the explanation is provided in [10])

where  is the reconstruction error (the equality of the error in the time domain and the error in coefficients of data is the result of the Parseval's Theorem):
is the reconstruction error (the equality of the error in the time domain and the error in coefficients of data is the result of the Parseval's Theorem):

which is a sample of random variable  .
.
The optimum subspace  can be chosen by minimizing the average description length of noiseless data among the competing subspaces. Minimizing the average of noiseless data length in (9) is equivalent to minimizing the mean square error (MSE) in the form of
can be chosen by minimizing the average description length of noiseless data among the competing subspaces. Minimizing the average of noiseless data length in (9) is equivalent to minimizing the mean square error (MSE) in the form of  as the term
as the term  is a constant and not a function of
is a constant and not a function of  :
:

MNDL-SS estimates the MSE for each subspace by using the available data error  in that subspace. The data error is defined in the following form:
in that subspace. The data error is defined in the following form:

which is a sample of random variable  . MNDL-SS studies the structure of the two random variables
. MNDL-SS studies the structure of the two random variables  and
and  and uses the connection between these two random variables to provide an estimate of the desired criterion
and uses the connection between these two random variables to provide an estimate of the desired criterion  for different
for different  .
.
4. MNDL Thresholding
To use the ideas of subspace selection in thresholding, we first have to explain how a particular choice of subspaces serves the problem of thresholding. In MNDL-SS, the competing subspaces are chosen a priori and are not functions of the observed data. However, if the method is going to be used for thresholding, forming the competing subspaces is based on the observed data. In this case, we first sort the bases based on the absolute value of the observed noisy coefficients  . This will dictate a particular indexing on the bases such that
. This will dictate a particular indexing on the bases such that

Therefore, the first subset represents the basis associated with the largest absolute value of the coefficients. The subset with two coefficients includes the two bases with the largest absolute value of the sorted coefficients and so on. The subspace  includes
includes  of the basis and represents the first
of the basis and represents the first  largest absolute values of the coefficients and as a result this subspace represents thresholding with a threshold value of
largest absolute values of the coefficients and as a result this subspace represents thresholding with a threshold value of  .
.
Back to the MNDL-SS, the subspace  that minimizes the average codelength of the noiseless data (equivalent to the subspace MSE in (11)) is the optimum subspace. Due to the indexing in the form of (13), the choice of this subspace results in the optimum threshold
that minimizes the average codelength of the noiseless data (equivalent to the subspace MSE in (11)) is the optimum subspace. Due to the indexing in the form of (13), the choice of this subspace results in the optimum threshold  .
.
To estimate the MSE of the subspaces, we follow the fundamentals of the MNDL-SS method. Due to the random choice of subspaces in MNDL-SS, the random variables  s that represent the additive noise of the coefficients in (4) are independent Gaussian random variables. In MNDL thresholding, the additive noise of coefficients is still Gaussian. However, due to the particular choice of the index for the coefficients,
s that represent the additive noise of the coefficients in (4) are independent Gaussian random variables. In MNDL thresholding, the additive noise of coefficients is still Gaussian. However, due to the particular choice of the index for the coefficients,  s are no longer independent. This will cause a major challenge in estimating the MSE of subspaces and is the main focus of this paper.
s are no longer independent. This will cause a major challenge in estimating the MSE of subspaces and is the main focus of this paper.
5. MNDL Hard Thresholding
In [10] it is shown that the expected value of the reconstruction error and that of the data error in subspace  can be written in the form of
can be written in the form of


where  is the
is the  -norm of the discarded coefficient vector in subspace
-norm of the discarded coefficient vector in subspace  :
:

and the noise parts are


where  is the Gaussian random variable with samples defined in (3).
is the Gaussian random variable with samples defined in (3).
If the noise parts  and
and  are available, then by estimating the expected value of the data error with the available sample
are available, then by estimating the expected value of the data error with the available sample  we have
we have

and then the estimate of the desired MSE in (14) is

The main challenge in MNDL thresholding is in calculating  and
and  in (18) and (17). In MNDL-SS, due to the independence of
in (18) and (17). In MNDL-SS, due to the independence of  s in (4), random variables
s in (4), random variables  and
and  are Chi-square random variables and calculation of the expected values of these terms is straight forward. However, in MDNL thresholding, since the
are Chi-square random variables and calculation of the expected values of these terms is straight forward. However, in MDNL thresholding, since the  s are not independent, calculation of these expected values is not easy. In the following section we focus on estimating these desired expected values for the case of thresholding.
s are not independent, calculation of these expected values is not easy. In the following section we focus on estimating these desired expected values for the case of thresholding.
5.1. Estimate of MSE in MNDL Hard Thresholding
In order to calculate the expected value of the additive noise in (17) and (18), we need to study the noise effects that are associated with the sorted noisy coefficients. Each  in (4) has a Gaussian distribution with mean
in (4) has a Gaussian distribution with mean  and variance
and variance  . Figure 1 shows the distribution of
. Figure 1 shows the distribution of  ,
,  , and
, and  . The expected value of the noise part of
. The expected value of the noise part of  under the condition
under the condition  is as follows:
is as follows:

where


and  is
is

where  and
and  and
and  are defined as
are defined as


Details of the calculation are provided in Appendix .
Therefore, for the desired noise parts we have


Similarly we have


The noise part of the MSE in (27) and the noise part of the expected value of data error in (29) are dependent on  ,
,  that are not available. We suggest estimating them by using the available data as follows [11].
that are not available. We suggest estimating them by using the available data as follows [11].
-
(i)
Generate
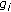 Gaussian vectors of data length with variance of the additive noise.
Gaussian vectors of data length with variance of the additive noise. -
(ii)
Sort the absolute value of the associated noise coefficients,
 .
. -
(iii)
Find the estimate of the expected value of this vector
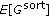 by averaging over 50 samples of these vectors:
by averaging over 50 samples of these vectors: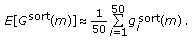 (31)
(31) -
(iv)
Estimate
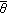 as follows:
as follows: (32)
(32)
-
(i)
Estimate
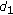 and
and 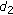 by replacing
by replacing  with
with  in (22) and (23):
in (22) and (23): (33)
(33)

The estimates of the noise parts in (27) and (29) are


5.2. Calculating the Threshold
By using the provided noise part estimates in (35) and (36) we can estimate the desired MSE for subsets of different order with the following steps.
-
(i)
Estimate the noise parts
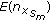 and
and  using (36) and (35).
using (36) and (35). -
(ii)
Estimate the MSE in (20) as follows:
 (37)
(37)
In MNDL thresholding the goal is to find  by minimizing the MSE in (11). Here we provide an estimate of
by minimizing the MSE in (11). Here we provide an estimate of  using the MSE estimate:
using the MSE estimate:

6. MNDL Soft Thresholding
In some applications, such as image denoising, soft thresholding generally performs better and provides a smaller MSE than hard thresholding [12]. In soft thresholding, not only are the values smaller than the threshold set to zero, but also the value of coefficients larger than the threshold is also reduced by the amount of the threshold. Thus, we need to take into account this changing level of coefficients in MSE estimation. For MNDL soft thresholding we follow the same procedure as in MNDL hard thresholding. Here, the MSE in subspace  is
is

where  is the smallest coefficient in subspace
is the smallest coefficient in subspace  (which is
(which is  ).
).
6.1. Noise Effects in the MSE
The noise part of the MSE in (39) is

where  s are the associated noise parts of coefficients
s are the associated noise parts of coefficients  s in subspace
s in subspace  . The expected value of the noise part of
. The expected value of the noise part of  under the condition
under the condition  is
is

where  and
and  are defined similar to those in (22) and (23), and
are defined similar to those in (22) and (23), and  is defined as
is defined as

where  and
and  are defined as
are defined as


Details of this calculation are provided in Appendix .
Using the estimates of  and
and  from (33) and (34), the estimate of MSE's noise part in (40) is
from (33) and (34), the estimate of MSE's noise part in (40) is

6.2. Estimate of the Noiseless Part of MSE
To complete the estimation of MSE in (39), we need also to estimate the noiseless part using the data error. The expected value of the data error in the case of soft thresholding is

(Details are provided in Appendix ). The last component is the same as noise part in MNDL hard thresholding in (29) and can be estimated by using (36). Therefore, by estimating  with its available sample
with its available sample  , from (46) we have
, from (46) we have

where  is defined in (24) and
is defined in (24) and  and
and  are defined in (33) and (34).
are defined in (33) and (34).
6.3. Calculating the Threshold
The two components of MSE in (39) were estimated in previous sections. Therefore, the MSE can be estimated as follows.
-
(i)
The noise part is estimated by using (45).
-
(ii)
The noiseless part is estimated by using (47).
-
(iii)
The estimate of the MSE in (39) is the sum of (45) and??(47):

Similar to MNDL hard thresholding, the optimum subspace is the one for which the estimate of the MSE is minimized:

6.4. Subband-Dependent MNDL Soft Thresholding
In image denoising, soft thresholding methods outperform hard thresholding methods in terms of MSE value and visual quality. In addition, it has been shown that subband-dependent thresholding performs better than universal thresholding methods [8]. In the subband-dependent method, a different threshold is provided for every subband of the wavelet transform. Here, we present the subband-dependent MNDL soft thresholding method. In every subband the MSE is estimated as a function of its subspaces. The subspace and its equivalent threshold that minimizes the MSE are chosen. The process of subband dependent MNDL thresholding with wavelet thresholds is as follows.
-
(i)
The discrete wavelet transform of the image is taken.
-
(ii)
In every subband the MSE, in (39), is estimated as a function of the
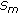 : the noise part is estimated using (45), and the noiseless part is estimated using (47). MSE estimate
: the noise part is estimated using (45), and the noiseless part is estimated using (47). MSE estimate 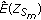 is the sum of the noiseless part and the noise part estimates.
is the sum of the noiseless part and the noise part estimates. -
(iii)
In each subband, the MSE is minimized over values of
 , and
, and 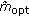 in (38) is chosen, where
in (38) is chosen, where  , and
, and  is the number of coefficients in the subband.
is the number of coefficients in the subband. -
(iv)
In each subband, the
 th largest absolute value of the coefficients is the optimum threshold.
th largest absolute value of the coefficients is the optimum threshold. -
(v)
The image is denoised using the subband thresholds.
-
(vi)
The inverse discrete wavelet transform is taken.
The unknown noise variance is estimated by the median estimator,  , where MAD is the median of absolute value of the wavelet coefficients at the finest decomposition level (the diagonal direction of decomposition level one).
, where MAD is the median of absolute value of the wavelet coefficients at the finest decomposition level (the diagonal direction of decomposition level one).
In the following section we provide simulation results of the method. The low complexity of this algorithm is an additional strength of the method. Our future plan is to utilize the approach for potential applications in areas such as biomedical engineering [13].
7. Simulation Results
We first demonstrate the performance of MNDL hard and soft thresholding by using two well-known examples in wavelet denoising. The first signal is the Blocks signal of length 1024 with few nonzero coefficients. The signal along with its wavelet coefficients is shown in Figure 2. Wavelet transform employs Daubechies's wavelet with eight vanishing moments with four scales of orthogonal decomposition [14]. The other signal is the Mishmash signal of length 1024 with no nonzero coefficients in Figure 3.
The MSE and its estimates using the existing MNDL-SS method [10] and the developed MNDL hard thresholding method are shown in Figure 4. The  that minimizes the unavailable MSE and its estimate,
that minimizes the unavailable MSE and its estimate,  , with these approaches are provided in Table 1 for different noise variances. The results in this table and the rest of the results in this section are averages of five runs. As the figure and the table show, as was expected MNDL thresholding outperforms the MNDL-SS approach.
, with these approaches are provided in Table 1 for different noise variances. The results in this table and the rest of the results in this section are averages of five runs. As the figure and the table show, as was expected MNDL thresholding outperforms the MNDL-SS approach.
 and its estimates using MNDL hard thresholding and MNDL-SS methods for the Blocks signal.
and its estimates using MNDL hard thresholding and MNDL-SS methods for the Blocks signal.Table 2 compares the MSE of the proposed hard thresholding method with that of two hard thresholding methods, VisuShrink and MDL. The comparison includes the optimum hard MSE, which represents the minimum MSE when the noisy coefficients are used as hard thresholds, along with the resulting MSE of different approaches. As the table shows, in most cases, MNDL hard thresholding provides the minimum MSE among the approaches.
The MSE and its estimate with MNDL soft thresholding are shown in Figure 5. The results in this figure are for Blocks and Mishmash signals and for two different levels of the additive noise. As the figure shows, MSE estimates are very close to the MSE itself.
The MSE results for soft threshoding are compared in Table 3. The table provides optimum MSE with both optimum thresholding and optimum subband thresholding along with the results for Sureshrink and MNDL soft thresholding. As the table shows for Blocks the MNDL subband-dependent has the best results while for Mishmash MNDL soft thresholding outperforms the other approaches in almost all cases. While here we have shown the simulation results for two of six test signals in [8], the results for the other two signals (Heavy sine, Doppler) are similar to those of the provided signals.
 Optimum soft thresholding;
Optimum soft thresholding;  Optimum Subband-dependent soft thresholding;
Optimum Subband-dependent soft thresholding;  MNDL soft thresholding,
MNDL soft thresholding,  MNDL Subband-dependent soft thresholding,
MNDL Subband-dependent soft thresholding,  Sureshrink.
Sureshrink.7.1. Image Denoising
There are many image denoising approaches, such as recent work in [15, 16]. These approaches have succeeded in providing good results. They usually use a particular assumption either on the noisy image and/or on the class of the data estimator. A well-known image denoising thresholding approach is BayesShrink. BayesShrink [12] is a thresholding method that is also widely used for image denoising. This method attempts to minimize the Bayes' Risk Estimator function assuming a prior Generalized Gaussian Distribution (GGD) and thus yields a data adaptive threshold [17]. Note that our method does not make any particular assumption on the data and is not especially proposed for image denoising. Here we use the approach for images as an example of a class of two-dimensional data.
To explore the application of MNDL soft thresholding in image denoising we use four images: Cameraman (a sample of a soft image), Barbara (a sample of a highly detailed image), Lena, and Peppers. These images are shown in Figure 6 and with size 512 512. The wavelet transform employs Daubechies's wavelet with eight vanishing moments and with four scales of orthogonal decomposition.
512. The wavelet transform employs Daubechies's wavelet with eight vanishing moments and with four scales of orthogonal decomposition.
In Table 4, we compare the MSE of the MNDL with two well-known thresholding methods: BayesShrink [12] and SureShrink [8]. All these thresholds are soft subband-dependent. As the table shows, MNDL thresholding performs better than SureShrink in most cases and is comparable with the BayesShrink. The MNDL soft thresholding is compared visually with BayesShrink and SureShrink in Figure 7. As the figure shows, the ringing effect at the edges of the image with the MNDL soft thresholding is less than that with the BayesShrink approach. The importance of the new approach is that it can provide an estimate of MSE simultaneously. Note that it can also provide estimate of MSE for other thresholding methods as follows. Find the closest absolute value of the coefficients to the given threshold and use the index  of that coefficient and check the estimate of MSE for the associated
of that coefficient and check the estimate of MSE for the associated  . Table 5 shows the optimum subband threshold for Cameraman and Table 6 shows the thresholds for BayesShrink and MNDL. As the tables show, the thresholds of MNDL are slightly larger than the optimum ones. On the other hand the Bayes thresholds are smaller than the optimum ones, especially for the coarsest level. While the MSE at this noise level is almost the same for these methods, the thresholds indicate that MNDL keeps fewer coefficients compared to BayesShrink and its threshold is much closer to the optimum one.
. Table 5 shows the optimum subband threshold for Cameraman and Table 6 shows the thresholds for BayesShrink and MNDL. As the tables show, the thresholds of MNDL are slightly larger than the optimum ones. On the other hand the Bayes thresholds are smaller than the optimum ones, especially for the coarsest level. While the MSE at this noise level is almost the same for these methods, the thresholds indicate that MNDL keeps fewer coefficients compared to BayesShrink and its threshold is much closer to the optimum one.
 Optimum soft MSE,
Optimum soft MSE,  MNDL soft thresholding,
MNDL soft thresholding,  BayesShrink, and
BayesShrink, and  SureShrink. Averaged over five runs.
SureShrink. Averaged over five runs. .
. .
.8. Conclusion
We proposed thresholding method based on the MNDL-SS approach. This approach uses the available data error to provide an estimate of the desired noiseless codelength for comparison of competing subspaces. In this approach, the statistics of the data error plays an important role. Unlike MNDL-SS, in MNDL thresholding the involved additive noises of the error are highly dependent. The main challenge of this work was to estimate the desired criterion in the presence of such dependence. We developed a method to estimate the desired criterion for the purpose of thresholding.
Experimental results show that the proposed MNDL hard thresholding method outperforms VisuShrink most of the time and the proposed MNDL soft thresholding method outperforms SureShrink most of the time. Application of MNDL soft thresholding for image denoising is also explored and the method proves comparable with the BayesShrink approach. Unlike the image denoising approaches, with MNDL thresholding no assumption on the structure of the signal is necessary. The main advantage of the method is in estimating both the desired noiseless description length and the mean square error (MSE). The calculated MSE estimate provides a quantitative quality measure for the proposed threshold simultaneously. An additional strength of the approach is its ability to estimate the MSE for any given threshold and it can be used for quality evaluation of any thresholding method.
References
Yang R, Yin L, Gabbouj M, Astola J, Neuvo Y: Optimal weighted median filtering under structural constraints. IEEE Transactions on Signal Processing 1995, 43(3):591-604. 10.1109/78.370615
Abramovich F, Sapatinas T, Silverman BW: Wavelet thresholding via a Bayesian approach. Journal of the Royal Statistical Society. Series B 1998, 60(4):725-749. 10.1111/1467-9868.00151
Chipman HA, Kolaczyk ED, McCulloch RE: Adaptive Bayesian wavelet shrinkage. Journal of the American Statistical Association 1997, 92(440):1413-1421. 10.2307/2965411
Clyde M, George EI: Flexible empirical Bayes estimation for wavelets. Journal of the Royal Statistical Society. Series B 2000, 62(4):681-698. 10.1111/1467-9868.00257
Sardy S: Minimax threshold for denoising complex signals with waveshrink. IEEE Transactions on Signal Processing 2000, 48(4):1023-1028. 10.1109/78.827536
Ben Hamza A, Luque-Escamilla PL, Martínez-Aroza J, Román-Roldán R: Removing noise and preserving details with relaxed median filters. Journal of Mathematical Imaging and Vision 1999, 11(2):161-177. 10.1023/A:1008395514426
Donoho DL, Johnstone IM: Ideal spatial adaption via wavelet shrinkage. Biometrika 1994, 81: 425-455. 10.1093/biomet/81.3.425
Donoho D, Johnstone IM: Adapting to unknown smoothness via wavelet shrinkage. Journal of the American Statistical Association 1995, 90: 1200-1224. 10.2307/2291512
Krim H, Tucker D, Mallat S, Donoho D: On denoising and best signal representation. IEEE Transactions on Information Theory 1999, 45(7):2225-2238. 10.1109/18.796365
Beheshti S, Dahleh MA: A new information-theoretic approach to signal denoising and best basis selection. IEEE Transactions on Signal Processing 2005, 53(10):3613-3624.
Fakhrzadeh A, Beheshti S: Minimum noiseless description length (MNDL) thresholding. Proceedings of the IEEE Symposium on Computational Intelligence in Image and Signal Processing (CIISP '07), 2007 146-150.
Chang SG, Yu B, Vetterli M: Adaptive wavelet thresholding for image denoising and compression. IEEE Transactions on Image Processing 2000, 9(9):1532-1546. 10.1109/83.862633
Krishnan S, Rangayyan RM: Automatic de-noising of knee-joint vibration signals using adaptive time-frequency representations. Medical and Biological Engineering and Computing 2000, 38(1):2-8. 10.1007/BF02344681
Daubechies I: Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. Volume 61. SIAM, Philadelphia, Pa, USA; 1992.
Luisier F, Blu T, Unser M: A new sure approach to image denoising: interscale orthonormal wavelet thresholding. IEEE Transactions on Image Processing 2007, 16(3):593-606.
Zhang M, Gunturk BK: Multiresolution bilateral filtering for image denoising. IEEE Transactions on Image Processing 2008, 17(12):2324-2333.
Mallat SG: Theory for multiresolution signal decomposition: the wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence 1989, 11(7):674-693. 10.1109/34.192463
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
A.  in Hard and Soft Thresholding
in Hard and Soft Thresholding
The expected value of the data error in hard thresholding, in (12), is


Since the noiseless coefficients  s are independent of the noise part
s are independent of the noise part  s, the third term becomes zero and we conclude with (15).
s, the third term becomes zero and we conclude with (15).
The expected value of the data error in soft thresholding is


The second part of the expected value of the data error in (A.4) is the same as the expected value of the data error in the hard thresholding in (A.1). Therefore, (A.4) can be written in the form of (46).
B. Calculating 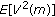 in MNDL Hard Thresholding
in MNDL Hard Thresholding
The distribution of noise coefficients is a Gaussian one and we have  . On the other hand, for a sorted version of coefficients we have
. On the other hand, for a sorted version of coefficients we have  while
while  . Therefore, the following extra condition holds on the noise coefficients:
. Therefore, the following extra condition holds on the noise coefficients:

Under the above condition, the desired conditional expected value is

where the numerator  is
is

and the denominator is

where  and
and  are
are


The conditional expectation of  in (B.2) can be simplified to
in (B.2) can be simplified to

where  ,
,  , and
, and  are defined in (22), (23), and (24).
are defined in (22), (23), and (24).
Any  in the paper is the conditional expectation in (B.2). For notation simplicity, the condition of the expectation is eliminated throughout the paper.
in the paper is the conditional expectation in (B.2). For notation simplicity, the condition of the expectation is eliminated throughout the paper.
C. Calculating 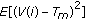 in MNDL Soft Thresholding
in MNDL Soft Thresholding
Similar to calculating the conditional expected value of  for MNDL hard thresholding, under the same condition
for MNDL hard thresholding, under the same condition  , we have
, we have

where the denominator is provided in (B.4) and the numerator is

There are three integrals in  . The first integral is
. The first integral is

The second integral is

and the third integral is

The numerator of (C.1) is calculated by adding up (C.3), (C.4) and (C.5). Therefore, the simplified version of  in (C.1) is
in (C.1) is

where  ,
,  , and
, and  are defined in (22), (23), and (42).
are defined in (22), (23), and (42).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Beheshti, S., Fakhrzadeh, A. & Krishnan, S. Noiseless Codelength in Wavelet Denoising. EURASIP J. Adv. Signal Process. 2010, 641842 (2010). https://doi.org/10.1155/2010/641842
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/641842

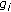 Gaussian vectors of data length with variance of the additive noise.
Gaussian vectors of data length with variance of the additive noise. .
.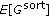 by averaging over 50 samples of these vectors:
by averaging over 50 samples of these vectors: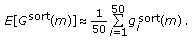
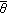 as follows:
as follows:
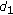 and
and 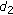 by replacing
by replacing  with
with  in (22) and (23):
in (22) and (23):
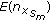 and
and  using (36) and (35).
using (36) and (35).
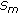 : the noise part is estimated using (45), and the noiseless part is estimated using (47). MSE estimate
: the noise part is estimated using (45), and the noiseless part is estimated using (47). MSE estimate 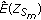 is the sum of the noiseless part and the noise part estimates.
is the sum of the noiseless part and the noise part estimates. , and
, and 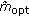 in (38) is chosen, where
in (38) is chosen, where  , and
, and  is the number of coefficients in the subband.
is the number of coefficients in the subband. th largest absolute value of the coefficients is the optimum threshold.
th largest absolute value of the coefficients is the optimum threshold.


 .
.


 in Hard and Soft Thresholding
in Hard and Soft Thresholding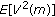 in MNDL Hard Thresholding
in MNDL Hard Thresholding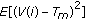 in MNDL Soft Thresholding
in MNDL Soft Thresholding