- Research Article
- Open access
- Published:
Two-Dimensional Beam Tracing from Visibility Diagrams for Real-Time Acoustic Rendering
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 642316 (2010)
Abstract
We present an extension of the fast beam-tracing method presented in the work of Antonacci et al. (2008) for the simulation of acoustic propagation in reverberant environments that accounts for diffraction and diffusion. More specifically, we show how visibility maps are suitable for modeling propagation phenomena more complex than specular reflections. We also show how the beam-tree lookup for path tracing can be entirely performed on visibility maps as well. We then contextualize such method to the two different cases of channel (point-to-point) rendering using a headset, and the rendering of a wave field based on arrays of speakers. Finally, we provide some experimental results and comparisons with real data to show the effectiveness and the accuracy of the approach in simulating the soundfield in an environment.
1. Introduction
Rendering acoustic sources in virtual environments is a challenging problem, especially when real-time operation is required without giving up a realistic impression of the result. The literature is rich with methods that approach this problem for a variety of purposes. Such methods are roughly divided into two classes: the former is based on an approximate solution of the wave equation on a finite grid, while the latter is based on the geometric modeling of acoustic propagation. Typical examples of the first class of methods are based on the solution of the Green's or Helmholtz-Kirchoff's equation through finite and boundary element methods [1–3]. The computational effort required by the solution of the wave equation, however, makes these algorithms unsuitable for real-time operation except for a very limited range of frequencies. Geometric methods, on the other hand, are the most widespread techniques for the modeling of early acoustic reflections in complex environments. Starting from the spatial distribution of the reflectors, their acoustic properties, and the location and the radiation characteristics of sources and receivers (listening points), geometric methods cast rays in space and track their propagation and interaction with obstacles in the environment [4]. The sequence of reflections, diffractions and diffusions a ray undergoes constitutes the acoustic path that link source and receiver.
Among the many available geometric methods, a particularly efficient one is represented by beam tracing [5–9]. This method was originally conceived by Hanrahan and Heckbert [5] for applications of image rendering, and was later extended by Funkhouser et al. [10] to the problem of audio rendering. A beam is intended as a bundle of acoustic rays originating from a point in space (a real source or a wall-reflected one), which fall onto the same planar portion of an acoustic reflector. Every time a beam encounters a reflector, in fact, it splits into a set of subbeams, each corresponding to a different planar region of that reflector or of some other reflector. As they bounce around in the environment, beams keep branching out. The beam-tracing method organizes and encodes this beam splitting/branching process into a specialized data structure called beam-tree, which describes the information of the visibility of a region from a point (i.e., the source location). Once the beam-tree is available, path-tracing becomes a very efficient process. In fact, given the location of the listening point (receiver), we can immediately determine which beams illuminate it, just through a "look up" of the beam-tree data structure. We should notice, however, that with this solution the computational effort associated to the beam tracing process and that of path-tracing are quite unbalanced. In fact if the environment is composed by  reflectors, the exhaustive test of the mutual visibility among all the
reflectors, the exhaustive test of the mutual visibility among all the  reflectors involves
reflectors involves  tests, while the test of the presence of the receiver in the
tests, while the test of the presence of the receiver in the  traced beams needs only
traced beams needs only  tests. Some solutions for a speedup of the computation of the beam-tree have been proposed in the literature. As an example in [10] the authors adopt the Binary Space Partitioning Technique to operate a selection of the visible obstacles from a prescribed reflector. A similar solution was recently proposed in [11], where the authors show that a real-time tracing of acoustic paths is possible even in a simple dynamic environment.
tests. Some solutions for a speedup of the computation of the beam-tree have been proposed in the literature. As an example in [10] the authors adopt the Binary Space Partitioning Technique to operate a selection of the visible obstacles from a prescribed reflector. A similar solution was recently proposed in [11], where the authors show that a real-time tracing of acoustic paths is possible even in a simple dynamic environment.
In [12] the authors generalized traditional beam tracing by developing a method for constructing the beam-tree through a lookup on a precomputed data structure called global visibility function, which describes the visibility of a region not just as a function of the viewing angle but also of the source location itself.
Early reflections are known to carry some information on the geometry of the surrounding space and on the spatial positioning of acoustic sources. It is in the initial phase of reverberation, in fact, that we receive the echoes associated to the first wall reflections. Other propagation phenomena, such as diffusion, transmission and diffraction tend to enrich the sense of presence in "virtual walkthrough" scenarios, especially in densely occluded environments. As beam tracing was originally conceived for the modeling of specular reflections only, some extensions of this method were proposed to account for other propagation phenomena. Funkhouser et al. [13], for example, account for diffusion and diffraction through a bidirectional beam tracing process. When the two beam-trees that originate from the receiver and the source intersect on specific geometric primitives such as edges and reflectors, propagation phenomena such as diffusion and diffraction could take place. The need of computing two beam-trees, however, poses problems of efficiency when using conventional beam tracing methods, particularly when sources and/or receivers are in motion. A different approach was proposed by Tsingos et al. [14], who proposed to use the uniform theory of diffraction (UTD) [15] by building secondary beam-trees originated from the diffractive edges. This approach is quite efficient, as the tracing of the diffractive beam-trees can be based on the sole geometric configuration of reflectors. Once source and receiver locations are given, in fact, a simple test on the diffractive beam-trees determines the diffractive paths. Again, however, this approach inherits the advantages of beam tracing but also its limits, which are in the fact that a new beam-tree needs be computed every time a source moves.
As already mentioned above, in [12] we proposed a method for generating a beam-tree through a lookup on the global visibility function. That method had the remarkable advantage of computing a large number of acoustic paths in real time as both source and reflector are in motion in a complex environment. In this paper we generalize the work proposed in [12] in order to accommodate diffusion and diffraction phenomena. We do so by revisiting the concept of global visibility and by introducing novel lookup methods and new operators. Thanks to these generalizations, we will also show how it is possible to work on the visibility diagrams not just for constructing beam-trees but also to perform the whole path-tracing process.
In this paper we expand and repurpose the beam tracing method for applications of real-time rendering of acoustic sources in virtual environments. Two are the envisioned scenarios: in the former the user is wearing a headset, in the latter the whole sound field within a prescribed volume is rendered using loudspeaker arrays. We will show that the two scenarios share the same beam tracing engine which, in the first case, is followed by a path-tracing algorithm based on beam-tree lookup [12], with an additional head-related transfer function. In the second case the beam tracer is used for generating the control parameters of the beam-shaping algorithm proposed in [16]. This beam-shaping method allows us to design the spatial filter to be applied to the loudspeaker arrays for the rendering of an arbitrary beam. Other solutions exist in the literature for the rendering of virtual environments, such as wave field synthesis (WFS) and ambisonics. Roughly speaking, WFS computes the spatial filter to be applied to the speakers with an approximation of the Helmholtz-Kirchoff's equation. Interestingly enough, for example, in [17] the task of computing the parameters of all the virtual sources in the environment is demanded to an image-source algorithm. Therefore, some WFS systems already partially rely on geometric methods. When rendering occluded environments, however, the image-source method tends to become computationally demanding, while fast beam tracing techniques [12] can offer a significant speedup.
It is important to notice that the method proposed in [12] was developed for modeling complex acoustic reflections in a specific class of 3D environments obtained as the cartesian product between a 2D floor plan and a 1D (vertical) direction. This situation, for example, describes a complex distribution of vertical walls ending in horizontal floor and ceiling. When considering acoustic wall transmission, a 2D  1D environment becomes useful for modeling a multi-floored building with a repeated floor plan. Although 2D
1D environment becomes useful for modeling a multi-floored building with a repeated floor plan. Although 2D  1D environments enjoy the advantages of 2D modeling (simplicity, duality, etc.), the computation of all delays and path lengths still needs to be performed in a 3D space. While this is rather straightforward in the case of geometric reflections, it becomes more challenging when dealing with diffraction and diffusion phenomena.
1D environments enjoy the advantages of 2D modeling (simplicity, duality, etc.), the computation of all delays and path lengths still needs to be performed in a 3D space. While this is rather straightforward in the case of geometric reflections, it becomes more challenging when dealing with diffraction and diffusion phenomena.
The paper is organized as follows. In Section 2 we review and revisit the concept of global visibility and its use for efficiently tracing acoustic paths. In Section 3 we discuss the main mathematical models used for explaining diffusion and diffraction phenomena, and we choose the one that best suits our beam tracing approach. Sections 4 and 5 focus on the modeling of diffusion and diffraction with visibility diagrams. In Section 6 we present two possible applications of the algorithm presented in this paper. In Section 7 we prove the efficiency and the effectiveness of our modeling solution. Finally, Section 8 provides some final comments and conclusions.
2. The Visibility Diagram Revisited
In this section we review the concept of visibility diagram, as it is a key element for the remainder of this paper. In [12] we adopted this representation for generating a specialized data structure that could swiftly provide information on how to trace acoustic beams and rays in real time with the rules of specular reflection. This approach constitutes a generalization of the beam tracing algorithm proposed by Hanrahan and Heckbert [5]. The visibility diagram is a re-mapping of the geometric structures and functional elements that constitute the geometric world (rays, beams, reflectors, sources, receivers, etc.) onto a special parameter space that is completely dual to the geometric one. Visibility diagrams are particularly useful for immediately assessing what is in the line of sight from a generic location and direction in space. We will first recount the basic concepts of visibility diagrams and provide a general view of the path-tracing problem for the specific case of purely specular reflections. This overview will be provided in a slightly more general fashion than in [12], as all the algorithmic steps will be given with reference to visibility diagrams, and will constitute the starting point for the discussions in the following sections.
2.1. Visibility and the Tracing Problem
A ray in a 2D space is uniquely characterized by three parameters: two for the location of its origin, and one for its direction. As we are tracing paths during their propagation, we are interested in rays emerging from a reflector after bouncing off it. As a consequence, the origin corresponds to the virtual source. Furthermore, because we are interested in assessing only where the ray will end up, we can afford ignoring some information on where the ray is coming from, for example the source distance. This means that a ray description based on three parameters turns out to be redundant, and can be easily reduced to two parameters. In [12] we adopted the Reference Reflector Parametrization (RRP) parametrization based on the location of the intersection on the reference reflector and the travel direction of the ray. Although the RRP is referred to a frame attached to a specific reflector, this choice does not represent a limitation, due to the iterative nature of the visibility evaluation process. Let  be the reference reflector. For reasons that will be clearer later on, the RRP normalizes
be the reference reflector. For reasons that will be clearer later on, the RRP normalizes  through a translation, a rotation and a scaling of the axes in such a way that the reference reflector lies on the segment of the
through a translation, a rotation and a scaling of the axes in such a way that the reference reflector lies on the segment of the  -axis between
-axis between  and 1. The set of rays passing through
and 1. The set of rays passing through  is described by the equation
is described by the equation  . Figure 1 shows the reflector
. Figure 1 shows the reflector  referred to the normalized frame in the geometric domain (left). The set of rays passing through
referred to the normalized frame in the geometric domain (left). The set of rays passing through  is called region of visibility from
is called region of visibility from  and it is represented by the horizontal strip (reference visibility strip) in the
and it is represented by the horizontal strip (reference visibility strip) in the  domain. Due to the duality between primitives in
domain. Due to the duality between primitives in  and
and  domains we will sometimes refer to the RRP as the dual space. We are interested in representing the mutual occlusions between reflectors in the dual space. With this purpose in mind, we split the visibility strip into visibility regions, each corresponding to the set of rays that hit the same reflector. According to the image-source principle, all the obstacles that lie in the same half space of the image-source, are discarded during the visibility test. As a convention, in the future we will use the rotation of the reference reflector which brings the image-source in the half-space
domains we will sometimes refer to the RRP as the dual space. We are interested in representing the mutual occlusions between reflectors in the dual space. With this purpose in mind, we split the visibility strip into visibility regions, each corresponding to the set of rays that hit the same reflector. According to the image-source principle, all the obstacles that lie in the same half space of the image-source, are discarded during the visibility test. As a convention, in the future we will use the rotation of the reference reflector which brings the image-source in the half-space  . The above parameter space turns out to play a similar role as the dual of a geometric space. In Table 1 we summarize the representation of some geometric primitives in the parameter space. A complete derivation of the relations of Table 1 can be found in [12, 18]. Notice that the relation between primitives in the two domains is of complete duality. For example, the dual of the oriented reflector is a wedge in the
. The above parameter space turns out to play a similar role as the dual of a geometric space. In Table 1 we summarize the representation of some geometric primitives in the parameter space. A complete derivation of the relations of Table 1 can be found in [12, 18]. Notice that the relation between primitives in the two domains is of complete duality. For example, the dual of the oriented reflector is a wedge in the  domain (sort of an oriented "beam" in parameter space). Conversely, the dual of an oriented beam (a single wedge in the
domain (sort of an oriented "beam" in parameter space). Conversely, the dual of an oriented beam (a single wedge in the  geometric space) is an oriented segment in the
geometric space) is an oriented segment in the  domain (sort of an oriented "reflector" in parameter space).
domain (sort of an oriented "reflector" in parameter space).
2.1.1. Visibility Region
The parameters describing all rays originating from the reference reflector  form the region of visibility from that reflector. After normalization, this region takes on the strip-like shape described in Figure 1, which we refer to as "reference visibility strip". Those rays that originate from the reference reflector and hit another reflector
form the region of visibility from that reflector. After normalization, this region takes on the strip-like shape described in Figure 1, which we refer to as "reference visibility strip". Those rays that originate from the reference reflector and hit another reflector  form a subset of this strip (see Figure 1) which corresponds to the intersection between the dual of
form a subset of this strip (see Figure 1) which corresponds to the intersection between the dual of  and the dual of
and the dual of  (reference visibility strip). The intersection of the dual of
(reference visibility strip). The intersection of the dual of  and the visibility strip is the visibility region of
and the visibility strip is the visibility region of  from
from  . Once the source location is specified, the set of rays passing through
. Once the source location is specified, the set of rays passing through  and
and  and departing from that location will be a subset of the visibility region of
and departing from that location will be a subset of the visibility region of  . One key advantage of the visibility approach to the beam tracing problem resides in the fact that we only need geometric information about the environment to compute the visibility regions, which can therefore be computed in advance.
. One key advantage of the visibility approach to the beam tracing problem resides in the fact that we only need geometric information about the environment to compute the visibility regions, which can therefore be computed in advance.
2.1.2. Dual of Multiple Reflectors: Visibility Diagrams
When there are more than two reflectors in the environment, we need to consider the possibility of mutual occlusions, which results in overlapping visibility regions. Sorting out which reflector occludes which (with respect to the reference reflector) corresponds to determining which visibility region overrides which in their overlap. Two solutions for the occlusion problem are possible: the first, already presented in [12], is based on a simple test in the geometric domain. An arbitrary ray chosen in the overlap of visibility regions can be cast to evaluate the front-to-back ordering of visibility regions or, more simply, to determine which oriented reflector is first met by the test ray. An example is provided in Figure 2 where, if  is the reference reflector, we end up having an occlusion between
is the reference reflector, we end up having an occlusion between  and
and  , which needs to be sorted out. A test ray is picked at random within the overlapping region to determine which reflector is hit first by the ray. This particular example shows that, unless we consider each reflector as the combination of two of oppositely-facing oriented reflectors, we cannot be sure that the occlusion problem can be disambiguated. In this case, for example,
, which needs to be sorted out. A test ray is picked at random within the overlapping region to determine which reflector is hit first by the ray. This particular example shows that, unless we consider each reflector as the combination of two of oppositely-facing oriented reflectors, we cannot be sure that the occlusion problem can be disambiguated. In this case, for example,  occludes
occludes  for some rays, and
for some rays, and  occludes
occludes  for others. As shown in Table 1, a two-sided reflector corresponds to a double wedge in ray space, each wedge corresponding to one of the two faces of the reflector. By considering the two sides of each reflector as individual oriented reflectors, we end up with four distinct wedge-like regions in ray space, thus removing all ambiguities. The overlap between visibility regions of two one-sided reflectors arises every time the extreme lines of the corresponding visibility regions intersect. We recall that the dual of a point
for others. As shown in Table 1, a two-sided reflector corresponds to a double wedge in ray space, each wedge corresponding to one of the two faces of the reflector. By considering the two sides of each reflector as individual oriented reflectors, we end up with four distinct wedge-like regions in ray space, thus removing all ambiguities. The overlap between visibility regions of two one-sided reflectors arises every time the extreme lines of the corresponding visibility regions intersect. We recall that the dual of a point  is a line whose slope is
is a line whose slope is  . The extreme lines of the visibility region of reflector
. The extreme lines of the visibility region of reflector  are the dual of the endpoints of
are the dual of the endpoints of  , that are
, that are  and
and  and the slopes of the extreme lines of the visibility region of
and the slopes of the extreme lines of the visibility region of  are
are  and
and  . A similar notation is used for the overlapping reflector
. A similar notation is used for the overlapping reflector  . Under the assumption that
. Under the assumption that  and
and  never intersect in the geometric domain, we can reorder one-sided reflectors in front-to-back order by simply looking at the slopes of the extreme lines of their visibility regions. If the line
never intersect in the geometric domain, we can reorder one-sided reflectors in front-to-back order by simply looking at the slopes of the extreme lines of their visibility regions. If the line  of equation
of equation  and the line
and the line  of equation
of equation  intersect in the dual space, then
intersect in the dual space, then  guarantees that
guarantees that  occludes
occludes  and
and  guarantees that
guarantees that  occludes
occludes  .
.
2.2. Tracing Reflective Beams and Paths in Dual Space
2.2.1. Tracing Beams
In this paragraph we summarize the tracing of beams in the geometric space using the information contained in the visibility diagrams. Further details on this specific topic can be found in [12]. This can be readily done by scanning the visibility diagram along the line that represents the "dual" of the virtual source. In fact, that line will be partitioned into a number of segments, one per visibility region. Each segment will correspond to a subbeam in the geometric space. Consider the configuration of reflectors of Figure 3(a). The first step of the algorithm consists of determining how the complete pencil of rays produced by the source  is partitioned into beams. This is done by evaluating the visibility from the source using traditional beam tracing. This initial splitting process produces two classes of beams: those that fall on a reflector and those that do not. The beams and the corresponding beam-tree are shown in Figures 3(a) and 3(b), respectively. We consider the splitting of beam
is partitioned into beams. This is done by evaluating the visibility from the source using traditional beam tracing. This initial splitting process produces two classes of beams: those that fall on a reflector and those that do not. The beams and the corresponding beam-tree are shown in Figures 3(a) and 3(b), respectively. We consider the splitting of beam  , shown in Figure 4. The image-source is represented in the dual space by the line
, shown in Figure 4. The image-source is represented in the dual space by the line  . The beam
. The beam  will therefore be a segment on that line, which will be partitioned in a number of segments, one for each region on the visibility diagram. In Figure 4(a) the beam splitting is accomplished in the
will therefore be a segment on that line, which will be partitioned in a number of segments, one for each region on the visibility diagram. In Figure 4(a) the beam splitting is accomplished in the  domain, while in Figure 4(b) we can see the corresponding subbeams in the geometric domain. This process is iterated for all the beams that fall onto a reflector. Further details can be found in [12]. At the end of the beam tracing process we end up with a tree-like data structure, each node
domain, while in Figure 4(b) we can see the corresponding subbeams in the geometric domain. This process is iterated for all the beams that fall onto a reflector. Further details can be found in [12]. At the end of the beam tracing process we end up with a tree-like data structure, each node  of which contains information that identifies the corresponding beam:
of which contains information that identifies the corresponding beam:
-
(i)
the one-sided reference reflector
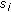 ,
, -
(ii)
the one-sided illuminated reflector
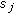 (if any),
(if any), -
(iii)
the position of the virtual source
 in the normalized reference frame,
in the normalized reference frame, -
(iv)
the segment
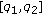 that identifies the "illuminating" region on the
that identifies the "illuminating" region on the 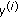 -axis,
-axis, -
(v)
the parent node (if any),
-
(vi)
a list of the children nodes (if at least one exists).
(a) Beam subdivision performed in the (m,q)domain for the bundle of rays corresponding to the reflection of the beam  of Figure 3. (b) Corresponding subbeams in the geometric domain.
of Figure 3. (b) Corresponding subbeams in the geometric domain.
The last two items are useful when reclaiming the "reflection history" of a beam. Given the above information we are immediately able to represent the beams (i.e., segments) in the  domain.
domain.
2.2.2. Tracing Paths
In [12] the construction of the beam-tree was accomplished in the dual space but path-tracing was entirely done in the geometric domain. We will now derive an alternate and more efficient procedure for tracing the acoustic paths directly in the dual space. The goal is to test the presence of the receiver  in the beam
in the beam  , originating from the reflector
, originating from the reflector  . The coordinates of the receiver in the normalized reference frame of
. The coordinates of the receiver in the normalized reference frame of  are
are  . In order for
. In order for  to be in
to be in  , there must exist a ray in
, there must exist a ray in  that passes through
that passes through  , that is,
, that is,

This means that the ray  from
from  to
to  , is represented in the dual space by a point resulting from the intersection of the dual of
, is represented in the dual space by a point resulting from the intersection of the dual of  (a segment) and the dual of
(a segment) and the dual of  (a line). The presence test is thus performed by computing the intersection of two lines in the parameter space. If
(a line). The presence test is thus performed by computing the intersection of two lines in the parameter space. If  does not fall onto a reflector, then the condition (1) is sufficient. If
does not fall onto a reflector, then the condition (1) is sufficient. If  falls on reflector
falls on reflector  , then we must also make sure that
, then we must also make sure that  does not occlude
does not occlude  . Assuming that
. Assuming that  lies on the line
lies on the line  , we can easily conclude that
, we can easily conclude that  is not occluded by
is not occluded by  if the distance between
if the distance between  and
and  is smaller than the distance between
is smaller than the distance between  and the intersection of the
and the intersection of the  ray with
ray with  , which means that:
, which means that:

The conditions in (1) and (possibly) (2) are tested for all the beams. However, if  falls onto
falls onto  , then we know that it cannot fall in other beams that share the virtual source of
, then we know that it cannot fall in other beams that share the virtual source of  . This speeds up the path-tracing process a great deal. As an example of the tracing process, consider the situation shown in Figure 5. Here
. This speeds up the path-tracing process a great deal. As an example of the tracing process, consider the situation shown in Figure 5. Here  and
and  are not in the line of sight, but a reflective path exists through the reflection from
are not in the line of sight, but a reflective path exists through the reflection from  . First-order beams are traced directly in the geometric domain, as done in [12], therefore the presence of
. First-order beams are traced directly in the geometric domain, as done in [12], therefore the presence of  in beams originating directly from
in beams originating directly from  is tested directly in the geometric domain. Let us now test the presence of
is tested directly in the geometric domain. Let us now test the presence of  in the reflected beams emerging from
in the reflected beams emerging from  (see Figure 3). The intersection between the line
(see Figure 3). The intersection between the line  , dual of
, dual of  , and the dual of
, and the dual of  (a segment) is easily found (see Figure 6 on the right). Once we have checked the presence of the receiver in
(a segment) is easily found (see Figure 6 on the right). Once we have checked the presence of the receiver in  , the position of the receiver and the information encoded in
, the position of the receiver and the information encoded in  are sufficient to determine the delay and the amplitude of the echo associated to that acoustic path. More details on this aspect will be provided in Section 6.1.
are sufficient to determine the delay and the amplitude of the echo associated to that acoustic path. More details on this aspect will be provided in Section 6.1.
Path-tracing from source Sto the receiver R. The beam-tree on the right-hand side is the same as in Figure 3.
3. Mathematical Models of Diffraction and Diffusion
In this section we investigate some mathematical models used in the literature to quantitatively describe the causes of diffraction and diffusion. Later we will choose the model which best works for our beam tracing method.
3.1. Models of Diffusion
When a wavefront encounters a rough or nonhomogeneous surface, its energy is diffused in nonspecular directions (see Figure 7). Let us consider a flat surface with a single localized unevenness whose size is bigger than the wavelength  of the incident wavefront. The Huygens principle interprets the diffused wavefront as the superposition of the local wavefronts associated to reflections on each point of the surface. As we can see in Figure 7, the direction of propagation of the outgoing wavefront differs from the direction of the incident one. Consequently, a sensor facing the wall will pick up energy not just from the incident wavefront but also from a direction that is not specular. A rough surface can be characterized through a statistical description of the speckles (in terms of size and density). In fact, the acoustic properties of the scattering material can be predicted or measured using various techniques [19–21]. Diffusion can also be associated to local variations of impedance (e.g., a flat reflective surface that exhibits areas of acoustically absorbing material) [22]. From the listener's standpoint, diffusion tends to greatly increase the number of paths between source and receiver and, consequently, the sense of presence [23]. Different models have been proposed in the literature to account for diffusion. A reflection is said to be totally diffusive (Lambertian) if the probability density function of the direction of the outgoing rays does not depend on the direction of the incoming ray. Totally diffused reflections are described by Lambert's cosine law. A survey on the typical acoustic characteristics of materials, however, reveals that Lambertian reflections turn out to be quite unrealistic. For this reason, in the literature we find two modeling descriptions: the scattering coefficient and the diffusion coefficient [24, 25]. The diffusion coefficient measures the similarity between the polar response of a Lambertian reflection and the actual one. This coefficient is expressed as the correlation index between the actual and the diffusive polar responses corresponding to a wavefront coming from a perpendicular direction with respect to the surface. The scattering coefficient measures the ratio between the energy diffused in nonspecular directions and the total (specular and diffused) reflected energy. This parameter is useful when we are interested in modeling diffusion in reverberant enclosures but it does not account for the directions of the diffused wavefronts. This approximation is reasonable in the presence of a large number of diffusive reflections, but tends to become a bit restrictive when considering first-order diffusion only (i.e., ignoring diffusion of diffused paths). This is why in this paper we consider the additional assumption that diffusive surfaces be wide. This way the range of directions of diffused propagation turns out to be wide enough to minimize the impact of the above approximation. We will use the scattering coefficient to weight the contribution coming from totally diffuse reflections (modeled by Lambert's cosine law) and specular reflections.
of the incident wavefront. The Huygens principle interprets the diffused wavefront as the superposition of the local wavefronts associated to reflections on each point of the surface. As we can see in Figure 7, the direction of propagation of the outgoing wavefront differs from the direction of the incident one. Consequently, a sensor facing the wall will pick up energy not just from the incident wavefront but also from a direction that is not specular. A rough surface can be characterized through a statistical description of the speckles (in terms of size and density). In fact, the acoustic properties of the scattering material can be predicted or measured using various techniques [19–21]. Diffusion can also be associated to local variations of impedance (e.g., a flat reflective surface that exhibits areas of acoustically absorbing material) [22]. From the listener's standpoint, diffusion tends to greatly increase the number of paths between source and receiver and, consequently, the sense of presence [23]. Different models have been proposed in the literature to account for diffusion. A reflection is said to be totally diffusive (Lambertian) if the probability density function of the direction of the outgoing rays does not depend on the direction of the incoming ray. Totally diffused reflections are described by Lambert's cosine law. A survey on the typical acoustic characteristics of materials, however, reveals that Lambertian reflections turn out to be quite unrealistic. For this reason, in the literature we find two modeling descriptions: the scattering coefficient and the diffusion coefficient [24, 25]. The diffusion coefficient measures the similarity between the polar response of a Lambertian reflection and the actual one. This coefficient is expressed as the correlation index between the actual and the diffusive polar responses corresponding to a wavefront coming from a perpendicular direction with respect to the surface. The scattering coefficient measures the ratio between the energy diffused in nonspecular directions and the total (specular and diffused) reflected energy. This parameter is useful when we are interested in modeling diffusion in reverberant enclosures but it does not account for the directions of the diffused wavefronts. This approximation is reasonable in the presence of a large number of diffusive reflections, but tends to become a bit restrictive when considering first-order diffusion only (i.e., ignoring diffusion of diffused paths). This is why in this paper we consider the additional assumption that diffusive surfaces be wide. This way the range of directions of diffused propagation turns out to be wide enough to minimize the impact of the above approximation. We will use the scattering coefficient to weight the contribution coming from totally diffuse reflections (modeled by Lambert's cosine law) and specular reflections.
3.2. Models of Diffraction
Diffraction is a very important propagation mode, particularly in densely occluded environments. Failing to properly account for this phenomenon in such situations could result in a poorly realistic rendering or even in annoying auditory artifacts. In this section we provide a brief description of three techniques for rendering diffraction phenomena: the Fresnel Ellipsoid, the line of sources, and the Uniform Theory of Diffraction (UTD). We will then explain why the UTD turns out to be the most suitable approach to the modeling of diffraction in conjunction with beam tracing.
3.2.1. Fresnel Ellipsoids
Let us consider a source  and a receiver
and a receiver  with an occluding obstacle in between. According to the Fresnel-Kirchhoff theory, the portion of the wavefront that is occluded by the obstacle does not contribute to the signal measured in
with an occluding obstacle in between. According to the Fresnel-Kirchhoff theory, the portion of the wavefront that is occluded by the obstacle does not contribute to the signal measured in  , which therefore differs from what we would have with unoccluded spherical propagation. In order to avoid using the Fresnel-Kirchhoff integral, we can adopt a simpler approach based on Fresnel ellipsoids. If
, which therefore differs from what we would have with unoccluded spherical propagation. In order to avoid using the Fresnel-Kirchhoff integral, we can adopt a simpler approach based on Fresnel ellipsoids. If  is the distance between
is the distance between  and
and  , only objects lying on paths whose length is between
, only objects lying on paths whose length is between  and
and  are considered as obstacles, where
are considered as obstacles, where  is the wavelength. If
is the wavelength. If  is the generic location of the secondary source, the locus of points that satisfy the equation
is the generic location of the secondary source, the locus of points that satisfy the equation  is an ellipsoid with foci in
is an ellipsoid with foci in  and
and  . The portion of the ellipsoid that is occluded by obstacles provides an estimate of the absolute value of the diffraction filter's response. It is important to notice that the size of the Fresnel ellipsoid depends on the signal wavelength. As a consequence, in order to study diffraction in a given configuration, we need to estimate the occluded portion of the Fresnel ellipsoids at the frequencies of interest. In [26] the author proposes to use the graphics hardware to estimate the hidden portions of the ellipsoids. The main limit related to the Fresnel ellipsoid is the absence of information related to the phase of the signal: from the hidden portions of the ellipsoid, in fact, we can only infer the absolute value of the diffraction filter. If we need a more accurate rendering of diffraction, we must resort to other techniques.
. The portion of the ellipsoid that is occluded by obstacles provides an estimate of the absolute value of the diffraction filter's response. It is important to notice that the size of the Fresnel ellipsoid depends on the signal wavelength. As a consequence, in order to study diffraction in a given configuration, we need to estimate the occluded portion of the Fresnel ellipsoids at the frequencies of interest. In [26] the author proposes to use the graphics hardware to estimate the hidden portions of the ellipsoids. The main limit related to the Fresnel ellipsoid is the absence of information related to the phase of the signal: from the hidden portions of the ellipsoid, in fact, we can only infer the absolute value of the diffraction filter. If we need a more accurate rendering of diffraction, we must resort to other techniques.
3.2.2. Line of Sources
In [27] the authors propose a framework for accurately quantifying diffraction phenomena. Their approach is based on the fact that each point on a diffractive edge receives the incident ray and then re-emits a muffled version of it. The edge can therefore be seen as a line of secondary sources. The acoustic wave that reaches the receiver will then be a weighed superposition of all wavefronts produced by such edge sources.
In order to quantitatively determine the impact of diffraction in closed form, we need to be able to evaluate the visibility of a region (environment) from a line (edge of secondary sources). As far as we know, there are no results in the literature concerning the evaluation of regional visibility from a line. There are, however, several works that simplify the problem by sampling the line of sources. This way, visibility is evaluated from a finite number of points [28–30]. This last approach can be readily accommodated into our framework. However, as we are interested in a fast rendering of diffraction, we prefer to look into alternate formulations.
3.2.3. Uniform Theory of Diffraction
The Uniform Theory of Diffraction (UTD) was derived by Kouyoumjian and Pathak [15] from the Geometric Theory of Diffraction (GTD), proposed by Keller in 1962 [31]. As shown in Figure 8, according to the GTD, an acoustic ray that falls onto an edge with an angle  produces a distribution of rays that lies on the surface of a cone. The axis of this cone is the edge itself, and its angle of aperture is
produces a distribution of rays that lies on the surface of a cone. The axis of this cone is the edge itself, and its angle of aperture is  . The GTD assumes that the edge be of infinite extension, therefore, given a source and a receiver we can always find a point on the edge such that the diffracted path that passes through it will satisfy the constraint
. The GTD assumes that the edge be of infinite extension, therefore, given a source and a receiver we can always find a point on the edge such that the diffracted path that passes through it will satisfy the constraint  . The Keller cones for the source
. The Keller cones for the source  and two points
and two points  and
and  on the edge are shown in Figure 8.
on the edge are shown in Figure 8.
Geometric Theory of Diffraction: an acoustic source is in S. The acoustic source interacts with the obstacle, producing diffracted rays. Given the source position S, the points on the edge behave as secondary sources (e.g.,  and
and  in the figure). According to the geometrical theory of diffraction, the angle between the outgoing rays and the edge equals the angle between the incoming ray and the edge. The envelope of the outgoing rays forms a cone, known in the literature as Keller cone.
in the figure). According to the geometrical theory of diffraction, the angle between the outgoing rays and the edge equals the angle between the incoming ray and the edge. The envelope of the outgoing rays forms a cone, known in the literature as Keller cone.
In a way, the GTD allows us to compactly account for all contributions of a line distribution of sources. In fact, if we were to integrate all the infinitesimal contributions over an infinite edge, we would end up with only one significant path, which is the one that complies with the Keller condition, as all the other contributions would end up canceling each other out. The impact of diffraction on the source signal is rendered by a diffraction coefficient that depends on the frequency and on the angle between the incident ray and the angular aperture of the diffracting wedge (see Section 6.1 and [32] for further details). This geometric interpretation of diffraction is also adopted by the UTD. The difference between GTD and UTD is in how such diffraction coefficients are computed (see Section 6.1).
The use of the UTD in beam tracing is quite convenient as it only involves one incident ray per diffractive path. The UTD, however, assumes that the wedge be of infinite extension and perfectly reflective, which in some cases is too strong an assumption. Nonetheless, the advantages associated to considering only the shortest path make the UTD an ideal framework for accounting for diffraction in beam tracing applications. Notice that when the incident ray is orthogonal to the edge ( ), the conic surface flattens onto a disc. This particular situation would be of special interest to us if we were considering an inherently 2D geometry. This, however, is NOT our case. We are, in fact, considering the situation of "separable" 3D environments [12], which result from the cartesian product between a 2D environment (floor map) and a 1D (vertical) direction. This special geometry (sort of an extruded floor map) requires the modeling of diffraction and diffusion phenomena in a 3D space. The Uniform Theory of Diffraction is, in fact, inherently three-dimensional, but our approach to the tracing of diffractive rays makes use of fast beam tracing, whose core is two dimensional. In order to be able to model UTD in fast beam tracing, we need therefore to first flatten the 3D geometry onto a 2D environment and later to adapt the 2D diffractive rays to the 3D nature of UTD. In order to clamp down the 3D geometry to the floor map, we need to establish a correspondence between the 3D geometric primitives that contribute to the Uniform Theory of Diffraction and some 2D geometric primitives. For example, when projected on a floor map, an infinitely long diffracting edge becomes a diffractive point, and a 3D diffracted ray becomes a 2D diffracted ray. When tracing diffractive beams, each wedge illuminated (directly or indirectly) by the source will originate a disk of diffracted rays, as shown in Figure 8. At this point we need to consider the 3D nature of the environment. We do so by "lifting" the diffracted rays in the vertical direction. We will end up with sort of an extruded cylinder containing all the rays that are diffracted by the edge. However, when we specify the locations of the source and the receiver, we find that this set includes also paths that do not honor the Keller cone condition
), the conic surface flattens onto a disc. This particular situation would be of special interest to us if we were considering an inherently 2D geometry. This, however, is NOT our case. We are, in fact, considering the situation of "separable" 3D environments [12], which result from the cartesian product between a 2D environment (floor map) and a 1D (vertical) direction. This special geometry (sort of an extruded floor map) requires the modeling of diffraction and diffusion phenomena in a 3D space. The Uniform Theory of Diffraction is, in fact, inherently three-dimensional, but our approach to the tracing of diffractive rays makes use of fast beam tracing, whose core is two dimensional. In order to be able to model UTD in fast beam tracing, we need therefore to first flatten the 3D geometry onto a 2D environment and later to adapt the 2D diffractive rays to the 3D nature of UTD. In order to clamp down the 3D geometry to the floor map, we need to establish a correspondence between the 3D geometric primitives that contribute to the Uniform Theory of Diffraction and some 2D geometric primitives. For example, when projected on a floor map, an infinitely long diffracting edge becomes a diffractive point, and a 3D diffracted ray becomes a 2D diffracted ray. When tracing diffractive beams, each wedge illuminated (directly or indirectly) by the source will originate a disk of diffracted rays, as shown in Figure 8. At this point we need to consider the 3D nature of the environment. We do so by "lifting" the diffracted rays in the vertical direction. We will end up with sort of an extruded cylinder containing all the rays that are diffracted by the edge. However, when we specify the locations of the source and the receiver, we find that this set includes also paths that do not honor the Keller cone condition  , and are therefore to be considered as unfeasible. The removal of all unfeasible diffracted rays can be done during the auralization phase. During the auralization, in fact, we select the paths coming from the closer diffractive wedges, as they are considered to be more perceptually relevant. The validation is a costly iterative process, therefore we only apply it to paths that are likely to be kept during the auralization.
, and are therefore to be considered as unfeasible. The removal of all unfeasible diffracted rays can be done during the auralization phase. During the auralization, in fact, we select the paths coming from the closer diffractive wedges, as they are considered to be more perceptually relevant. The validation is a costly iterative process, therefore we only apply it to paths that are likely to be kept during the auralization.
3.3. New Needs and Requirements
As already said above, we are interested in extending the use of visibility maps for an accurate modeling and a fast rendering of diffusion and diffraction phenomena. As visibility diagrams were conceived for modeling specular reflections, it is important to discuss what needs and requirements need to be considered.
Diffraction
Visibility regions can be used for accommodating and modeling diffraction phenomena. In fact, according to the UTD, when illuminated by a beam, a diffractive edge becomes a virtual source with specific characteristics. Our goal is to model the indirect illumination of the receiver by means of secondary paths: wavefronts are emitted from the source, after an arbitrary number of reflections they fall onto the diffractive edge, which in turn illuminates the receiver after an arbitrary number of reflections. A common simplification that is adopted in works that deal with this phenomenon [14] consists of assuming that second and higher-order diffractions are of negligible impact onto the auralization result. This, in fact, is a perceptually reasonable choice that considerably reduces the complexity of the problem. In fact, a simple solution for implementing the phenomenon using the tracing tools at hand, consists of deriving a specialized beam-tree for each diffractive source. We will see later how. Another important aspect to consider in the modeling of diffraction is the Keller-cone condition [31], as briefly motivated above: with reference to Figure 8 we have to retain paths for which  . Tsingos et al. in [14] proposed to account for it by generating a reduced beam-tree, as constrained by a generalized cone that conservatively includes the Keller-cone. The excess rays that do not belong to the Keller cone, are removed afterwards through an appropriate check. We will see later that this approach can be implemented using the visibility diagrams.
. Tsingos et al. in [14] proposed to account for it by generating a reduced beam-tree, as constrained by a generalized cone that conservatively includes the Keller-cone. The excess rays that do not belong to the Keller cone, are removed afterwards through an appropriate check. We will see later that this approach can be implemented using the visibility diagrams.
Diffusion
Let us consider a source and a receiver, both facing a diffusive surface. In this case, each point of the surface generates an acoustic path between source and receiver. This means that the set of rays that emerge from the diffusing surface no longer form a beam (i.e., no virtual source can be defined as they do not meet in a specific point in space). In fact, according to Huygens principle, all points of the diffusive surface can be seen as secondary sources on a generally irregular surface, therefore we no longer have a single virtual source. Unlike diffraction, diffusion indeed poses new problems and challenges, as it prevents us from directly extending the beam tracing method in a straightforward fashion. One major difference from the specular case is the fact that the interaction between multiple diffusive surfaces cannot be described through an approach based on tracing, as we would have to face the presence of closed-loop diffusive paths. On the other hand, the impact of a diffusive surface on the acoustic field intensity is rather strong, therefore we cannot expect an acoustic path to still be of some significance after undergoing two or more diffusive reflections. It is thus quite reasonable to assume that any relevant acoustic paths would not include more than one relevant diffusive reflection along its way. We will see later on that this assumption, reasonably adopted by other authors as well (see [13]) opens the way to a viable solution to the real-time rendering of such acoustic phenomena. In fact, even if a diffusive surface does not preserve beam-like geometries, it is still possible to work on the visibility regions to speed up the tracing process between a source and a receiver through a diffusive reflection. This can be readily generalized to the case in which a chain of rays go from a source through a series of specular reflections and finally undergoes a diffusive reflection before reaching the receiver (diffusive path between a virtual source and a real receiver). A further generalization will be given for the case in which the rays undergo all specular reflections but one, which could be a diffusive reflection somewhere in between the chain. This last case corresponds to one diffusive path between a virtual source and a "virtual receiver", which can be computed by means of two intersecting beam-trees (a forward one from the source to the diffusive reflector and a backward one from the receiver to the diffusive reflector).
4. Tracing Diffusive Paths Using Visibility Diagrams
As already said before, the rendering of diffusion phenomena is commonly based on Bidirectional Beam Tracing, from both the source and the receiver. The need of tracing beams not just from the source but also from the receiver requires a certain degree of symmetrization in the definitions. For example, we need to introduce the concept of "virtual receiver", which is the location of the receiver as it gets iteratively mirrored against reflectors.
Let us consider the situation shown in Figure 9: a (virtual) source  and a (virtual) receiver
and a (virtual) receiver  face the diffusive reflector
face the diffusive reflector  . Reflector
. Reflector  partially occludes
partially occludes  with respect to
with respect to  . In order to simplify the problem we singled out the diffusive path
. In order to simplify the problem we singled out the diffusive path  . Figure 9 also shows the image-source
. Figure 9 also shows the image-source  , obtained by mirroring
, obtained by mirroring  over (the prolongation of)
over (the prolongation of)  . Notice that the geometry (lengths and angles) of the path
. Notice that the geometry (lengths and angles) of the path  is preserved if we consider the path
is preserved if we consider the path  . We can therefore consider the virtual source
. We can therefore consider the virtual source  instead of
instead of  , and trace the diffuse paths onto the visibility diagram "from" the reference diffusing reflector. If the coordinates of
, and trace the diffuse paths onto the visibility diagram "from" the reference diffusing reflector. If the coordinates of  and
and  in the normalized geometric domain are
in the normalized geometric domain are  and
and  , respectively, then the set of diffuse rays can be represented by
, respectively, then the set of diffuse rays can be represented by

In other words, we are searching for the directions  and
and  of the rays that originate from the point
of the rays that originate from the point  on the reference reflector and pass through
on the reference reflector and pass through  and
and  .
.
The diffuse paths can be quite easily represented in the RRP from the reference reflector. The path from a point  on the reflector is, in fact, the intersection of the dual of
on the reflector is, in fact, the intersection of the dual of  , which is the line
, which is the line  ; with the dual of
; with the dual of  , which is the line
, which is the line  . Similarly, the ray from
. Similarly, the ray from  to
to  is the intersection between the line
is the intersection between the line  and the line
and the line  . As we can see, we do not just have the ray that corresponds to the intersection of the two lines
. As we can see, we do not just have the ray that corresponds to the intersection of the two lines  and
and  (same point, same direction), but a whole collection of rays corresponding to the horizontal segment that connects the source line
(same point, same direction), but a whole collection of rays corresponding to the horizontal segment that connects the source line  and the receiver line
and the receiver line  (same point but different directions).
(same point but different directions).
Notice, however, that we have not yet considered potential occlusions of the diffuse paths from other reflectors in the environment. In Figure 9 we can see that only a portion of  contributes to diffusion. In fact there is a portion of
contributes to diffusion. In fact there is a portion of  that is not visible from
that is not visible from  , as it is occluded by
, as it is occluded by  . This occlusion can be easily identified in the dual space by following a similar reasoning to that of (2) for the tracing of specular reflective paths. The set of rays that are potentially occluded by
. This occlusion can be easily identified in the dual space by following a similar reasoning to that of (2) for the tracing of specular reflective paths. The set of rays that are potentially occluded by  is represented in the dual space by the beam obtained by intersecting
is represented in the dual space by the beam obtained by intersecting  with the visibility region of
with the visibility region of  . In order to test whether the beam is actually occluded by
. In order to test whether the beam is actually occluded by  or not, we can simply pick any ray within that area and check whether it reaches
or not, we can simply pick any ray within that area and check whether it reaches  before
before  . The dual space representation of the problem of Figure 9 is described in the right-hand side of Figure 10 (the geometric description of the same problem is shown on the left-hand side of the same Figure, for reasons of convenience). In the example of Figure 10 the line of sight between
. The dual space representation of the problem of Figure 9 is described in the right-hand side of Figure 10 (the geometric description of the same problem is shown on the left-hand side of the same Figure, for reasons of convenience). In the example of Figure 10 the line of sight between  and
and  is partially occluded by
is partially occluded by  , therefore only the segment
, therefore only the segment  contributes to diffusive paths. Let us consider, for example, the path
contributes to diffusive paths. Let us consider, for example, the path  , which is the line
, which is the line  . The directions of the rays from
. The directions of the rays from  to
to  and
and  are given by
are given by  and
and  , respectively. Notice that until now, for reasons of simplicity, we have considered
, respectively. Notice that until now, for reasons of simplicity, we have considered  to be the receiver, which forces the diffusion to occur last along the acoustic path. In order to make the proposed approach equivalent to bidirectional beam tracing, we will consider that
to be the receiver, which forces the diffusion to occur last along the acoustic path. In order to make the proposed approach equivalent to bidirectional beam tracing, we will consider that  is the receiver or a virtual receiver obtained by building a beam-tree from the receiver location. In order to contain the computational cost, we only consider low-order virtual sources and virtual receivers. In Section 7, for example, we limit the order of virtual sources and virtual receivers to three.
is the receiver or a virtual receiver obtained by building a beam-tree from the receiver location. In order to contain the computational cost, we only consider low-order virtual sources and virtual receivers. In Section 7, for example, we limit the order of virtual sources and virtual receivers to three.
5. Tracing Diffractive Beams and Paths Using Visibility Diagrams
In this section we extend the use of visibility diagrams to model diffractive paths and, using the UTD, we generalize the fast beam tracing method of [12] to account for this propagation phenomenon.
5.1. Selection of the Diffractive Wedges
As already discussed in [14], the diffractive field turns out to be less relevant when source and receiver are in direct visibility. The very first step of the algorithm consists, therefore, of selecting which edges are likely to generate a perceptually relevant diffraction. In what follows, we will refer to a wedge as a geometric configuration of two or more walls meeting into a single edge. If the angular opening of the wedge is smaller than  and both the receiver and the source fall inside the wedge, then source and receiver are in direct visibility. Not all wedges are, therefore, worth retaining. Even if a wedge is diffractive, we can still find configurations where source and receiver are in direct visibility. When this happens, diffraction is less relevant than the direct path and we discard these diffractive paths. With reference to Figure 11, we are interested in auralizing diffraction in the two regions marked as I and II, where source and receiver are not necessarily in conditions of mutual visibility. For each of the two regions we will build a beam-tree. This selection process returns a list
and both the receiver and the source fall inside the wedge, then source and receiver are in direct visibility. Not all wedges are, therefore, worth retaining. Even if a wedge is diffractive, we can still find configurations where source and receiver are in direct visibility. When this happens, diffraction is less relevant than the direct path and we discard these diffractive paths. With reference to Figure 11, we are interested in auralizing diffraction in the two regions marked as I and II, where source and receiver are not necessarily in conditions of mutual visibility. For each of the two regions we will build a beam-tree. This selection process returns a list  of diffractive wedges and their coordinates.
of diffractive wedges and their coordinates.
5.2. Tracing Diffractive Beam-Trees
With reference to Figure 12, our goal is to split the bundle of rays departing from the virtual source and directed towards the regions I and II into subbeams. In order to do this, we take advantage of the visibility diagrams. As seen in Section 3, the virtual source is placed on the tip of the diffracting wedge. The dual of this virtual source is the semi-infinite line of equation  or
or  , the sign depending on the normalization of the RRP. We are interested in auralizing the diffracted field only in regions I and II, therefore we evaluate the regional visibility along the lines (virtual sources in the geometric space)
, the sign depending on the normalization of the RRP. We are interested in auralizing the diffracted field only in regions I and II, therefore we evaluate the regional visibility along the lines (virtual sources in the geometric space)  only for
only for  or
or  . By scanning these semi-infinite lines along the visibility diagrams we can immediately determine all the visible reflectors of the above beams, and therefore determine their branching. Figure 12 shows the first-level beams and their dual representations for the configuration of Figure 11 (which refers to regions I and II). The propagation and the branching of these diffractive beams will follow the usual rules, according to the iterative tracing mechanism defined in Section 2 for specular reflections. The number of levels (branching order) of the diffractive beam-trees is indeed to be specified in a different fashion compared with reflective beam-trees, for reasons of relevance and computational load. We notice that, at this stage, the location of source or receiver does not need to be specified. As a consequence, we can build diffractive beam-trees in a precomputation phase.
. By scanning these semi-infinite lines along the visibility diagrams we can immediately determine all the visible reflectors of the above beams, and therefore determine their branching. Figure 12 shows the first-level beams and their dual representations for the configuration of Figure 11 (which refers to regions I and II). The propagation and the branching of these diffractive beams will follow the usual rules, according to the iterative tracing mechanism defined in Section 2 for specular reflections. The number of levels (branching order) of the diffractive beam-trees is indeed to be specified in a different fashion compared with reflective beam-trees, for reasons of relevance and computational load. We notice that, at this stage, the location of source or receiver does not need to be specified. As a consequence, we can build diffractive beam-trees in a precomputation phase.
5.3. Diffractive Paths Computation
Once source and receiver are specified, we can finally build the diffractive paths. Let  (
( ) denote the
) denote the  th reflective path between the source and the beam-tree to the region I (to the region II) departing from the diffractive wedge marked with
th reflective path between the source and the beam-tree to the region I (to the region II) departing from the diffractive wedge marked with  in the environment. As far as the auralization of diffraction is concerned, the path
in the environment. As far as the auralization of diffraction is concerned, the path  is completely defined if we specify the source location, the position of the point of incidence of the ray on the walls (possibly in normalized coordinates) and the location of the diffractive edge. The set of paths between the source and the diffractive region inside the beam-tree of the region I (II) is
is completely defined if we specify the source location, the position of the point of incidence of the ray on the walls (possibly in normalized coordinates) and the location of the diffractive edge. The set of paths between the source and the diffractive region inside the beam-tree of the region I (II) is  (
( ). Similarly,
). Similarly,  (
( ) is the
) is the  th path between the receiver and the
th path between the receiver and the  th diffractive wedge in the beam-tree I (II), and
th diffractive wedge in the beam-tree I (II), and  (
( ) is the set of paths between receiver and the diffractive edge inside the region I (II).
) is the set of paths between receiver and the diffractive edge inside the region I (II).
We are interested in diffractive paths where source and receiver fall in opposite regions: if the source falls within the beam-tree I, then we will check whether the receiver is in the beam-tree II, as diffraction is negligible when both source and receiver are in the same region. Let  be the set of paths associated to the diffractive edge
be the set of paths associated to the diffractive edge  (when the source is in beam-tree I, and the receiver in II). Similarly,
(when the source is in beam-tree I, and the receiver in II). Similarly,  is the set of paths where the source is in the beam-tree II and the receiver is in I. These sets are obtained as
is the set of paths where the source is in the beam-tree II and the receiver is in I. These sets are obtained as

where  denotes the cartesian product. Finally, the set of paths for the diffractive edge
denotes the cartesian product. Finally, the set of paths for the diffractive edge  is the union of
is the union of  and
and  :
:

In order to preserve the Keller cone condition, we have to determine the point  on the diffractive edge that makes the angle
on the diffractive edge that makes the angle  between the incoming ray and the edge equal to the angular aperture of the Keller cone
between the incoming ray and the edge equal to the angular aperture of the Keller cone  . When dealing with diffractive beam-trees which include also one or more reflections, the condition
. When dealing with diffractive beam-trees which include also one or more reflections, the condition  is no longer sufficient for determining the location of the virtual source, as we must also preserve the Snell's law for the reflections inside the path. In [14] the authors propose to compute the diffraction and reflection points along the diffractive path through a system of nonlinear equations. This solution is obtained through an iterative Newton-Raphson algorithm. In this paper we adopt the same approach.
is no longer sufficient for determining the location of the virtual source, as we must also preserve the Snell's law for the reflections inside the path. In [14] the authors propose to compute the diffraction and reflection points along the diffractive path through a system of nonlinear equations. This solution is obtained through an iterative Newton-Raphson algorithm. In this paper we adopt the same approach.
6. Applications to Rendering
In this section we discuss the above beam tracing approach in the context of acoustic rendering. As anticipated, we first discuss the more traditional case of channel-based (point-to-point) rendering. This is the case of auralization when the user is wearing a headset.
We will then discuss the case of geometric wavefield rendering.
6.1. Path-Tracing for Channel Rendering
In this section we propose and describe a simple auralization system based on the solutions proposed above. Due to their different nature, we will distinguish between reflective, diffusive and diffractive echoes. In particular, diffraction involves a perceptually relevant low-pass filtering on the signal, hence we will stress diffraction instead of diffusion and reflection. The diffraction is rendered by a coefficient, whose value depends on the frequency. Each diffractive wedge, therefore, acts like a filter on the incoming signal, with an apparent impact on the overall computational cost. We therefore made our auralization algorithms select the most significant paths only, based on a set of heuristic rules that take the power of each diffractive filter into account.
6.1.1. Auralization of Reflective Paths
As far as reflections are concerned, we follow the approach proposed in [12]: the echo  is characterized by a length
is characterized by a length  . The magnitude of the
. The magnitude of the  th echo is
th echo is  ,
,  being the reflection coefficient and
being the reflection coefficient and  being the number of reflections (easily determined by inspecting the beam-tree). The delay associated to the echo
being the number of reflections (easily determined by inspecting the beam-tree). The delay associated to the echo  is
is  , where
, where  is the speed of sound (
is the speed of sound ( m/s in our experiments).
m/s in our experiments).
6.1.2. Auralization of Diffraction
As motivated in Section 5, we have resorted to UTD to render diffraction. In order to auralize diffraction paths, we have to compute a diffraction coefficient, which exhibits a frequency-dependent behavior. A comprehensive tutorial on the computation of the diffraction coefficient in UTD may be found in [14]. We remark here that in order to compute the diffractive filter, for each path we need some geometrical information about the wedge (available at a precomputation stage) and about the path, which is available only after the Newton Raphson algorithm described in the previous Section.
6.1.3. Auralization of Diffusive Paths
Accurate modeling of diffusion is typically based on statistical methods [33]. Our modeling solution is, in fact, aimed at auralization and rendering applications, therefore we resort to an approximated but still reliable approach that does not significantly impact on the computational cost: we make use of the Lambert cosine law, which works for energies, to compute the energy response. Then we convert the energy response onto a pressure response by taking its square root. A similar idea was developed in [34], where the author combines beam tracing and radiosity.
In order to compute the energy response, we need the knowledge of the position of the virtual source and receiver and the segment on the illuminating reflector from which rays depart. The energy response  of the diffusive path from reflector
of the diffusive path from reflector  is given by the integration of the contributions of each point of the reflector. If the length of the diffusive portion is
is given by the integration of the contributions of each point of the reflector. If the length of the diffusive portion is  , then the auralization filter may be approximated as
, then the auralization filter may be approximated as

where  is the coordinate on the diffuser,
is the coordinate on the diffuser,  is the number of portions in which the segment has been subdivided and
is the number of portions in which the segment has been subdivided and  is modeled according to the Lambert cosine law:
is modeled according to the Lambert cosine law:

and  and
and  are the directions of the incident and outgoing rays referred to the axis of the reflector, respectively. Angles
are the directions of the incident and outgoing rays referred to the axis of the reflector, respectively. Angles  and
and  are related to
are related to  and
and  according to
according to

6.2. Beam Tracing for Sound Field Rendering
The beam-tree contains all the information that we need to structure a sound field as a superposition of individual beams, each originating from a different image-source. A solution was recently proposed for reconstructing an individual beam in a parametric fashion using a loudspeaker array [16]. Here, an arbitrary beam of prescribed aperture, orientation origin is reconstructed using an array of loudspeakers. In particular, the least squares difference of the wavefields produced by the array of loudspeakers and by the virtual source is minimized over a set of predefined control points. The minimization returns a spatial filter to be applied at each loudspeaker. It is interesting to notice that the approach described in [16] offers the possibility to design a spatial filter that performs a nonuniform weighting of the rays within the same beam. This feature enables the rendering of "tapered" beams, which is particularly useful when dealing with diffractive beams. In fact, the diffraction coefficient (see [14] for further details) assigns different levels of energy to rays within the same beam, according to the reciprocal geometric configuration of the source, the wedge and the direction of travel of the ray departing from the wedge.
The rendering of the overall sound field is finally achieved by adding together the spatial filters for the individual beams. More details and a some preliminary results of this method can be found in [35].
7. Experimental Results
In order to test the validity of our solution, we performed a series of simulation experiments as well as a measurement campaign in a real environment. An initial set of simulations was performed with the goal of assessing the computational efficiency of our techniques for the auralization of reflective, diffractive and diffusive paths, separately considered. In order to assess the accuracy of our method, were constructed the impulse responses of a given environment (on an assigned grid of points) through both simulation and direct measurements. From such impulse responses, we derived a set of parameters, typically used for describing reverberation. The comparison between the measured parameters and the simulated ones was aimed at assessing the extent of the improvement brought by introducing cumulatively diffraction and diffusion into our simulation.
7.1. Computation Time
In order to assess the computational efficiency of the proposed method, we conducted a series of simulations in environments of controlled complexity (variable geometry). We developed a procedure for generating testing environments with an arbitrary number of  rooms, all chained together as shown in Figure 13. An
rooms, all chained together as shown in Figure 13. An  -room environment is therefore made of
-room environment is therefore made of  reflectors. In order to enable acoustic interaction between rooms, each one of the intermediate walls exhibits a randomly-placed opening. In our tests, we generated environments with 20, 40, 80, 120, 320, 640 such walls. The simulation platform was based on an Intel Mobile Pentium processor equipped with 1 GB of RAM, and the goal was to:
reflectors. In order to enable acoustic interaction between rooms, each one of the intermediate walls exhibits a randomly-placed opening. In our tests, we generated environments with 20, 40, 80, 120, 320, 640 such walls. The simulation platform was based on an Intel Mobile Pentium processor equipped with 1 GB of RAM, and the goal was to:
-
(i)
compare the beam-tree's building time of visibility-based beam tracing with that of traditional beam tracing [5];
-
(ii)
measure the diffractive path-tracing time;
-
(iii)
measure the diffusive path-tracing time.
As far as the time spent by the system in computing the visibility diagrams is concerned, we invite the reader to [12]. The beam-tree building time is intended as the time spent by the algorithm in tracing a preassigned number of beams. In order to assess the impact of the proposed approach on this specific parameter, in comparison with a traditional beam-tracing approach, we stopped the algorithm when 10,000 beams were traced. The simulation results are shown in Figure 14. As expected, our approach turns out to outperform traditional beam tracing. As the beam-tree building time strongly depends on the source location, we conducted numerous tests by placing the source at the center of each one of the rooms of the modular environments. The beam-tree building time was then computed as the average of the beam-tree building times over all such simulations. In order to test the tracing time of the diffusive paths the source has been placed in the center the modular environment. We conducted several experiments placing the receiver at the center of each one of the rooms. We measured the time spent by the system in computing the diffusive paths. We considered up to three reflections before and after the diffuse interaction. Figure 15 shows the average tracing time of the diffusive paths as a function of the number of walls. If we are interested in an accurate rendering, we should trace at least 1000 beams: in this situation we notice that even in a complex environment (e.g., 640 walls) the auralization of the diffusive paths takes only a fraction of the time spent by the system for the auralization of the reflective paths. The last test is aimed at assessing the computational time for auralizing the diffractive paths. As done above, the source was placed at the center of the environment and we conducted several experiments, placing the receiver at the center of each room. In particular in this situation two tests have been conducted:
-
(i)
the number of diffractive paths with respect to the number of walls in the environment;
-
(ii)
the computational time for auralizing the diffractive paths.
Tracing time of the diffusive paths as a function of the number of walls of the environment of Figure 13.
Figure 16 shows the time that the system takes to auralize the diffractive paths, as a function of the number of walls in the environment. Figure 17 shows the number of paths for the same experiment. The number of diffractive paths depends upon both the depth of the diffractive beam-trees and the number of diffractive edges in the environment in quite an unpredictable fashion. Notice that the auralization for the diffractive paths can exceed the auralization of the reflective paths. However, we should keep in mind that the computation of over 1000 diffractive paths can be quite redundant from a perceptual standpoint. We propose here to select the diffractive paths arisen from the closer diffractive wedges, as they are more perceptually relevant.
7.2. Validation
It becomes important to assess how well spatial distributions of reverberations are rendered by this approach. In order to do so, we conducted comparative tests between simulated data and real data with corresponding geometries. We placed a high-quality loudspeaker in a reverberant environment and used it to reproduce a MLS sequence [36]. The environment's floor map is shown in Figure 18, where the location of the loudspeaker and microphone are marked with green and red dots, respectively. The acquired signals were then processed to determine the impulse responses of the environment in those locations, as described in [36]. The reflective and diffusive reflection coefficients of the walls, indeed, could not be directly measured but were coarsely determined so that the  of the simulated impulse response would approximate the estimated one in a given test position. As a sample-to-sample comparison of the acquired and simulated impulse responses is not very informative, we compared some parameters that describe the impulse response, which can be readily derived from the simulated and measured impulse responses. In particular, we run extensive simulations first with reflections only (up to the 16th order of the beam-tree), with diffraction (up to the 6th order) and finally with diffusion (with an order 3).
of the simulated impulse response would approximate the estimated one in a given test position. As a sample-to-sample comparison of the acquired and simulated impulse responses is not very informative, we compared some parameters that describe the impulse response, which can be readily derived from the simulated and measured impulse responses. In particular, we run extensive simulations first with reflections only (up to the 16th order of the beam-tree), with diffraction (up to the 6th order) and finally with diffusion (with an order 3).
Early Decay Time (EDT)
EDT is the time that the Schroeder envelope of the impulse response takes to drop of 10 dB. A comparison of the EDT maps (geographical distribution of the EDT in the measured and simulated cases) is shown in Figure 19. Notice that the impact of diffusion in this experiment is quite significant: in fact, as expected, including diffusion increases the energy in the "tail" of the impulse response, with the result of obtaining a more realistic reverberation.
Normalized Energy of the Impulse Response
where the normalization is performed with respect to the impulse response of maximum energy. A comparison between normalized energy maps is shown in Figure 20. Once again we notice that a simulation of all phenomena (reflections, diffraction and diffusion) produces more realistic results.
Center Time
It is first-order momentum of the squared impulse response. The Center Time (CT) map is shown in Figure 21, where we see that a simulation based on reflections, diffraction and diffusion allows us to achieve, once again, a good match. We notice, in particular, that modeling diffusion increases the level of smoothness of the simulated map, which makes it more similar to the measured one.
8. Conclusions
In this paper we proposed an extension of the visibility-based beam tracing method proposed in [12], which now allows us to model and render propagation phenomena such as diffraction and diffusion, without significantly affecting the computational efficiency. We also improved the method in [12] by showing that not just the construction of the beam-tree but also the whole path-tracing process can be entirely performed on the visibility maps. We finally showed that this approach produces quite accurate results when comparing simulated data with real acquisitions. Thanks to that, this modeling tool proves particularly useful every time there is a need for an accurate and fast simulation of acoustic propagation in environments of variable geometry and variable physical characteristics.
References
Kopuz S, Lalor N: Analysis of interior acoustic fields using the finite element method and the boundary element method. Applied Acoustics 1995, 45(3):193-210. 10.1016/0003-682X(94)00045-W
Kludszuweit A: Time iterative boundary element method (TIBEM)—a new numerical method of four-dimensional system analysis for thecalculation of the spatial impulse response. Acustica 1991, 75: 17-27.
Ciskowski R, Brebbia C: Boundary Element Methods in Acoustics. Elsevier, Amsterdam, The Netherlands; 1991.
Krockstadt U: Calculating the acoustical room response by the use ofa ray tracing technique. Journal of Sound and Vibrations 1968, 8(1):118-125. 10.1016/0022-460X(68)90198-3
Heckbert PaulS, Hanrahan : Beam tracing polygonal objects. Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, July 1984 119-127.
Dadoun N, Kirkpatrick D, Walsh J: The geometry of beam tracing. Proceedings of the ACM Symposium on Computational Geometry, June 1985, Sedona, Ariz, USA 55-61.
Monks M, Oh B, Dorsey J: Acoustic simulation and visualisationusing a new unified beam tracing and image source approach. Proceedings of the 100th Audio Engineering Society Convention (AES '96), 1996, Los Angeles, Ariz, USA
Stephenson U, Kristiansen U: Pyramidal beam tracing and time dependent radiosity. Proceedings of the 15th International Congress on Acoustics, June 1995, Trondheim, Norway 657-660.
Walsh JP, Dadoun N: What are we waiting for? The developmentof Godot, II. Journal of the Acoustical Society of America 1982, 71(S1):S5.
Funkhouser T, Carlbom I, Elko G, Pingali G, Sondhi M, West J: Beam tracing approach to acoustic modeling for interactive virtual environments. Proceedings of the Annual Conference on Computer Graphics (SIGGRAPH '98), July 1998 21-32.
Laine S, Siltanen S, Lokki T, Savioja L: Accelerated beam tracing algorithm. Applied Acoustics 2009, 70(1):172-181. 10.1016/j.apacoust.2007.11.011
Antonacci F, Foco M, Sarti A, Tubaro S: Fast tracing of acoustic beams and paths through visibility lookup. IEEE Transactions on Audio, Speech and Language Processing 2008, 16(4):812-824.
Funkhouser T, Min P, Carlbom I: Real-time acoustic modeling for distributed virtual environments. In Proceedings of ACM Computer Graphics (SIGGRAPH '99), 1999, Los Angeles, Ariz, USA Edited by: Rockwood A. 365-374.
Tsingos N, Funkhouser T, Ngan A, Carlbom I: Modeling acoustics in virtual environments using the uniform theory of diffraction. Proceedings of the 28th International Conference on Computer Graphics and Interactive Techniques (SIGGRAPH 2001), August 2001 545-552.
Kouyoumjian RG, Pathak PH: A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface. Proceedings of the IEEE 1974, 62(11):1448-1461.
Canclini A, Galbiati A, Calatroni A, Antonacci F, Sarti A, Tubaro S: Rendering of an acoustic beam through an array of loud-speakers. Proceedings of the 12th International Conference on Digital Audio Effects (DAFx '09), 2009
Berkhout AJ: Holographic approach to acoustic control. Journal of the Audio Engineering Society 1988, 36(12):977-995.
Foco M, Polotti P, Sarti A, Tubaro S: Sound spatialization basedon fast beam tracing in the dual space. Proceedings of the 6th International Conference on Digital Audio Effects (DAFX '03), September 2003, London, UK 198-202.
Brouard B, Lafarge D, Allard J-F, Tamura M: Measurement and prediction of the reflection coefficient of porous layers at oblique incidence and for inhomogeneous waves. Journal of the Acoustical Society of America 1996, 99(1):100-107. 10.1121/1.415222
Kleiner M, Gustafsson H, Backman J: Measurement of directional scattering coefficients using near-field acoustic holography and spatial transformation of sound fields. Journal of the Audio Engineering Society 1997, 45(5):331-346.
Nocke C: In-situ acoustic impedance measurement using a free-field transfer function method. Applied Acoustics 2000, 59(3):253-264. 10.1016/S0003-682X(99)00004-3
Thomasson SI: Reflection of waves from a point source by an impedance boundary. Journal of the Acoustical Society of America 1976, 59(4):780-785. 10.1121/1.380943
Funkhouser T, Tsingos N, Jot JM: Sounds good to me! computational sound for graphics, virtual reality, and interactive systems. Proceedings of ACM Computer Graphics (SIGGRAPH '02), July 2002, San Antonio, Tex, USA
Kuttruff H: Room Acoustics. 3rd edition. Elsevier, Amsterdam, The Netherlands; 1991.
Beranek LL: Concert and Opera Halls: How they Sound. Acoustical Society of America through the American Institute of Physics; 1996.
Tsingos N: Simulating high quality virtual sound fields for interactive graphics applications, Ph.D. dissertation. Universite J. Fourier, Grenoble, France; 1998.
Biot MA, Tolstoy I: Formulation of wave propagation in infinite media by normal coordinates with an application to diffraction. Journal of the Acoustical Society of America 1957, 29: 381-391. 10.1121/1.1908899
Lokki T, Savioja L, Svensson P: An efficient auralization of edge diffraction. Proceedings of 21st International Conference of Audio Engineering Society (AES '02), May 2002
Svensson UP, Fred RI, Vanderkooy J: An analytic secondary source model of edge diffraction impulse responses. Journal of the Acoustical Society of America 1999, 106(5):2331-2344. 10.1121/1.428071
Torres RR, Svensson UP, Kleiner M: Computation of edge diffraction for more accurate room acoustics auralization. Journal of the Acoustical Society of America 2001, 109(2):600-610. 10.1121/1.1340647
Keller JB: Geometrical theory of diffraction. Journal of the Optical Society of America 1962, 52: 116-130. 10.1364/JOSA.52.000116
McNamara D, Pistorius C, Malherbe J: Introduction to the Uniform Geometrical Theory of Diffraction. Artech House; 1990.
Rindel JH: The use of computer modeling in room acoustics. Journal of Vibroengineering 2000, 3: 41-72.
Lewers T: A combined beam tracing and radiatn exchange computer model of room acoustics. Applied Acoustics 1993, 38(2–4):161-178.
Antonacci F, Calatroni A, Canclini A, Galbiati A, Sarti A, Tubaro S: Soundfield rendering with loudspeaker arrays through multiple beam shaping. Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA '09), 2009 313-316.
Rife DD, Vanderkooy J: Transfer-function measurement with maximum-length sequences. Journal of the Audio Engineering Society 1989, 37(6):419-444.
Acknowledgment
The research leading to these results has received funding from the European Community's Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 226007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Antonacci (EURASIP Member), F., Sarti (EURASIP Member), A. & Tubaro (EURASIP Member), S. Two-Dimensional Beam Tracing from Visibility Diagrams for Real-Time Acoustic Rendering. EURASIP J. Adv. Signal Process. 2010, 642316 (2010). https://doi.org/10.1155/2010/642316
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/642316


 and
and  . For some rays (e.g.,
. For some rays (e.g.,  )
)  )
) 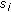 ,
,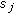 (if any),
(if any), in the normalized reference frame,
in the normalized reference frame,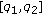 that identifies the "illuminating" region on the
that identifies the "illuminating" region on the 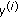 -axis,
-axis,






 . Reflector
. Reflector  is the image-source of Smirrored over the prolongation of
is the image-source of Smirrored over the prolongation of  and
and  form a diffusive path.
form a diffusive path.
 and
and  are the dual of the points
are the dual of the points  and R.
and R.


 rooms are all connected together through randomly-located apertures.
rooms are all connected together through randomly-located apertures.






