- Research Article
- Open access
- Published:
Wavefront Reconstruction of Elevation Circular Synthetic Aperture Radar Imagery Using a Cylindrical Green's Function
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 657323 (2009)
Abstract
Elevation Circular Synthetic Aperture Radar (E-CSAR) is a novel radar modality used to form radar images from data sets acquired along a complete or even a segment of a cylindrical geometry above a given scan area. Due to the nonlinear nature of the target signatures on the E-CSAR data sets, the collected data must be focused. In this paper, a novel E-CSAR reconstruction algorithm is proposed. The proposed method uses a new formulation of the Green's function of an E-CSAR scan geometry in which the phase components introduced by the scan geometry can be clearly identified and their effects can be effectively compensated. Additionally, theoretical aspects of the point spread function related to this new Green's function were determined. The feasibility of the proposed technique was assessed using experimental data sets. The proposed method yielded spatially accurate images and exhibited an average execution time in the order of minutes.
1. Introduction and Motivation
Since its origins in 1951, Synthetic Aperture Radar (SAR) has been used for a wide variety of applications, from military reconnaissance to agricultural imaging to only name two examples [1]. Similarly to other radar imaging modalities, SAR techniques collect the reflections from an irradiated area and process them to create a reflectivity map from the scattering bodies present in the imaged region [2]. The SAR data acquisition process can be described as follows. A trajectory over the scan region is defined. Along this trajectory, an illuminating source radiates an ultra-wideband waveform and records the collected reflections from the objects inside the scan area. The recorded reflections are then processed to eliminate the distortions caused by the antenna, the shape of the irradiated waveform, and the motion of the moving platform [3–5]. Finally, the resulting reflectivity map can be visualized and interpreted.
The most commonly used scan geometries in SAR imaging scenarios are linear trajectories [3]. However, this kind of scan geometries only offer a limited view of the targets present in the scan region, which may difficult the interpretation and recognition of the different target signatures present in the image [6]. This is due to the fact that a target can present different signatures depending on its orientation with respect to the scan geometry. The amount of power reflected from a given target varies according to the dielectric contrast between the target and the propagation medium, the relative reflecting area of the target when viewed from the illuminating location, and the radiated power density [7]. For example, the power reflected from a sphere is the same when illuminated from any given location. On the other hand, the reflected power from a flat metal plate varies according to its orientation with respect to the illuminating beam. The signature variations may difficult the interpretation of the target locations and orientations in the resulting SAR images. This task becomes even more complicated if a 3D reflectivity map from the scan region is required. Nevertheless, this problem can be solved by spotlighting the scan region using a cylindrical scan geometry [8]. This SAR modality is called Elevation Circular Synthetic Aperture Radar (E-CSAR) [3].
Similarly to other SAR scan geometries, E-CSAR data sets must be focused in order to be properly visualized and interpreted. Several reconstruction approaches have been proposed for this SAR modality, including Time Domain Correlation (TDC) techniques and Plane Wave Approximation (PWA) methods. However, TDC techniques have execution times in the order of days or even weeks and PWA methods produce images with low focal quality, considerable spatial location errors and target smearing [9, 10]. An alternative approach is the use of waveform reconstruction techniques. These methods are based on performing a series of operations in the frequency domain that transfer the collected data from the spatiotemporal domain in which it was originally collected to the spatial domain where it will be displayed. It has been shown that wavefront reconstruction techniques produce spatially accurate E-CSAR images [3].
Nevertheless, current E-CSAR wavefront reconstruction approaches still present limitations such as the execution times in the order of hours and altitude constraints [8, 11]. These considerations limit the widespread use of E-CSAR techniques in scenarios where the geometry of the scan region or target detection requirements suit the E-CSAR advantages, such as novel near field applications like breast microwave imaging [12], wood inspection [13], and low altitude SAR imaging scenarios [14]. In this paper, a novel E-CSAR wavefront reconstruction algorithm is proposed. Unlike current E-CSAR wavefront reconstruction approaches, the proposed method uses a novel formulation of Green's function of the E-CSAR scan geometry that does not include a Hankel function and imposes no altitude restrictions on the inversion algorithm. The algorithm presented in this paper is an extension of the work presented by the authors in [15] for radar data sets acquired along cylindrical scan geometries. This paper is organized as follows. The E-CSAR signal model is explained in Section 2. In Section 3, the spectrum of Green's function corresponding to the E-CSAR scan geometry is calculated. The proposed reconstruction method is described in Section 4. A theoretical analysis of the point spread function of the E-CSAR imaging geometry, including aspects such as the spatial sampling constraints and resolution, is done in Section 4. In Section 5, the feasibility of the proposed method is assessed using experimental data sets. Lastly, some concluding remarks are mentioned in Section 6.
2. Signal Model
Consider the scan geometry depicted in Figure 1. In E-CSAR scan scenarios, the data acquisition process is performed along a series of circular trajectories in the ( ) plane defined along the
) plane defined along the  -axis. The antenna mainlobe is always pointing towards the center of a scan region with radius
-axis. The antenna mainlobe is always pointing towards the center of a scan region with radius  . The antenna radiation footprint is assumed to be constant over the scan region. A total of T targets are assumed to be present inside the scan area. The E-CSAR data acquisition process is performed as follows. At each scan location, a waveform
. The antenna radiation footprint is assumed to be constant over the scan region. A total of T targets are assumed to be present inside the scan area. The E-CSAR data acquisition process is performed as follows. At each scan location, a waveform  is irradiated and the responses from the targets present in the scan area are recorded. For the scan location at (
is irradiated and the responses from the targets present in the scan area are recorded. For the scan location at ( ), the received signal can be expressed as
), the received signal can be expressed as

where  denotes
denotes  ,
,  denotes
denotes  , and
, and  , c is the medium propagation speed,
, c is the medium propagation speed,  is the reflectivity of the p thtarget when irradiated from (
is the reflectivity of the p thtarget when irradiated from ( ,
,  , z), (
, z), ( ) is the location of the p th target, and
) is the location of the p th target, and  and
and  are the lower and upper spatial bounds of the scan trajectory along the azimuth direction. The frequency representation of the reflected signals from each target along the
are the lower and upper spatial bounds of the scan trajectory along the azimuth direction. The frequency representation of the reflected signals from each target along the  direction can be obtained by calculating its Fourier transform which yields the following expression:
direction can be obtained by calculating its Fourier transform which yields the following expression:

where  which is known as the wavenumber and
which is known as the wavenumber and  and
and  and
and  are the maximum and minimum frequency components of
are the maximum and minimum frequency components of  , and
, and  =
=  . The exponential term in (3) is also known as the spherical phase function of the imaging system [3].
. The exponential term in (3) is also known as the spherical phase function of the imaging system [3].
3. Wavefront Reconstruction
3.1. Green's Function Spectrum Calculation
The collected data sets are a function of the signal travel time and the recording spatial location. Due to the different travel times of the target reflections and the shape of the scan geometry, the target responses exhibit nonlinear signatures when viewed on the  domain. An example of this can be seen in Figure 2. This fact makes difficult to assess the locations and dimensions of the targets present in the scan area. If the collected data is directly mapped to a rectangular coordinate system, the target signatures appear at a shifted location and present a considerable augment on their dimensions. In order to properly visualize the target responses, the recorded data must be focused by transferring it from its original spatial temporal space to the spatial space related to the dimensions of the scan area. A common way of performing this process is to use the phase delay from the recorded reflections to determine its spatial location. This approach is known as wavefront reconstruction or holography [3, 16, 17].
domain. An example of this can be seen in Figure 2. This fact makes difficult to assess the locations and dimensions of the targets present in the scan area. If the collected data is directly mapped to a rectangular coordinate system, the target signatures appear at a shifted location and present a considerable augment on their dimensions. In order to properly visualize the target responses, the recorded data must be focused by transferring it from its original spatial temporal space to the spatial space related to the dimensions of the scan area. A common way of performing this process is to use the phase delay from the recorded reflections to determine its spatial location. This approach is known as wavefront reconstruction or holography [3, 16, 17].
Let define the following distance function:

where

The next step is to determine the Fourier transform of  in the angular and elevation domains. This operation is given by
in the angular and elevation domains. This operation is given by

where  , and
, and  are the spatial frequency counterparts of θ and
are the spatial frequency counterparts of θ and  respectively. To determine a closed form expression for (5), the stationary phase method will be used [17]. This technique determines the Asymptotic Behaviour (AB) of integrals containing a Phase Modulated (PM) function, as the value of the modulating terms tends to infinity. This approach determines the phase center of the PM term by analyzing the behaviour of its Instantaneous Frequency (IF). The AB is then determined by evaluating the PM function at the stationary point. The resulting expression is the frequency response of the imaging system. This technique has been used by several radar imaging reconstruction approaches to determine the frequency response of their corresponding imaging geometries [5, 18–21].
respectively. To determine a closed form expression for (5), the stationary phase method will be used [17]. This technique determines the Asymptotic Behaviour (AB) of integrals containing a Phase Modulated (PM) function, as the value of the modulating terms tends to infinity. This approach determines the phase center of the PM term by analyzing the behaviour of its Instantaneous Frequency (IF). The AB is then determined by evaluating the PM function at the stationary point. The resulting expression is the frequency response of the imaging system. This technique has been used by several radar imaging reconstruction approaches to determine the frequency response of their corresponding imaging geometries [5, 18–21].
To calculate the AB of (6), the first step determines the stationary points in each slow time trajectory,  and
and  . To make this process easier to follow, the value of
. To make this process easier to follow, the value of  will be calculated first. The IF in the
will be calculated first. The IF in the  direction is given by
direction is given by

The phase center along the  direction,
direction,  , is defined as follows:
, is defined as follows:

By making the left side of (6) equal to zero, the following expression is produced:

Notice how the left side of (8) resembles a trigonometric relationship. Taking advantage of this fact, (8) can be rewritten as

where  denotes
denotes  . By algebraically manipulating (9), the next expression is obtained:
. By algebraically manipulating (9), the next expression is obtained:

Next, the value of  will be used to determine the AB of (5) along the
will be used to determine the AB of (5) along the  direction. The resulting expression is
direction. The resulting expression is

where  is the spectrum amplitude component in the
is the spectrum amplitude component in the  domain,
domain,  and k
z
are the frequency counterparts of
and k
z
are the frequency counterparts of  and
and  , respectively, and
, respectively, and  =
=  . Next, the asymptotic behaviour in the
. Next, the asymptotic behaviour in the  direction will be calculated. The IF of the PM component of (11) in the
direction will be calculated. The IF of the PM component of (11) in the  direction is
direction is

The phase center  is defined as:
is defined as:

By algebraically manipulating (13), the following expression is obtained:

By using the fact that the left side of (14) resembles a sine law relationship, an analytical solution can be obtained. As depicted in Figure 3, a triangle between the p th target, the antenna, and the center of the scan pattern is formed. Using basic trigonometry concepts, it can be shown that  . Therefore, the relationship between
. Therefore, the relationship between  ,
,  and
and  is given by
is given by

From (16), the values of  and
and  are
are


Next, the AB of (5) is calculated by evaluating (11) at  . The resulting expression is
. The resulting expression is

where  is the spectrum amplitude component in the
is the spectrum amplitude component in the  frequency space. In the majority of the E-CSAR scenarios,
frequency space. In the majority of the E-CSAR scenarios,  (
( ) is defined over an
) is defined over an  discrete space (
discrete space ( ), where L is the number of time samples, N is the total scan locations in the circular scan pattern defined in the (
), where L is the number of time samples, N is the total scan locations in the circular scan pattern defined in the ( )-plane, M is the total number of scan planes along the
)-plane, M is the total number of scan planes along the  -axis, and l, n, and m denote the sample indexes along
-axis, and l, n, and m denote the sample indexes along  ,
,  , and
, and  scan trajectories in that order. Given that the Shannon-Nyquist theorem was satisfied the mathematical analysis shown in the last subsection holds true for the 3D discrete Fourier transform of
scan trajectories in that order. Given that the Shannon-Nyquist theorem was satisfied the mathematical analysis shown in the last subsection holds true for the 3D discrete Fourier transform of  (
( ), and
), and  , where
, where  ,
,  , and
, and  are the discrete counterparts of
are the discrete counterparts of  ,
,  , and
, and  , respectively.
, respectively.
3.2. Image Reconstruction
In order to properly visualize the recorded reflections, the effect of the scan geometry must be compensated and the data must the migrated from the ( ) domain to the rectangular space (
) domain to the rectangular space ( ) where it will be visualized and interpreted. The following steps can be used to form the 3D image,
) where it will be visualized and interpreted. The following steps can be used to form the 3D image,  , where a and b are the sample indexes along the
, where a and b are the sample indexes along the  - and y-axes, corresponding to the collected data set
- and y-axes, corresponding to the collected data set  (
( ).
).
( ) Calculate the 3D FFT of
) Calculate the 3D FFT of  (
( ). The result of this operation is
). The result of this operation is .
.
( ) Next, the effects of the scan trajectory on the collected data are removed. The phase terms in (18) can be divided into two main types. The first one, denoted by
) Next, the effects of the scan trajectory on the collected data are removed. The phase terms in (18) can be divided into two main types. The first one, denoted by , is the PM terms related to the target responses. These terms are a function of the target location, (
, is the PM terms related to the target responses. These terms are a function of the target location, ( ). The second type of spectral components,
). The second type of spectral components,  , is the PM terms related to the delays produced by the shape of the scan geometry. In order to eliminate the effects of the scan trajectory on the collected data,
, is the PM terms related to the delays produced by the shape of the scan geometry. In order to eliminate the effects of the scan trajectory on the collected data,  must be removed from
must be removed from  . This is achieved by performing the following operation:
. This is achieved by performing the following operation:

where  denotes the complex conjugate of
denotes the complex conjugate of  which is equal to
which is equal to

The resulting spectrum is given by

where  .
.
( ) The next step is to transfer the data in
) The next step is to transfer the data in  , from the
, from the  frequency space to the (
frequency space to the ( ) spatial frequency space, where
) spatial frequency space, where  and
and  are the spatial frequency counterparts of the x and y spatial domains. For this purpose, the auxiliary function
are the spatial frequency counterparts of the x and y spatial domains. For this purpose, the auxiliary function  will be used. Due to the fact that both
will be used. Due to the fact that both  and
and  are evenly sampled, the differences between adjacent values within
are evenly sampled, the differences between adjacent values within  vary across the grid in which the function is defined. As mentioned in [22], uneven sampled frequency spaces are unfit to be processed using FFT-based techniques. To generate a space without this issue, the function
vary across the grid in which the function is defined. As mentioned in [22], uneven sampled frequency spaces are unfit to be processed using FFT-based techniques. To generate a space without this issue, the function  is defined, where the differences between the values present at adjacent samples are the same for all its domain grid,
is defined, where the differences between the values present at adjacent samples are the same for all its domain grid,  . We will denote the set of values present in
. We will denote the set of values present in  by the (
by the ( ) frequency space. To produce a spectrum suitable to be processed using FFT techniques, the data present in each (
) frequency space. To produce a spectrum suitable to be processed using FFT techniques, the data present in each ( ) plane in
) plane in  , is interpolated into the frequency values specified in the (
, is interpolated into the frequency values specified in the ( ) space. This operation is performed for each plane in the
) space. This operation is performed for each plane in the  direction. The outcome of this process will be referred as
direction. The outcome of this process will be referred as  . This process is also known as Stolt`s interpolation [19–21].
. This process is also known as Stolt`s interpolation [19–21].
( ) The inverse FFT of the focused data is computed on the
) The inverse FFT of the focused data is computed on the  direction, resulting in a representation of the collected data in the (
direction, resulting in a representation of the collected data in the ( ) domain. We will refer to the resulting spectrum by
) domain. We will refer to the resulting spectrum by 
( ) At this point, a new frequency space, denoted by (
) At this point, a new frequency space, denoted by ( ) is generated, where
) is generated, where

This mapping is performed for the ( ) plane corresponding to each
) plane corresponding to each  value.
value.
( ) Next, we can map
) Next, we can map  into
into  using the following function:
using the following function:

where the corresponding  for each
for each  point is given by (22).
point is given by (22).
( ) Similarly to
) Similarly to  , the differences between adjacent samples in the (
, the differences between adjacent samples in the ( ) plane are not constant, resulting in a nonuniformly sampled frequency space. In order to obtain an evenly sampled spectrum, a new discrete frequency space, denoted by
) plane are not constant, resulting in a nonuniformly sampled frequency space. In order to obtain an evenly sampled spectrum, a new discrete frequency space, denoted by  , is defined. In this space the separation between samples in each
, is defined. In this space the separation between samples in each  plane is
plane is  . Next, the evenly sampled spectrum
. Next, the evenly sampled spectrum is generated by interpolating the data contained in
is generated by interpolating the data contained in  into the frequency values specified in the (
into the frequency values specified in the ( ) space.
) space.
( ) Finally, in order to visualize the reconstructed data in the spatial domain a 3D inverse FFT is applied to
) Finally, in order to visualize the reconstructed data in the spatial domain a 3D inverse FFT is applied to . The result of this process is the 3D model
. The result of this process is the 3D model . A flow diagram of the reconstruction process can be seen in Figure 4.
. A flow diagram of the reconstruction process can be seen in Figure 4.
4. Point Spread Function Analysis
4.1. Preliminaries
The point spread function (psf) is an important analytical tool to assess the spatial constraints of a radar system. This mathematical expression provides a measure of the spatial resolvability of a particular scan geometry and waveform. Additionally, the psf is also used to determine the spatial sampling criteria needed to properly record and reconstruct radar data sets. In general, the point spread function of the p th target along a generic scan trajectory w is modeled as follows:

where  is the support band of the collected responses from the p th target along the w scan direction. The extension of
is the support band of the collected responses from the p th target along the w scan direction. The extension of  is obtained by calculating the difference between the maximum and minimum IF values along each scan trajectory [3]. From basic radar signal theory, it is well known that the support band corresponding to the fast time trajectory t is the same for all the targets in the scan area, or in other words,
is obtained by calculating the difference between the maximum and minimum IF values along each scan trajectory [3]. From basic radar signal theory, it is well known that the support band corresponding to the fast time trajectory t is the same for all the targets in the scan area, or in other words,  , where B is the bandwidth of the radiated waveform. The psf function of a radar signal in the fast time trajectory is given by
, where B is the bandwidth of the radiated waveform. The psf function of a radar signal in the fast time trajectory is given by

The spatial resolution achieved by this psf is equal to

To properly define the psf for a multidimensional SAR system, the support bands along the slow time trajectories must be calculated. Thus, in the following discussion, the behaviour of the psf in the  and z trajectories is analyzed. The corresponding resolution values in both slow-time trajectories are calculated and the corresponding sampling requirements are determined.
and z trajectories is analyzed. The corresponding resolution values in both slow-time trajectories are calculated and the corresponding sampling requirements are determined.
4.2. Angular Scan Trajectory
For the E-CSAR spf, the IF along the  scan direction is given by
scan direction is given by

The maximum IF value is achieved at

where

and the corresponding IF value is

Similarly, it can be shown that the minimum IF value with respect to θ is achieved when  . The IF value in this case is
. The IF value in this case is

Therefore, the value of  is given by
is given by

 is not the same for all the targets in the scan area, because it is a function of the target location and the scan plane. Nevertheless an accurate estimate of the psf mainlobe width can be calculated by using the center value of the domains of
is not the same for all the targets in the scan area, because it is a function of the target location and the scan plane. Nevertheless an accurate estimate of the psf mainlobe width can be calculated by using the center value of the domains of  ,
,  , and
, and  [2]. For a set of fixed R and B values, the average spatial resolution that can be achieved in this support band is given by
[2]. For a set of fixed R and B values, the average spatial resolution that can be achieved in this support band is given by

where  is the radius of the scan area,
is the radius of the scan area,  is the length of the scan geometry along the
is the length of the scan geometry along the  -axis,
-axis,  is the center frequency of the emitted signal, and
is the center frequency of the emitted signal, and

Finally, to avoid the presence of aliasing along the  scan direction in the collected data, the spacing between scan locations in this slow-time direction must be set in such a way that the Nyquist sampling criterion is satisfied. For this purpose, the maximum value that
scan direction in the collected data, the spacing between scan locations in this slow-time direction must be set in such a way that the Nyquist sampling criterion is satisfied. For this purpose, the maximum value that  can achieve must be determined, within the limits imposed by the scan trajectory. A simple way of determining this value is by substituting the upper bound values of the domains corresponding to the
can achieve must be determined, within the limits imposed by the scan trajectory. A simple way of determining this value is by substituting the upper bound values of the domains corresponding to the  ,
,  , and
, and  variables into the right side of (31). The resulting expression is
variables into the right side of (31). The resulting expression is

where

and  is the maximum wavenumber value present in the emitted signal. Therefore, the angular separation between adjacent scan locations along the
is the maximum wavenumber value present in the emitted signal. Therefore, the angular separation between adjacent scan locations along the  scan direction,
scan direction,  , must satisfy the following criterion:
, must satisfy the following criterion:

where  is the minimum wavelength present in the radiated signal.
is the minimum wavelength present in the radiated signal.
4.3. Azimuth Scan Trajectory
The IF of the E-CSAR psf with respect to z is

And the size of the support band is

The support band for this slow time trajectory  is also a function of the target location and the scan angle. In this case we can also use the center values of the domains corresponding to
is also a function of the target location and the scan angle. In this case we can also use the center values of the domains corresponding to  ,
,  ,
,  , and
, and  to define an average value for the support band. Following a similar approach to the one used for (35), the average psf mainlobe size in the z direction (with fixed R and B) values is equal to
to define an average value for the support band. Following a similar approach to the one used for (35), the average psf mainlobe size in the z direction (with fixed R and B) values is equal to

Finally, in order to satisfy the Nyquist criterion in the  scan trajectory, the spacing between scan planes,
scan trajectory, the spacing between scan planes,  , must satisfy the following condition:
, must satisfy the following condition:

5. Results
The performance of the proposed reconstruction approach was assessed using experimental data sets collected from a Stepped Frequency Continuous Wave (SFCW) radar system. The system consists of a 360 B Wiltron network analyzer and an AEL H horn antenna with a length of 19 cm and a height of 12 cm. This antenna is mounted on a support base that is mechanically attached to a mechanism that allows its vertical motion. This mechanism is operated by using a step motor. The support base is made of synthetic low reflective foam. The phantom is mounted into a platform made of maple wood with a height of 25 cm. In order to accurately emulate a cylindrical scan trajectory, the platform is attached to the top of a step motor in order to rotate the phantom. Both step motors are operated using a custom designed control system. This system can communicate to a PC via the serial port in order to specify the desired scan locations. A SFCW waveform with a bandwidth of 11 GHz (1–12 GHz) was used in all the experiments. The system was characterized by recording the reflections of a steel sphere inside an anechoic chamber. The reference signal was subtracted from the experimental data in order to eliminate distortions introduced by the system components. The data acquisition setup was surrounded by electromagnetic wave absorbing material to reduce undesirable reflections from the surrounding environment. The data was reconstructed using a 2.6 GHz dual processor PC with 3 GB RAM.
The phantom used in all the experiments consists of a Polyvinyl Chloride (PVC) pipe filled with synthetic foam disks. The PVC pipe was used as a support structure and has an inner diameter of 10 cm and a height of 90 cm. Aluminum ovoids were used as targets. The ovoids have a 1.2 cm diameter and a 3 cm height. The dielectric permittivity values of the materials used in the support base and the phantom structure are shown in Table 1. A diagram and a photograph of the data acquisition setup can be seen in Figures 5(a) and 5(b), respectively.
The data acquisition process was performed by rotating the phantom at  intervals for a total of 72 positions. Along the
intervals for a total of 72 positions. Along the  -axis, the data was acquired at 15 scan planes with a separation of 1 cm. The value of
-axis, the data was acquired at 15 scan planes with a separation of 1 cm. The value of  in all the experiments was 10 cm. In order to allow the beamwidth to illuminate the entire phantom and reduce undesirable interferences of antenna early time artifacts, the distance between the antenna and the center of the phantom was set to 70 cm. A zero padding factor of 2 was used to improve the visualization of the reconstructed images. In the following discussion, the center of the phantom will be denoted as the origin, and the displayed images show the normalized energy of the reconstructed data. The sampling along the slow time scan trajectories, q and z, was done according to the criteria set in the previous section.
in all the experiments was 10 cm. In order to allow the beamwidth to illuminate the entire phantom and reduce undesirable interferences of antenna early time artifacts, the distance between the antenna and the center of the phantom was set to 70 cm. A zero padding factor of 2 was used to improve the visualization of the reconstructed images. In the following discussion, the center of the phantom will be denoted as the origin, and the displayed images show the normalized energy of the reconstructed data. The sampling along the slow time scan trajectories, q and z, was done according to the criteria set in the previous section.
The data collected from three experimental setups was used to determine the feasibility of the proposed approach and assess its performance. In all the experiments, the separation between the targets was at least equal to twice the value of the spatial resolution along the fast time scan trajectory (1.36 cm). In the first experiment, a single ovoid positioned at ( ) cm was used. A diagram of the experimental setup can be seen in Figure 6. The reconstructed 3D model is shown in Figure 7. In order to have a better visualization of the target signatures, the PVC pipe reflections were removed using the method proposed by the authors in [23]. In the second experiment, two targets were positioned at (0,
) cm was used. A diagram of the experimental setup can be seen in Figure 6. The reconstructed 3D model is shown in Figure 7. In order to have a better visualization of the target signatures, the PVC pipe reflections were removed using the method proposed by the authors in [23]. In the second experiment, two targets were positioned at (0, 2.5,9) cm and (2.5,0,6) cm. The experimental setup can be seen in Figure 8. The reconstructed image viewed from an
2.5,9) cm and (2.5,0,6) cm. The experimental setup can be seen in Figure 8. The reconstructed image viewed from an  plane perspective is shown in Figure 9(a). The corresponding
plane perspective is shown in Figure 9(a). The corresponding  plane perspective view is shown in Figure 9(b). The third experimental setup is shown in Figure 10. In this scan scenario, 3 targets were positioned at (
plane perspective view is shown in Figure 9(b). The third experimental setup is shown in Figure 10. In this scan scenario, 3 targets were positioned at ( 2,2,6) cm, (2.5,2,8.5) cm, and (0,
2,2,6) cm, (2.5,2,8.5) cm, and (0, 2.5,12) cm. The reconstructed 3D model viewed from an
2.5,12) cm. The reconstructed 3D model viewed from an  -axis perspective is shown in Figure 11(a). The corresponding
-axis perspective is shown in Figure 11(a). The corresponding  -axis perspective view is shown in Figure 11(b).
-axis perspective view is shown in Figure 11(b).
To quantitatively assess the performance of the proposed method, the spatial errors of the reconstructed target signatures and the Signal-to-Noise Ratio (SNR) of each reconstructed image were calculated. The SNR of the 3D images was determined as follows:

where  is the magnitude of the 3 dB point of the p th target signature in the 3D model generated by the proposed algorithm and
is the magnitude of the 3 dB point of the p th target signature in the 3D model generated by the proposed algorithm and  is the standard deviation of the background noise. The locations errors of the target signatures and SNR of each reconstructed image are shown in Table 2. Finally, the computational cost of the proposed technique was evaluated. The simulated data sets were generated using the radar simulation tool proposed by the authors in [24]. The execution time of a set of 75 simulated sets was measured. The number of angular scan locations in each plane was 200, and the number of scan planes was set to 21. The order of complexity of the proposed algorithm was
is the standard deviation of the background noise. The locations errors of the target signatures and SNR of each reconstructed image are shown in Table 2. Finally, the computational cost of the proposed technique was evaluated. The simulated data sets were generated using the radar simulation tool proposed by the authors in [24]. The execution time of a set of 75 simulated sets was measured. The number of angular scan locations in each plane was 200, and the number of scan planes was set to 21. The order of complexity of the proposed algorithm was  , where n is the number of data points. This resulted in an average execution time of 10 minutes and 10 seconds (30.5 seconds per plane) for a single data set on the PC used for data processing.
, where n is the number of data points. This resulted in an average execution time of 10 minutes and 10 seconds (30.5 seconds per plane) for a single data set on the PC used for data processing.
6. Conclusions
In this paper, a novel wavefront reconstruction method for E-CSAR data is proposed. The algorithm is based on processing the phase variations exhibited by target reflections along the slow-time trajectories. These differences are used to migrate the target responses from the spatial temporal domain where they are originally collected to a Cartesian space where they are to be displayed. The spectrum of the psf was calculated along the slow-time directions using the stationary phase method. This mathematical approach was chosen because it produces a closed form expression. The mathematical model of the inversion algorithm does not include any terms in the form of Hankel functions, making the proposed reconstruction method computationally efficient.
Theoretical aspects, such as the size of the psf and sampling constraints, were analyzed. In order to determine the experimental feasibility of the proposed method an experimental data acquisition system was assembled. The proposed methods produced spatial accurate imagery with acceptable SNR values at reasonable computational cost. Future research will be concentrated on two main aspects. First, the proposed techniques will be tested on experimental data sets collected from more complex phantoms in order to evaluate their feasibility on more realistic scenarios. Finally, another area of interest is the reduction of the computational cost of the proposed algorithms.
References
Franceschetti G: Synthetic Aperture Radar Processing. CRC Press, Boca Raton, Fla, USA; 1999.
Wehner DR: High-Resolution Radar. Artech House, Norwood, Mass, USA; 2001.
Soumekh M: Synthetic Aperture Radar Signal Processing with MATLAB Algorithms. Wiley-Interscience, New York, NY, USA; 1999.
Sok-Son J, Thomas G, Flores BC: Range-Doppler Radar Imaging and Motion Compensation. Artech House, Norwood, Mass, USA; 2001.
Soumekh M: A system model and inversion for synthetic aperture radar imaging. IEEE Transactions of Image Processing 1992, 1(1):64-76. 10.1109/83.128031
Bryant ML, Gostin LL, Soumekh M: 3-D E-CSAR imaging of a T-72 tank and synthesis of its SAR reconstructions. IEEE Transactions on Aerospace and Electronic Systems 2003, 39(1):211-227. 10.1109/TAES.2003.1188905
Edde B: Radar: Principles, Technology and Applications. Prentice-Hall, Upper Saddle River, NJ, USA; 1995.
Soumekh M: Reconnaissance with slant plane circular SAR imaging. IEEE Transactions on Image Processing 1996, 5(8):1252-1265. 10.1109/83.506760
Curlander J, McDonough R: Synthetic Aperture Radar: Systems and Signal Processing. Wiley-Interscience, New York, NY, USA; 1991.
Ausherman DA, Kozma A, Walker JL, Jones HM, Poggio EC: Developments in radar imaging. IEEE Transactions on Aerospace and Electronic Systems 1984, 20(4):363-400.
Burki J, Barnes CF: Slant plane CSAR processing using householder transform. IEEE Transactions on Image Processing 2008, 17(10):1900-1907.
Fear EC, Stuchly MA: Microwave detection of breast cancer. IEEE Transactions on Microwave Theory and Techniques 2000, 48(1):1854-1863. 10.1109/22.883862
Daian G, Taube A, Birnboim A, Daian M, Shramkov Y: Modeling the dielectric properties of wood. Wood Science and Technology 2006, 40(3):237-246. 10.1007/s00226-005-0060-7
Magnard C, Frey O, Rüegg M, Meier E: Improved airborne SAR data processing by blockwise focusing, mosaicking and geocoding. Proceedings of the 7th European Conference on Synthetic Aperture Radar (EUSAR '08), June 2008 1: 375-378.
Flores-Tapia D, Thomas G, Pistorius S: A wavefront reconstruction method for 3-D cylindrical subsurface radar imaging. IEEE Transactions on Image Processing 2008, 17(10):1908-1925.
Goodman J: Introduction to Fourier Optics. McGraw-Hill, New York, NY, USA; 1968.
Papoulis A: Systems and Transforms with Applications in Optics. McGraw-Hill, New York, NY, USA; 1968.
Stolt RH: Migration by Fourier transform. Geophysics 1978, 43(1):23-48. 10.1190/1.1440826
Milman AS:SAR imaging by
 -
-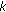 migration. International Journal of Remote Sensing 1993, 14(10):1965-1979. 10.1080/01431169308954015
migration. International Journal of Remote Sensing 1993, 14(10):1965-1979. 10.1080/01431169308954015Lopez-Sanchez JM, Fortuny-Guasch J: 3D radar imaging using range migration techniques. IEEE Transactions on Antennas and Propagation 2000, 48(5):728-737. 10.1109/8.855491
Cafforio C, Prati C, Rocca F: SAR data focusing using seismic migration techniques. IEEE Transactions on Aerospace and Electronic Systems 1991, 27(2):194-207. 10.1109/7.78293
Soumekh M: Band-limited interpolation from unevenly sampled data. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(1):110-122. 10.1109/29.1497
Flores-Tapia D, Thomas G, Phelan M: Clutter reduction of GPR imagery using multiscale products. Proceedings of the IASTED International Conference on Antennas, Radar and Wave Propagation, July 2004 1: 181-185.
Flores-Tapia D, Thomas G, Sabouni A, Noghanian S, Pistorius S: Breast tumor microwave simulator based on a radar signal model. Proceedings of the 6th IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '07), August 2007 1: 17-22.
Acknowledgments
This research was supported by CancerCare Manitoba, Mathematics of Information Technology and Complex Systems, The University of Manitoba, and the Natural Sciences and Engineering Research Council of Canada.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Flores-Tapia, D., Thomas, G. & Pistorius, S. Wavefront Reconstruction of Elevation Circular Synthetic Aperture Radar Imagery Using a Cylindrical Green's Function. EURASIP J. Adv. Signal Process. 2010, 657323 (2009). https://doi.org/10.1155/2010/657323
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/657323











 -
-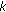 migration. International Journal of Remote Sensing 1993, 14(10):1965-1979. 10.1080/01431169308954015
migration. International Journal of Remote Sensing 1993, 14(10):1965-1979. 10.1080/01431169308954015