- Research Article
- Open access
- Published:
Full Waveform Analysis for Long-Range 3D Imaging Laser Radar
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 896708 (2010)
Abstract
The new generation of 3D imaging systems based on laser radar (ladar) offers significant advantages in defense and security applications. In particular, it is possible to retrieve 3D shape information directly from the scene and separate a target from background or foreground clutter by extracting a narrow depth range from the field of view by range gating, either in the sensor or by postprocessing. We discuss and demonstrate the applicability of full-waveform ladar to produce multilayer 3D imagery, in which each pixel produces a complex temporal response that describes the scene structure. Such complexity caused by multiple and distributed reflection arises in many relevant scenarios, for example in viewing partially occluded targets, through semitransparent materials (e.g., windows) and through distributed reflective media such as foliage. We demonstrate our methodology on 3D image data acquired by a scanning time-of-flight system, developed in our own laboratories, which uses the time-correlated single-photon counting technique.
1. Introduction
In general, laser range finding can be achieved on the basis of triangulation or time-of-flight, of which the latter method is more suited to long-range measurement. In the context of time-of-flight, the principal methodologies include measurement of phase-shift in an amplitude-modulated signal, measurement of frequency shift in a frequency modulated signal, or measurement of transmit-receive pulse separation in a pulsed system [1]. To build a 3D image, either the laser beam must be scanned across the scene, or a static laser beam diverges to encompass the target, and a focal plane array of independent pixels records the received radiation.
Full waveform ladar [2, 3] requires the analysis of multiple returns that occur within a single measurement or pixel. One of the major applications for full waveform topographic ladar analysis is in the survey of forest canopies to monitor environmental changes [4, 5], but this analysis also has important applications in defense and security [6]. One key application is the detection and classification of targets on the ground under tree cover using airborne imagery, which is related to environmental mapping and is the focus of the Jigsaw [7] and Swedish Defence Research [8] systems. However, full waveform analysis is also required in many other situations where single pixel returns are composed of multiple reflections within the laser footprint. For example, this occurs at an occluding boundary, that is, one object behind another, where objects are partially obscured, for example, behind foliage, camouflage, or blinds, when imaging through semitransparent surfaces, or where a single surface may be distributed in depth or moving during exposure. If selected infrared wavelengths are used, then these can penetrate better through the atmosphere or glass [6], and if multiple wavelengths are used, then this be can more informative in surface classification [9, 10].
In many defense and security applications, it is also desirable that the active laser pulse is eye-safe and "covert", that it be of short duration and low energy. To that end, we have developed a 3D imaging ladar system based on a low-power pulsed laser source and a time-correlated single photon counting detector, for which the detailed optical design is described in [11].
The twin demands of low power and multiwaveform analysis place significant demands on the signal processing methodology. Typical techniques within the frequentist framework are to calculate the maximum likelihood estimates (MLE) of parameters for every possible number of signal returns, and then use information theoretic criteria, such as akaike (AIC), bayesian information criterion (BIC) and minimum description length (MDL) [12], to determine the signal number. One popular tool for finding MLE is expectation-maximization (EM) [13]. Compared with centroid method and matched filter, this algorithm is computationally more expensive, but it may give estimates of higher accuracy. However, EM holds a potential risk in that it might converge to a local maximum likelihood [14] or diverge to an infinite value [15]. Additionally, it is sensitive to initial values and not efficient for data set containing numerous observed events, in our case the timing information for the received photons. Moreover, even though AIC, BIC, and MDL introduce penalty terms to avoid overfitting the data, that is adding more returns to increase the likelihood, they still have the tendency to produce more complicated models which correspond to more signal returns [14].
In [16], a hybrid approach is proposed, which first applies a deterministic nonparametric bump-hunting process for initial estimates of signal returns, and second Poisson-MLE to refine the estimates. Although it is effective in many cases, it fails to resolve two closely separated peaks and is not able to produce satisfactory results when the background noise level is comparable or higher than the signal amplitudes.
In order to detect multiple, small returns embedded in background, noise, and clutter, we have been developing concurrently ladar signal analysis methods within the Bayesian framework based on reversible-jump Markov chain Monte Carlo (RJMCMC) techniques for both single pixel and image data [14]. In this paper, we report the development and application of these methods to process images from the new covert, depth imaging sensor, and compare our results with conventional cross-correlation and peak detection applied to the same data.
The organisation of the paper is as follows. In Section 2, we describe briefly the 3D image sensor, and the conditions for data acquisition. In Section 3, we describe the processing methodology. In Section 4, we apply this methodology to images acquired by the sensor to detect wholly visible and partially concealed targets at a moderate range of 325 meters, using our own test facility. We also show how the RJMCMC method can improve our interpretation of the data. Finally, in Section 5, we conclude and summarise some of the key issues that must be addressed to develop these ideas further.
2. The Ladar Imaging System
In a time-correlated single photon counting (TCSPC) ranging system, the general principle is to direct a pulsed laser beam towards the target and to collect and record the times of arrival (since pulse transmission) of the back-scattered photons. Hence, the distance to the target ( ) can be computed, and knowing the geometry of the imaging system the direction of the transmitted laser signal can be used to compute the
) can be computed, and knowing the geometry of the imaging system the direction of the transmitted laser signal can be used to compute the  coordinates. This basic principle is applicable to both scanning systems, such as our own, and to arrays of single photon counting detectors such as that reported by Sudharasan et al. [17]. While arrayed detectors provide parallel data acquisition, which has clear advantages in acquiring data from moving targets and in eliminating scanning components, there are problems with crosstalk and fill-factor. In general, we can achieve better temporal response and sensitivity with a single element detector, which is of considerable importance for covert, low-power operation. The system of interest is illustrated in Figure 1(a).
coordinates. This basic principle is applicable to both scanning systems, such as our own, and to arrays of single photon counting detectors such as that reported by Sudharasan et al. [17]. While arrayed detectors provide parallel data acquisition, which has clear advantages in acquiring data from moving targets and in eliminating scanning components, there are problems with crosstalk and fill-factor. In general, we can achieve better temporal response and sensitivity with a single element detector, which is of considerable importance for covert, low-power operation. The system of interest is illustrated in Figure 1(a).
(a) Schematic diagram indicating the principal components of the scanning system. Electrical paths are denoted by solid lines, optical paths by dashed lines. Si-SPAD is a silicon single-photon avalanche diode. (b) The transceiver head assembly. The system dimensions are approximately 275 mm by 275 mm by 175 mm. The two galvanometer servo-control circuit boards (not visible) are on the underside of the slotted baseplate.
The system uses a pulsed semiconductor diode laser, of pulse half-width 90 ps, operating at 842 nm wavelength, that emits low energy pulses ( 30 pJ). The laser is capable of operating at repetitions rates in excess of 10 MHz, although 2 MHz was the maximum rate used in these measurements. Scene scanning is performed by a pair of galvanometer mirrors. The optical system is used to direct the outgoing laser pulses onto each optical field position of the target, and also to efficiently collect the scattered photons returned from each corresponding pixel of the imaged scene. The collected return photons are routed using polarisation optics to an individual, high performance single-photon detector module via a single mode optical fiber. The signal from the single-photon detector is recorded as a timed photon event, equivalent to range (
30 pJ). The laser is capable of operating at repetitions rates in excess of 10 MHz, although 2 MHz was the maximum rate used in these measurements. Scene scanning is performed by a pair of galvanometer mirrors. The optical system is used to direct the outgoing laser pulses onto each optical field position of the target, and also to efficiently collect the scattered photons returned from each corresponding pixel of the imaged scene. The collected return photons are routed using polarisation optics to an individual, high performance single-photon detector module via a single mode optical fiber. The signal from the single-photon detector is recorded as a timed photon event, equivalent to range ( ) which can be associated with an
) which can be associated with an  coordinate that is known from the calibrated scanning optics. For the particular optical configuration and scanning parameters used in these measurements, the maximum field of view was 55 mrad and the beam width and scanning resolution were both approximately 23 mm at a standoff distance at 325 m. In general, each detector event records a photon arrival of which some will be returned from the target, some from stray events (other light sources), and some will be due to detector, dark counts. To reduce the stray photon events, our system includes spatial filtering (by coupling into the single mode optical fiber), spectral filtering (by narrowband filtering at the known laser wavelength) and temporal filtering (by the TCSPC technique, as there is finite window in which to record a photon event). Timing uncertainty is introduced by jitter in the master clock, the laser driver, the detector (silicon SPAD) and the timing electronics. For all those reasons, we use many pulses to build up a statistical distribution of the number of recorded photon arrivals as a function of the arrival time. This can be interpreted as a range measurement, and by scanning and recording distributions at each pixel, as a depth image. An example of a measurement that records data from more than one surface in the field of view of a single pixel is shown in Figure 2.
coordinate that is known from the calibrated scanning optics. For the particular optical configuration and scanning parameters used in these measurements, the maximum field of view was 55 mrad and the beam width and scanning resolution were both approximately 23 mm at a standoff distance at 325 m. In general, each detector event records a photon arrival of which some will be returned from the target, some from stray events (other light sources), and some will be due to detector, dark counts. To reduce the stray photon events, our system includes spatial filtering (by coupling into the single mode optical fiber), spectral filtering (by narrowband filtering at the known laser wavelength) and temporal filtering (by the TCSPC technique, as there is finite window in which to record a photon event). Timing uncertainty is introduced by jitter in the master clock, the laser driver, the detector (silicon SPAD) and the timing electronics. For all those reasons, we use many pulses to build up a statistical distribution of the number of recorded photon arrivals as a function of the arrival time. This can be interpreted as a range measurement, and by scanning and recording distributions at each pixel, as a depth image. An example of a measurement that records data from more than one surface in the field of view of a single pixel is shown in Figure 2.
3. Full Waveform Ladar Analysis Based on RJMCMC
3.1. Bayesian Modelling of Ladar Signals
In previous work, we have shown how Bayesian analysis (using the reversible jump markov chain monte carlo (RJMCMC) computational methodology [18]) can be used to construct multilayered 3D images [14] when the laser return consists of multiple peaks due to the footprint of the beam impinging on a target with surfaces distributed in depth. In dense ladar images, one can improve the quality of the 3D data by considering spatial context through a markov random field (MRF) [19]. We have also shown how multispectral LiDAR can be used to classify different types of surface response on the basis of different colour responses, using a maximum of six wavelengths [10]. We have applied these techniques successfully to both Burst Illumination Laser (BIL) [20] and TCSPC [21] ladar systems. As pointed out by Mallet and Bretar [3] in their survey on full waveform LiDAR for remote sensing, our RJMCMC method is robust (finding a global minimum in a multimodal distribution), no initialization or gradient computations are required, and the grammar of instrumental models is extensible.
To interpret this data, we use a piecewise, exponential model for the Si-SPAD return, first introduced in [22] because it has the appropriate shape parameters to model the physical transport processes within the Si-SPAD detector. The parametric form of the expected temporal variation of the photon count distribution is given by

where  is an amplitude factor,
is an amplitude factor,  is the time of the peak maximum, and
is the time of the peak maximum, and  ,
,  and
and  are the points at which the changeovers between functions occur as shown in Figure 3(b). In this study, we assume that the shape parameters are fixed and known from the instrumental response. Hence, we only need to compute the amplitude and time of arrival, measures of reflectance and distance, respectively.
are the points at which the changeovers between functions occur as shown in Figure 3(b). In this study, we assume that the shape parameters are fixed and known from the instrumental response. Hence, we only need to compute the amplitude and time of arrival, measures of reflectance and distance, respectively.
(a) A single magnified selected peak from Figure 2. (b) Instrumental response of TCSPC ladar signal (dotted line) and fitting result (solid line) using piecewise exponential model with fitting errors (dashed line). The parameter sets corresponding to (1) are:  .
.
For full waveform ladar, multiple returns are observed against a background level whose expected value is constant across all bins of the photon (intensity) histogram,  . This is considered as a sample of a nonnormalized statistical mixture distribution with density
. This is considered as a sample of a nonnormalized statistical mixture distribution with density

where  is the number of peaks,
is the number of peaks,  is the background and
is the background and  is the set of parameters of each signal and the background:
is the set of parameters of each signal and the background:  with
with  and
and  .
.  is defined by (1). The number of photons recorded,
is defined by (1). The number of photons recorded,  , in each channel
, in each channel  is considered as a random sample of a Poisson distribution with intensity
is considered as a random sample of a Poisson distribution with intensity  ,
,

Assuming that the observations recorded in each channel  of the histogram are conditionally independent given the value of the parameters, the joint probability distribution of
of the histogram are conditionally independent given the value of the parameters, the joint probability distribution of  is defined as
is defined as

In the Bayesian paradigm, our goal is to find the posterior distribution of the number, positions, and amplitudes of the multiple returns in the full waveform ladar signal. The posterior distribution is defined as

where the likelihood function,  is defined by (4) and the full joint prior distribution is given by
is defined by (4) and the full joint prior distribution is given by  .
.
3.2. RJMCMC Methodology for Ladar Signal Analysis
We follow the methodology described in [14] by constructing a Markov chain whose transitions involve changes to the number, positions, and amplitudes of peaks in the return signal. Hence, we consider the histogram as a discrete representation of a spatially heterogeneous Poisson process whose intensity is a linear superposition of the scaled and shifted returns as defined in (2). In the RJMCMC paradigm, the transitions of the Markov chain involve several moves within a single "sweep".
-
(1)
Updating the positions
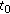 .
. -
(2)
Updating the amplitudes
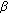 .
. -
(3)
Updating the background
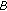 .
. -
(4)
Random birth or death of a peak.
-
(5)
Random splitting of a peak into two peaks or merging of two peaks into a single peak.
At each iteration of the chain, we follow the Metropolis-Hastings algorithm. Moves of type (1), (2), and (3) allow the posterior distribution to be explored within a state space with a fixed dimension,  . The Metropolis-Hastings method draws the proposed values from an arbitrary proposal probability distribution
. The Metropolis-Hastings method draws the proposed values from an arbitrary proposal probability distribution  . These values are accepted with probability
. These values are accepted with probability  , otherwise they are rejected and the existing values are retained. The acceptance probability is expressed as
, otherwise they are rejected and the existing values are retained. The acceptance probability is expressed as

In this case,  can be
can be  ,
,  , or
, or  dependent on whether it is a move of type (1), (2) or (3).
dependent on whether it is a move of type (1), (2) or (3).
For full waveform ladar, we do not know the value of  , so the state space becomes a set of parameter subspaces with different dimensionality. Since both
, so the state space becomes a set of parameter subspaces with different dimensionality. Since both  and
and  are subject to inference, it is necessary to compare the different models while learning about the parameters within each model. Therefore, we use the RJMCMC algorithm, which allows jumps between subspaces for different
are subject to inference, it is necessary to compare the different models while learning about the parameters within each model. Therefore, we use the RJMCMC algorithm, which allows jumps between subspaces for different  in addition to within-model parameter updates for a particular
in addition to within-model parameter updates for a particular  , that is steps (4) and (5) above. Still following the Metropolis-Hastings procedure, the target distribution now becomes
, that is steps (4) and (5) above. Still following the Metropolis-Hastings procedure, the target distribution now becomes  and the acceptance probability becomes
and the acceptance probability becomes

where  is the probability of move type
is the probability of move type  when in state
when in state  ,
,  is the density function of a continuous random vector
is the density function of a continuous random vector  and the Jacobian term
and the Jacobian term  arises from deterministic transfer from variable
arises from deterministic transfer from variable  to
to  .
.
3.3. Convergence Assessment
A properly designed Markov chain Monte Carlo sampler should generate a convergent Markov sequence whose limiting distribution is the true joint posterior distribution of interest [23]. However, in practical applications, only a finite number of samples can be produced, and it is therefore important to choose the chain length appropriately and assess the convergence of the Markov chain to the stationary distribution.
Three separate but related issues need to be considered when determining the chain length [24, 25]. First, evaluate the length of the burn-in period, which is to determine from which observation point the chain has "forgotten" its starting value and escaped from its influence. At this point, the chain has reached the stationary distribution and the previous samples should be discarded to eliminate the estimation bias introduced by the transient period. Second, determine if the chain is long enough to fully represent the underlying distribution and conclude its convergence to an asymptotic distribution. Third, evaluate if the samples are adequate to achieve a certain precision of estimation.
Over the last two decades, a number of different convergence diagnostics have been proposed, which can be classified into two categories. For theoretical approaches, the attempt is to predetermine the number of iterations required to ensure convergence by analyzing the Markov transition kernel and stationary distribution; a collection of approaches can be found in [26, 27] and references therein. Although they hold formal guarantees, these algorithms are not feasible in practice due to sophisticated mathematical calculation and loose convergence bounds. Therefore, as pointed out in [26], empirical methods are almost always applied, relying on the outputs of MCMC samplers and diagnostics computed from the produced sequence to check convergence. On the one hand, they provide evidence of convergence; on the other hand, all the diagnostics are unreliable since in practice the target limiting distribution always remains unknown and it is impossible to conclude with certainty that the finite MCMC samples are sufficient to cover the whole support of the underlying stationary distribution. From this point of view, we should be cautious about the diagnostic results.
In the literature, empirical methods seek to conclude the convergence through bias and/or variance evaluation. The Gelman and Rubin diagnostic methodology presented in [23, 28] compares the samples drawn from several independent sequences with different starting points and quantitatively evaluates mixing by analyzing the within-sequence and between-sequence variance. The estimation bias arising from the produced samples is uncovered by multiple separate chains rather than a single chain, and therefore it has comparatively higher diagnostic reliability in terms of detecting if the underlying stationary distribution has been fully explored and the chains have converged to the same limiting distribution. This is particularly significant when applied to multimodal posterior distributions.
The idea of the Gelman and Rubin method is that as the number of samples increases, each individual chain will explore larger parts of the parameter space, and consequently, the overall and within-sequence variances will both converge to the true model variance. Assume that we simulate  independent sequences initialized with over dispersed starting points, each of length
independent sequences initialized with over dispersed starting points, each of length  , and discard the first
, and discard the first  samples as the burn-in period. For any scalar function
samples as the burn-in period. For any scalar function  , we label the
, we label the  th observation in chain
th observation in chain  as
as  and calculate the between-sequence variance
and calculate the between-sequence variance 

where

The within-sequence variance  is estimated by
is estimated by

where

The variance of  in the target distribution,
in the target distribution,  is estimated by
is estimated by

The convergence of the Markov chain is monitored by the estimated potential scale reduction factor (PSRF)

As  , the total variance estimation
, the total variance estimation  should decrease while the within-sequence variance
should decrease while the within-sequence variance  should increase, and finally the PSRF should theoretically decline to 1. If
should increase, and finally the PSRF should theoretically decline to 1. If  is large, it indicates the posterior distribution should be further explored. Once the PSRF is close to 1, we assume the Markov chain has converged to the target distribution.
is large, it indicates the posterior distribution should be further explored. Once the PSRF is close to 1, we assume the Markov chain has converged to the target distribution.
4. Experimental Comparison: Cross-Correlation, MCMC and RJMCMC
In this section, we present the analysis of images acquired under bright daylight conditions of two distant outdoor scenes, comparing methods based on cross-correlation and fixed and variable dimension Markov chain Monte Carlo analysis. Our images are of a life-sized mannequin (a human figure) in full view of the sensor, and of the same mannequin partially concealed behind a fence. The data were acquired at a range of approximately 325 meters. The equivalent scene dimensions were 0.8 m width by 2.0 m height, and the scanned image resolution was 32 by 128 pixels for the whole mannequin. The pulse repetition frequency was 2 MHz, resulting in an average optical power of 40  W. The pixel dwell time was 1.0 s.
W. The pixel dwell time was 1.0 s.
To assess the ability of RJMCMC algorithm for multiple peak detection and particularly the resolution capacity for closely separated peaks, we set up a remote target containing several distributed surfaces with known separations, which provides the ground truth and allows us to compare the performance with cross-correlation method.
4.1. Mannequin in Full View: Cross-Correlation and MCMC
In the first example, the mannequin is in full view, standing in front of a concrete pillar, as shown in Figure 5. It was anticipated that the majority of pixels would have clear and distinct, single returns from the surface of either the mannequin or the pillar. Given the divergence of the beam there may be some mixed pixels at the occluding boundary of the mannequin, and there may be pixels with no return as they miss the targets all together. In short, this is a situation in which a cross-correlation detector based on the system instrumental response should perform well and there should be questionable need for the added complexity of Markov chain Monte Carlo analysis. Further, since the expectation in processing this data set is to estimate the range of a single surface return from either the mannequin or the pillar, we apply the fixed dimension Markov chain Monte Carlo (MCMC) approach to avoid redundant computation caused by trans-dimension jumps. Accordingly, only the first three steps in Section 3.2 are used.
The unknowns ( ) subject to inference have independent priors. To completely eliminate any prior knowledge of the peak position,
) subject to inference have independent priors. To completely eliminate any prior knowledge of the peak position,  is drawn from a uniform distribution on
is drawn from a uniform distribution on  . The peak amplitudes (
. The peak amplitudes ( ) and background (
) and background ( ) follow Gamma distributions
) follow Gamma distributions  and
and  with the shape parameters
with the shape parameters  set to be
set to be  and
and  , while the scale parameters
, while the scale parameters  are
are  and
and  respectively, where
respectively, where  is the histogram of photon counts. The previously unspecified proposal distributions are set as follows: all of the parameter updates employ the Gaussian random walk whose proposal means are the current sample values. The standard deviations for amplitude (
is the histogram of photon counts. The previously unspecified proposal distributions are set as follows: all of the parameter updates employ the Gaussian random walk whose proposal means are the current sample values. The standard deviations for amplitude ( ) and background (
) and background ( ) are both 0.3. For position updates, a delayed rejection step [14] is carried out to allow movement between posterior estimates that correspond to more widely separated channels. When using delayed rejection, the scale in each step is characterized by
) are both 0.3. For position updates, a delayed rejection step [14] is carried out to allow movement between posterior estimates that correspond to more widely separated channels. When using delayed rejection, the scale in each step is characterized by  and
and  respectively.
respectively.
We first generate multiple chains for each pixel and evaluate the convergence. After finding a safe convergence length, we then run single MCMC chains with  on all the pixels with a bounded number of iterations (5000) including the 500 samples burn-in period. This is consistent with the initial estimate. Subsequently, to assess the convergence of the MCMC chains, we produce four independent sequences for each pixel, and monitor the Gelman and Rubin diagnostic statistic (PSRF) defined in Section 3.3 every 100 samples. The chain generation is terminated when the convergence is concluded, that is when the PSRF reduces to less than a preset threshold
on all the pixels with a bounded number of iterations (5000) including the 500 samples burn-in period. This is consistent with the initial estimate. Subsequently, to assess the convergence of the MCMC chains, we produce four independent sequences for each pixel, and monitor the Gelman and Rubin diagnostic statistic (PSRF) defined in Section 3.3 every 100 samples. The chain generation is terminated when the convergence is concluded, that is when the PSRF reduces to less than a preset threshold  , at which the posterior distributions
, at which the posterior distributions  obtained from all the sample trajectories becomes approximately the same.
obtained from all the sample trajectories becomes approximately the same.
Figure 4(a) presents a representative pixel with a single distinct return. For this type of pixel data, there is a clear, sharp peak in the normalised cross correlation plot and a distinct preference in the frequency of positions obtained from MCMC sequences. Their maximum values are both located in the same channel index as shown in Figure 4(c). In this circumstance, the cross-correlation approach can easily detect the surface return, and according to Figure 4(d), MCMC chains can converge rapidly with a small number of samples (about 500 samples after the burn-in period) due to the simplicity of parameter space.
Analysis of time-of-flight ladar data, in which the histogram bins have been converted to relative depth in meters. The first column shows the raw pixel data (in blue). The second column magnifies the plots of signal peaks in the first column. The third column shows the normalized cross-correlation values (blue curves) and the frequencies of positions (black bars) obtained from the MCMC samplers. The last column tracks the corresponding PSRF values against the number of samples. The final fit estimations (from MCMC) are the red curves in the first column.
32 × 128 pixel image of a life-sized mannequin scanned at a distance of 325 m in daylight conditions. (a) Photograph of the 1.8 m tall mannequin in the scan position. (b) and (c) Three-dimensional plots of the processed depth information using the cross-correlation and MCMC methods, respectively. Empty pixels in the plots contained depth values outside the displayed range. The lower number of missing pixels in (c) on noncooperative target surfaces with low reflectance, especially the mannequin's trousers, demonstrate the MCMC algorithm's advantage in resolving low-intensity returns.
For the low-amplitude return in Figure 4(e), the cross-correlation approach gives several extrema as displayed in Figure 4(g). Such low amplitude may be caused primarily by lower reflectance back towards the receiver, either because of the material properties or its angle to the beam direction. In this case, it is difficult to decide with certainty where the surface return is located, although we can always define it to be the one corresponding to the maximum cross-correlation value. In comparison, the power of the MCMC methodology lies in supplying Bayesian evidence of the final answer. In other words, the histogram of  indicates the posterior distribution of the estimates. As the parameter space becomes more complex, the posterior distribution is spread over a wider channel range and becomes bimodal, which in turn results in a slower convergence rate and an increased chain length in excess of 4000 samples.
indicates the posterior distribution of the estimates. As the parameter space becomes more complex, the posterior distribution is spread over a wider channel range and becomes bimodal, which in turn results in a slower convergence rate and an increased chain length in excess of 4000 samples.
Another example is shown in Figure 4(k). For this pixel, the bin index for the maximum cross-correlation does not equal the one for the  posterior mode. Hence, the MCMC chain gives a different and better substantiated estimate of the true value, further demonstrating the power of the Bayesian approach.
posterior mode. Hence, the MCMC chain gives a different and better substantiated estimate of the true value, further demonstrating the power of the Bayesian approach.
3D images based on these two methods are provided in Figure 5, where a target range gate is set and those pixels with with target position estimates beyond this preset gate are treated as zero return. It is observed that there are a few more pixels beyond the target range with cross-correlation, which implies the maximum values do not always correspond to the correct surface position. This is consistent with the discussion of illustrative pixel data showing the strength of the MCMC method in processing low amplitude ladar signals hidden in backgrounds in that the posterior mode is more informative, robust, and reliable.
4.2. Mannequin Concealed by Fence: Cross-Correlation and RJMCMC
In the next example, a wooden fence is placed approximately 1 meter in front of the mannequin, as shown in Figure 6. The image resolution of the scanned upper half mannequin is 32 by 48 pixels. Because of the area of the laser footprint, it is highly likely that some pixels may observe multiple reflections composed of some or all of the fence, the mannequin, and the pillar behind, where the beam hits occluding boundaries. In this situation, determination of the number of surfaces is an additional crucial issue and so we apply the RJMCMC method to obtain varying-dimensional ladar signal analysis.
In one sweep of the RJMCMC algorithm, the fixed-dimensional parameter updates (steps 1–3 of Section 3.2) follow the MCMC sampler settings. Jumps between parameter subspaces with different dimensions are accomplished by steps 4 and 5 in the same manner as [14]. Although our expectation would be that the number of surface returns in any single pixel would not be greater than three in this example, we are conservative in allowing the varying dimension sampler to explore  values from
values from  to
to  .
.
Figure 7 illustrates representative pixels containing zero, one (either mannequin or fence), two (fence and mannequin) or three returns (fence, mannequin, and pillar), with the corresponding photon counts histogram, unified cross-correlation values,  estimates and fitting results from the RJMCMC sampler.
estimates and fitting results from the RJMCMC sampler.
Comparison of ladar signal analysis for the concealed mannequin using RJMCMC and cross-correlation. The first column shows the raw data and the posterior parameter estimates from the RJMCMC method, while the second column gives the magnified plot of the signal peaks. The third column shows the cross-correlation function. The right hand column shows the posterior probability estimate of the number of surface returns,  .
.
The first row of Figure 7 illustrates a pixel in which the beam misses all three targets, so that no surface return exists. The use of the cross-correlation method is difficult when there is no surface return as shown in Figure 7(a) to 7(d). In comparison with Figure 4(g) from a small signal-to-background ratio pixel, Figure 7(c) shows the probable existence of at least one surface return. However, according to the asymptomatic posterior probability estimate of  , no target return is the most probable conclusion. If we examine the second and third rows of Figure 7 then we see the situations analogous to Figure 4(e) in that there are single returns from fence and mannequin, respectively. The difference in this case is that we have applied full RJMCMC chains, so that the posterior probability estimate,
, no target return is the most probable conclusion. If we examine the second and third rows of Figure 7 then we see the situations analogous to Figure 4(e) in that there are single returns from fence and mannequin, respectively. The difference in this case is that we have applied full RJMCMC chains, so that the posterior probability estimate,  , shows one return.
, shows one return.
Of more interest are those pixels containing more than one return, shown in Figures 7(m)–7(x). The fourth row has distinct returns from the fence and mannequin, and the RJMCMC sampler has a very strong preference for two returns. The fifth row is far less distinct, but the sampler again shows a strong posterior probability estimate of two peaks, although the second one might be difficult to detect automatically on a cross-correlation detector, for example, using a fixed (or even proportional) threshold. Due to the varying surface reflectances and angles, pixels can have different photon intensities, which makes it a difficult problem to choose a reliable threshold. The corresponding parameter estimates of the two surface returns shown in Figure 7(q) correspond in depth to the known ground truth of the relative separation. Finally, the last row shows one of the pixels in which the beam partially reflects from the fence, partially transmits through a gap and hence reflects from the mannequin, but near an occlusion boundary so that part reflects from the pillar behind. The posterior estimate of  favours
favours  surfaces but it is by no means as clear cut as the earlier examples, and the parameter estimates of the 3 surface positions shown in Figure 7(u) correspond to the fence, mannequin, and pillar separations at this point.
surfaces but it is by no means as clear cut as the earlier examples, and the parameter estimates of the 3 surface positions shown in Figure 7(u) correspond to the fence, mannequin, and pillar separations at this point.
To better illustrate the posterior estimates of the number of surfaces,  , Figure 8 shows those pixels in which
, Figure 8 shows those pixels in which  and
and  surfaces were estimated. Physically, one expects no returns when the laser hits no surface, or where the surface angle is so oblique (e.g., at the extremities of the pillar) that no return is likely. In this image, these are primarily where the beam goes through the fence but above both mannequin and pillar. When
surfaces were estimated. Physically, one expects no returns when the laser hits no surface, or where the surface angle is so oblique (e.g., at the extremities of the pillar) that no return is likely. In this image, these are primarily where the beam goes through the fence but above both mannequin and pillar. When  it hits a single surface, and when
it hits a single surface, and when  , two surfaces, as described above. There are only a few pixels for which
, two surfaces, as described above. There are only a few pixels for which  , where the beam grazes the left arm, and no estimates of
, where the beam grazes the left arm, and no estimates of  . Figure 9 shows a surface plot of the meshed
. Figure 9 shows a surface plot of the meshed  data for the 3D image of the partially concealed mannequin behind the fence. As the mannequin surface has been interpolated and smoothed from the raw data values it should be considered as illustrative, but there was no necessity for outlier removal, and the shape of the upper body is relatively well defined.
data for the 3D image of the partially concealed mannequin behind the fence. As the mannequin surface has been interpolated and smoothed from the raw data values it should be considered as illustrative, but there was no necessity for outlier removal, and the shape of the upper body is relatively well defined.
4.3. Real Data with Known Geometry: Cross-Correlation and RJMCMC
We set up a remote target at a range of approximately 325 meters, which contained 6 distributed surfaces with separations between adjacent surfaces of  450, 10, 200, 30, and 90 mm
450, 10, 200, 30, and 90 mm . The photon counting histogram in Figure 10 was collected with the scanning system using a 3 MHz pulse repetition frequency and 50
. The photon counting histogram in Figure 10 was collected with the scanning system using a 3 MHz pulse repetition frequency and 50  W average laser power, the bin resolution was 4 ps. The RJMCMC sampler used here is exactly the same as the one for the fence data but allows
W average laser power, the bin resolution was 4 ps. The RJMCMC sampler used here is exactly the same as the one for the fence data but allows  to vary from 0 to 10.
to vary from 0 to 10.
Analysis of TCSPC data from a real target containing 6 distributed surfaces with known separation distances: {450, 10, 200, 30, and 90 mm}. The blue line gives the 5 peaks detected by RJMCMC method with separations determined to be {452.4, 207.6, 27, and 100.2 mm}. The green line is the cross-correlation of the signal (for the sake of display clarity, the maximum value is scaled to be 6), which gives 4 peaks with separations {454.8, 225.6, and 97.8 mm}.
According to Figure 10, both RJMCMC and cross-correlation methods succeed in detecting distinct return signals. For the two surfaces separated at 30 mm, they merge to be a single peak in cross-correlation values. In comparison, with assistance of Merge/Split updates, RJMCMC can easily separate them. However, both methods fail to distinguish the peaks 10 mm (17 channel bins) away from one another, and instead place a combined return, which results in the increased estimated distances from the combined signal to its neighboring peaks, that is, the two peaks corresponding to the surfaces separated by 450 and 200 mm.
5. Conclusions and Future Work
In this paper, we have demonstrated the application of Bayesian analysis using Markov chains to analyse full-waveform Ladar pixel and image data acquired by a new scanning sensor. The sensor uses time-correlated photon counting technology, and coupled with algorithmic development, we are able to detect multiple surface returns within the field of view of single pixels, creating multilayer images. This has application in defence and security when objects of interest may be partially concealed, or viewed through semitransparent surfaces, such as through windows.
To demonstrate the method, and compare with thresholded correlation analysis, we have used selected data from two images of a distant target, the first in full view, the second viewed through a trellis fence. In general, RJMCMC analysis is advantageous in supplying principled estimates of both the number of surface returns and the associated parameter vectors (range, amplitude, and background level). This allows us to construct multilayered 3D images. The methodology is effective in dealing with low amplitude returns, a few photons at maximum in a single bin. This adds to the covert capability of the sensor, aimed at detecting returns from uncooperative surfaces at medium range using a low-power source laser diode.
However, there are a number of outstanding problems that require future work. In the long term, we need to acquire image data at an approximate rate of one frame per second, or better, and to process the data in comparable time frames. Currently, we are investigating the use of convergence diagnostics to better control the chain length, the validity of initialising the chains by correlation data, and multicore programming in combination with vector processor and FPGA technology. In general, all of these can lead to faster, single pixel processing. Another possibility is to promote an investigation on the Dirichlet process (DP) mixture model developed in [29] and recently studied in [30], which provides natural estimates for Bayesian inference in both model number and associated parameters with efficient simulations.
References
Amann M-C, Bosch T, Lescure M, Myllylä R, Rioux M: Laser ranging: a critical review of usual techniques for distance measurement. Optical Engineering 2001, 40(1):10-19. 10.1117/1.1330700
Wagner W, Ullrich A, Ducic V, Melzer T, Studnicka N: Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS Journal of Photogrammetry and Remote Sensing 2006, 60(2):100-112. 10.1016/j.isprsjprs.2005.12.001
Mallet C, Bretar F: Full-waveform topographic lidar: State-of-the-art. ISPRS Journal of Photogrammetry and Remote Sensing 2009, 64(1):1-16. 10.1016/j.isprsjprs.2008.09.007
Véga C, St-Onge B: Height growth reconstruction of a boreal forest canopy over a period of 58 years using a combination of photogrammetric and lidar models. Remote Sensing of Environment 2008, 112(4):1784-1794. 10.1016/j.rse.2007.09.002
Hosoi F, Omasa K: Estimating vertical plant area density profileand growth parameters of a wheat canopy at different growth stagesusing three-dimensional portable lidar imaging. ISPRS Journal of Photogrammetry and Remote Sensing 2009, 64: 151-158. 10.1016/j.isprsjprs.2008.09.003
Letalick D, Chevalier T, Larsson H: 3D imaging of partly concealed targets by laser radar. Division of Sensor Technology, the Swedish Defence Research Agency; October 2005.
Ludwig D, Kongable A, Krywick S, et al.: Identifying targets under trees—Jigsaw 3D-LADAR test results. Laser Radar Technology and Applications VIII, 2003, Proceedings of SPIE 5086: 16-26.
Gronwall C, Chevalier T, Tolt G, Andersson P: An approach to target detection in forested scenes. Laser Radar Technology and Applications XIII, 2008, Proceedings of SPIE 6950: S1-S12.
Voss M, Sugumaran R: Seasonal effect on tree species classification in an urban environment using hyperspectral data, LiDAR, and an object-oriented approach. Sensors 2008, 8(5):3020-3036. 10.3390/s8053020
Wallace AM, Buller GS, Sung RCW, Harkins RD, McCarthy A, Hernandez-Marin S, Gibson GJ, Lamb R: Multi-spectral laser detection and ranging for range profiling and surface characterization. Journal of Optics A 2005, 7(6):S438-S444. 10.1088/1464-4258/7/6/028
McCarthy A, Collins RJ, Krichel NJ, Fernandez V, Wallace AM, Buller GS: Long-range time of flight scanning sensor based on high speed time-correlated photon counting. Applied Optics 2009, 48(32):6241-6251. 10.1364/AO.48.006241
Schwarz G: Estimating the dimension of a model. Annals of Statistics 1978, 6: 461-464. 10.1214/aos/1176344136
Dempster AP, Laird NM, Rubin D: Maximum likelihood from incomplete data via the EM algorithm (with discussion). Journal of the Royal Statistical Society Series B 1977, 39: 1-38.
Hernández-Marín S, Wallace AM, Gibson GJ: Bayesian analysis of lidar signals with multiple returns. IEEE Transactions on Pattern Analysis and Machine Intelligence 2007, 29(12):2170-2180.
Fraley C, Raftery AE: Bayesian regularization for normal mixture estimation and model-based clustering. Journal of Classification 2007, 24(2):155-181. 10.1007/s00357-007-0004-5
Wallace AM, Sung RCW, Buller GS, Harkins RD, Warburton RE, Lamb RA: Detecting and characterizing returns in amulti-spectral pulsed lidar system. IEE Proceedings-Vision Image and Signal Processing 2006, 153(2):160-172. 10.1049/ip-vis:20045023
Sudharasan R, Yuan P, Boisvert J, et al.: Single photon counting Geiger mode InGaAs(P)/InP avalanche photodiode arrays for 3D imaging. Laser Radar Technology and Applications XII, 2008, Proceedings of SPIE 6950: 69500N.
Green PJ: Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 1995, 82: 711-732. 10.1093/biomet/82.4.711
Hernandez-Marin S, Wallace AM, Gibson GJ: Multilayered 3D LiDAR image construction using spatial models in a Bayesian framework. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008, 30(6):1028-1040.
Duncan S, Cople J, Harvey G, Humphreys D, Gonglewski J, Baker I: Advances in laser gated imaging in an airborne environment. Infrared Technology and Applications XXXII, April 2006, Proceedings of SPIE 6206: 650607.
Buller GS, Wallace AM: Ranging and three-dimensional imaging using time-correlated single-photon counting and point-by-point acquisition. IEEE Journal on Selected Topics in Quantum Electronics 2007, 13(4):1006-1015.
Pellegrini S, Buller GS, Smith JM, Wallace AM, Cova S: Laser-based distance measurement using picosecond resolution time-correlated single-photon counting. Measurement Science and Technology 2000, 11(6):712-716. 10.1088/0957-0233/11/6/314
Gelman A: Markov Chain Monte Carlo in Practice: Interdisciplinary Statistics. Chapman & Hall/CRC, Boca Raton, Fla, USA; 1995.
El Adlouni S, Favre A-C, Bobée B: Comparison of methodologies to assess the convergence of Markov chain Monte Carlo methods. Computational Statistics and Data Analysis 2006, 50(10):2685-2701. 10.1016/j.csda.2005.04.018
Giakoumatos SG, Vrontos ID, Dellaportas P, Politis DN: A Markov chain Monte Carlo convergence diagnostic using subsampling. Journal of Computational and Graphical Statistics 1999, 8(3):431-451. 10.2307/1390868
Cowles MK, Carlin BP: Markov chain Monte Carlo convergence diagnostics: a comparative review. Journal of the American Statistical Association 1996, 91(434):883-904. 10.2307/2291683
Mengersen K, Knight S, Robert CP: MCMC: how do we know when to stop? 1999.http://www.stat.fi/isi99/proceedings/arkisto/varasto/meng0251.pdf
Gelman A, Rubin DB: Inference from iterative simulation using multiple sequences. Statistical Science 1992, 7(4):457-472. 10.1214/ss/1177011136
Escobar MD, West M: Bayesian density-estimation and inference using mixtures. Journal of the American Statistical Association 1995, 90: 577-588. 10.2307/2291069
Jordan MI: Hierarchical models, nested models and completely random measures. In Frontiers of Statistical Decision Making and Bayesian Analysis. Edited by: Chen M-H, Dey D, Mueller P, Sun D, Ye K. Springer, New York, NY, USA; 2010.
Acknowledgments
The work reported in this paper was funded in part by the UK Engineering and Physical Sciences Research Council, and in part by the Electro-Magnetic Remote Sensing (EMRS) Defence Technology Centre, established by the UK Ministry of Defence and run by a consortium of SELEX Sensors and Airborne Systems (now SELEX Galileo), Thales Defence, Roke Manor Research and Filtronic.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wallace EURASIP Member, A.M., Ye EURASIP Member, J., Krichel, N.J. et al. Full Waveform Analysis for Long-Range 3D Imaging Laser Radar. EURASIP J. Adv. Signal Process. 2010, 896708 (2010). https://doi.org/10.1155/2010/896708
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/896708



 .
.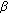 .
.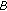 .
.





