- Research Article
- Open access
- Published:
Cyclic Biaxial Stress Measurement Method Using the Grain Growth Direction in Electrodeposited Copper Foil
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 928216 (2010)
Abstract
A method that uses grain growth direction in electrodeposited copper foil to measure cyclic biaxial stress is examined in this paper. The grain growth direction is measured by image processing software after a cyclic loading test for various biaxial stress ratios is carried out. Since the grain growth occurs in two directions and its directions correspond closely with the direction of maximum shearing stress when the biaxial stress ratio is negative, the principal stress can be measured using Mohr's stress circle. On the other hand, when the biaxial stress ratio is positive, above-mentioned feature does not occur. Therefore, the first principal stress can be measured based on the grain growth density. The number of grains necessary to measure the biaxial stress is estimated by a statistical approach.
1. Introduction
The copper electroplating method is used to measure cyclic stress that causes metal fatigue [1–3]. If copper foil adhered to a machine element is subjected to repeated loads, grain growth occurs in the copper foil. Since the grain growth density is controlled by the maximum shearing stress and the number of cycles, the maximum shearing stress can be measured based on the grain growth density in the prescribed number of cycles [4]. This method has the advantage of detecting stress in microscopic regions like the stress concentration region. Moreover, this method can be easily applied to rotating machines and machine elements in sealed casings, since it does not need an output line like an electrical resistance strain gauge.
Since the principal stresses that are important for evaluating metal fatigue cannot be detected by this method, a new method using copper foil with circular holes has been developed [4, 5]. However, this new method is somewhat complex, because the grain growth length at hole edges as well as the grain growth density in the copper foil must be measured. This also means that two kinds of copper foils (foil with and without circular holes) are necessary for the principal stress measurement.
From the above viewpoint, we examined the principal stress measurement using only one piece of foil without circular holes. To do this, we focused on the grain growth direction, since the growth direction of an individual grain is expected to correspond closely with the direction of maximum shearing stress. The principal stress measurement becomes possible using this feature as described in the next chapter. First, we proposed the principal stress measurement method based on the grain growth direction. Second, we investigated the relative frequency distribution of the grain growth direction for various biaxial stress conditions. Finally, the number of grains necessary to measure the principal stress was estimated by regarding the relative frequency distribution as the normal distribution.
2. Biaxial Stress Measurement Method
Figure 1 shows the stress state of the copper foil depicted by Mohr's stress circle. Namely, Figures 1(a) and 1(b) show conditions when the biaxial stress ratio  (= the second principal stress
(= the second principal stress  /the first principal stress
/the first principal stress  ) is negative and positive, respectively. Since there is usually no vertical load to the surface of machine element, the principal stress
) is negative and positive, respectively. Since there is usually no vertical load to the surface of machine element, the principal stress  perpendicular to this surface is zero. If the copper foil is adhered to this surface, the third principal stress in the foil
perpendicular to this surface is zero. If the copper foil is adhered to this surface, the third principal stress in the foil  is also zero, since the foil is very thin. Therefore, the principal stresses
is also zero, since the foil is very thin. Therefore, the principal stresses  and
and  are expressed as the following equation using the maximum shearing stress
are expressed as the following equation using the maximum shearing stress  and the biaxial stress ratio
and the biaxial stress ratio  :
:


We focus on the first principal stress  because it is the most important in metal fatigue evaluation. Since the maximum shearing stress
because it is the most important in metal fatigue evaluation. Since the maximum shearing stress  can be measured by the conventional method based on the grain growth density in the copper foil, the first principal stress
can be measured by the conventional method based on the grain growth density in the copper foil, the first principal stress  can be obtained easily when
can be obtained easily when  . However, it is necessary to measure the biaxial stress ratio C in addition to
. However, it is necessary to measure the biaxial stress ratio C in addition to  in the case of
in the case of  . Namely, determining the sign of biaxial stress ratio is required to measure the first principal stress, since the basic equation to obtain the first principal stress is different. Figure 2 illustrates grain growth in copper. The grain growth caused by cyclic stress in copper is considered to be a kind of thermal recrystallization [6]. The dislocation movement caused by mechanical rather than thermal energy results in the grain growth. Since the shearing stress is responsible for the dislocation movement, the grain growth is considered to be controlled by the shearing stress.
. Namely, determining the sign of biaxial stress ratio is required to measure the first principal stress, since the basic equation to obtain the first principal stress is different. Figure 2 illustrates grain growth in copper. The grain growth caused by cyclic stress in copper is considered to be a kind of thermal recrystallization [6]. The dislocation movement caused by mechanical rather than thermal energy results in the grain growth. Since the shearing stress is responsible for the dislocation movement, the grain growth is considered to be controlled by the shearing stress.  occurs in the direction that divides the
occurs in the direction that divides the  and
and  directions in two when
directions in two when  as shown in Figure 1(a). Therefore, the plane in which the shearing stress becomes the maximum is an
as shown in Figure 1(a). Therefore, the plane in which the shearing stress becomes the maximum is an  -plane, as shown in Figure 2(a). On the other hand,
-plane, as shown in Figure 2(a). On the other hand,  occurs in the direction that divides the
occurs in the direction that divides the  and
and  directions in two when
directions in two when  as shown in Figure 1(b). So, the plane in which the shearing stress becomes the maximum is an
as shown in Figure 1(b). So, the plane in which the shearing stress becomes the maximum is an  -plane, as shown in Figure 2(b). In addition, there are two directions where the shearing stress reaches the maximum, and the interval between the two is 9
-plane, as shown in Figure 2(b). In addition, there are two directions where the shearing stress reaches the maximum, and the interval between the two is 9 , as understood from Mohr's stress circle shown in Figure 1. As a result, the grain growth observed by electrochemical polishing occurred in the two directions and the interval between the two is 9
, as understood from Mohr's stress circle shown in Figure 1. As a result, the grain growth observed by electrochemical polishing occurred in the two directions and the interval between the two is 9 when
when  . On the other hand, the grains do not show the above-mentioned features on the
. On the other hand, the grains do not show the above-mentioned features on the  -plane when
-plane when  , since grains grow in the thickness direction. Therefore, the sign of biaxial stress ratio can be determined by using these characteristics.
, since grains grow in the thickness direction. Therefore, the sign of biaxial stress ratio can be determined by using these characteristics.
If the sign of biaxial stress ratio is determined,  can be obtained easily when
can be obtained easily when  using (2). Since the biaxial stress ratio
using (2). Since the biaxial stress ratio  becomes negative in the combined stress state of bending and torsion that exists widely in actual machine elements, the principal stress measurement under this condition is important. From (1), the measurement of biaxial stress ratio is necessary in this condition. Therefore, the method using copper foil with circular holes has been developed to measure biaxial stress ratio
becomes negative in the combined stress state of bending and torsion that exists widely in actual machine elements, the principal stress measurement under this condition is important. From (1), the measurement of biaxial stress ratio is necessary in this condition. Therefore, the method using copper foil with circular holes has been developed to measure biaxial stress ratio  [4, 5]. A new method using grain growth direction is examined to measure the principal stress using only a copper foil without circular holes. Figure 3 shows a machine element that receives bending moment
[4, 5]. A new method using grain growth direction is examined to measure the principal stress using only a copper foil without circular holes. Figure 3 shows a machine element that receives bending moment  and torsional moment
and torsional moment  at both longitudinal ends. The stress state of a small element is in the combined stress state of a bending stress σ
x
and a shearing stress
at both longitudinal ends. The stress state of a small element is in the combined stress state of a bending stress σ
x
and a shearing stress  as shown in Figure 3. Mohr's stress circle of this small element is shown in Figure 4. Since the first principal stress and the second principal stress have opposite signs, the biaxial stress ratio becomes negative. The angle
as shown in Figure 3. Mohr's stress circle of this small element is shown in Figure 4. Since the first principal stress and the second principal stress have opposite signs, the biaxial stress ratio becomes negative. The angle  between the axial direction and the direction of principal stress is expressed as
between the axial direction and the direction of principal stress is expressed as

Moreover, the relationship between the direction of principal stress  and the direction of maximum shearing stress
and the direction of maximum shearing stress  is expressed as
is expressed as

Since the growth direction of individual grains can be expected to correspond with  , the biaxial stress ratio
, the biaxial stress ratio  can be obtained from (3) and (4) when
can be obtained from (3) and (4) when  is measured by using the grain growth direction. Then, the principal stress can be measured from (1). Since this new method uses only one piece of foil, the principal stress can be measured more easily than with the conventional method.
is measured by using the grain growth direction. Then, the principal stress can be measured from (1). Since this new method uses only one piece of foil, the principal stress can be measured more easily than with the conventional method.
3. Experimental Procedures
3.1. Test Specimen and Testing Machine
A copper foil was obtained as follows. A stainless steel plate (200 mm  100 mm
100 mm  1 mm) was electroplated with copper sulfate solution [1]. Since the stainless steel plate is polished by buffing before plating, the deposited layer can easily strip from the stainless steel plate. This deposited layer is called a copper foil. All subsequent experiments were carried out by cutting this single foil to small pieces. The copper foil was about 20
1 mm) was electroplated with copper sulfate solution [1]. Since the stainless steel plate is polished by buffing before plating, the deposited layer can easily strip from the stainless steel plate. This deposited layer is called a copper foil. All subsequent experiments were carried out by cutting this single foil to small pieces. The copper foil was about 20  m thick and the initial grain size was about 1
m thick and the initial grain size was about 1  m [4]. This grain size is considerably smaller than the grown grain size.
m [4]. This grain size is considerably smaller than the grown grain size.
A titanium alloy (Ti-6Al-4V) was used as the specimen material. The mechanical properties are shown in Table 1. Figure 5 shows the geometry and dimensions of test specimen. A plate-type specimen was used for  , and a disk-type specimen was used for
, and a disk-type specimen was used for  . A Schenck type fatigue testing machine was used, and tests were performed at a frequency of 60 Hz by mounting the bending-torsion apparatus shown in Figure 6 in the test machine when
. A Schenck type fatigue testing machine was used, and tests were performed at a frequency of 60 Hz by mounting the bending-torsion apparatus shown in Figure 6 in the test machine when  . This apparatus is able to produce various biaxial stress ratios by changing the attachment angle
. This apparatus is able to produce various biaxial stress ratios by changing the attachment angle  . Table 2 shows the relationship between the biaxial stress ratio
. Table 2 shows the relationship between the biaxial stress ratio  and the attachment angle
and the attachment angle  obtained by a strain gauge rosette. On the other hand, the closed-loop servohydraulic testing machine was used, and tests were carried out at the same frequency by mounting the disk-bending apparatus shown in Figure 7 in the test machine when
obtained by a strain gauge rosette. On the other hand, the closed-loop servohydraulic testing machine was used, and tests were carried out at the same frequency by mounting the disk-bending apparatus shown in Figure 7 in the test machine when  . If the punch that has convex shape with a large curvature compresses the opposite side of the specimen surface where copper foil is adhered, the biaxial stress ratio of a copper foil becomes positive [7]. Since the stress state is different with the location on the disk, the copper foil is adhered to the central portion. The biaxial stress ratio C measured by a strain gauge rosette was 1.0. Images of grown grains were captured using a personal computer from a digital camera installed on an optical microscope (200x magnification), and we used image processing software to measure the grain growth direction.
. If the punch that has convex shape with a large curvature compresses the opposite side of the specimen surface where copper foil is adhered, the biaxial stress ratio of a copper foil becomes positive [7]. Since the stress state is different with the location on the disk, the copper foil is adhered to the central portion. The biaxial stress ratio C measured by a strain gauge rosette was 1.0. Images of grown grains were captured using a personal computer from a digital camera installed on an optical microscope (200x magnification), and we used image processing software to measure the grain growth direction.
3.2. Experimental Procedure
A piece of copper foil was adhered to the central portion of a specimen using cyano-acrylate-based strain gauge cement. After the specimen was installed in the apparatus, cyclic loading tests were carried out under  MPa. The image was captured as the longitudinal direction of the plate-type specimen was corresponding to the horizontal direction of the image. On the other hand, arbitrary direction of the disk-type specimen was chosen as the horizontal direction of the image. The growth direction
MPa. The image was captured as the longitudinal direction of the plate-type specimen was corresponding to the horizontal direction of the image. On the other hand, arbitrary direction of the disk-type specimen was chosen as the horizontal direction of the image. The growth direction  of individual grains was measured after electrochemically polishing and etching.
of individual grains was measured after electrochemically polishing and etching.  was defined as the angle between the horizontal direction of the image and the principal axis of the grown grain (the axis along which a moment of inertia of area is minimized), as shown in Figure 8(b). Namely,
was defined as the angle between the horizontal direction of the image and the principal axis of the grown grain (the axis along which a moment of inertia of area is minimized), as shown in Figure 8(b). Namely,  is expressed as
is expressed as

 ,
,  , and
, and  are the moment of inertia of area for the
are the moment of inertia of area for the  axis, the moment of inertia of area for the
axis, the moment of inertia of area for the  axis, and the product of inertia of area, respectively. Image processing software can automatically calculate the grain growth direction based on (5) using a binary image of the grown grains. The calculation was carried out for grains that did not coalesce with each other.
axis, and the product of inertia of area, respectively. Image processing software can automatically calculate the grain growth direction based on (5) using a binary image of the grown grains. The calculation was carried out for grains that did not coalesce with each other.
4. Results and Discussion
4.1. Statistical Distribution of the Grain Growth Direction
Figure 8 is a microphotograph of three examples of grain growth due to the cyclic stress. The direction of maximum shearing stress is also shown in the figure when  . As predicted, most grains grew in two directions of the maximum shearing stress and the interval between the two is 9
. As predicted, most grains grew in two directions of the maximum shearing stress and the interval between the two is 9 in the case of
in the case of  . On the other hand, these features are not recognized in the case of
. On the other hand, these features are not recognized in the case of  . Figure 9 shows some examples of the relative frequency distribution of grain growth direction
. Figure 9 shows some examples of the relative frequency distribution of grain growth direction  . In these figures,
. In these figures,  means the number of samples. The maximum shearing stress directions
means the number of samples. The maximum shearing stress directions  obtained by substituting the values of Table 2 for (3) and (4) are also shown in Figures 9(a) and 9(b). When
obtained by substituting the values of Table 2 for (3) and (4) are also shown in Figures 9(a) and 9(b). When  , peaks of the distribution correspond well with the direction of maximum shearing stress
, peaks of the distribution correspond well with the direction of maximum shearing stress  and the interval from one peak to the next peak is almost 9
and the interval from one peak to the next peak is almost 9 . These tendencies occurred for all experimental conditions in
. These tendencies occurred for all experimental conditions in  . However, these tendencies are not recognized in the case of
. However, these tendencies are not recognized in the case of  . From these results, it can be concluded that grain growth occurs readily in the direction of the maximum shearing stress.
. From these results, it can be concluded that grain growth occurs readily in the direction of the maximum shearing stress.
4.2. Biaxial Stress Measurement Using the Grain Growth Direction
The following periodic function is applied to approximate the relative frequency distribution, since the peaks occur periodically when  :
:

where  is the relative frequency of
is the relative frequency of  ,
,  is a constant that relates to the height of the peak (amplitude),
is a constant that relates to the height of the peak (amplitude),  is a constant that expresses the interval of a peak (period),
is a constant that expresses the interval of a peak (period),  is a constant that denotes a phase at
is a constant that denotes a phase at  (initial phase), and
(initial phase), and  is a constant that expresses the translation amount of upward direction. The values of each constant are listed in Table 3. The sin curve in Figure 9 graphs (6). The approximation curve corresponds well with the experimental results when
is a constant that expresses the translation amount of upward direction. The values of each constant are listed in Table 3. The sin curve in Figure 9 graphs (6). The approximation curve corresponds well with the experimental results when  .
.  are almost 9
are almost 9 in the case of
in the case of  from Table 3. Moreover, since the grains are clearly grown in the
from Table 3. Moreover, since the grains are clearly grown in the  -plane as shown in Figure 2(a),
-plane as shown in Figure 2(a),  are large values compared with the case of
are large values compared with the case of  . Therefore, the sign of biaxial stress ratio can be decided by using these parameters. Namely, we first pay attention to the
. Therefore, the sign of biaxial stress ratio can be decided by using these parameters. Namely, we first pay attention to the  value. If this value is almost 9
value. If this value is almost 9 , biaxial stress ratio is probably negative. However, the
, biaxial stress ratio is probably negative. However, the  value might be about 9
value might be about 9 even when
even when  as a result of the approximation. Therefore, we next check the
as a result of the approximation. Therefore, we next check the  value. If this is the large value as shown in Table 3 (
value. If this is the large value as shown in Table 3 ( ), it can be concluded that the biaxial stress ratio is negative. If not so, the biaxial stress ratio is positive.
), it can be concluded that the biaxial stress ratio is negative. If not so, the biaxial stress ratio is positive.
Next, we discuss the measurement of biaxial stress ratio when  . Since the approximated equation (6) corresponds well with the experimental results, the peak value of
. Since the approximated equation (6) corresponds well with the experimental results, the peak value of  can be obtained by differentiating this equation, and the resultant equation is
can be obtained by differentiating this equation, and the resultant equation is

Figure 10 shows  obtained by the above equation in each biaxial stress ratio
obtained by the above equation in each biaxial stress ratio  and the theoretical curve of
and the theoretical curve of  obtained by substituting (3) for (4). In this figure,
obtained by substituting (3) for (4). In this figure,  is obtained from the approximation curve at
is obtained from the approximation curve at  .
.  obtained by the new method using grain growth direction agrees well with a theoretical curve of
obtained by the new method using grain growth direction agrees well with a theoretical curve of  . Therefore, it is possible to measure biaxial stress ratio
. Therefore, it is possible to measure biaxial stress ratio  when
when  by substituting
by substituting  for
for  in (4) and using (3). Since the maximum shearing stress
in (4) and using (3). Since the maximum shearing stress  can be measured by the conventional method based on the grain growth density in a microscopic region, the principal stress can be obtained by (1).
can be measured by the conventional method based on the grain growth density in a microscopic region, the principal stress can be obtained by (1).
4.3. Estimation of the Number of Grains Necessary to Measure the Biaxial Stress
Since this method has the advantage of enabling measurements of the stress in a microscopic region, it is preferable to reduce the number of measured grains  as much as possible. The number of grains necessary to determine the sign of biaxial stress ratio is only about 50, since the feature shown in Figure 9 is the same within the range from 50 to 150. Therefore, we pay attention to the number of grains
as much as possible. The number of grains necessary to determine the sign of biaxial stress ratio is only about 50, since the feature shown in Figure 9 is the same within the range from 50 to 150. Therefore, we pay attention to the number of grains  necessary to measure the biaxial stress ratio. Namely,
necessary to measure the biaxial stress ratio. Namely,  necessary to keep prescribed accuracy in the stress measurement can be statistically estimated.
necessary to keep prescribed accuracy in the stress measurement can be statistically estimated.
It is thought that the distribution shown in Figures 9(a) and 9(b) consists of two groups, since there are two directions of maximum shearing stress in an  -plane. Therefore, data within the range of
-plane. Therefore, data within the range of  4
4 from one peak of the distribution can be assumed to be one group. The cumulative relative frequency from one group in Figures 9(a) and 9(b) is plotted on normal probability paper and shown in Figure 11. Since most data can be plotted as straight lines for each biaxial stress ratio, the grain growth direction of one group can be considered to be the normal distribution expressed by the following probability density function
from one peak of the distribution can be assumed to be one group. The cumulative relative frequency from one group in Figures 9(a) and 9(b) is plotted on normal probability paper and shown in Figure 11. Since most data can be plotted as straight lines for each biaxial stress ratio, the grain growth direction of one group can be considered to be the normal distribution expressed by the following probability density function  :
:

where  is the population mean and
is the population mean and  is the population variance. When
is the population variance. When  samples are extracted from a population with a normal distribution, the distribution of the average of the
samples are extracted from a population with a normal distribution, the distribution of the average of the  samples
samples  also becomes a normal distribution, and the standard deviation of
also becomes a normal distribution, and the standard deviation of  samples becomes
samples becomes  [8]. Therefore, when the error margin
[8]. Therefore, when the error margin  % is permitted to be
% is permitted to be  based on
based on  , the probability that
, the probability that  is in the range of
is in the range of  can be calculated statistically [9]. Table 4 shows the values of
can be calculated statistically [9]. Table 4 shows the values of  obtained for various
obtained for various  , and Figure 12 shows the first principal stress
, and Figure 12 shows the first principal stress  obtained by substituting the mean value
obtained by substituting the mean value  calculated by extracting
calculated by extracting  samples shown in Table 4 for
samples shown in Table 4 for  in (4). The error range of
in (4). The error range of  obtained from
obtained from  is also shown in the figure. Moreover, the solid curve in the figure shows the theoretical curve obtained by substituting
is also shown in the figure. Moreover, the solid curve in the figure shows the theoretical curve obtained by substituting  MPa to (1). The first principal stress
MPa to (1). The first principal stress  calculated by using
calculated by using  samples was in the specified error range. Moreover,
samples was in the specified error range. Moreover,  obtained by the new method agrees well with the theoretical curve. The area necessary for the principal stress measurement is only about 5 mm2, even when a condition requires many samples (
obtained by the new method agrees well with the theoretical curve. The area necessary for the principal stress measurement is only about 5 mm2, even when a condition requires many samples ( ,
,  %). Therefore, this new method can detect the cyclic biaxial stress in a small area using only one piece of copper foil.
%). Therefore, this new method can detect the cyclic biaxial stress in a small area using only one piece of copper foil.
 (Confidence value: 95%).
(Confidence value: 95%).5. Conclusions
We examined a method that uses the growth direction of grains in copper foil to measure cyclic biaxial stress. The number of grains necessary to measure the biaxial stress was also estimated statistically.
The results obtained are summarized as follows.
-
(1)
When the biaxial stress ratio is negative, peaks of the relative frequency distribution of the grain growth direction corresponded well with the direction of maximum shearing stress, and the interval from one peak to another peak was almost 9
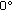 .
. -
(2)
The above-mentioned features are not recognized when the biaxial stress ratio is positive. Therefore, the sign of biaxial stress ratio is determined by using these features.
-
(3)
The principal stress was obtained with Mohr's stress circle and the peak of the sin curve obtained by approximating the relative frequency distribution when the biaxial stress ratio is negative.
-
(4)
The grain growth direction within the range of
 4
4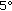 from one peak of the distribution followed the normal distribution. Therefore, the number of grains necessary for the principal stress measurement could be estimated to the demanded accuracy.
from one peak of the distribution followed the normal distribution. Therefore, the number of grains necessary for the principal stress measurement could be estimated to the demanded accuracy. -
(5)
The first principal stress
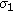 obtained by this new method agreed well with the result obtained by a strain gauge rosette. The area necessary for the principal stress measurement was only 5 mm2.
obtained by this new method agreed well with the result obtained by a strain gauge rosette. The area necessary for the principal stress measurement was only 5 mm2. -
(6)
Since this method can measure the principal stress with only one piece of foil, it is more efficient than conventional methods.
References
Ohkubo H: Copper electroplating method of stress analysis. Memoirs of the School of Engineering Nagoya University 1968, 20-21: 1.
Kato A, Mizuno T: Stress concentration factors of grooved shaft in torsion. Journal of Strain Analysis for Engineering Design 1985, 20(3):173-177. 10.1243/03093247V203173
Nagase Y, Yoshizaki T: Fatigue gage utilizing slip-initiation phenomenon in electroplated copper foil. Experimental Mechanics 1993, 33(1):49-54. 10.1007/BF02322550
Kitaoka S, Ono Y: Cyclic biaxial stress measurement by electrodeposited copper foil with circular holes. Strain 2006, 42: 49-56. 10.1111/j.1475-1305.2006.00249.x
Kitaoka S, Chen J-Q, Egami N, Hasegawa J: Measurement of biaxial stress using electrodeposited copper foil with a microcircular hole. JSME International Journal, Series A 1996, 39(4):533-539.
Kato A: Stress measurement by copper electroplating aided by a personal computer. Experimental Mechanics 1987, 27(2):132-137. 10.1007/BF02319464
Timoshenko S, Woinowsky-krieger S: Theory of Plates and Shells. 2nd edition. McGraw-Hill, New York, NY, USA; 1959.
Montgomery DC, Runger GC: Applied Statistics and Probability for Engineers. 3rd edition. John Wiley & Sons, New York, NY, USA; 2003.
Montgomery DC, Runger GC: Applied Statistics and Probability for Engineers. 4th edition. John Wiley & Sons, New York, NY, USA; 2003.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ono, Y., Li, C. & Hino, D. Cyclic Biaxial Stress Measurement Method Using the Grain Growth Direction in Electrodeposited Copper Foil. EURASIP J. Adv. Signal Process. 2010, 928216 (2010). https://doi.org/10.1155/2010/928216
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/928216






 ).
).
 )(b) Disk-type (
)(b) Disk-type ( )
)






 .
.



 (
( ) and
) and  .
.

 and
and  (
( %).
%).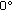 .
. 4
4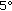 from one peak of the distribution followed the normal distribution. Therefore, the number of grains necessary for the principal stress measurement could be estimated to the demanded accuracy.
from one peak of the distribution followed the normal distribution. Therefore, the number of grains necessary for the principal stress measurement could be estimated to the demanded accuracy.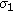 obtained by this new method agreed well with the result obtained by a strain gauge rosette. The area necessary for the principal stress measurement was only 5 mm2.
obtained by this new method agreed well with the result obtained by a strain gauge rosette. The area necessary for the principal stress measurement was only 5 mm2.