- Research Article
- Open access
- Published:
Techniques for Effective Optical Noise Rejection in Amplitude-Modulated Laser Optical Radars for Underwater Three-Dimensional Imaging
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 958360 (2010)
Abstract
Amplitude-modulated (AM) laser imaging is a promising technology for the production of accurate three-dimensional (3D) images of submerged scenes. The main challenge is that radiation scattered off water gives rise to a disturbing signal (optical noise) that degrades more and more the quality of 3D images for increasing turbidity. In this paper, we summarize a series of theoretical findings, that provide valuable hints for the development of experimental methods enabling a partial rejection of optical noise in underwater imaging systems. In order to assess the effectiveness of these methods, which range from modulation/demodulation to polarimetry, we carried out a series of experiments by using the laboratory prototype of an AM 3D imager ( = 405 nm) for marine archaeology surveys, in course of realization at the ENEA Artificial Vision Laboratory (Frascati, Rome). The obtained results confirm the validity of the proposed methods for optical noise rejection.
= 405 nm) for marine archaeology surveys, in course of realization at the ENEA Artificial Vision Laboratory (Frascati, Rome). The obtained results confirm the validity of the proposed methods for optical noise rejection.
1. Introduction
The growing interest for underwater 3D imaging, with applications ranging from the monitoring of submarine archaeological sites to the inspection of submerged structures for industrial and scientific purposes, has stimulated in recent years the development of 3D optical imagers specifically designed to operate underwater [1].
A promising category of underwater 3D imagers is represented by continuous-wave amplitude-modulated laser optical radars [2, 3], whose overland counterparts can achieve—in air—a line-of-sight accuracy of hundreds of micrometers at tens of meters of distance. These systems belong to the class of incoherent rangefinders. Distance  is determined indirectly through the measurement of the phase difference
is determined indirectly through the measurement of the phase difference  between the modulated intensity of a laser beam-used as the carrier of a radio-frequency modulating signal- and a reference signal:
between the modulated intensity of a laser beam-used as the carrier of a radio-frequency modulating signal- and a reference signal:

where  is the light speed in the medium and
is the light speed in the medium and  the modulation frequency.
the modulation frequency.
The uncertainty  in distance measurements, in regime of shot noise dominance, can be estimated by means of the formula
in distance measurements, in regime of shot noise dominance, can be estimated by means of the formula

where  is the modulation depth and
is the modulation depth and  the current signal-to-noise ratio, depending, among others, on the received power and measurement integration time.
the current signal-to-noise ratio, depending, among others, on the received power and measurement integration time.
The advantage of this approach is that it requires continuous-wave, low power laser light, making it possible to realize more robust, affordable and non-invasive devices. It also natively enables one to acquire, in a single scan, self-registered range—that is, geometric- and reflectivity/color—that is, imaging-information. All pieces of information, recorded in the form of two-dimensional arrays of structured data, are then integrated and transformed into 3D images by means of dedicated software. These features make AM laser optical radars particularly well suited for applications in the field of cultural heritage cataloguing and conservation, where they are widely used for the 3D digitization of both single artworks (paintings, sculptures, pottery) and entire sceneries (façades and interiors of historical buildings, archaeological sites).
While AM rangefinding in air is nowadays a mature technology, the development of underwater AM optical radars is still an important scientific and technological challenge, which poses several problems in terms of reliability and attainable accuracy. This is mainly due to the non-cooperative nature of water, a much more absorbing and scattering medium than air.
The intensity  of a light beam propagating through water is attenuated because of absorption and scattering events due to dissolved molecules and suspended particles. In the regime of single scattering dominance, the rate of attenuation is well described by the Lambert-Beer law, which for a homogenous medium of thickness z is written as
of a light beam propagating through water is attenuated because of absorption and scattering events due to dissolved molecules and suspended particles. In the regime of single scattering dominance, the rate of attenuation is well described by the Lambert-Beer law, which for a homogenous medium of thickness z is written as

Here  is the intensity of transmitted radiation and
is the intensity of transmitted radiation and  the total attenuation coefficient. The latter—which depends in general on the radiation wavelength as well as, for inhomogeneous media, on space coordinates—accommodates for intensity losses due to both absorption and scattering, and can be expressed as
the total attenuation coefficient. The latter—which depends in general on the radiation wavelength as well as, for inhomogeneous media, on space coordinates—accommodates for intensity losses due to both absorption and scattering, and can be expressed as  , where
, where  and
and  denote the absorption and scattering coefficients, respectively.
denote the absorption and scattering coefficients, respectively.
In underwater laser imaging applications, the effect of light absorption can in principle be reduced by properly selecting the laser wavelength in the region where transmission has a maximum. For pure water, light absorption is minimal in the blue-green region of the visible spectrum ( ) [4, 5]. In particular, the use of green laser light permits to reduce absorption for turbid water with a relatively abundant chlorophyll concentration, typical of coastal seawater. In the case of interest for the present work-open sea characterized by rather clean seawater-the minimum of absorption is better matched by using laser light in the violet-blue region of the visible spectrum (
) [4, 5]. In particular, the use of green laser light permits to reduce absorption for turbid water with a relatively abundant chlorophyll concentration, typical of coastal seawater. In the case of interest for the present work-open sea characterized by rather clean seawater-the minimum of absorption is better matched by using laser light in the violet-blue region of the visible spectrum ( ).
).
The other phenomenon affecting the performances of underwater laser imagers is scattering. Light backscattered by water and falling into the angular field of view of the receiver gives rise to an undesirable signal (optical noise), which combines with the target signal that carries the information necessary to image reconstruction. (Because of its deleterious effects on 3D imaging measures, the signal due to light backscattered by water is often referred to as optical noise in this work-although it cannot be considered noise in strict sense.) The result is a reduction of the accuracy of range measurements, as well as a degradation of image contrast. It follows that optical noise has to be strongly reduced, in order to obtain 3D images of high contrast, resolution and accuracy.
A partial reduction can be achieved by means of a bistatic optical layout, that is, by increasing the spatial separation between the launching and receiving stages [6]. The main drawback of this method is that it does not guarantee an effective filtering of the radiation backscattered by the initial part of the water column, which otherwise provides the most important contribution to the total noise. So, most effective rejection methods are necessary.
In this article, we present the results of research recently carried out in the ENEA Artificial Vision Laboratory (Frascati, Rome, Italy) on scattered light rejection using modulation/demodulation and polarization techniques. The Artificial Vision Laboratory comprises researchers with a long-dating experience in the development of both coherent and incoherent optoelectronic devices, and dedicated software for artificial vision applications. The line of research on optical noise rejection is specifically targeted at the realization of a new underwater 3D imager, the AM Underwater Laser Optical Radar (AMULOR), which is at the moment of writing in course of advanced development. The first AMULOR operational system will be released in late 2009 as a deliverable of the BLU-Archeosys national project, funded by the Italian Ministry for University and Research. The final system will be mounted on a remotely operated vehicle and used for the survey of submerged archaeological sites at depths of a few tenths of meters, so in conditions of rather clear seawater.
As a preparatory step to the realization of the AMULOR 3D imager, an experimental test bed has been set up in the ENEA Frascati research center, comprising a couple of tanks (1.56 m and 25 m long, resp.) equipped with an antireflection coated entrance window, and a laboratory prototype of the imager itself, supplemented, in case, by a polarization-sensitive receiving stage.
The test bed was used to carry out various series of measurements in conditions of clean and relatively turbid water, obtained by adding proper amounts of a diffusing element—such as skim milk and Maalox —to tap water. Different scattering regimes (Rayleigh, intermediate or quasi-Mie) were explored, mainly in the limit of optically thin medium, where single scattering prevails on multiple scattering and polarization memory effects are negligible. The results of these experiments, reported in the present work, provided useful insights for the design and optimal configuration of the AMULOR.
—to tap water. Different scattering regimes (Rayleigh, intermediate or quasi-Mie) were explored, mainly in the limit of optically thin medium, where single scattering prevails on multiple scattering and polarization memory effects are negligible. The results of these experiments, reported in the present work, provided useful insights for the design and optimal configuration of the AMULOR.
The paper is organized as follows. In the first part, we set up a simple theoretical framework, by summarizing results that help shed light on the characteristics of optical noise in underwater imaging systems. In particular, in Sections 2 and 3 we develop a simplified model of water backscattering that specifically applies to the case of AM laser imagers, by providing an analytical solution to the corresponding radiative transfer problem in the small angle diffusion approximation. The model is exploited in Section 4 to outline some possible modulation/demodulation experimental procedures, that enable the cancellation of optical noise by exploiting the existence of an interference-like effect between water and target signals. A complementary polarimetric approach is described in Section 5, where we briefly introduce the Muller-Stokes formalism, and use it to give grounds for the different polarization characteristics of light scattered by the medium and the target, respectively. In the second part of the article, we assess the effectiveness of the optical noise rejection techniques suggested by theory, by describing a number of experiments purposely carried out in the ENEA laboratories. Specifically, the experimental apparatus is briefly described in Section 6. In Section 7 we verify the low-pass filter behavior of water backscattering as a function of the modulation frequency in AM systems [7–9]. The analysis of how the water backscattering signal affects the performance of AM laser 3D imagers in turbid water—firstly published in [10] and then further explored in [11, 12]—is given in Section 8, where methods for the direct cancellation of the optical noise are also suggested. Finally, in Section 9 results obtained by using a specific polarimetric technique [13] for optical noise reduction are presented and discussed, followed by conclusions and acknowledgments.
1.1. Part I Theory
We provide in the following a simplified theoretical description of the most relevant properties that characterize the optical noise revealed by 3D laser imagers. The treatment is aimed at emphasizing those aspects that can be utilized for the reduction of optical noise effects in real conditions.
In Sections 2 and 3 we derive a simple theoretical model, that incorporates the most important physical processes involved in the operation of a typical underwater AM laser 3D imager. The model permits to calculate, within the framework of the radiative transfer theory [14, 15] and in idealized yet still sufficiently realistic conditions, the power falling onto the system's receiver when an AM laser beam is shot in open water. This result is used, in Section 4, to predict the observation of an interference-like pattern in the signal detected by an underwater AM 3D imager.
The logical steps of the derivation are the following. Using the Multi-Component Approach (MCA) [14, 16, 17], the initial problem is firstly split into a system of Radiative Transfer Equations (RTEs), admitting a clearer physical interpretation in terms of forward and diffuse components. The Small Angle Approximation (SAA) is then used to simplify the equations [14, 18]. The SAA can be applied whenever the scattering probability strongly favors forward scattering events at small angles, that is, the phase function is strongly peaked in the forward direction. This condition is generally met by natural waters—such as seawater—where the angular deviation of light rays from their initial directions after a scattering event is usually very small and directed forwards. Finally, the Small Angle Diffusion Approximation (SADA) is applied [14, 17]. This enables a further simplification of the mathematical problem, which can then be explicitly solved. The resulting model takes into account single backscattering events, as well as the spread of the laser beam due to multiple scattering events in the forward direction at small angles.
In Section 5, finally, we use the Stokes-Muller formalism for demonstrating some important polarization properties of backscattered radiation, that permit to motivate the use of polarimetry as a means for optical noise rejection.
2. Optical Noise and Radiative Transfer Equation in Underwater AM Imagers
Consider a point-like, perfectly collimated, AM laser source located at the origin of a Cartesian system with coordinates  . Let the plane
. Let the plane  coincide with the separation interface between air (
coincide with the separation interface between air ( ) and water (
) and water ( ). The laser starts shooting at
). The laser starts shooting at  along the positive
along the positive  axis with power
axis with power

where  is the modulation frequency and
is the modulation frequency and  the modulation depth (
the modulation depth ( ).
).
A receiver, also located on the plane  , but centered around the point
, but centered around the point  at a distance
at a distance  from the origin, collects the radiation backscattered by the medium and falling onto the sensitive area
from the origin, collects the radiation backscattered by the medium and falling onto the sensitive area  and within the acceptance solid angle
and within the acceptance solid angle  . We aim at calculating the received power as a function of all intrinsic and extrinsic parameters of the imaging system, comprising light source, medium and receiver.
. We aim at calculating the received power as a function of all intrinsic and extrinsic parameters of the imaging system, comprising light source, medium and receiver.
It is convenient to model the imager's receiving stage with a function  , which represents the receiver's normalized spatial-angular sensitivity pattern to radiation falling at point
, which represents the receiver's normalized spatial-angular sensitivity pattern to radiation falling at point  in the direction identified by the versor
in the direction identified by the versor  . The received power is then given by
. The received power is then given by

where  is the radiance of the optical field (power per unit projected area and unit solid angle). Once a suitable sensitivity pattern is assumed for the receiver, the problem is thus reduced to the determination of the radiance
is the radiance of the optical field (power per unit projected area and unit solid angle). Once a suitable sensitivity pattern is assumed for the receiver, the problem is thus reduced to the determination of the radiance  , that is, to solving the following non-stationary, linear, integro-differential radiative transfer equation:
, that is, to solving the following non-stationary, linear, integro-differential radiative transfer equation:

(We neglect thermal emission as not particularly relevant for the problem considered in this article.)Here  is the speed of light in the medium, and
is the speed of light in the medium, and  is the attenuation coefficient (
is the attenuation coefficient ( and
and  are the absorption and scattering coefficients, respectively), which is constant all over the medium, supposed homogeneous.
are the absorption and scattering coefficients, respectively), which is constant all over the medium, supposed homogeneous.  represents the gradient operator and
represents the gradient operator and  is the scattering phase function, which we assume depending only on the scattering angle
is the scattering phase function, which we assume depending only on the scattering angle  (
( ) through
) through  . With the chosen conventions, the quantity
. With the chosen conventions, the quantity  is naturally interpreted as the probability density that radiation propagating along
is naturally interpreted as the probability density that radiation propagating along  is scattered in direction
is scattered in direction  . The last term in (6) is an external source term modeling the injected light, which in the case at hand can be written as
. The last term in (6) is an external source term modeling the injected light, which in the case at hand can be written as  .
.
Equation (6) represents the law of radiant energy conservation and provides an appropriate description of the interaction of light with matter as long as propagation distances are much larger than the wavelength. Analytical solutions to this equation can only be found in very specific cases, corresponding to well specified simplifying assumptions.
It is firstly convenient to reduce the non-stationary problem to a stationary one, by taking the Fourier transform with respect to time of (6):

(In order to simplify the notations, if not explicitly stated otherwise, we adopt the convention to distinguish functions and their Fourier transforms only from the list of arguments.) is eventually recovered from
is eventually recovered from  by taking the inverse transform:
by taking the inverse transform:

It is worth noticing that  appears in (7) only as a parameter. In order to keep notations simple, we are thus allowed to ignore the dependence on
appears in (7) only as a parameter. In order to keep notations simple, we are thus allowed to ignore the dependence on  initially, with the assumption to restate it at the end of the calculation. Thus, we are led to seek a solution to the following stationary RTE:
initially, with the assumption to restate it at the end of the calculation. Thus, we are led to seek a solution to the following stationary RTE:

The first step consists in applying the MCA, in order to distinguish between forward and diffuse radiation,  , by assuming that
, by assuming that

Here  , and
, and  and
and  are legitimate phase functions describing the scattering over small forward- and large backward angles, respectively. This enables one to rewrite (7) as
are legitimate phase functions describing the scattering over small forward- and large backward angles, respectively. This enables one to rewrite (7) as

where we have introduced the quantities  and
and  (
( ). The new source term
). The new source term  is completely determined after solving the first equation. The system of (11) is so far equivalent to (7). A first simplifying approximation can be made at this point by expanding
is completely determined after solving the first equation. The system of (11) is so far equivalent to (7). A first simplifying approximation can be made at this point by expanding  in powers of
in powers of  and only retaining terms of order
and only retaining terms of order  in the corresponding equation. This amounts to modifying the initial problem into a new one, where only single backscattering events are considered. No approximation is made in the equation for the forward component, which thus encompasses forward scattering at all orders. The new equations read
in the corresponding equation. This amounts to modifying the initial problem into a new one, where only single backscattering events are considered. No approximation is made in the equation for the forward component, which thus encompasses forward scattering at all orders. The new equations read

It is important to notice that both  and
and  obey now to the same RTE, yet with different source terms. If we manage to calculate the corresponding Green's function
obey now to the same RTE, yet with different source terms. If we manage to calculate the corresponding Green's function  , the forward and diffuse radiance components can be immediately recovered as
, the forward and diffuse radiance components can be immediately recovered as

where we substituted to  its definition in terms of
its definition in terms of  .
.
It is possible to derive an elegant, symmetric expression for the power falling onto the receiver by substituting the second of (13) into (5), and using the property

which is a direct consequence of the optical reciprocity theorem [14, 19]. After a few manipulations, one obtains

Here,  is given by the first of (13), while
is given by the first of (13), while  is obtained by the latter with the substitution
is obtained by the latter with the substitution  . The new quantity
. The new quantity  can be interpreted as a fictitious source with an emission spatial-angular pattern identical to the reception pattern of the receiver.
can be interpreted as a fictitious source with an emission spatial-angular pattern identical to the reception pattern of the receiver.
In order to find explicit expressions for  and
and  , and further simplify (15), we make the reasonable assumption that the underlying RTE-see (12)-admits a formulation in terms of the so-called small angle approximation. This amounts to assuming that the angles
, and further simplify (15), we make the reasonable assumption that the underlying RTE-see (12)-admits a formulation in terms of the so-called small angle approximation. This amounts to assuming that the angles  formed by forward scattered radiation with the incidence direction of the laser beam are very small, so that the following substitutions can be made:
formed by forward scattered radiation with the incidence direction of the laser beam are very small, so that the following substitutions can be made:

where  is the projection of
is the projection of  on the plane
on the plane  , with
, with  .
.
In this approximation, (15) can be eventually rewritten as

where  admits a natural interpretation as backward diffuse phase function and
admits a natural interpretation as backward diffuse phase function and

Each of the forward radiance functions entering (18) obeys a SAA radiative transfer equation of the form

Equation (19) can be solved analytically after applying 2D Fourier transforms in both  and
and  . Assuming that
. Assuming that  and
and  are the Fourier conjugates of
are the Fourier conjugates of  and
and  , respectively, the solution reads [18]
, respectively, the solution reads [18]

By substituting this result into the Fourier transform of (18), we get

where  is the Fourier transform of an effective source defined, in direct space, by the following combination of
is the Fourier transform of an effective source defined, in direct space, by the following combination of  and
and  :
:

Equation (21) is directly related to the solution of the following effective radiative transfer problem:

which is identical to (19), apart from the source term and the doubled values of the optical coefficients. In fact, using (20) to solve (23), it is easy to verify that

This result represents a particular derivation of the so-called equivalent medium theorem [19–21], valid in the small angle approximation, which states that the power backscattered by a medium is the same as that due to an equivalent effective medium, that has the same phase function as the true medium—but twice the extinction and scattering coefficients, that is,  and
and  —on the forward journey, and zero extinction and scattering coefficients on the return journey. So, also taking into due account the substitution
—on the forward journey, and zero extinction and scattering coefficients on the return journey. So, also taking into due account the substitution  , the two-way problem is transformed into a simpler equivalent one-way propagation problem.
, the two-way problem is transformed into a simpler equivalent one-way propagation problem.
In conclusion, the power falling onto the receiver can be written in terms of the effective forward radiance at  :
:

In most practical situations, the latter expression can be further simplified by posing  , that is
, that is  , where
, where  is the volume scattering function evaluated at backscattering. In this case, (25) becomes
is the volume scattering function evaluated at backscattering. In this case, (25) becomes

 is the effective forward irradiance along the
is the effective forward irradiance along the  axis, which is most easily calculated directly in terms of
axis, which is most easily calculated directly in terms of  by means of the formula
by means of the formula

In summary, in the limits of validity of the various approximation used, we can apply the following recipe to estimate the power backscattered by the medium and falling onto the receiver:
-
(1)
provide explicit expressions for
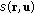 and
and 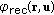 , and calculate
, and calculate (28)
(28) -
(2)
provide an explicit expression for
 , and calculate its Fourier transform
, and calculate its Fourier transform 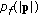 ;
; -
(3)
evaluate the integral
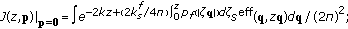 (29)
(29) -
(4)
estimate
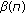 and eventually calculate
and eventually calculate (30)
(30)
Due to the complexity of the calculations, explicit results can only be obtained in specific cases. In the next section, we provide a general solution to the problem, based on the small angle diffusion approximation, that does not depend on an ansatz for  .
.
3. A Model for Optical Noise in the Small Angle Diffusion Approximation
The small angle diffusion approximation basically consists in modifying the small-angle integro—differential RTE, so as to turn it into a simpler partial differential equation, containing a new diffusion-like term—whence the name.
In fact, if the effective radiance is assumed to vary in  —that is, as a function of
—that is, as a function of  —much more slowly than
—much more slowly than  , then we can expand
, then we can expand  in Taylor's series in the integrand of (23), and only keep terms up to the second order in
in Taylor's series in the integrand of (23), and only keep terms up to the second order in  :
:

With this substitution, and using the fact that  is an even function of
is an even function of  and
and  , (23) becomes
, (23) becomes

where  is the so-called reduced attenuation coefficient,
is the so-called reduced attenuation coefficient,  is the Laplacian operator, and
is the Laplacian operator, and  plays the role of a diffusion coefficient. The quantity
plays the role of a diffusion coefficient. The quantity

represents the variance (second moment) of the forward phase function. The rest of the structure of the phase function is ignored in this approach. In more quantitative terms, it is possible to show that, in order for the SADA to be applicable, the condition  must hold [14, 17], where
must hold [14, 17], where  is the variance of the angular radiance distribution, corresponding to the mean square angular photon deviation from the beam axis.
is the variance of the angular radiance distribution, corresponding to the mean square angular photon deviation from the beam axis.
The solution of (32) can be obtained by using the same method applied to solve (19). In Fourier space, it reads

Using the recipe outlined in the previous section, the power falling onto the receiver can eventually be written in SADA as

with

In order to write an explicit formula for  as a function of all intrinsic and extrinsic parameters (optical constants, area and angular field of view of the receiver, etc.), we need to provide a suitable expression for
as a function of all intrinsic and extrinsic parameters (optical constants, area and angular field of view of the receiver, etc.), we need to provide a suitable expression for  , that is, ultimately, for the source
, that is, ultimately, for the source  and the receiver
and the receiver  .
.
The source term, modeling the injected laser light, can be conveniently written, in the case at hand, as

In order to simplify the calculations, we are here assuming in first approximation the laser beam as an ideal, fully collimated, geometric ray, corresponding to the limit case of a collimated Gaussian beam for infinitesimal beam size. More refined treatments, though possible, are beyond the scope of the present work.
It is convenient to assume for the receiver a Gaussian spatial-angular sensitivity pattern  , that is
, that is

By taking the Fourier transforms of (37) and (38), and substituting into (28), we eventually obtain


The Gaussian integral in (40) can easily be calculated, giving

where

Note that, by recalling the expression of  , and posing
, and posing  ,
,  —valid in the hypothesis of a very narrow receiver field of view semiangle
—valid in the hypothesis of a very narrow receiver field of view semiangle  —, (42) can also be written in the form
—, (42) can also be written in the form

In summary, the power backscattered by an infinite column of optically homogeneous water illuminated by a laser source with power  , and falling onto a narrow-field-of-view receiver of radius
, and falling onto a narrow-field-of-view receiver of radius  , located at a distance
, located at a distance  from the laser source, can be written in SADA as
from the laser source, can be written in SADA as

where the attenuation factor  is constant for fixed values of all the parameters.
is constant for fixed values of all the parameters.
We can reinstate the dependence on the frequency  by making the substitutions (We are here representing the incident power (see (4)) in complex notation as
by making the substitutions (We are here representing the incident power (see (4)) in complex notation as  , that is,
, that is,  , with the usual assumption that only the real part of the final result is eventually retained.)
, with the usual assumption that only the real part of the final result is eventually retained.)  , with
, with  , and
, and  . After taking the inverse Fourier transform with respect to
. After taking the inverse Fourier transform with respect to  (see (8)), we obtain
(see (8)), we obtain

where



Equation (45) represents an explicit solution of the original problem, obtained by taking into account only single backscattering—but multiple forward scattering-in the small angle diffusion approximation. According to this result, the oscillating part of the received power is characterized by an attenuation factor  and a phase shift
and a phase shift  that both depend on the modulation frequency (note that, obviously,
that both depend on the modulation frequency (note that, obviously,  ,
,  ). Unfortunately, the integral in (46) cannot be solved analytically if not for specific choices of the parameters. In all other cases, the integral must be evaluated numerically.
). Unfortunately, the integral in (46) cannot be solved analytically if not for specific choices of the parameters. In all other cases, the integral must be evaluated numerically.
Although not particularly realistic, it is instructive to consider the analytic expression of  obtained for
obtained for  —corresponding to a monostatic imager and an extremely forward-peaked phase function, respectively- and infinitesimal angle of acceptance (This condition can be imposed by initially setting
—corresponding to a monostatic imager and an extremely forward-peaked phase function, respectively- and infinitesimal angle of acceptance (This condition can be imposed by initially setting  which is the limit value of eq. (38) for very small
which is the limit value of eq. (38) for very small  ). In this case we get:
). In this case we get:

that is, the amplitude of the oscillating part of the received power has a low-pass filter dependence on the modulation frequency, with a cut-off frequency  coinciding with
coinciding with  . It is easy to verify, by numerically evaluating (47) for more physically significant values of the parameters, that the low-pass filter behavior is indeed a universal property of
. It is easy to verify, by numerically evaluating (47) for more physically significant values of the parameters, that the low-pass filter behavior is indeed a universal property of  , although the cut-off frequency does not in general coincide with
, although the cut-off frequency does not in general coincide with  , but rather depends in a complicated way on all—both intrinsic and extrinsic—parameters. Examples of this behavior will be given in Section 7.
, but rather depends in a complicated way on all—both intrinsic and extrinsic—parameters. Examples of this behavior will be given in Section 7.
Another important characteristic of the system, which can be deduced by the simple model derived in this section, is that only the first part of the water column contributes significantly to the received power. In fact, it is easy to see that the integrand in (46) rapidly goes to zero for  grater than a certain maximum value
grater than a certain maximum value  (see Figure 1), which, for physically sensible choices of the parameters, results of the order of a few meters. This suggests an experimental method for assessing the water component of the total power measured when shooting the laser beam onto a target at a distance
(see Figure 1), which, for physically sensible choices of the parameters, results of the order of a few meters. This suggests an experimental method for assessing the water component of the total power measured when shooting the laser beam onto a target at a distance  from the receiver. Provided the water column between the receiver and the target is long enough to encompass all the relevant contributions from water scatterers (i.e.,
from the receiver. Provided the water column between the receiver and the target is long enough to encompass all the relevant contributions from water scatterers (i.e.,  ), the water backscattered power in presence of the target can be quite accurately estimated by preliminarily shooting the beam in open water (i.e., in the absence of any close-by reflecting surfaces). This simple technique would obviously overestimate the real water component to the total signal if
), the water backscattered power in presence of the target can be quite accurately estimated by preliminarily shooting the beam in open water (i.e., in the absence of any close-by reflecting surfaces). This simple technique would obviously overestimate the real water component to the total signal if  .
.
4. Interference-Like Effect between Medium and Target Signals in Underwater AM Imagers
Signal detection in an AM laser optical radar is typically provided by a phase-sensitive device, such as a lock-in amplifier, which is also used to set the working modulation frequency  of the laser source. The lock-in amplifier selectively amplifies only the component of the input signal that oscillates at the same frequency of a reference signal—that is, in the case at hand, the modulation frequency
of the laser source. The lock-in amplifier selectively amplifies only the component of the input signal that oscillates at the same frequency of a reference signal—that is, in the case at hand, the modulation frequency  —, permitting a better discrimination of signal from noise.
—, permitting a better discrimination of signal from noise.
In ideal conditions, that is neglecting the contribution of water backscattering, the amplitude  and phase
and phase  of the detected signal coincide with the so-called target signal, that is, are directly related to the target backscattered intensity and range, respectively. The presence of the medium, though, introduces a further signal component (often called optical noise in this work), which combines with the target signal on the detector.
of the detected signal coincide with the so-called target signal, that is, are directly related to the target backscattered intensity and range, respectively. The presence of the medium, though, introduces a further signal component (often called optical noise in this work), which combines with the target signal on the detector.
In complex notation, neglecting possible contributions from objects other than the target and any other noise sources, the signal  measured by the lock-in amplifier results to be the sum of two major components:
measured by the lock-in amplifier results to be the sum of two major components:

where  is the signal due to the target, that carries the all relevant information, and
is the signal due to the target, that carries the all relevant information, and  is the cumulative contribution of light backscattered by the water column interposed between the target and the receiver.
is the cumulative contribution of light backscattered by the water column interposed between the target and the receiver.
As shown in the previous section, the amplitude and phase of the optical noise signal generally depend on  —as well as on system parameters such as
—as well as on system parameters such as  and
and  , the length of the water column between target and receiver measured along the laser beam propagation direction. For an ideal Lambertian diffuser in single backscattering regime, on the other hand,
, the length of the water column between target and receiver measured along the laser beam propagation direction. For an ideal Lambertian diffuser in single backscattering regime, on the other hand,  , while
, while  does not depend on
does not depend on  .
.
From (50), the amplitude and phase of the detected signal are easily obtained:

where we have introduced the dimensionless parameter  and
and  denotes the phase difference between target and water signals, varying in the interval
denotes the phase difference between target and water signals, varying in the interval  and generally depending on
and generally depending on  .
.
The expression for  shows an interference-like effect between target and water signals for varying
shows an interference-like effect between target and water signals for varying  , due to term
, due to term  . Because of this term, one generally expects to observe oscillations of
. Because of this term, one generally expects to observe oscillations of  as a function of the modulation frequency. Oscillations disappear when
as a function of the modulation frequency. Oscillations disappear when  is much smaller or considerably larger than
is much smaller or considerably larger than  , corresponding to the cases
, corresponding to the cases  and
and  , respectively.
, respectively.
When  , from (51) one obtains
, from (51) one obtains

that is the detected signal practically corresponds to the target signal. On the contrary, when  one has
one has

namely, the detected signal is only due to water, and its dependence on  shows the typical low-pass filter trend (see (49) and following remarks).
shows the typical low-pass filter trend (see (49) and following remarks).
In all intermediate cases, the effect of the medium on the detected signal produces fluctuations of  at varying
at varying  , due to the roughly linear expected dependence of
, due to the roughly linear expected dependence of  on the modulation frequency.
on the modulation frequency.
The signal-to-optical-noise ratio  and the contrast
and the contrast 
 , defined as
, defined as

also oscillate at varying modulation frequency, with local maxima and minima corresponding to the same values of  . These values depend in turn on
. These values depend in turn on  and
and  , as will be shown in Section 8. Moreover,
, as will be shown in Section 8. Moreover,  and
and  increase with
increase with  , because of the decrease of
, because of the decrease of  due to the low-pass filter response of water backscattering as a function of the modulation frequency.
due to the low-pass filter response of water backscattering as a function of the modulation frequency.
The previous simple analysis suggests a method for reducing the effect of water backscattering. The method is based on the experimental determination of  (i.e., both
(i.e., both  and
and  ) through a series of preliminary measurements at different values of the modulation frequency, carried out by shooting the laser light in open water in the vicinity of the target. The target signal can then be estimated by subtracting the measured water backscattering from the total signal detected when shooting onto the target. Indeed, from the trivial relationship
) through a series of preliminary measurements at different values of the modulation frequency, carried out by shooting the laser light in open water in the vicinity of the target. The target signal can then be estimated by subtracting the measured water backscattering from the total signal detected when shooting onto the target. Indeed, from the trivial relationship  and, proceeding as before, one easily obtains
and, proceeding as before, one easily obtains

where the new dimensionless parameter  takes the form
takes the form

and  represents the phase difference between the detected and water signals:
represents the phase difference between the detected and water signals:

The reliability of the estimated target signal can be assessed by verifying that  and the newly defined quantities
and the newly defined quantities  and
and  ,
,

grow monotonically for increasing  , with no or sensibly reduced oscillations.
, with no or sensibly reduced oscillations.
The viability of the method ultimately relies on the practicability of measuring  in real operating conditions, as well as on the validity of the implicit assumption that the water backscattering measured in open water can be used as an estimation of the contribution from the finite water column of length
in real operating conditions, as well as on the validity of the implicit assumption that the water backscattering measured in open water can be used as an estimation of the contribution from the finite water column of length  when the target is present. As shown in the previous section, this assumption is approximately correct as long as
when the target is present. As shown in the previous section, this assumption is approximately correct as long as  is larger than a certain maximum value
is larger than a certain maximum value  —depending on
—depending on  and other parameters, such as the angular field of view of the receiver—, beyond which the light backscattered off water and entering the receiver becomes negligible. In fact, we have verified through numerical simulations that, for water of moderate turbidity,
and other parameters, such as the angular field of view of the receiver—, beyond which the light backscattered off water and entering the receiver becomes negligible. In fact, we have verified through numerical simulations that, for water of moderate turbidity,  is typically of the order of a few meters.
is typically of the order of a few meters.
5. Polarization Properties of Medium and Target Backscattering
A distinct approach for the enhancement of underwater 3D images consists in exploiting the difference in polarization of light backscattered by the medium from light reflected by the target [13, 22–26]. The method relies on the fact that, at least in certain conditions, linearly polarized incident light is partially depolarized by the target, while backscattering off the medium conserves the polarization state. A similar phenomenon occurs in case of circular polarization, where helicity is reversed by the medium but not by the target. Beside underwater imaging, other application fields of this method are remote sensing [27] and biomedical studies [28], where its effectiveness is demonstrated.
The phenomenology underlying the polarimetric technique is better expressed by using the Stokes-Mueller formalism [29], which enables one to completely describe the intensity and the polarization state of radiation by means of Stokes vectors, and the medium or target effect on the light polarization state through Mueller matrices.
The Stokes vector  is a four-component column array defined as:
is a four-component column array defined as:

The elements of  , also-called Stokes parameters, can be expressed in terms of the electric field components, parallel and perpendicular to the scattering plane, respectively. In particular,
, also-called Stokes parameters, can be expressed in terms of the electric field components, parallel and perpendicular to the scattering plane, respectively. In particular,  represents the radiation intensity while
represents the radiation intensity while  ,
,  and
and  denote the radiation polarization state.
denote the radiation polarization state.
Scattered light usually has a different polarization state compared to incident radiation, as a consequence of light-matter interaction. The depolarization action of either the medium or the target on incident light can be expressed by means of a  Mueller matrix
Mueller matrix  , also-called scattering or polarization matrix. If
, also-called scattering or polarization matrix. If  describes the intensity and polarization state of incoming light, the Stokes vector
describes the intensity and polarization state of incoming light, the Stokes vector  of scattered radiation is given by
of scattered radiation is given by

where  is the radiation wavenumber and
is the radiation wavenumber and  the distance from detector.
the distance from detector.
The element  of the Muller matrix represents the intensity distribution of scattered light into different directions, and is directly related to the phase function. Depolarizing effects are better emphasized in terms of the normalized or reduced Mueller matrix
of the Muller matrix represents the intensity distribution of scattered light into different directions, and is directly related to the phase function. Depolarizing effects are better emphasized in terms of the normalized or reduced Mueller matrix  , with elements
, with elements  (
( ).
).
The depolarization degree can also be quantified by means of either of the two following macroscopic parameters:

These parameters, called depolarization effect ( ) and depolarization index (
) and depolarization index ( ), respectively, provide an average measurement of the depolarizing action of an optical system (target, medium, etc.). In particular, if
), respectively, provide an average measurement of the depolarizing action of an optical system (target, medium, etc.). In particular, if  ,
,  the scattered light is completely depolarized, while if
the scattered light is completely depolarized, while if  ,
,  the scattered light preserves the polarization state after the interaction with matter. All the other values of
the scattered light preserves the polarization state after the interaction with matter. All the other values of  and
and  correspond to partial depolarization.
correspond to partial depolarization.
In order to evaluate the effectiveness of polarization discrimination as a means for improving the accuracy and the performances of a laser imaging system, we will analyze the depolarizing effect on the light polarization state due to the medium and the target, respectively.
The different scattering regimes are usually characterized in terms of the dimensionless size parameter  , related to the radius
, related to the radius  of a typical scattering particle (scatterer) by the expression:
of a typical scattering particle (scatterer) by the expression:

with  the refractive index of the medium.
the refractive index of the medium.
Depending on the values assumed by this parameter, it is possible to distinguish three different scattering regimes: ( ) Rayleigh, when
) Rayleigh, when  (small particles, radiation is isotropically scattered); (
(small particles, radiation is isotropically scattered); ( ) intermediate, when
) intermediate, when  (scattered radiation begins to be forward peaked); (
(scattered radiation begins to be forward peaked); ( ) Mie, when
) Mie, when  (large particles, scattered radiation is mostly concentrated in the forward direction and scattering is anisotropic).
(large particles, scattered radiation is mostly concentrated in the forward direction and scattering is anisotropic).
We initially consider the depolarization effects of clean water with spherical Rayleigh scatterers, where absorption can be neglected and single scattering events are predominant. The normalized Mueller matrix can be written in this case as [30, 31]:

where

(Note that, although not explicitly indicated,  generally also depends on the refractive index and the size parameter of the scatterers.) The elements of the normalized Mueller matrix have specific meanings. Specifically,
generally also depends on the refractive index and the size parameter of the scatterers.) The elements of the normalized Mueller matrix have specific meanings. Specifically,  indicates the deviation of scattering particles from the spherical shape, being
indicates the deviation of scattering particles from the spherical shape, being  and
and  for spherical and non spherical scatterers, respectively. When
for spherical and non spherical scatterers, respectively. When  , this element contributes to the depolarization of light with vertical or horizontal linear polarization (Vertical and horizontal linear polarization states are defined in terms of a given reference plane, usually the scattering plane, defined by the incidence and scattering directions. ). The
, this element contributes to the depolarization of light with vertical or horizontal linear polarization (Vertical and horizontal linear polarization states are defined in terms of a given reference plane, usually the scattering plane, defined by the incidence and scattering directions. ). The  element also contributes to the degree of vertical or horizontal linear depolarization, irrespectively from the shape of scatterers, but depending on their size, geometry and optical properties.
element also contributes to the degree of vertical or horizontal linear depolarization, irrespectively from the shape of scatterers, but depending on their size, geometry and optical properties.  indicates how much of ±45° linearly polarized light is preserved after the scattering event. Finally,
indicates how much of ±45° linearly polarized light is preserved after the scattering event. Finally,  is a measure of the fraction of circularly polarized light preserved after the scattering process. For negative values, this element also accounts for the helicity flip phenomenon.
is a measure of the fraction of circularly polarized light preserved after the scattering process. For negative values, this element also accounts for the helicity flip phenomenon.
In backscattering conditions ( ),
),  reads
reads

From the form of  , one immediately concludes that, for spherical particles in the Rayleigh scattering regime, the radiation backscattered at
, one immediately concludes that, for spherical particles in the Rayleigh scattering regime, the radiation backscattered at  preserves the vertical or horizontal linear polarization state of the incident light (since
preserves the vertical or horizontal linear polarization state of the incident light (since  ,
,  ). On the other hand, the helicity of circularly polarized light is reversed (helicity flip) by
). On the other hand, the helicity of circularly polarized light is reversed (helicity flip) by  .
.
As a second step, we consider turbid water obtained by adding skim milk to clean water. Homogenized skim milk is an optimal light diffusing material, characterized by an elevated solubility in water. Its scattering elements (mainly proteins and fats) can be considered as spherical particles with an average diameter of  [32]. In these conditions, the scattering of laser light used in underwater imaging systems, typically in the visible region of electromagnetic spectrum (
[32]. In these conditions, the scattering of laser light used in underwater imaging systems, typically in the visible region of electromagnetic spectrum ( ), falls in the intermediate regime.
), falls in the intermediate regime.
The normalized Mueller matrix of an optically thin mixture of skim milk and water has the following form [33–35]:

(The expression applies in general to isotropic symmetrical media with spherical scatterers of arbitrary dimensions in the conditions of the intermediate and Mie single scattering regimes. ) is structurally similar to
is structurally similar to  , with the important difference represented by the elements
, with the important difference represented by the elements  —measuring the fraction of linearly polarized light transformed into circularly polarized radiation- and
—measuring the fraction of linearly polarized light transformed into circularly polarized radiation- and  , which are now different from zero.
, which are now different from zero.
In the intermediate or Mie scattering regimes, the scattering pattern of the medium is forward peaked and characterized by a larger scattering efficiency factor than in the Rayleigh regime. Moreover, depolarization degree becomes a more and more rippled function of the scattering angle. Nonetheless, as long as multiple scattering events are negligible (optically thin medium) and polarization memory effects [36] don't occur, it is possible to show that, at backscattering,  is similar to
is similar to  , so that also in this case linear polarization is preserved, and circular polarization is subject to helicity flip. More precisely, measurements performed on skim milk diluted in deionized water [35] show that, if the mixture is optically thin and in the approximation of spherical scatterers,
, so that also in this case linear polarization is preserved, and circular polarization is subject to helicity flip. More precisely, measurements performed on skim milk diluted in deionized water [35] show that, if the mixture is optically thin and in the approximation of spherical scatterers,  deviates only slightly from the
deviates only slightly from the  behavior, typical of the Rayleigh scattering regime, while
behavior, typical of the Rayleigh scattering regime, while  assumes negative values for
assumes negative values for  .
.
In conclusion, optically thin turbid water combines a quasi-Rayleigh depolarization pattern with the high scattering efficiency typical of a quasi-Mie regime.
We finally take into account the depolarization effect due to a diffusive Lambertian target, such as a painted metal object, immersed in distilled water. In this case, the normalized Mueller matrix at backscattering can be written in the form [30]

The values of  and
and  suggest that such a target behaves as a depolarizing element, which randomizes the polarization state and helicity of scattered light (
suggest that such a target behaves as a depolarizing element, which randomizes the polarization state and helicity of scattered light ( , and
, and  and negative). This is due to multiple scattering events occurring beneath the paint layer, which acts as a volume scatterer.
and negative). This is due to multiple scattering events occurring beneath the paint layer, which acts as a volume scatterer.
By applying the Stokes-Mueller formalism to the particular case of radiation with horizontal linear polarization-represented by the Stokes vector  -hitting the target perpendicularly, we obtain in backscattering conditions:
-hitting the target perpendicularly, we obtain in backscattering conditions:

In this case, we see that only 61% of the radiation backscattered by the target preserves the initial polarization state ( ). The remaining fraction of backscattered light is completely depolarized.
). The remaining fraction of backscattered light is completely depolarized.
A similar result is obtained for circularly polarized incident light, considering in this case also the helicity flip due to the negative value of  . For example, for incident light with right-hand circular polarization, represented by
. For example, for incident light with right-hand circular polarization, represented by  , we get
, we get

So, the effect of a diffusive Lambertian target is to randomize the polarization state of incident radiation.
The results obtained in this section permit to conclude that polarimetric techniques can effectively improve the accuracy of an underwater 3D imager, provided the system is capable of discriminating the various polarization states of incident and backscattered light.
In fact, in single backscattering conditions with  , water—both clean and turbid, as long as single scattering is the main mechanism involved—does not depolarize the incident light, preserving the linear polarization and reversing the helicity of the circular polarization. On the contrary, the effect of diffusive Lambertian targets is to partially depolarize the backscattered light, by an amount which depends on the characteristics of the target surface (roughness, type of material, etc.) as well as on the incidence and observation directions.
, water—both clean and turbid, as long as single scattering is the main mechanism involved—does not depolarize the incident light, preserving the linear polarization and reversing the helicity of the circular polarization. On the contrary, the effect of diffusive Lambertian targets is to partially depolarize the backscattered light, by an amount which depends on the characteristics of the target surface (roughness, type of material, etc.) as well as on the incidence and observation directions.
Consequently, by controlling the radiation polarization state of the transmitter and receiver stages through suitable combinations of polarizers (linearly and circularly copolarized or cross-polarized working schemes, depending on radiation polarization state and polarization memory effects), it is possible to distinguish the depolarized component backscattered by the target from the total received radiation. This permits to reject the received signal component due to scattering off the medium (optical noise), and improve the performances (signal-to-optical-noise ratio, contrast, target visibility range and phase measurement accuracy) of the underwater imager.
It is important to notice that also the medium starts depolarizing as the optical thickness  increases, owing to the higher and higher rate of multiple scattering events, which eventually dominate over single scattering. In this regime, polarization is not preserved by the medium anymore. Irregularities and asymmetries in the shape of scatterers can also significantly contribute to the depolarization effect.
increases, owing to the higher and higher rate of multiple scattering events, which eventually dominate over single scattering. In this regime, polarization is not preserved by the medium anymore. Irregularities and asymmetries in the shape of scatterers can also significantly contribute to the depolarization effect.
Experimental results showing the effectiveness of the suggested polarimetric technique for the reduction of optical noise in underwater AM laser imagers are reported in Section 9.
5.1. Part II-Experimental Results
In the following sections we report a series of underwater 3D imaging experimental results obtained by using a bistatic AMULOR imager prototype, equipped with a phase-intensity sensitive lock-in detector. The experiments are aimed at: ( ) verifying the theoretical results described in the first part of this work; (
) verifying the theoretical results described in the first part of this work; ( ) developing techniques that enable the effective rejection of the signal due to light backscattered off water (optical noise), in view of the realization of an operational AMULOR imager for underwater archaeology applications.
) developing techniques that enable the effective rejection of the signal due to light backscattered off water (optical noise), in view of the realization of an operational AMULOR imager for underwater archaeology applications.
The system setup is described in detail in the Section 6. The subsequent three sections are then, respectively, dedicated to
-
(1)
the experimental verification of the low-pass filter behavior of the water backscattering signal, directly measured in a black-walled 25m long test tank, and compared with the theoretical results of Section 3;
-
(2)
the experimental confirmation and possible exploitation of the expected interference-like effect in the signal detected by the AMULOR as a function of
 , due to the overlapping between target and water signals (see Section 4);
, due to the overlapping between target and water signals (see Section 4); -
(3)
the application of the polarimetric technique outlined in Section 5 as an alternative or complementary method for optical noise rejection.
6. Experimental Apparatus
The optical layout of the bistatic AMULOR system, designed and realized at the ENEA Artificial Vision Laboratory in Frascati (Rome, Italy) and used for underwater 3D imaging, is depicted in Figure 2.
The laboratory prototype consists of a launching module (laser source, single-mode connection optical fiber with core diameter of  , and launching optics), a receiving module (receiving optics, multimode connection optical fiber with core diameter of 1 mm, photomultiplier and lock-in amplifier) and a Plexiglas test tank, filled with water of varying turbidity and equipped with an anti-reflection coated entrance optical window.
, and launching optics), a receiving module (receiving optics, multimode connection optical fiber with core diameter of 1 mm, photomultiplier and lock-in amplifier) and a Plexiglas test tank, filled with water of varying turbidity and equipped with an anti-reflection coated entrance optical window.
The radiation source is a collimated low power diode laser emitting 20 mW of blue-violet continuous-wave light at  . The intensity of the laser light is sinusoidally modulated at frequencies
. The intensity of the laser light is sinusoidally modulated at frequencies  up to 200 MHz by using a lock-in amplifier. An aspheric, computer-optimised, 7 mm-
up to 200 MHz by using a lock-in amplifier. An aspheric, computer-optimised, 7 mm- short-focal lens focuses the modulated beam onto the target (laser spot size
short-focal lens focuses the modulated beam onto the target (laser spot size  at 2 m), which is placed in a test tank at a distance
at 2 m), which is placed in a test tank at a distance  from the entrance window.
from the entrance window.
Depending on experimental needs, the laser beam can either be shot on a fixed point of the target or swept by means of a piezoelectric scanning system, consisting of a focusing lens mounted on a pair of mutually orthogonal linear piezoelectric translators.
According to the type of underwater imaging experiment, two different Plexiglas test tanks can be used, with length equal to 1.56 m and 25 m, and a total capacity of about 27 and 6000 liters, respectively.
Backscattered light is collected and focused onto a fast photomultiplier detector (Hamamatsu H5783) with circular sensible area of radius 4 mm. The receiver field of view semiangle, calculated by taking into account the refraction on the air-water interface, is  .
.
Intensity and phase shift—with respect to a reference signal—of backscattered radiation are measured by means of the same lock-in amplifier used to modulate the laser beam. The adopted bistatic optical layout—that is, the spatial separation  between the light source and the receiver-permits a partial reduction of detected stray light by limiting the transmitter and receiver common field of view (see (46)). The spatial separation
between the light source and the receiver-permits a partial reduction of detected stray light by limiting the transmitter and receiver common field of view (see (46)). The spatial separation  is 7 cm for the smaller tank and 20 cm for the longer one. Since both these values are much less than the typical target distances
is 7 cm for the smaller tank and 20 cm for the longer one. Since both these values are much less than the typical target distances  , the apparatus can be considered quasi-monostatic with good approximation and
, the apparatus can be considered quasi-monostatic with good approximation and  practically coincides with the distance
practically coincides with the distance  measured along the laser beam propagation direction.
measured along the laser beam propagation direction.
In the polarimetric imaging experiments, the polarization control on both the launching and receiving stages is obtained through suitable combinations of Glan-Thompson polarizers and quarter wave plates.
7. Dependence of Optical Noise on the Modulation Frequency in an Underwater AM Imagers
In these experiments we directly measured the water backscattering signal, in order to experimentally verify the low-pass filter behavior of the optical noise versus the modulation frequency  . We used the AMULOR system of Figure 2, comprising a black-walled 25 m long test tank, with
. We used the AMULOR system of Figure 2, comprising a black-walled 25 m long test tank, with  ,
,  , and a receiver of radius
, and a receiver of radius  . The AM laser beam was shot in a fixed direction onto the 25 m long water column without interposed target, and the retro-diffused radiation measured by varying
. The AM laser beam was shot in a fixed direction onto the 25 m long water column without interposed target, and the retro-diffused radiation measured by varying  in the range 0.5÷ 138 MHz.
in the range 0.5÷ 138 MHz.
Two series of experiments were carried out, with water attenuation coefficients  and
and  , respectively, measured by using a PerkinElmer Lambda 25 UV/vis spectrometer. In both cases, we verified that the laser light was completely attenuated in correspondence of the tank bottom. Experimental results were compared with the expected theoretical outcomes, calculated by means of (46).
, respectively, measured by using a PerkinElmer Lambda 25 UV/vis spectrometer. In both cases, we verified that the laser light was completely attenuated in correspondence of the tank bottom. Experimental results were compared with the expected theoretical outcomes, calculated by means of (46).
Figure 3 shows an example of this comparison for  . Theoretical and experimental data are normalized to their maximum values. The theoretical curve in dashed line was calculated by neglecting absorption and in the simplistic hypothesis that single scattering in the backward direction is the only attenuation mechanism, that is, by using the following values for the parameters:
. Theoretical and experimental data are normalized to their maximum values. The theoretical curve in dashed line was calculated by neglecting absorption and in the simplistic hypothesis that single scattering in the backward direction is the only attenuation mechanism, that is, by using the following values for the parameters:  =
=  =
=  =
=  ,
,  . Conversely, the solid curve corresponds to the more realistic conditions:
. Conversely, the solid curve corresponds to the more realistic conditions:  ,
,  (note that
(note that  =
=  ),
),  .
.
These parameters were estimated by making some reasonable assumptions on the values of  ,
,  , which we could not measure directly, and
, which we could not measure directly, and  (recall that
(recall that  ), in an attempt to reproduce the experimental conditions.
), in an attempt to reproduce the experimental conditions.  was estimated using (33) with the assumption
was estimated using (33) with the assumption

where  is the Henyey-Greenstein phase function [37] and
is the Henyey-Greenstein phase function [37] and  is the asymmetry factor, which represents the mean value of the cosine of the scattering angle. For values of the asymmetry factor close to 1,
is the asymmetry factor, which represents the mean value of the cosine of the scattering angle. For values of the asymmetry factor close to 1,  provides a good approximation of the course-grain characteristics of typical phase functions of natural waters.
provides a good approximation of the course-grain characteristics of typical phase functions of natural waters.
In fact, since in natural waters most of the energy is contained in a narrow peak at scattering angles less than 10°–15° [17], as a consequence of scattering events from suspended large particles typical of intermediate or Mie regimes, it is reasonable to assume  . The value
. The value  corresponds to
corresponds to  .
.
The cut-off frequency, calculated as the frequency at which the power is  of the maximum value, is
of the maximum value, is  for the simplistic model, and
for the simplistic model, and  for the more realistic case. On the other hand, by fitting the normalized experimental data by means of the classical low-pass filter formula
for the more realistic case. On the other hand, by fitting the normalized experimental data by means of the classical low-pass filter formula

where  is a free parameter, we obtain the estimate
is a free parameter, we obtain the estimate  . This value is in good accordance with
. This value is in good accordance with  and coincides, within the error, with
and coincides, within the error, with  , showing that the proposed theoretical model provides a satisfactory description of the experiment, especially in the more realistic case where absorption and laser beam spread are taken into account.
, showing that the proposed theoretical model provides a satisfactory description of the experiment, especially in the more realistic case where absorption and laser beam spread are taken into account.
The previous conclusion is confirmed by the analysis of Figure 4, where we report theoretical predictions and measurements made at  . Also in this case, the dashed line corresponds to
. Also in this case, the dashed line corresponds to  ,
,  (no absorption, pure single backscattering). The solid line, on the other hand, was obtained by using for the parameters the estimated values
(no absorption, pure single backscattering). The solid line, on the other hand, was obtained by using for the parameters the estimated values  ,
,  , and
, and  , which corresponds to
, which corresponds to  in (70). Note that
in (70). Note that  is greater than the corresponding value for
is greater than the corresponding value for  . In fact, an increase of
. In fact, an increase of  is to be expected when the multiple scattering rate in the forward direction at small angles increases, as a consequence of the growing concentration of scattering elements.
is to be expected when the multiple scattering rate in the forward direction at small angles increases, as a consequence of the growing concentration of scattering elements.
The theoretical values of the cut-off frequency for the curves of Figure 4 are  and
and  , to be compared with the experimental estimate
, to be compared with the experimental estimate  .
.
Figures 3 and 4 confirm the expected low-pass filter trend, and clearly show that, if a phase-intensity sensitive system such as a lock-in is used for backscattered light detection, an effective optical noise rejection can be achieved by increasing the laser modulation frequency beyond the cut-off frequency. The slight yet appreciable oscillations of experimental data in Figures 3 and 4 are possibly due to multiple backward scattering contributions not considered in the present theoretical model.
In support of this fundamental result, we report in Figures 5 and 6 the 3D images of a small dark-gray-painted, sanded, metallic ladder, both obtained in optically thin water. Specifically, in Figure 5 the target was immersed in clean tap water ( ) at a distance of 1.5 m from the receiver. Incident light was modulated at frequency
) at a distance of 1.5 m from the receiver. Incident light was modulated at frequency  , higher than water cut-off frequency [3]. The other image was obtained in conditions of relatively turbid water (
, higher than water cut-off frequency [3]. The other image was obtained in conditions of relatively turbid water ( ) with a target-receiver distance of 3.7
) with a target-receiver distance of 3.7 m. The modulation frequency
m. The modulation frequency  was, in this case, just beyond the expected cut-off value.
was, in this case, just beyond the expected cut-off value.
Both the pictures are of good quality, and rather faithfully reproduce the original target. A slight degradation of the phase (i.e., distance) measurement accuracy is observable in Figure 6, evidenced by a rougher and less sharp reproduction of the ladder. This can be attributed to the much higher optical thickness of the medium in this case, with a consequent increase of the cut-off frequency, that would have required to operate at a much higher modulation frequency.
8. Verification of the Interference-Like Effect and Methods for Optical Noise Cancellation
As shown in Section 4, by shooting an AM laser beam at increasing modulation frequencies on an underwater target at fixed distance, an interference-like overlapping between water and target backscattering signals ( and
and  , resp.) should be observed, if a phase-intensity sensitive system such as a lock-in amplifier is used for backscattered light detection. (See Section 4 for an explanation of the notations.) In particular, when the two contributions are comparable, the amplitude of detected signal
, resp.) should be observed, if a phase-intensity sensitive system such as a lock-in amplifier is used for backscattered light detection. (See Section 4 for an explanation of the notations.) In particular, when the two contributions are comparable, the amplitude of detected signal  , contrast
, contrast  and signal-to-optical-noise ratio
and signal-to-optical-noise ratio  are expected to oscillate with the modulation frequency [2, 10–12], with local maxima and minima corresponding to values of
are expected to oscillate with the modulation frequency [2, 10–12], with local maxima and minima corresponding to values of  that generally depend on the water attenuation coefficient
that generally depend on the water attenuation coefficient  , position of the target
, position of the target  and transmitter-receiver separation
and transmitter-receiver separation  .
.  and
and  are also expected to have an increasing trend with the modulation frequency, owing to the low-pass filter behavior of the optical noise (see Sections 3 and 7).
are also expected to have an increasing trend with the modulation frequency, owing to the low-pass filter behavior of the optical noise (see Sections 3 and 7).
This effect could be used to improve the accuracy of both intensity and phase measurements, by appropriately selecting the working modulation frequency in correspondence of one of the local maxima of  ,
,  and
and  —better if higher than the cut-off frequency.
—better if higher than the cut-off frequency.
In order to experimentally verify the interference-like effect, a means is needed to disentangle the optical noise due to water backscattering from the detected total signal  . This necessarily requires the ability to measure the optical noise independently, that is, in the absence of the target. Furthermore, it should be verified that the noise signal measured in this way is the same that would be revealed when the target is present. The last requirement poses a constraint on the target distance
. This necessarily requires the ability to measure the optical noise independently, that is, in the absence of the target. Furthermore, it should be verified that the noise signal measured in this way is the same that would be revealed when the target is present. The last requirement poses a constraint on the target distance  , which should be greater than the distance
, which should be greater than the distance  after which the water column does not contribute appreciably to the total noise (see Figure 1).
after which the water column does not contribute appreciably to the total noise (see Figure 1).
A series of experiments were performed to this aim by means of the AMULOR system prototype of Figure 2. The system configuration was the same as for the measurements reported in the previous section. Experiments were carried out by launching an AM laser beam in a fixed direction onto a white, flat, 34 cm  44 cm—mostly diffusive, yet non-calibrated—target and measuring the backscattered radiation. The target was placed at various distances from the receiving stage in a black-walled 25 m long test tank, filled with water of two different turbidity levels.
44 cm—mostly diffusive, yet non-calibrated—target and measuring the backscattered radiation. The target was placed at various distances from the receiving stage in a black-walled 25 m long test tank, filled with water of two different turbidity levels.
We report in the following the results of three different experiments, characterized by the following values of the relevant parameters:
-
(1)
 and
and 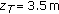 (
( on average),
on average), -
(2)
 and
and 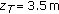 (
(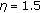 on average),
on average), -
(3)
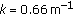 and
and 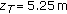 (
(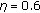 on average).
on average).
In all cases, the experimental conditions corresponded to the transition regime between single and multiple scattering, since the optical thickness was  [38]. The quantities
[38]. The quantities  and
and  were measured independently, at modulation frequencies
were measured independently, at modulation frequencies  varying in the range (0.5–146) MHz. In particular, the measurements of
varying in the range (0.5–146) MHz. In particular, the measurements of  were carried out by shooting the laser beam in the 25 m long tank with no interposed target, after verifying that the beam did not reach tank bottom. The formulas derived in Section 4 were applied for calculating the quantities
were carried out by shooting the laser beam in the 25 m long tank with no interposed target, after verifying that the beam did not reach tank bottom. The formulas derived in Section 4 were applied for calculating the quantities  ,
,  ,
,  ,
,  and
and  and analyzing their dependence on
and analyzing their dependence on  .
.
Although  and
and  were not measured in identical experimental conditions,
were not measured in identical experimental conditions,  represents a good approximation of the optical noise component of
represents a good approximation of the optical noise component of  for sufficiently large
for sufficiently large  , since the optical noise signal is dominated by light backscattered in the first few meters of the water column.
, since the optical noise signal is dominated by light backscattered in the first few meters of the water column.
Figure 7 reports a comparison of the amplitudes  (measured) and
(measured) and  (calculated)—normalized to the mean value of input laser power and to modulation index—for the three experiments.
(calculated)—normalized to the mean value of input laser power and to modulation index—for the three experiments.
Figure 7 on top represents a situation where the amplitude  of the water signal is much less than
of the water signal is much less than  (
( ). As a consequence, the interference between the two signals is very weak, and the removal of
). As a consequence, the interference between the two signals is very weak, and the removal of  from the detected signal
from the detected signal  does not produce sensible effects.
does not produce sensible effects.
The central part of Figure 7 represents the case where the amplitudes  and
and  are comparable, with
are comparable, with  . In this situation, the oscillations of
. In this situation, the oscillations of  are evident, with regular maxima and minima separations in the range (33.5–43.4) MHz. The removal of the water contribution from the detected signal permits in this case to strongly reduce the oscillations of
are evident, with regular maxima and minima separations in the range (33.5–43.4) MHz. The removal of the water contribution from the detected signal permits in this case to strongly reduce the oscillations of  as a function of
as a function of  . The presence of very small fluctuations in
. The presence of very small fluctuations in  can be ascribed to an overestimation of
can be ascribed to an overestimation of  —indeed, we could not experimentally verify the condition
—indeed, we could not experimentally verify the condition  —, as well as to noise sources not considered in our treatment, such as for instance the contribution of light reflected from tank walls.
—, as well as to noise sources not considered in our treatment, such as for instance the contribution of light reflected from tank walls.
On the bottom of Figure 7,  and
and  are again comparable, with
are again comparable, with  . Also in this case,
. Also in this case,  is strongly oscillating as a function of
is strongly oscillating as a function of  , and maxima and minima are regularly distributed, though with a different frequency separation of about 25 MHz. Conversely,
, and maxima and minima are regularly distributed, though with a different frequency separation of about 25 MHz. Conversely,  , obtained from
, obtained from  by removing the optical noise signal, shows almost no oscillations.
by removing the optical noise signal, shows almost no oscillations.
A similar behavior is also observed in the plots reporting  and
and  as a function of
as a function of  (Figures 8 and 9). Both these quantities oscillate—with maxima and minima lying at the same values of
(Figures 8 and 9). Both these quantities oscillate—with maxima and minima lying at the same values of  observed for
observed for  —when water and target signals are comparable, while they increase almost monotonically if
—when water and target signals are comparable, while they increase almost monotonically if  or
or  , that is, if one of two component signals is clearly prevailing. It is also evident that both
, that is, if one of two component signals is clearly prevailing. It is also evident that both  and
and  grow with
grow with  , owing to the low-pass filter frequency response of water backscattering. This constitutes a further evidence of the general tendency of an AMULOR system to improve its performances as
, owing to the low-pass filter frequency response of water backscattering. This constitutes a further evidence of the general tendency of an AMULOR system to improve its performances as  increases. Oscillations are again drastically reduced for the (calculated) quantities
increases. Oscillations are again drastically reduced for the (calculated) quantities  and
and  whenever
whenever  , with no significant effect in the other cases (
, with no significant effect in the other cases ( or
or  ).
).
Finally, by comparing the trends of  ,
,  and
and  ,
,  , one can observe that, for some values of
, one can observe that, for some values of  , both
, both  and
and  are less than 1, while
are less than 1, while  and
and  are negative, owing to the dominance of the optical noise over the target signal.
are negative, owing to the dominance of the optical noise over the target signal.
These results, beside constituting a further experimental proof of the existence of the interference-like effect [2], confirm—as firstly suggested in [10]—the possibility to improve the performances of an underwater amplitude-modulated 3D imager by working at modulation frequencies opportunely selected so as to correspond to the local maxima of  ,
,  and
and  , even below the cut-off frequency.
, even below the cut-off frequency.
On the other hand, even when the exact position of the local maxima cannot be determined a priori, it is still possible to reduce the deleterious effects of the optical noise by direct cancellation, provided the water backscattering signal can be measured independently by shooting in open water.
9. Optical Noise Rejection through Polarimetry
In this section we report a series of underwater 3D images and linear phase profiles, obtained by using the AMULOR system of Figure 2, equipped with suitable polarizer configurations on the launching and receiving stages and a 1.56 m Plexiglas test tank, with source-receiver separation  . The experiments were aimed at demonstrating the validity of the polarimetric technique proposed in Section 5 as an effective means to reduce the effect of optical noise on both intensity and phase measures.
. The experiments were aimed at demonstrating the validity of the polarimetric technique proposed in Section 5 as an effective means to reduce the effect of optical noise on both intensity and phase measures.
A first series of experiments were carried out by perpendicularly sweeping a polarized, AM laser beam on a mostly diffusive target, consisting of a dark-gray-painted, flat, metallic plate. The target was immersed on the bottom of the tank, in water of varying turbidity degrees obtained by adding suitable quantities of skim milk (1.5 wt.% fat content) to tap water. Two polarization schemes were investigated, namely (V, H, R and L stand for "vertical", "horizontal", "right-handed" and "left-handed", resp. ):
-
(1)
incident light in vertical linear polarization state, and receiving stage in either copolarized (VV) or cross-polarized (VH) configuration;
-
(2)
incident light in right-handed circular polarization state, and receiving stage in either copolarized (RR) or cross-polarized (RL) configuration.
In both cases, phase profile lines were acquired, each comprising 80 phase measurements (pixels) with a sampling time for pixel of 100 ms. Each scan line covered a horizontal segment of 10 cm on the target. Owing to the system's bistatic layout, pixels  and
and  corresponded, respectively to the conditions of minimum and maximum overlapping between the receiver field of view and the beam path in water, that is, to minimum and maximum contribution of the optical noise. For each line, the phase was set to 0° in correspondence of pixel
corresponded, respectively to the conditions of minimum and maximum overlapping between the receiver field of view and the beam path in water, that is, to minimum and maximum contribution of the optical noise. For each line, the phase was set to 0° in correspondence of pixel  . Deviations from this value during line scanning (phase drift) were taken as an indication of the optical noise rejection efficiency of the system-lower phase drift values corresponding to higher rejection.
. Deviations from this value during line scanning (phase drift) were taken as an indication of the optical noise rejection efficiency of the system-lower phase drift values corresponding to higher rejection.
The results obtained by using linearly polarized light are reported in Figure 10.
When the flat target is immersed in tap water ( , clean water, Rayleigh scattering regime), there is no appreciable difference between VH and VV configurations. During the scans, the measured phase remains nearly constant within a range of 0.25°, which represents the intrinsic error of the apparatus operating at the described conditions (Figure 10(a)). This occurs because the light backscattered by the tap-water column (optical thickness
, clean water, Rayleigh scattering regime), there is no appreciable difference between VH and VV configurations. During the scans, the measured phase remains nearly constant within a range of 0.25°, which represents the intrinsic error of the apparatus operating at the described conditions (Figure 10(a)). This occurs because the light backscattered by the tap-water column (optical thickness  ) is negligible if compared with the radiation reflected by the target. In fact, in these conditions, the albedo for single scattering events, that represents the fraction of energy lost from incident beam due only to scattering, is close to zero [39].
) is negligible if compared with the radiation reflected by the target. In fact, in these conditions, the albedo for single scattering events, that represents the fraction of energy lost from incident beam due only to scattering, is close to zero [39].
The situation drastically changes for  (
( ), when the condition of quasi-Mie (or intermediate) scattering regime is approached and the light scattered by the medium strongly increases. The phase remains constant-within the accuracy error—along the whole scan line in VH configuration. In the VV scheme, conversely, it grows almost linearly, reaching the value of 1.3° in correspondence of pixel #80, where the detector sees the entire water column (Figure 10(b)). Analogous results are found for
), when the condition of quasi-Mie (or intermediate) scattering regime is approached and the light scattered by the medium strongly increases. The phase remains constant-within the accuracy error—along the whole scan line in VH configuration. In the VV scheme, conversely, it grows almost linearly, reaching the value of 1.3° in correspondence of pixel #80, where the detector sees the entire water column (Figure 10(b)). Analogous results are found for  (Figure 10(c)), where single scattering events still dominate and the medium optical thickness is
(Figure 10(c)), where single scattering events still dominate and the medium optical thickness is  [38, 40].
[38, 40].
In these conditions, the radiation backscattered off water preserves the linear polarization state of the incident light. On the contrary, the target depolarizes, that is, randomly changes the polarization state. As a consequence, the VH detection scheme is more effective in rejecting the optical noise, since in this configuration backscattered light of vertical linear polarization is filtered out, enabling one to obtain phase measurements of higher accuracy.
For  , the medium optical thickness raises up to
, the medium optical thickness raises up to  , approaching the transition scattering regime, with a higher probability of multiple scattering events. In this case, also the light backscattered by the medium is partially depolarized. Consequently, the noise rejection mechanism is less efficient, and the phase measured in the VH configuration presents a nearly linear drift from 0° to 3°. Also in this case, though, the cross-polarized scheme gives better results than the copolarized one, where the phase drift reaches the value of about 7° on the receiver edge (Figure 10(d)).
, approaching the transition scattering regime, with a higher probability of multiple scattering events. In this case, also the light backscattered by the medium is partially depolarized. Consequently, the noise rejection mechanism is less efficient, and the phase measured in the VH configuration presents a nearly linear drift from 0° to 3°. Also in this case, though, the cross-polarized scheme gives better results than the copolarized one, where the phase drift reaches the value of about 7° on the receiver edge (Figure 10(d)).
Similar results were obtained by using circularly polarized light (see Figure 11). For tap water ( ), the use of RR (copolarized) or RL (cross-polarized) detection configurations produces no significant differences (Figure 11(a)).
), the use of RR (copolarized) or RL (cross-polarized) detection configurations produces no significant differences (Figure 11(a)).
As turbidity increases, the copolarized scheme starts giving better results since-for an optically thin medium, that is, as long as single scattering events dominate-water reverses the helicity of circularly polarized incident light (Figure 11(b) and 11(c)) (this is strictly true in the absence of polarization memory effects (see below)).
As in the first experiment, a weak phase drift starts being observed also in the RR detection configuration when  (Figure 11(d)). This drift, though, is less marked than the corresponding effect observed for the VH scheme in the previous experiment (see Figure 12). In the hypothesis of spherical scattering particles, this discrepancy can be explained in terms of the different dependence of the
(Figure 11(d)). This drift, though, is less marked than the corresponding effect observed for the VH scheme in the previous experiment (see Figure 12). In the hypothesis of spherical scattering particles, this discrepancy can be explained in terms of the different dependence of the  and
and  elements of the normalized Mueller matrix on the scattering angle
elements of the normalized Mueller matrix on the scattering angle  in the range
in the range  [35]. In fact, linear polarization is strictly preserved (
[35]. In fact, linear polarization is strictly preserved ( ) only for
) only for  , and a partial degree of depolarization is permitted for scattering angles close to
, and a partial degree of depolarization is permitted for scattering angles close to  falling into the receiver field of view. The helicity flipping character of
falling into the receiver field of view. The helicity flipping character of  , on the other hand, is maintained over a wider angular range. Consequently, at fixed
, on the other hand, is maintained over a wider angular range. Consequently, at fixed  , the fraction of depolarized photons falling into the acceptance solid angle of the receiving optics is larger for linearly polarized incident light, and the combination (circularly polarized light + copolarized detection) is expected to give better results in terms of optical noise rejection.
, the fraction of depolarized photons falling into the acceptance solid angle of the receiving optics is larger for linearly polarized incident light, and the combination (circularly polarized light + copolarized detection) is expected to give better results in terms of optical noise rejection.
In multiple scattering regime ( ), the presence of large scatterers combined with the use of circularly polarized incident light would in principle allow for the observation of polarization memory effects, giving rise to a situation where the RL scheme better rejects optical noise than the RR one. However, in our case, no evidence of such a mechanism was found. Indeed, even the largest optical thickness considered in the experiments (
), the presence of large scatterers combined with the use of circularly polarized incident light would in principle allow for the observation of polarization memory effects, giving rise to a situation where the RL scheme better rejects optical noise than the RR one. However, in our case, no evidence of such a mechanism was found. Indeed, even the largest optical thickness considered in the experiments ( ) was still considerably less than the threshold value reported in the literature (
) was still considerably less than the threshold value reported in the literature ( ) for the observation of polarization memory effects [41, 42].
) for the observation of polarization memory effects [41, 42].
A second group of scans [43] were performed in similar conditions, but on a different target, namely a dark-gray-painted, sanded, metallic ladder. The ladder had 1 cm-high steps, apart from the first step whose height was 4 cm. In this case, we only used V-linearly polarized incident light, in combination with both copolarized (VV) and cross-polarized (VH) detection configurations. Two series of measurements were carried out by using, respectively: ( ) tap water (
) tap water ( ) and (
) and ( ) a mixture composed of tap water and skim milk (
) a mixture composed of tap water and skim milk ( ). In both cases the medium could be considered optically thin.
). In both cases the medium could be considered optically thin.
In each scan,  arrays of data were acquired by sweeping the laser probe (
arrays of data were acquired by sweeping the laser probe ( ) perpendicularly onto the target, with a sampling time per data element of 125 ms. Horizontal and vertical scanning angles were equal to 3.81° and 1.53°, respectively, corresponding to a scan area of 10 cm (length)
) perpendicularly onto the target, with a sampling time per data element of 125 ms. Horizontal and vertical scanning angles were equal to 3.81° and 1.53°, respectively, corresponding to a scan area of 10 cm (length)  4 cm (height).
4 cm (height).
The main results are reported in Figures 13 and 14. Specifically, Figure 13 shows an overplot of 40 linear phase profiles of the ladder. The theoretical phase differences, corresponding to the height of the ladder steps, can be calculated by means of the formula

obtained by inverting (1). So, for the first step ( ) one has
) one has  at 39 MHz, while for the others (
at 39 MHz, while for the others ( )
)  .
.
From Figure 13(a), it is clear that the phases measured in cross-polarized configuration and in clean water correspond fairly well to the expected values, thus permitting an accurate determination of the step heights, with an estimated uncertainty in the measurement of distance of 0.5 mm at 1.5 m.
A similar, yet slightly worse result was also obtained, always in clean water, in VV configuration (Figure 13(b)). This can be interpreted as an evidence that the scattering phenomenon has almost negligible effects on phase measurements in clean water, since the use of polarizers in cross—or copolarized working configuration does not significantly change the results.
The situation is completely different in the case of turbid water (Figure 13(c) and 13(d)). In fact, in conditions of higher scattering rates, the accuracy of phase measurements remains acceptable, and the structure of the ladder is still well distinguishable, only in VH detection configuration (Figure 13(c)), with an estimated uncertainty of 2 mm at 1.5 m.
On the contrary, a significant degradation is evident in the linear phase profiles obtained by using the copolarized scheme (Figure 13(d)), with distance uncertainty of 1 cm at 1.5 m.
Analogous results are shown in Figure 14, where 3D images of the ladder are reported. Specifically, 3D images recorded in the cross-polarized (VH) linear working scheme (Figure 14(a) and 14(c)) evidence better phase measurement accuracy, contrast, spatial resolution (of the order of millimeter at 1.5 m), as well as less phase noise compared to 3D models recorded by using the copolarized (VV) linear working configuration (Figure 14(b) and 14(d)). In the latter case, the steps look rougher and the ladder structure is smoothed due to the higher contribution of optical noise, especially for  .
.
In summary, also these results confirm that, at least for an optically thin medium, more effective optical noise rejection is achieved both in clean and turbid waters by using a cross-polarized (VH) rather than a copolarized (VV) detection scheme.
A last series of scans were finally performed on a white-painted, slightly bent metallic disc with diameter of 75 mm. The disc had a large hole in the center (diameter 33 mm), and four small holes equally spaced along the perimeter (diameter 4 mm). In this case, 0.1 ml of Maalox were added to 27 liters of tap water, in order to reproduce a turbid, optically thin, scattering medium, with all other experimental conditions left unchanged.
were added to 27 liters of tap water, in order to reproduce a turbid, optically thin, scattering medium, with all other experimental conditions left unchanged.
The scanned area, beside covering the entire disc, also included regions where only water was present, thus permitting a comparison of the contrast between target and the surrounding medium.
The results are shown in Figure 15, where two 3D images of the target are reported, each in two different orientations. The images were obtained in VV and VH configurations, respectively.
Underwater 3D images of a white-painted metallic disc with slightly curvature and some holes, immersed in turbid water (27 liters of tap water  0. 1 ml of Maalox
0. 1 ml of Maalox ) at a distance of 1.5 m from receiver, obtained by AMULOR system equipped with VH and VV linear polarizer configurations and working at fixed modulation frequency (
) at a distance of 1.5 m from receiver, obtained by AMULOR system equipped with VH and VV linear polarizer configurations and working at fixed modulation frequency ( ).
).
Also, in this case, it is possible to conclude that, for an optically thin medium and linearly polarized incident light, the use of a cross-polarized detection scheme enables one to improve the 3D imaging performances of the system, in terms of both phase and contrast.
In order to conclude the analysis of the experimental results presented in this section, it is worth noticing that the water cut-off frequency  , estimated by means of the theoretical model expounded in Section 3, was usually higher than the modulation frequency used in the experiments (
, estimated by means of the theoretical model expounded in Section 3, was usually higher than the modulation frequency used in the experiments ( ), especially for water of higher turbidity. As an example, the theoretical cut-off frequency corresponding to
), especially for water of higher turbidity. As an example, the theoretical cut-off frequency corresponding to  ,
,  ,
,  and
and  is
is  , and even higher values are obtained in more realistic conditions. So, it is possible to assert that the improvements observed in this case are actually due to the polarimetric technique and not to the low-pass filter behavior of the water backscattering frequency response.
, and even higher values are obtained in more realistic conditions. So, it is possible to assert that the improvements observed in this case are actually due to the polarimetric technique and not to the low-pass filter behavior of the water backscattering frequency response.
10. Conclusions
Beside confirming the soundness of the theoretical framework developed in the first part of this work, the experimental results presented in the last sections clearly illustrate the importance of optical noise rejection for underwater 3D imaging applications. Specifically, we showed that, in optically thin turbid water and in conditions of intermediate or quasi-Mie scattering regime, the contrast and phase accuracy of 3D images can be considerably improved by reducing the contribution of the optical noise, while this does not seem to be critical for clean water (Rayleigh scattering regime), at least for target distances within 3.7 m.
We demonstrated both theoretically and experimentally that, for underwater AM imagers that are only sensible to the modulated part of the received power, the signal due to the backscattering of light by the medium has a low-pass-filter dependence on the modulation frequency. The cut-off frequency is generally a complicated function of both the optical properties of the medium and the characteristics of the detection system, so it can be difficult, in practical situations, to identify an operational value for  that falls with certainty beyond the cut-off. Nonetheless, the results obtained give clear indications in favor of using the highest possible modulation frequency in any concrete situation.
that falls with certainty beyond the cut-off. Nonetheless, the results obtained give clear indications in favor of using the highest possible modulation frequency in any concrete situation.
We also showed that the oscillations in the amplitude  of the detected signal versus the laser modulation frequency originate from an interference-like effect between the target and water backscattering signals,
of the detected signal versus the laser modulation frequency originate from an interference-like effect between the target and water backscattering signals,  and
and  , respectively. In fact, oscillations only show up when the amplitudes
, respectively. In fact, oscillations only show up when the amplitudes  and
and  are comparable. Similar considerations apply to the contrast
are comparable. Similar considerations apply to the contrast  and signal-to-optical-noise ratio
and signal-to-optical-noise ratio  , directly related to the accuracy of the 3D imaging data. All these quantities are characterized by regularly spaced minima and maxima, depending on the attenuation coefficient and the target-receiver distance. We showed that
, directly related to the accuracy of the 3D imaging data. All these quantities are characterized by regularly spaced minima and maxima, depending on the attenuation coefficient and the target-receiver distance. We showed that  and
and  can be significantly increased by choosing working modulation frequencies higher than the system-specific cut-off frequency
can be significantly increased by choosing working modulation frequencies higher than the system-specific cut-off frequency  —where oscillations tend to disappear, owing to the low-pass filter behavior of water backscattering frequency response. Improvements, though, can be obtained even for frequencies lower than
—where oscillations tend to disappear, owing to the low-pass filter behavior of water backscattering frequency response. Improvements, though, can be obtained even for frequencies lower than  , provided they correspond to local maxima of
, provided they correspond to local maxima of  and
and  . Since the determination of the maxima can be unpractical in most concrete situations, a valid alternative consists in subtracting from the detected signal the optical noise measured independently by shooting the laser beam in open water. Indeed, we proved that the oscillations of
. Since the determination of the maxima can be unpractical in most concrete situations, a valid alternative consists in subtracting from the detected signal the optical noise measured independently by shooting the laser beam in open water. Indeed, we proved that the oscillations of  and
and  can be almost completely removed by direct cancellation of the optical noise, provided the target is not too close to the detector, since in that case the optical noise component of the signal could be overestimated by the backscattering measured in open water.
can be almost completely removed by direct cancellation of the optical noise, provided the target is not too close to the detector, since in that case the optical noise component of the signal could be overestimated by the backscattering measured in open water.
A sensible reduction of the optical noise can also be achieved by using polarization-sensitive detection. The technique is based on the distinct polarization properties of radiation backscattered off water and by the target, respectively. Polarization control on both the transmitter and receiver stages is obtained by means of appropriate polarizer combinations (copolarized or cross-polarized schemes).
We showed that, for linearly polarized light propagating in an optically thin medium, where polarization memory effects don't occur, the cross-polarized (VH) scheme permits to obtain a better optical noise rejection. The opposite occurs for circularly polarized radiation, where the copolarized (RR) scheme is more effective in the filtering out the optical noise. We also showed that, if water turbidity increases up to degrees where multiple scattering events start playing a role-but polarization memory effects are still negligible—, the use of circularly polarized light in combination with a copolarized detection scheme provides slightly better results than the cross-polarized configuration based on linear polarization.
However, the use of polarizers in the transmitter and receiver stages can strongly limit the operating range of the system, since only a part of the target signal is revealed, with a consequent reduction of the signal-to-noise ratio. The attenuation of the signal can be significant even for targets relatively close to the receiver, depending on the water optical properties and on the depolarizing characteristics of the target. So, modulation/demodulation techniques, such as those discussed in Sections 7 and 8, are to be preferred in case of weak detected signals.
References
Kocak DM, Dalgleish FR, Caimi FM, Schechner YY: A focus on recent developments and trends in underwater imaging. Marine Technology Society Journal 2008, 42(1):52-67. 10.4031/002533208786861209
Mullen L, Laux A, Concannon B, Zege EP, Katsev IL, Prikhach AS: Amplitude-modulated laser imager. Applied Optics 2004, 43(19):3874-3892. 10.1364/AO.43.003874
Bartolini L, De Dominicis L, Ferri de Collibus M, et al.: Underwater three-dimensional imaging with an amplitude-modulated laser radar at a 405 nm wavelength. Applied Optics 2005, 44(33):7130-7135. 10.1364/AO.44.007130
Sogandares FM, Fry ES: Absorption spectrum (340–640 nm) of pure water. I. Photothermal measurements. Applied Optics 1997, 36(33):8699-8709. 10.1364/AO.36.008699
Pope RM, Fry ES: Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Applied Optics 1997, 36(33):8710-8723. 10.1364/AO.36.008710
Strand P: Underwater electro-optical system for mine identification. Detection Technologies for Mines and Minelike Targets, 1995, Proceedings of SPIE 2496: 487-497.
Mullen L, Vieira AJC, Herczfeld PR, Contarino VM: Application of RADAR technology to aerial LIDAR systems for enhancement of shallow underwater target detection. IEEE Transactions on Microwave Theory and Techniques 1995, 43(9):2370-2377. 10.1109/22.414591
Pellen F, Intes X, Olivard P, Guern Y, Cariou J, Lotrian J: Determination of sea-water cut-off frequency by backscattering transfer function measurement. Journal of Physics D 2000, 33(4):349-354. 10.1088/0022-3727/33/4/306
Pellen F, Olivard P, Guern Y, Cariou J, Lotrian J: Radio frequency modulation on an optical carrier for target detection enhancement in sea-water. Journal of Physics D 2001, 34(7):1122-1130. 10.1088/0022-3727/34/7/315
Mullen LJ, Laux AE, Cochenour B, Zege EP: FAMIS (Frequency Agile Modulated Imaging System) sensor for imaging in turbid water. Photonics for Port and Harbor Security II, 2006, Proceedings of SPIE 6204: 1-13. 62040E
Mullen L, Laux A, Cochenour B, Zege EP, Katsev IL, Prikhach AS: Demodulation techniques for the amplitude modulated laser imager. Applied Optics 2007, 46(30):7374-7383. 10.1364/AO.46.007374
Bartolini L, De Dominicis L, Ferri de Collibus M, et al.: Experimental evidence of signal-optical noise interferencelike effect in underwater amplitude-modulated laser optical radar systems. Optics Letters 2008, 33(22):2584-2586. 10.1364/OL.33.002584
Bartolini L, De Dominicis L, Fornetti G, et al.: Improvement in underwater phase measurement of an amplitude-modulated laser beam by polarimetric techniques. Optics Letters 2007, 32(11):1402-1404. 10.1364/OL.32.001402
Zege EP, Ivanov AP, Katsev IL: Image Transfer Through a Scattering Medium. Springer, Heidelberg, Germany; 1991.
Kim AD, Moscoso M: Influence of the relative index on the depolarization of multiply scattered waves. Physical Review E 2001, 64(2) Article ID 026612,:-5.
Zege EP, Katsev IL, Polonsky IN: Multicomponent approach to light propagation in clouds and mists. Applied Optics 1993, 32(15):2803-2812. 10.1364/AO.32.002803
Mullen LJ, Zege EP, Katsev IL, Prikhach AS: Modulated lidar system: experiment vs. theory. Ocean Optics: Remote Sensing and Underwater Imaging, 2002, Proceedings of SPIE 4488: 25-35.
Arnush D: Underwater light-beam propagation in the small-angle-scattering approximation. Journal of the Optical Society of America 1972, 62(9):1109-1111. 10.1364/JOSA.62.001109
Katsev IL, Zege EP, Prikhach AS, Polonsky IN: Efficient technique to determine backscattered light power for various atmospheric and oceanic sounding and imaging systems. Journal of the Optical Society of America A 1997, 14(6):1338-1346. 10.1364/JOSAA.14.001338
Bissonnette LR: Lidar and multiple scattering. In Lidar Range-Resolved Optical Remote Sensing of the Atmosphere. Edited by: Weitkamp C. Springer, New York, NY, USA; 2005:43-104.
Hogan RJ: Fast lidar and radar multiple-scattering models—part I: small-angle scattering using the photon variance-covariance method. Journal of the Atmospheric Sciences 2008, 65(12):3621-3635. 10.1175/2008JAS2642.1
Gilbert GD, Pernicka JC: Improvement of underwater visibility by reduction of backscatter with a circular polarization technique. Applied Optics 1967, 6(4):741-746. 10.1364/AO.6.000741
Gilbert GD: The effects of particle size on contrast improvement by polarization discrimination for underwater targets. Applied Optics 1970, 9(2):421-428. 10.1364/AO.9.000421
Cariou J, Le Jeune B, Lotrian J, Guern Y: Polarization effects of seawater and underwater targets. Applied Optics 1990, 29(11):1689-1695. 10.1364/AO.29.001689
Le Brun G, Le Jeune B, Cariou J, Lotrian J: Laser imaging procedure for evaluating the polarization signature of immersed targets. Pure and Applied Optics 1993, 2(5):455-470. 10.1088/0963-9659/2/5/007
Bartolini L, De Dominicis L, Ferri de Collibus M, et al.: Polarimetry as tool to improve phase measurement in an amplitude modulated laser for submarine archaeological sites inspection. O3A: Optics for Arts, Architecture, and Archaeology, 2007, Proceedings of SPIE 6618: 66180I
Nothdurft RE, Yao G: Effects of turbid media optical properties on object visibility in subsurface polarization imaging. Applied Optics 2006, 45(22):5532-5541. 10.1364/AO.45.005532
Baba JS, Chung J-R, DeLaughter AH, Cameron BD, Coté GL: Development and calibration of an automated Mueller matrix polarization imaging system. Journal of Biomedical Optics 2002, 7(3):341-349. 10.1117/1.1486248
van de Hulst HC: Light Scattering by Small Particles. Dover, New York, NY, USA; 1981.
Kattawar GW, Raković MJ: Virtues of Mueller matrix imaging for underwater target detection. Applied Optics 1999, 38(30):6431-6438. 10.1364/AO.38.006431
Singham SB, Salzman GC: Evaluation of the scattering matrix of an arbitrary particle using the coupled dipole approximation. The Journal of Chemical Physics 1986, 84(5):2658-2667. 10.1063/1.450338
Crofcheck CL, Payne FA, Mengüç MP: Characterization of milk properties with a radiative transfer model. Applied Optics 2002, 41(10):2028-2037. 10.1364/AO.41.002028
Kouzoubov A, Brennan MJ, Thomas JC: Treatment of polarization in laser remote sensing of ocean water. Applied Optics 1998, 37(18):3873-3885. 10.1364/AO.37.003873
Raković MJ, Kattawar GW, Mehrűbeoğlu M, et al.: Light backscattering polarization patterns from turbid media: theory and experiment. Applied Optics 1999, 38(15):3399-3408. 10.1364/AO.38.003399
Crofcheck C, Wade J, Swamy JN, Aslan MM, Mengüç MP: Effect of fat and casein particles in milk on the scattering of elliptically polarized light. Transactions of the American Society of Agricultural Engineers 2005, 48(3):1147-1155.
MacKintosh FC, Zhu JX, Pine DJ, Weitz DA: Polarization memory of multiply scattered light. Physical Review B 1989, 40(13):9342-9345. 10.1103/PhysRevB.40.9342
Toublanc D: Henyey-Greenstein and Mie phase functions in Monte Carlo radiative transfer computations. Applied Optics 1996, 35(18):3270-3274. 10.1364/AO.35.003270
Berrocal E, Sedarsky DL, Paciaroni ME, Meglinski IV, Linne MA: Laser light scattering in turbid media—part I: experimental and simulated results for the spatial intensity distribution. Optics Express 2007, 15(17):10649-10665. 10.1364/OE.15.010649
Kerker M: The Scattering of Light and Other Electromagnetic Radiation. Academic Press, New York, NY, USA; 1969.
Bicout D, Brosseau C, Martinez AS, Schmitt JM: Depolarization of multiply scattered waves by spherical diffusers: influence of the size parameter. Physical Review E 1994, 49(2):1767-1770. 10.1103/PhysRevE.49.1767
Ni X, Alfano RR: Time-resolved backscattering of circularly and linearly polarized light in a turbid medium. Optics Letters 2004, 29(23):2773-2775. 10.1364/OL.29.002773
Kim AD, Moscoso M: Backscattering of circularly polarized pulses. Optics Letters 2002, 27(18):1589-1591. 10.1364/OL.27.001589
De Dominicis L, Ferri de Collibus M, Fornetti G, et al.: Polarimetry as a valid means to reduce optical noise in underwater 3D imagine by means of amplitude-modulated laser optical radar systems. Optics Letters 2009, 34(14):2117-2119. 10.1364/OL.34.002117
Acknowledgments
We acknowledge Drs. M. Sighicelli, A. Lai, and C. Poggi for the contribution given at this work, funded in the framework of the national project "BLU-Archeosys-Diagnostica per l'archeologia subacquea" (Diagnostics for underwater archaeology).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ricci, R., Francucci, M., De Dominicis, L. et al. Techniques for Effective Optical Noise Rejection in Amplitude-Modulated Laser Optical Radars for Underwater Three-Dimensional Imaging. EURASIP J. Adv. Signal Process. 2010, 958360 (2010). https://doi.org/10.1155/2010/958360
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/958360
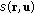 and
and 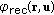 , and calculate
, and calculate
 , and calculate its Fourier transform
, and calculate its Fourier transform 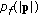 ;
;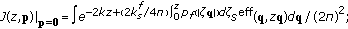
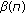 and eventually calculate
and eventually calculate

 for
for
 and
and
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 , due to the overlapping between target and water signals (see Section 4);
, due to the overlapping between target and water signals (see Section 4);

 for
for  . Filled squares represent the experimental measures. The other curves were obtained by means of the theoretical model with
. Filled squares represent the experimental measures. The other curves were obtained by means of the theoretical model with  ,
,  ,
,  and the following values for the other parameters: (1)
and the following values for the other parameters: (1)  ,
,  (dashed line); (2)
(dashed line); (2)  ,
,  ,
,  (solid line).
(solid line).
 for
for  . Filled squares represent the experimental measures. The other curves were obtained by means of the theoretical model with
. Filled squares represent the experimental measures. The other curves were obtained by means of the theoretical model with  ,
,  ,
,  and the following values for the other parameters: (1)
and the following values for the other parameters: (1)  ,
,  (dashed line); (2)
(dashed line); (2)  ,
,  ,
,  (solid line).
(solid line).
 . Note that the ladder is shown with various orientations.
. Note that the ladder is shown with various orientations.
 ) at a distance of 3. 7 m from receiver obtained by AMULOR working at
) at a distance of 3. 7 m from receiver obtained by AMULOR working at  .
. and
and 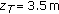 (
( on average),
on average), and
and 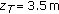 (
(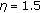 on average),
on average),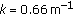 and
and 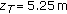 (
(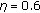 on average).
on average).
 and
and  (a. u.) versus
(a. u.) versus  for (1)
for (1)  ,
,  ,
,  ,
,  (a); (2)
(a); (2)  ,
,  ,
,  ,
,  (b); (3)
(b); (3)  ,
,  ,
,  ,
,  (c).
(c).
 and
and  versus
versus  for (1)
for (1)  ,
,  ,
,  ,
,  (a); (2)
(a); (2)  ,
,  ,
,  ,
,  (b); (3)
(b); (3)  ,
,  ,
,  ,
,  (c). Note the general growing tendency of
(c). Note the general growing tendency of  and
and  for increasing
for increasing  .
.
 and
and  versus
versus  for(1)
for(1)  ,
,  ,
,  ,
,  (a); (2)
(a); (2)  ,
,  ,
,  ,
,  (b);(3)
(b);(3)  ,
,  ,
,  ,
,  (c). Note the general growing tendency of
(c). Note the general growing tendency of  and
and  for increasing
for increasing  .
.
 ) corresponding to VV (filled circles) and VH (open circles) schemes, for water of various turbidity levels. The AM laser beam (
) corresponding to VV (filled circles) and VH (open circles) schemes, for water of various turbidity levels. The AM laser beam ( ) was linearly polarized perpendicularly to the reference plane (vertical linear polarization).
) was linearly polarized perpendicularly to the reference plane (vertical linear polarization).
 ) corresponding to RL (filled circles) and RR (open circles) schemes, for water of various turbidity levels. The AM laser beam (
) corresponding to RL (filled circles) and RR (open circles) schemes, for water of various turbidity levels. The AM laser beam ( ) was in right-handed circular polarization state.
) was in right-handed circular polarization state.
 ,
,
 ).
).


