- Research Article
- Open access
- Published:
FPGA Implementation of the Pixel Purity Index Algorithm for Remotely Sensed Hyperspectral Image Analysis
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 969806 (2010)
Abstract
Hyperspectral imaging is a new emerging technology in remote sensing which generates hundreds of images, at different wavelength channels, for the same area on the surface of the Earth. Over the last years, many algorithms have been developed with the purpose of finding endmembers, assumed to be pure spectral signatures in remotely sensed hyperspectral data sets. One of the most popular techniques has been the pixel purity index (PPI). This algorithm is very time-consuming. The reconfigurability, compact size, and high computational power of Field programmable gate arrays (FPGAs) make them particularly attractive for exploitation in remote sensing applications with (near) real-time requirements. In this paper, we present an FPGA design for implementation of the PPI algorithm. Our systolic array design includes a DMA and implements a prefetching technique to reduce the penalties due to the I/O communications. We have also included a hardware module for random number generation. The proposed method has been tested using real hyperspectral data collected by NASA's Airborne Visible Infrared Imaging Spectrometer over the Cuprite mining district in Nevada. Experimental results reveal that the proposed hardware system is easily scalable and able to provide accurate results with compact size in (near) real-time, which make our reconfigurable system appealing for on-board hyperspectral data processing.
1. Introduction
Hyperspectral imaging is concerned with the measurement, analysis, and interpretation of spectra acquired from a given scene (or specific object) at a short, medium, or long distance by an airborne or satellite sensor [1]. The concept of hyperspectral imaging originated at NASA's Jet Propulsion Laboratory in California, which developed instruments such as the Airborne Imaging Spectrometer (AIS), then called AVIRIS, for Airborne Visible Infrared Imaging Spectrometer [2]. This system is now able to cover the wavelength region from 0.4 to 2.5  m using more than two hundred spectral channels, at nominal spectral resolution of 10 nm. As a result, each pixel (considered as a vector) collected by a hyperspectral instrument can be seen as a spectral signature or fingerprint of the underlying materials within the pixel (see Figure 1).
m using more than two hundred spectral channels, at nominal spectral resolution of 10 nm. As a result, each pixel (considered as a vector) collected by a hyperspectral instrument can be seen as a spectral signature or fingerprint of the underlying materials within the pixel (see Figure 1).
Several analytical tools have been developed for hyperspectral data processing in recent years, covering topics like dimensionality reduction, classification, data compression, or spectral mixture analysis [3]. The underlying assumption governing clustering and classification techniques is that each pixel vector comprises the response of a single underlying material. However, if the spatial resolution of the sensor is not high enough to separate different materials, these can jointly occupy a single pixel and the resulting spectral measurement will be a mixed pixel, that is, a composite of the individual pure spectra. For instance, in Figure 1 it is likely that the pixel labeled as "vegetation" is actually a mixture of vegetation and soil, or of different types of vegetation canopies.
To deal with this problem, linear spectral mixture analysis techniques [4] first identify a collection of spectrally pure constituent spectra, called endmembers in hyperspectral analysis terminology [5] and then express the measured spectrum of each mixed pixel as a linear combination of endmembers weighted by fractions or abundances that indicate the proportion of each endmember present in the pixel. In fact, spectral mixture analysis has been an alluring exploitation goal since the earliest days of hyperspectral imaging [4]. No matter the spatial resolution, in natural environments the spectral signature for a nominal pixel is invariably a mixture of the signatures of the various materials found within the spatial extent of the ground instantaneous field view of the sensor. In hyperspectral imagery, the number of spectral bands usually exceeds the number of pure spectral components and the unmixing problem is cast in terms of an overdetermined system of equations in which given the correct set of endmembers allows determination of the actual endmember abundance fractions through a numerical inversion process.
Let us assume that a remotely sensed hyperspectral scene with  bands is denoted by
bands is denoted by  , in which a pixel at discrete spatial coordinates is represented by a vector
, in which a pixel at discrete spatial coordinates is represented by a vector  , where
, where  denotes the spectral response at the
denotes the spectral response at the  th wavelength, with
th wavelength, with  . Under the linear mixture model assumption, each pixel vector in the original scene can be modeled using the following expression:
. Under the linear mixture model assumption, each pixel vector in the original scene can be modeled using the following expression:

where  designates the
designates the  th pure spectral component (endmember) residing in the pixel,
th pure spectral component (endmember) residing in the pixel,  is a scalar value designating the fractional abundance of the endmember
is a scalar value designating the fractional abundance of the endmember  at the pixel
at the pixel  ,
,  is the total number of endmembers, and
is the total number of endmembers, and  is a noise vector. The solution of the linear spectral mixture problem described in (1) relies on the correct determination of a set
is a noise vector. The solution of the linear spectral mixture problem described in (1) relies on the correct determination of a set  of endmembers. It is such derivation and validation of the correct suite of endmembers that has remained a challenging goal for the past years (not only in terms of adequate spectral signature extraction, but also in terms of computational complexity [6]).
of endmembers. It is such derivation and validation of the correct suite of endmembers that has remained a challenging goal for the past years (not only in terms of adequate spectral signature extraction, but also in terms of computational complexity [6]).
The pixel purity index (PPI) algorithm [7] has been widely used in hyperspectral image analysis for endmember extraction due to its publicity and availability in ITTVIS (http://www.ittvis.com/) Environment for Visualizing Images (ENVIs) software originally developed by Analytical Imaging and Geophysics (AIGs) [8]. The algorithm searches for a set of vertices of a convex hull in a given dataset, which are supposed to be pure signatures present in the data. Due to its propriety and limited published results, its detailed implementation has never been made publicly available. Therefore, most of the people who use the PPI for endmember extraction either appeal for ENVI software or implement their own versions of the PPI based on whatever available in the literature. The general procedure of the PPI algorithm can be summarized as follows [9].
-
(1)
First, a pixel purity score is calculated for each pixel vector
 in the input hyperspectral image cube
in the input hyperspectral image cube 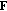 by generating
by generating  random,
random,  -dimensional vectors, called skewers.
-dimensional vectors, called skewers. -
(2)
Then, each pixel vector
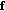 in the input data is projected onto the entire set of skewers
in the input data is projected onto the entire set of skewers  , and the pixels falling at the extremes of each skewer are tallied (see Figure 2). After many repeated projections to different random skewers, those pixels which are repeatedly selected during the process are identified and placed on a list of endmember candidates.
, and the pixels falling at the extremes of each skewer are tallied (see Figure 2). After many repeated projections to different random skewers, those pixels which are repeatedly selected during the process are identified and placed on a list of endmember candidates. -
(3)
The potential endmember spectra are then loaded into an interactive tool (such as ENVI's
 -dimensional visualizer, available as a built-in companion piece in ENVI software) and rotated until a desired number of endmembers are visually identified as extreme pixels in the data cloud.
-dimensional visualizer, available as a built-in companion piece in ENVI software) and rotated until a desired number of endmembers are visually identified as extreme pixels in the data cloud.
The PPI algorithm suffers from several limitations [10]. First and foremost, the algorithm is sensitive to parameter  , that is, the number of skewers. Since the skewers are randomly generated, a large number of skewer projections are generally required in order to arrive to satisfactory endmember sets in terms of signature purity. The authors recommend using as many random skewers as possible in order to obtain optimal results [7]. As a result, the PPI can only guarantee to produce optimal results asymptotically and its computational complexity is very high, thus requiring efficient implementations. Another shortcoming of the PPI is the fact that an interactive tool is needed to perform the final endmember selection. An alternative is to retain the pixels that have been selected above a predefined threshold and then automatically remove spectrally redundant endmembers [10]. This is generally treated as a postprocessing stage external to the algorithm.
, that is, the number of skewers. Since the skewers are randomly generated, a large number of skewer projections are generally required in order to arrive to satisfactory endmember sets in terms of signature purity. The authors recommend using as many random skewers as possible in order to obtain optimal results [7]. As a result, the PPI can only guarantee to produce optimal results asymptotically and its computational complexity is very high, thus requiring efficient implementations. Another shortcoming of the PPI is the fact that an interactive tool is needed to perform the final endmember selection. An alternative is to retain the pixels that have been selected above a predefined threshold and then automatically remove spectrally redundant endmembers [10]. This is generally treated as a postprocessing stage external to the algorithm.
An exciting new development in the field of specialized commodity computing for accelerating computationally intensive algorithms is the emergence of hardware devices such as field programmable gate arrays (FPGAs) [11–13], which can bridge the gap towards on-board and real-time analysis of remote sensing data [14, 15]. FPGAs are now fully reconfigurable [16, 17], a technological feature that, in our application context, allows a control station on Earth to adaptively select a data processing algorithm (out of a pool of available algorithms implemented on the FPGA) to be applied on board the sensor. The ever-growing computational demands of hyperspectral imaging applications can fully benefit from compact, reconfigurable hardware components and take advantage of the small size and relatively low cost of these units.
In this paper, we develop an FPGA-based hardware version of the PPI algorithm. The proposed implementation is aimed at enhancing code reusability and efficient implementation in FPGA devices through the utilization of systolic array design. One of the main advantages of systolic array-based implementations is that they are able to provide a systematic procedure for system design that allows for the derivation of a well-defined processing element-based structure and an interconnection pattern which can then be easily ported to real hardware configurations. The remainder of the paper is organized as follows. Section 2 discusses the role of reconfigurable hardware in remote sensing missions. Section 3 describes our implementation of the PPI algorithm. Section 4 describes its parallel implementation on a Xilinx Virtex-II PRO xc2vp30 FPGA. Section 5 provides an experimental assessment of both endmember extraction accuracy and parallel processing performance of the proposed FPGA-based algorithm, using a well-known hyperspectral data set (with quality ground-truth) collected by the NASA Jet Propulsion Laboratory's Airborne Visible Infrared Imaging Spectrometer (AVIRIS) [2] over the Cuprite mining district in Nevada. Finally, Section 6 concludes with some remarks and hints at plausible future research lines.
2. The Role of Reconfigurable Hardware in Remote Sensing Missions
The trend in remote sensing missions has always been towards using hardware devices with smaller size, lower cost, more flexibility, and higher computational power [18, 19]. On-board processing, as a solution, allows for a good reutilization of expensive hardware resources. Instead of storing and forwarding all captured images, remote sensing data interpretation can be performed on orbit prior to downlink, resulting in a significant reduction of communication bandwidth as well as simpler and faster subsequent computations to be performed at ground stations. In this regard, FPGAs combine the flexibility of traditional microprocessors with the power and performance of application-specific integrated circuits (ASICs). Therefore, FPGAs are a promising candidate for on-board remote sensing data processing.
Figure 3 illustrates some potential advantages of using reconfigurable hardware in remote sensing data processing. The transmission of high-dimensional information collected by a satellite-based instrument to a control station on Earth for subsequent processing may turn into a very slow task, mainly due to the reduced bandwidth available and to the fact that the connection may be restricted to a short period of time. The ability to interpret remote sensing data on-board can significantly reduce the amount of bandwidth and storage space needed in the generation of science products. Subsequently, on-board processing has the potential to reduce the cost and the complexity of ground control systems. Furthermore, it allows autonomous decisions (to be taken on board) that can potentially reduce the delay between image capture, analysis, and action.
Recently, FPGAs have become a viable target technology for implementation of remotely sensed hyperspectral imaging algorithms [20]. These computing systems combine the flexibility of general purpose processors with the speed of application-specific processors. Reconfigurable hardware offers the necessary flexibility and performance with reduced energy consumption compared to other high performance processors. By mapping functionality to FPGAs, the computer designer can optimize the hardware for a specific application resulting in acceleration rates of several orders of magnitude over general-purpose computers. In addition, these devices are characterized by lower form/wrap factors compared to parallel platforms and by higher flexibility than ASIC solutions. Reconfigurable computing technology further allows new hardware circuits to be uploaded via a radio link for physical upgrade or repair [21].
Moreover, satellite-based remote sensing instruments can only include chips that had been certified for space conditions. This is because space-based systems must operate in an environment in which radiation effects have an adverse impact on integrated circuit operation [22]. Ionizing radiation can cause soft-errors in the static cells used to hold the configuration data. This will affect the circuit functionality and can cause system failure. So it requires special FPGAs that provide on-chip reconfiguration error-detection and/or correction circuitry. High-speed, radiation-hardened FPGA chips with million gate densities have recently emerged that can support the high throughput requirements for the remote sensing applications. Radiation-hardened FPGAs are in great demand for military and space applications. For instance, industrial partners such as Actel Corporation (http://www.actel.com/) or Xilinx (http://www.xilinx.com/) have been producing radiation-tolerant antifuse FPGAs for several years for high-reliability space-flight systems. Actel FPGAs have been on board more than 100 launches and Xilinx FPGAs have been used in more than 50 missions [22]. In this work, we use a Xilinx Virtex-II PRO xc2vp30 FPGA as a baseline architecture because it is similar to other FPGAs [23] that have been certified by several international agencies for remote sensing applications. They are based on the same architecture so we could immediately implement our design on them.
3. The Pixel Purity Index (PPI) Algorithm
Since the details of the specific steps to implement ENVI's PPI are not available in the literature, the PPI algorithm described below is only based on the limited published results and our own interpretation [10]. Nevertheless, except a final manual supervision step (included in ENVI's PPI) which is replaced by step 4, both our approximation and the PPI in ENVI 4.0 produce very similar results. The inputs to the algorithm are a hyperspectral data cube F with  dimensions; the number of random skewers to be generated during the process, K; and a cut-off threshold value,
dimensions; the number of random skewers to be generated during the process, K; and a cut-off threshold value,  , used to select as final endmembers only those pixels that have been selected as extreme pixels at least
, used to select as final endmembers only those pixels that have been selected as extreme pixels at least  times throughout the PPI process.
times throughout the PPI process.
The algorithm is given by the following steps.
-
(1)
Skewer generation. Produce a set of K randomly generated unit vectors
 .
. -
(2)
Extreme projections. For each
 ,
, 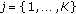 , all pixel vectors
, all pixel vectors 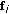 in the original data set F are projected onto
in the original data set F are projected onto  via dot products of
via dot products of  to find sample vectors at its extreme (maximum and minimum) projections, thus forming an extrema set for
to find sample vectors at its extreme (maximum and minimum) projections, thus forming an extrema set for 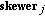 which is denoted by
which is denoted by 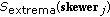 . Despite the fact that different skewers generate different extrema sets, it is very likely that some sample vectors may appear in more than one extrema set. To account for this, we define an indicator function of a set F, denoted by
. Despite the fact that different skewers generate different extrema sets, it is very likely that some sample vectors may appear in more than one extrema set. To account for this, we define an indicator function of a set F, denoted by  , to denote membership of an element x to that particular set as follows:
, to denote membership of an element x to that particular set as follows: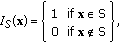 (2)
(2) -
(3)
Calculation of PPI scores. Using the indicator function above, we calculate the PPI score associated to each pixel vector
 (i.e., the number of times that a given pixel has been selected as extreme in step 2) using the following equation:
(i.e., the number of times that a given pixel has been selected as extreme in step 2) using the following equation: (3)
(3) -
(4)
Endmember selection. Find the pixel vectors with scores of
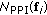 which are above
which are above  and label them as spectral endmembers. An optional postprocessing (not implemented in this work) based on removing potentially redundant endmembers may be also applied.
and label them as spectral endmembers. An optional postprocessing (not implemented in this work) based on removing potentially redundant endmembers may be also applied.
The most time-consuming stage of the PPI algorithm is stage 2 (extreme projections). For example, running this stage on a hyperspectral image with  pixels (the standard number of pixels produced by NASA's AVIRIS instrument in a single frame, each with 224 spectral bands) using
pixels (the standard number of pixels produced by NASA's AVIRIS instrument in a single frame, each with 224 spectral bands) using  skewers requires the calculation of more than
skewers requires the calculation of more than  multiplication/accumulation (MAC) operations, that is, a few hours of nonstop computation on a 500 MHz microprocessor with 256 Mbytes SDRAM [24, 25]. In [20], another example is reported in which the PPI algorithm available in ENVI 4.0 version took more than 50 minutes of computation to project every data sample vector of a hyperspectral image with the same size reported above onto
multiplication/accumulation (MAC) operations, that is, a few hours of nonstop computation on a 500 MHz microprocessor with 256 Mbytes SDRAM [24, 25]. In [20], another example is reported in which the PPI algorithm available in ENVI 4.0 version took more than 50 minutes of computation to project every data sample vector of a hyperspectral image with the same size reported above onto  skewers in a PC with AMD Athlon 2.6 GHz processor and 512 MB of RAM.
skewers in a PC with AMD Athlon 2.6 GHz processor and 512 MB of RAM.
Fortunately, the PPI algorithm is well suited for parallel implementation. The computation of skewer projections is independent and can be performed simultaneously, leading to many ways of parallelization. In [24, 25], two parallel architectures for implementation of the PPI are proposed. Both are based on a 2D processor array tightly connected to a few memory banks. A speedup of 80 is obtained through an FPGA implementation on the Wildforce board (4 Xilinx XC4036EX plus 4 memory banks of 512 Kbytes) [26]. As a matter of fact, this design is tailored to the Wildforce board and it cannot be reused for another board without huge modifications. In [10], a fast iterative PPI (FPPI) is introduced. The Matlab-based software implementation of the FPPI algorithm was more than 24 times faster than the ENVI's PPI algorithm in the same computing environment, while the FPGA-based implementation showed a significant increase in performance with regards to the two considered software versions due to the low-level hardware implementation. Although these works have demonstrated the efficiency of a hardware implementation on a reconfigurable board, these solutions are not scalable.
The FPGA implementation that we present in the following section aims at overcoming these drawbacks. First, our architecture specification can be easily adapted to different platforms. Second, our proposed architecture is scalable depending on the amount of available resources because the required resources grow proportionally with the number of skewers and the clock cycle remains constant.
4. FPGA Implementation
4.1. Parallel Design Strategies for the PPI Algorithm
The most time-consuming stage (extreme projections) of the PPI computes a very large number of dot products, all of which can be performed simultaneously. If we consider a simple dot-product unit such as the one displayed in Figure 4(a) as the baseline for parallel computations, then we can perform the parallel computations by pixels (see Figure 4(b)), by skewers (see Figure 4(c)), or by pixels and skewers (see Figure 4(d)). If we parallelize the computations by pixels, additional hardware is necessary to compare all the maxima and minima between them. As we increase the number of parallel computations, a greater area would be required for maxima/minima computations and the critical path would be longer, hence, the clock cycle would be higher. Another possible way to parallelize the extreme projections stage is to compute  dot products at the same time for the same pixel, where
dot products at the same time for the same pixel, where  is the number of skewers (see Figure 4(c)). If we increase the number of skewers in this case, the required area would grow proportionally with the number of dot-product units and the clock cycle would remain constant. Finally, the parallelization strategy in Figure 4(d) is a mixed solution which provides no further advantage with respect to the parallelization by skewers and has the same problems that parallelization by pixels has.
is the number of skewers (see Figure 4(c)). If we increase the number of skewers in this case, the required area would grow proportionally with the number of dot-product units and the clock cycle would remain constant. Finally, the parallelization strategy in Figure 4(d) is a mixed solution which provides no further advantage with respect to the parallelization by skewers and has the same problems that parallelization by pixels has.
Taking in mind the above rationale, in this work we have selected the parallelization strategy based on skewers. Apart from the aforementioned advantages with regard to other possible strategies, another reason for this selection is that the parallelization strategy based on skewers fits very well how the image data reaches the system. In our case, our goal is to make an on-line processing of the hyperspectral images bearing in mind that hyperspectral sensors capture the image data in a pixel by pixel fashion. Therefore, parallelization by skewers is the one that best fits the data entry mechanism since each pixel can be processed immediately as collected. Specifically, our hardware system should be able to compute  dot products at the same time against the same pixel
dot products at the same time against the same pixel  , where
, where  is the number of skewers. In such a system, the extreme projections step of the PPI (the most time-consuming one in the PPI process) can be simply written as described in Algorithm 1.
is the number of skewers. In such a system, the extreme projections step of the PPI (the most time-consuming one in the PPI process) can be simply written as described in Algorithm 1.
Algorithm 1: Parallel implementation of extreme projections step.
for ( ;
;  ;
;  ++)
++) //
// denotes the number of pixels
denotes the number of pixels
par ( ;
;  ;
;  ++)
++) //
// denotes the number of skewers
denotes the number of skewers
dp =dot_product(pixels
=dot_product(pixels ,skewers
,skewers );
);
if (dp
 Min
Min )
)  Min
Min =dp
=dp ; Reg_Min
; Reg_Min =
= ;
;
if (dp
 Max
Max )
)  Max
Max =dp
=dp ; Reg_Max
; Reg_Max =
= ;
;
 end par
end par
 end for
end for
The par loop in Algorithm 1 expresses that  dot products are first performed in parallel, then
dot products are first performed in parallel, then  Min and Max operations are also computed in parallel. Now, if we suppose that we cannot simultaneously compute
Min and Max operations are also computed in parallel. Now, if we suppose that we cannot simultaneously compute  dot products but only a fraction
dot products but only a fraction  , where
, where  is the number of available processing units in the underlying parallel platform, then the extreme projections step can be split into
is the number of available processing units in the underlying parallel platform, then the extreme projections step can be split into  passes, each performing
passes, each performing  dot products, as indicated in Algorithm 2. From an architectural point of view, each processor receives successively the
dot products, as indicated in Algorithm 2. From an architectural point of view, each processor receives successively the  pixels, computes
pixels, computes  dot-products, and keeps in memory the Min and the Max dot products. In this scheme, each processor holds a different skewer which must be input before each new pass.
dot-products, and keeps in memory the Min and the Max dot products. In this scheme, each processor holds a different skewer which must be input before each new pass.
Algorithm 2: Parallel implementation of extreme projections step (rewritten to be split into  algorithm iterations).
algorithm iterations).
for ( ;
;  ;
;  ++)
++) //
// is the number of algorithm iterations
is the number of algorithm iterations
 ; //
; // denotes the number of skewers
denotes the number of skewers
for ( ;
;  ;
;  ++)
++) //
// denotes the number of pixels
denotes the number of pixels
par( ;
;  ;
;  ++)
++)
dp[ ]=dot_product(pixels[
]=dot_product(pixels[ ],skewers[
],skewers[ ]);
]);
if (dp[ ]
]  Min[
Min[ ])
])  Min[
Min[ ]=dp[
]=dp[ ]; Reg_Min[
]; Reg_Min[ ]=
]= ;
;
if (dp[ ]
]  Max[
Max[ ])
])  Max[
Max[ ]=dp[
]=dp[ ]; Reg_Max[
]; Reg_Max[ ]=
]= ;
;
 end par
end par
 end for
end for
 end for
end for
To conclude this section, we would like to emphasize the advantages of the considered parallelization strategy over other possible alternatives. For this purpose, Figure 5 compares the three parallelization strategies in Figure 4: parallelization by pixels (see Figure 4(b)), parallelization by skewers (see Figure 4(c)), and parallelization by skewers and pixels (see Figure 4(d)). The different parallel design strategies for the PPI algorithm have been described using VHDL language and we have used the Xilinx ISE environment to implement them and obtain the necessary resources (see Figure 5(a)) and the clock cycle (see Figure 5(b)) in each of the three parallelization strategies for the same number of dot-processing units. Once all the designs were implemented we measured their performance with clock-cycle accuracy. As shown in Figure 5, parallelization by skewers offers significant advantages with regards to the other considered implementation strategies.
4.2. Hardware Implementation
Figure 6 shows the architecture of the hardware used to implement the PPI algorithm, along with the I/O communications. For data input, we use a DDR2 SDRAM and a DMA (controlled by a PowerPC) with a Write FIFO to store pixel data. A Read FIFO and a transmitter are used to send the endmembers via an RS232 port. Finally, a systolic array and a random generation module are used to implement our version of the PPI algorithm.
Figure 7 describes the architecture of the dot-product processors used in our systolic array design. Basically, a systolic cycle consists of computing a single dot product between a pixel and a skewer to memorize the index of the pixel if the dot product is higher or smaller than a previously computed Max/Min value. Remember that a pixel is a vector of  spectral values, just like a skewer. A dot-product calculation between a pixel
spectral values, just like a skewer. A dot-product calculation between a pixel  and a
and a  can be simply obtained by using the expression
can be simply obtained by using the expression  . Therefore, a full vector dot-product calculation requires
. Therefore, a full vector dot-product calculation requires  multiplications and
multiplications and  additions, where
additions, where  is the number of spectral bands. As it was shown in previous work [25], the skewer values can be limited to a very small set of integers when
is the number of spectral bands. As it was shown in previous work [25], the skewer values can be limited to a very small set of integers when  is large, as in the case of hyperspectral images. A particular and interesting set is
is large, as in the case of hyperspectral images. A particular and interesting set is  since it avoids the multiplication. The dot product is, thus, reduced to an accumulation of positive and negative values. With the above assumptions in mind, each dot-product processor only needs to accumulate the positive or negative values of the pixel input according to the skewer input. These units are, thus, only composed of a single addition/subtraction operator and a register. The Min/Max unit receives the result of the dot product and compares it with the previous minimum and maximum values. If the result is a new minimum or maximum, it will be stored for future comparisons together with its corresponding index. For simplicity, the part related to the management of indexes has been omitted in Figure 7.
since it avoids the multiplication. The dot product is, thus, reduced to an accumulation of positive and negative values. With the above assumptions in mind, each dot-product processor only needs to accumulate the positive or negative values of the pixel input according to the skewer input. These units are, thus, only composed of a single addition/subtraction operator and a register. The Min/Max unit receives the result of the dot product and compares it with the previous minimum and maximum values. If the result is a new minimum or maximum, it will be stored for future comparisons together with its corresponding index. For simplicity, the part related to the management of indexes has been omitted in Figure 7.
Taking into account that the latency of an addition or a subtraction is just one clock cycle, then the calculation of a dot product requires  clock cycles. In each cycle, the processor sequentially receives the data of a pixel and accumulates the result, adding or subtracting, depending on the skewer component. The additional clock cycle is required for the comparison with a max and a min value and the pixel updating. We have evaluated different options to remove the last clock cycle, but finally we have decided to keep it. One option was to update the min and max indexes in parallel with the computation of the next dot product, but it requires a more complex hardware mechanism (at least two more registers) and makes this solution worse globally because we can synthesize less systolic processors on the FPGA. We can also update the pixel during the last clock cycle of each systolic cycle, but it increases the critical path and increases the clock frequency. Hence, when
clock cycles. In each cycle, the processor sequentially receives the data of a pixel and accumulates the result, adding or subtracting, depending on the skewer component. The additional clock cycle is required for the comparison with a max and a min value and the pixel updating. We have evaluated different options to remove the last clock cycle, but finally we have decided to keep it. One option was to update the min and max indexes in parallel with the computation of the next dot product, but it requires a more complex hardware mechanism (at least two more registers) and makes this solution worse globally because we can synthesize less systolic processors on the FPGA. We can also update the pixel during the last clock cycle of each systolic cycle, but it increases the critical path and increases the clock frequency. Hence, when  is a large number (as in the case of hyperspectral images), we obtain higher computation times.
is a large number (as in the case of hyperspectral images), we obtain higher computation times.
One of the main features of our system is the incorporation of a hardware-based random generation module that significantly reduces the I/O communications that, in previous implementations of the PPI, were the main bottleneck [20, 24, 25]. Previous works presented in [25, 27, 28] use the concept of the so-called block of skewers (BOSs) to generate the skewers. The idea of the BOS method is first to randomly generate  unit vectors, called independent skewer (Iskewers)
unit vectors, called independent skewer (Iskewers)  and then use them as a building blocks to generate the remaining skewers, called dependent skewers (Dskewers). The Dskewers are linear combination of the
and then use them as a building blocks to generate the remaining skewers, called dependent skewers (Dskewers). The Dskewers are linear combination of the  Iskewers. The goal of this approach is to reduce the number of dot products needed. The difference between the BOS method and the PPI is that the former uses the Dskewers to implement the PPI, while the skewers used in the latter are independently generated randomly. The work presented in [27] also analyses possible ways to further reduce the number of dot products and proposes to use FPGAs for the dot-products computations. In this work, we have implemented a random generator module similar to the one presented in [29]. This module provides pseudo-random and uniformly-distributed sequences using registers and XOR gates. Figure 8 shows the structure of the random generation module. It has two registers to store the new seeds. These seeds are initialized by the system each time that the PPI algorithm computes the image. At the beginning of every systolic cycle, we also store these two seeds in the other two registers. This generator reduces the number of resources needed because we do not need to store the
Iskewers. The goal of this approach is to reduce the number of dot products needed. The difference between the BOS method and the PPI is that the former uses the Dskewers to implement the PPI, while the skewers used in the latter are independently generated randomly. The work presented in [27] also analyses possible ways to further reduce the number of dot products and proposes to use FPGAs for the dot-products computations. In this work, we have implemented a random generator module similar to the one presented in [29]. This module provides pseudo-random and uniformly-distributed sequences using registers and XOR gates. Figure 8 shows the structure of the random generation module. It has two registers to store the new seeds. These seeds are initialized by the system each time that the PPI algorithm computes the image. At the beginning of every systolic cycle, we also store these two seeds in the other two registers. This generator reduces the number of resources needed because we do not need to store the  bits of
bits of  skewers, but only
skewers, but only  bits of two seeds. It requires an affordable amount of space (288 slices for 100 skewers) and it is able to generate the next component of every skewer in only one clock cycle and operates at a high clock frequency (664 MHz).
bits of two seeds. It requires an affordable amount of space (288 slices for 100 skewers) and it is able to generate the next component of every skewer in only one clock cycle and operates at a high clock frequency (664 MHz).
Our architecture can be seen as the pipeline shown in Figure 9. We can distinguish three stages which are communicated using FIFOs: The first stage provides the necessary data (seeds and image data) for the system, the second stage calculates the projections, and finally the endmembers are sent via a RS232 port by the third stage. Therefore, all stages are working in parallel.
To conclude this section, we provide a step-by-step description of how the proposed architecture performs the extraction of a set of endmembers from a hyperspectral image.
-
(i)
Firstly, to initialize the random generation module, the PowerPC generates two seeds of
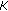 bits (where
bits (where 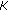 is the number of skewers) and writes them to the Write FIFO.
is the number of skewers) and writes them to the Write FIFO. -
(ii)
Afterwards, the control unit reads these seeds and sends them to the random generation module where they are stored. Hence, the random generation module can provide the systolic array with one bit for each skewer every clock cycle as we have described in this section.
-
(iii)
After the PowerPC has written the two seeds, it sends an order to the DMA to start copying a piece of the image from the DDR2 SDRAM to the Write FIFO. As mentioned before, the main bottleneck in this kind of system is frequently the data input which is addressed in our implementation by the incorporation of a DMA that eliminates most I/O overheads. Moreover, the PowerPC monitors the input FIFO and sends a new order to the DMA every time that it detects that the Write FIFO is half empty. This time, the DMA will bring a piece of the image that occupies half of the Write FIFO total capacity.
-
(iv)
When the data of the first pixel have been written in the Write FIFO, the systolic array and the random generation module start working. Every clock cycle, a new pixel is read by the control unit and sent to the systolic array. In parallel, the
 th component of each skewer also is sent to the systolic array by the random generation module.
th component of each skewer also is sent to the systolic array by the random generation module. -
(v)
During
 clock cycles, data of a pixel are accumulated positively or negatively depending of the skewer component. In the next clock cycle, the Min/Max unit updates the pixel and the random generation module restores the original two seeds, concluding the systolic cycle. In order to process the hyperspectral image, we need as many systolic cycles as pixels in the image. When the entire image is processed, the control unit writes the endmembers to the Read FIFO.
clock cycles, data of a pixel are accumulated positively or negatively depending of the skewer component. In the next clock cycle, the Min/Max unit updates the pixel and the random generation module restores the original two seeds, concluding the systolic cycle. In order to process the hyperspectral image, we need as many systolic cycles as pixels in the image. When the entire image is processed, the control unit writes the endmembers to the Read FIFO. -
(vi)
Finally, the Transmitter extracts the endmembers from the Read FIFO and sends them via an RS232 port.
-
(vii)
These steps are repeated several times depending on the number of skewers we can parallelize and the number of skewers we want to evaluate.
5. Experimental Results
5.1. FPGA Architecture
The hardware architecture described in Section 4 has been implemented using VHDL language for the specification of the systolic array. Further, we have used the Xilinx ISE environment and the Embedded Development Kit (EDK) environment (http://www.xilinx.com/ise/embedded/edk_pstudio.html) to specify the complete system. The full system has been implemented on an XUPV2P board, a low-cost reconfigurable board with a single Virtex-II PRO xc2vp30 FPGA component, a DDR SDRAM DIMM slot which holds up to 2 GBytes, an RS232 port, and some additional components not used by our implementation.
5.2. Hyperspectral Data
The hyperspectral dataset used in these experiments is the well-known AVIRIS Cuprite scene (see Figure 10(a)), available online in reflectance units (http://aviris.jpl.nasa.gov/html/aviris.freedata.html). This scene has been widely used to validate the performance of endmember extraction algorithms. The scene comprises a relatively large area (350 lines by 350 samples and 20-m pixels) and 224 spectral bands between 0.4 and 2.5  , with nominal spectral resolution of 10 nm. Bands 1–3, 105–115, and 150–170 were removed prior to the analysis due to water absorption and low SNR in those bands. The site is well understood mineralogically and has several exposed minerals of interest including alunite, buddingtonite, calcite, kaolinite, and muscovite. Reference ground signatures of the above minerals (see Figure 10(b)), available in the form of a US Geological Survey library (USGS) (http://speclab.cr.usgs.gov/spectral-lib.html), will be used to assess endmember signature purity in this work.
, with nominal spectral resolution of 10 nm. Bands 1–3, 105–115, and 150–170 were removed prior to the analysis due to water absorption and low SNR in those bands. The site is well understood mineralogically and has several exposed minerals of interest including alunite, buddingtonite, calcite, kaolinite, and muscovite. Reference ground signatures of the above minerals (see Figure 10(b)), available in the form of a US Geological Survey library (USGS) (http://speclab.cr.usgs.gov/spectral-lib.html), will be used to assess endmember signature purity in this work.
5.3. Endmember Extraction Accuracy Evaluation
Before analyzing the parallel properties of the proposed implementation, we first conducted an experiment-based cross-examination of endmember extraction accuracy to assess the spectral similarity between the USGS library spectra and the corresponding endmembers extracted by the considered implementation of the PPI algorithm. Table 1 shows the spectral angle distance (SAD) [3] between the most similar endmembers detected by the original ENVI implementation (using the supervised  -dimensional visualization tool to derive the final set of endmembers), the PPI approximation described in Section 3 (implemented in the C++ programming language), and our FPGA-based implementation. In all cases, we used
-dimensional visualization tool to derive the final set of endmembers), the PPI approximation described in Section 3 (implemented in the C++ programming language), and our FPGA-based implementation. In all cases, we used  skewers which provided the best compromise (after testing a wide range of values) and thus set the threshold value
skewers which provided the best compromise (after testing a wide range of values) and thus set the threshold value  to the mean of
to the mean of  scores obtained after
scores obtained after  iterations. It should be noted that the SAD between a pixel vector
iterations. It should be noted that the SAD between a pixel vector  selected by the PPI and a reference spectral signature
selected by the PPI and a reference spectral signature  is given by
is given by

In order to display the results in a more effective manner, we only report the SAD score associated to the most similar spectral endmember with regards to its corresponding USGS signature. It is important to emphasize that smaller SAD values indicate higher spectral similarity. As shown by Table 1, the two considered implementations did not produce exactly the same results as those obtained by the original PPI algorithm implemented in Research Systems ENVI 4.0. This is because ENVI's PPI implementation includes a manual supervision procedure to select the final endmembers and, hence, it is user dependent. In our experiments with the  -dimensional visualization tool available in ENVI, we made sure to perform many interactive rotations in order to select the best possible endmembers. In any event, both our PPI approximation in Section 3 and the FPGA implementation in Section 4 produced very similar results to those found by ENVI's PPI, but in a fully automatic fashion.
-dimensional visualization tool available in ENVI, we made sure to perform many interactive rotations in order to select the best possible endmembers. In any event, both our PPI approximation in Section 3 and the FPGA implementation in Section 4 produced very similar results to those found by ENVI's PPI, but in a fully automatic fashion.
5.4. Parallel Performance Evaluation
Table 2 shows the resources used for our hardware implementation of the proposed PPI algorithm design for different numbers of skewers (ranging from  to
to  ), tested on the Virtex-II PRO xc2vp30 FPGA of the XUPV2P board. This FPGA has a total of 13696 slices, 27392 slice flip flops, and 27392 four-input LUTs available. In addition, the FPGA includes some heterogeneous resources, such as two PowerPCs and distributed Block RAMs. In our implementation, we took advantage of these resources to optimize the design. One PowerPC monitors the communications and the Block RAMs are used to implement the FIFOs, so the vast majority of the slices are used for the implementation of the PPI algorithm. As shown by Table 2, we can scale our design up to 100 skewers (therefore,
), tested on the Virtex-II PRO xc2vp30 FPGA of the XUPV2P board. This FPGA has a total of 13696 slices, 27392 slice flip flops, and 27392 four-input LUTs available. In addition, the FPGA includes some heterogeneous resources, such as two PowerPCs and distributed Block RAMs. In our implementation, we took advantage of these resources to optimize the design. One PowerPC monitors the communications and the Block RAMs are used to implement the FIFOs, so the vast majority of the slices are used for the implementation of the PPI algorithm. As shown by Table 2, we can scale our design up to 100 skewers (therefore,  algorithm passes are needed in order to process
algorithm passes are needed in order to process  skewers). An interesting feature of our systolic array design is that we can scale it without increasing the delay of the critical path. Hence, the clock cycle remains constant at 187 MHz. Compared with the FPGA implementation of the FPPI algorithm presented in [20], our systolic array uses half of the slices and its clock frequency is 10 times higher. It should be noted that, in the current implementation, the complete AVIRIS hyperspectral image is stored in an external DDR2 SDRAM. Table 3 shows its characteristics. However, with an appropriate controller, other options could be supported, such as using flash memory to store the hyperspectral data.
skewers). An interesting feature of our systolic array design is that we can scale it without increasing the delay of the critical path. Hence, the clock cycle remains constant at 187 MHz. Compared with the FPGA implementation of the FPPI algorithm presented in [20], our systolic array uses half of the slices and its clock frequency is 10 times higher. It should be noted that, in the current implementation, the complete AVIRIS hyperspectral image is stored in an external DDR2 SDRAM. Table 3 shows its characteristics. However, with an appropriate controller, other options could be supported, such as using flash memory to store the hyperspectral data.
Frequently communications are the main bottleneck of a parallel system. Hence, we have paid special attention to this problem. In previous designs [10, 20], the random generation module was situated in an external processor. Hence, frequent communications were demanded. One of the improvements of our system is that we have developed a hardware random generation module based on the design proposed in [29]. This approach significantly reduces the I/O communications. Moreover, to further reduce the I/O overheads we have included DMA and we have applied a prefetching approach in order to hide the communication latency. Basically, while the systolic array is processing a set of data, the DMA is fetching the following set and storing it in the Write FIFO. Having in mind the proposed optimization concerning the use of available resources, it is important to find a balance between the number of DMA operations and the capacity of the destination FIFO. In other words, we need to fit enough information in the Write FIFO so that the systolic array never needs to stop. In addition, the greater the Write FIFO capacity, the fewer DMA operations will be required. We have evaluated several Write FIFO sizes and identified that, for 1024 positions or more, there are no penalties due to reading of the input data. To demonstrate the advantages of using a DMA, we have developed another version in which the image data are read from memory and written to the Write FIFO by the PowerPC instead of the DMA. In this version, the processing time was increased more than an order of magnitude (340 seconds) so we can conclude that the resources used for the DMA (621 slices) are well spent.
For illustrative purposes, we have performed a comparison of our proposed FPGA design with previous implementations in terms of computation time. As mentioned above, our FPGA-based implementation of the PPI algorithm can handle up to 100 skewers in parallel. Since  , the complete image has been processed
, the complete image has been processed  times. Table 4 shows the computing time for three different implementations: our PPI approximation in Section 3, an FPGA-based implementation presented in [20], and the FPGA-based implementation proposed in Section 4 of this paper. The PPI approximation was implemented in an AMD Athlon 2.6 GHz processor with 512 MB of RAM. The FPGA-based implementation in [20] was implemented in a Xilinx Virtex-II XC2V6000-6 FPGA with 33792 slices available. Finally, our proposed FPGA implementation was implemented on a Xilinx Virtex-II PRO xc2vp30 FPGA with 13696 slices available. As shown by Table 4, the FPGA-based implementation in [20] was more than 49 times faster than the PPI approximation for the AVIRIS Cuprite image, while our FPGA implementation of the PPI shows a significant increase in performance with regards to the FPGA-based implementation in [20], with a speedup of 2 with regard to that implementation. We must consider that the FPGA used in [20] has 2.5 times more slices than the one used in our implementation of the PPI algorithm. Furthermore, it is worth noting that we used a clock of 100 MHz (the maximum frequency available in EDK 9.1 for the Processor Local Bus [30]) for the calculation of the dot products. Therefore, we believe that there is still room for further improvements of the achieved computation time in future developments.
times. Table 4 shows the computing time for three different implementations: our PPI approximation in Section 3, an FPGA-based implementation presented in [20], and the FPGA-based implementation proposed in Section 4 of this paper. The PPI approximation was implemented in an AMD Athlon 2.6 GHz processor with 512 MB of RAM. The FPGA-based implementation in [20] was implemented in a Xilinx Virtex-II XC2V6000-6 FPGA with 33792 slices available. Finally, our proposed FPGA implementation was implemented on a Xilinx Virtex-II PRO xc2vp30 FPGA with 13696 slices available. As shown by Table 4, the FPGA-based implementation in [20] was more than 49 times faster than the PPI approximation for the AVIRIS Cuprite image, while our FPGA implementation of the PPI shows a significant increase in performance with regards to the FPGA-based implementation in [20], with a speedup of 2 with regard to that implementation. We must consider that the FPGA used in [20] has 2.5 times more slices than the one used in our implementation of the PPI algorithm. Furthermore, it is worth noting that we used a clock of 100 MHz (the maximum frequency available in EDK 9.1 for the Processor Local Bus [30]) for the calculation of the dot products. Therefore, we believe that there is still room for further improvements of the achieved computation time in future developments.
To conclude this section, we would like to show the execution time evolution as we increase the number of parallel dp units to calculate a fixed number of projections ( ). Figure 11 shows this evolution. We must consider that this behavior depends on the number of times we have to process the full image and therefore we are not always calculating
). Figure 11 shows this evolution. We must consider that this behavior depends on the number of times we have to process the full image and therefore we are not always calculating  projections. For example, if we have 90 dp units in parallel, we need almost 112 algorithm passes to calculate
projections. For example, if we have 90 dp units in parallel, we need almost 112 algorithm passes to calculate  projections or more, so we are really calculating
projections or more, so we are really calculating  projections.
projections.
6. Conclusions and Future Research Lines
On-board data processing of hyperspectral imagery has been a long-awaited goal by the remote sensing community. The number of applications requiring a response in real-time has been growing exponentially in recent years. Current sensor design practices could greatly benefit from the inclusion of specialized processing modules, such as FPGAs, which can be easily mounted or embedded in the sensor due to its compact size. In this paper, we have described an FPGA implementation of an advanced algorithm for information extraction from remotely sensed hyperspectral scenes. The algorithm selected for demonstration has been the Pixel Purity Index (PPI), one of the most well-known approaches for hyperspectral data analysis in the remote sensing community. Our experimental results, conducted on a Xilinx Virtex-II PRO xc2vp30 FPGA (a platform with the same architecture and similar area than radiation-hardened FPGAs that have been certified by international remote sensing agencies and are commonly used in airborne and spaceborne Earth Observation platforms), demonstrate that our hardware implementation makes appropriate use of computing resources in the considered architecture. Further, our proposed hardware version of the PPI algorithm can significantly outperform (in terms of computation time) the original (semisupervised) version of the algorithm, available in commercial software, a (fully automatic) approximation of the algorithm, and a recently developed FPGA implementation developed for a Xilinx Virtex-II XC2V6000-6 FPGA. Another interesting feature of our implementation is that it can be easily scaled to fit on larger FPGAs.
The reconfigurability of FPGA systems opens many innovative perspectives from the remote sensing application point of view, ranging from the appealing possibility of being able to adaptively select the data processing algorithm to be applied on board, out of a pool of available algorithms, from a control station on Earth immediately after the data is collected by the sensor, to the possibility of providing a real-time response in remote sensing applications with real-time requirements. As future work, we are investigating FPGA implementations of other endmember extraction algorithms based on different concepts and evaluating other specialized hardware platforms for on-board hyperspectral data exploitation, such as commodity graphics processing units (GPUs).
References
Goetz AFH, Vane G, Solomon JE, Rock BN: Imaging spectrometry for earth remote sensing. Science 1985, 228(4704):1147-1153. 10.1126/science.228.4704.1147
Green RO, Eastwood ML, Sarture CM, Chrien TG, Aronsson M, Chippendale BJ, Faust JA, Pavri BE, Chovit CJ, Solis M, Olah MR, Williams O: Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sensing of Environment 1998, 65(3):227-248. 10.1016/S0034-4257(98)00064-9
Chang C-I: Hyperspectral Imaging: Techniques for Spectral Detection and Classification. Kluwer, New York, NY, USA; 2003.
Adams JB, Smith MO, Johnson PE: Spectral mixture modeling: a new analysis of rock and soil types at the Viking Lander 1 site. Journal of Geophysical Research 1986, 91: 8098-8112. 10.1029/JB091iB08p08098
Plaza A, Martínez P, Pérez R, Plaza J: A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(3):650-663. 10.1109/TGRS.2003.820314
Plaza A, Chang C-I: High Performance Computing in Remote Sensing. CRC Press, Boca Raton, Fla, USA; 2007.
Boardman J: Automating spectral unmixing of AVIRIS data using convex geometry concepts. Summaries of Airborne Earth Science Workshop, 1993, JPL Publication 93–26 111-114.
Research Systems : ENVI User's Guide. Research Systems, Inc., Boulder, Colo, USA; 2001.
Plaza A, Chang C-I: Impact of initialization on design of endmember extraction algorithms. IEEE Transactions on Geoscience and Remote Sensing 2006, 44(11):3397-3407.
Chang C-I, Plaza A: A fast iterative algorithm for implementation of pixel purity index. IEEE Geoscience and Remote Sensing Letters 2006, 3(1):63-67. 10.1109/LGRS.2005.856701
Lysaght P, Blodget B, Mason J, Young J, Bridgford B: Enhanced architectures, design methodologies and CAD tools for dynamic reconfiguration of Xilinx FPGAS. Proceedings of the International Conference on Field Programmable Logic and Applications (FPL '06), August 2006 12-17.
Compton K, Hauck S: Reconfigurable computing: a survey of systems and software. ACM Computing Surveys 2002, 34(2):171-210. 10.1145/508352.508353
Tessier R, Burleson W: Reconfigurable computing for digital signal processing: a survey. Journal of VLSI Signal Processing Systems for Signal, Image, and Video Technology 2001, 28(1-2):7-27.
Buell D, El-Ghazawi T, Gaj K, Kindratenko V: Guest editors' introduction: high-performance reconfigurable computing. Computer 2007, 40(3):23-27.
El-Ghazawi T, El-Araby E, Huang M, Gaj K, Kindratenko V, Buell D: The promise of high-performance reconfigurable computing. Computer 2008, 41(2):69-76.
DeHon A, Wawrzynek J: Reconfigurable computing: what, why, and implications for design automation. Proceedings of the 36th Annual Design Automation Conference (DAC '99), June 1999 610-615.
Hauck S, DeHon A: Reconfigurable Computing: The Theory and Practice of FPGA-Based Computation. Morgan Kaufmann, San Francisco, Calif, USA; 2007.
Neil B, Dawood A: Reconfigurable computers in space: problems, solutions and future directions. Proceedings of the Military and Aerospace Applications of Programable Logic Devices Conference, 1999 http://klabs.org/richcontent/MAPLDCon99/Abstracts/bergmann.pdf
Fischman MA, Berkun AC, Cheng FT, Chun WW, Im E, Andraka R: Design and demostration of an advanced on-board processor for the second-generation precipitation radar. Proceedings of the IEEE Aerospace Conference, 2003 2: 1067-1075.
Valencia D, Plaza A, Vega-Rodríguez MA, Pérez RM: FPGA design and implementation of a fast pixel purity index algorithm for endmember extraction in hyperspectral imagery. Chemical and Biological Standoff Detection III, October 2005, Boston, Mass, USA, Proceedings of SPIE
El-Ghazawi T, Gaj K, Buell D, George A: Reconfigurable supercomputing. SuperComputing Tutorials, http://hpcl.seas.gwu.edu/docs/sc2005_part1.pdf
Thomson JT: Rad Hard FPGAs. http://esl.eng.ohio-state.edu/~rstheory/iip/RadHardFPGA.doc
Xilinx http://www.xilinx.com/publications/prod_mktg/AandDbrochure_2009.pdf
Lavenier D, Fabiani E, Derrien S, Wagner C: Systolic array for computing the pixel purity index (PPI) algorithm on hyper spectral images. Imaging Spectrometry VII, August 2002, San Diego, Calif, USA, Proceedings of SPIE 4480: 130-138.
Lavenier DD, Theiler JP, Szymanski JJ, Gokhale M, Frigo JR: FPGA implementation of the pixel purity index algorithm. Reconfigurable Technology: FPGAs for Computing and Applications II, November 2000, Boston, Mass, USA, Proceedings of SPIE 4212: 30-41.
Wildfore Reference Manual, revision 3.4 Annapolis Micro System Inc.; 1999.
Hsueh M, Chang C-I: Field programmable gate arrays (FPGA) for pixel purity index using blocks of skewers for endmember extraction in hyperspectral imagery. International Journal of High Performance Computing Applications 2008, 22(4):408-423. 10.1177/1094342007088378
Theiler J, Lavenier DD, Harvey NR, Perkins SJ, Szymanski JJ: Using blocks of skewers for faster computation of pixel purity index. Imaging Spectrometry VI, July 2000, San Diego, Calif, USA, Proceedings of SPIE 4132: 61-71.
Goretti M: Digital circuits based on FPGAs for random number generation. Department of Electricity and Electronics, University of Basque Country; 2006.
Xilinx http://www.xilinx.com/support/documentation/ip_documentation/plb_v34.pdf
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
González, C., Resano, J., Mozos, D. et al. FPGA Implementation of the Pixel Purity Index Algorithm for Remotely Sensed Hyperspectral Image Analysis. EURASIP J. Adv. Signal Process. 2010, 969806 (2010). https://doi.org/10.1155/2010/969806
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/969806

 in the input hyperspectral image cube
in the input hyperspectral image cube 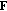 by generating
by generating  random,
random,  -dimensional vectors, called skewers.
-dimensional vectors, called skewers.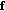 in the input data is projected onto the entire set of skewers
in the input data is projected onto the entire set of skewers  , and the pixels falling at the extremes of each skewer are tallied (see Figure
, and the pixels falling at the extremes of each skewer are tallied (see Figure  -dimensional visualizer, available as a built-in companion piece in ENVI software) and rotated until a desired number of endmembers are visually identified as extreme pixels in the data cloud.
-dimensional visualizer, available as a built-in companion piece in ENVI software) and rotated until a desired number of endmembers are visually identified as extreme pixels in the data cloud.

 .
. ,
, 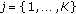 , all pixel vectors
, all pixel vectors 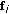 in the original data set F are projected onto
in the original data set F are projected onto  via dot products of
via dot products of  to find sample vectors at its extreme (maximum and minimum) projections, thus forming an extrema set for
to find sample vectors at its extreme (maximum and minimum) projections, thus forming an extrema set for 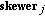 which is denoted by
which is denoted by 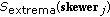 . Despite the fact that different skewers generate different extrema sets, it is very likely that some sample vectors may appear in more than one extrema set. To account for this, we define an indicator function of a set F, denoted by
. Despite the fact that different skewers generate different extrema sets, it is very likely that some sample vectors may appear in more than one extrema set. To account for this, we define an indicator function of a set F, denoted by  , to denote membership of an element x to that particular set as follows:
, to denote membership of an element x to that particular set as follows: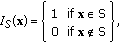
 (i.e., the number of times that a given pixel has been selected as extreme in step 2) using the following equation:
(i.e., the number of times that a given pixel has been selected as extreme in step 2) using the following equation:
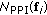 which are above
which are above  and label them as spectral endmembers. An optional postprocessing (not implemented in this work) based on removing potentially redundant endmembers may be also applied.
and label them as spectral endmembers. An optional postprocessing (not implemented in this work) based on removing potentially redundant endmembers may be also applied.





 bits (where
bits (where  is the number of skewers) and writes them to the Write FIFO.
is the number of skewers) and writes them to the Write FIFO. th component of each skewer also is sent to the systolic array by the random generation module.
th component of each skewer also is sent to the systolic array by the random generation module. clock cycles, data of a pixel are accumulated positively or negatively depending of the skewer component. In the next clock cycle, the Min/Max unit updates the pixel and the random generation module restores the original two seeds, concluding the systolic cycle. In order to process the hyperspectral image, we need as many systolic cycles as pixels in the image. When the entire image is processed, the control unit writes the endmembers to the Read FIFO.
clock cycles, data of a pixel are accumulated positively or negatively depending of the skewer component. In the next clock cycle, the Min/Max unit updates the pixel and the random generation module restores the original two seeds, concluding the systolic cycle. In order to process the hyperspectral image, we need as many systolic cycles as pixels in the image. When the entire image is processed, the control unit writes the endmembers to the Read FIFO.

 projections.
projections.