- Review
- Open access
- Published:
Overview of constrained PARAFAC models
EURASIP Journal on Advances in Signal Processing volume 2014, Article number: 142 (2014)
Abstract
In this paper, we present an overview of constrained parallel factor (PARAFAC) models where the constraints model linear dependencies among columns of the factor matrices of the tensor decomposition or, alternatively, the pattern of interactions between different modes of the tensor which are captured by the equivalent core tensor. Some tensor prerequisites with a particular emphasis on mode combination using Kronecker products of canonical vectors that makes easier matricization operations, are first introduced. This Kronecker product‐based approach is also formulated in terms of an index notation, which provides an original and concise formalism for both matricizing tensors and writing tensor models. Then, after a brief reminder of PARAFAC and Tucker models, two families of constrained tensor models, the co‐called PARALIND/CONFAC and PARATUCK models, are described in a unified framework, for N th‐order tensors. New tensor models, called nested Tucker models and block PARALIND/CONFAC models, are also introduced. A link between PARATUCK models and constrained PARAFAC models is then established. Finally, new uniqueness properties of PARATUCK models are deduced from sufficient conditions for essential uniqueness of their associated constrained PARAFAC models.
1 Review
1.1 Introduction
Tensor calculus was introduced in differential geometry, at the end of the nineteenth century, and then tensor analysis was developed in the context of Einstein’s theory of general relativity, with the introduction of index notation, the so‐called Einstein summation convention, at the beginning of the twentieth century, which allows to simplify and shorten physics equations involving tensors. Index notation is also useful for simplifying multivariate statistical calculations, particularly those involving cumulant tensors[1]. Generally speaking, tensors are used in physics and differential geometry for characterizing the properties of a physical system, representing fundamental laws of physics, and defining geometrical objects whose components are functions. When these functions are defined over a continuum of points of a mathematical space, the tensor forms what is called a tensor field, a generalization of vector field used to solve problems involving curved surfaces or spaces, as it is the case of curved space‐time in general relativity. From a mathematical point of view, two other approaches are possible for defining tensors, in terms of tensor products of vector spaces, or multilinear maps. Symmetric tensors can also be linked with homogeneous polynomials[2].
After the first tensor developments by mathematicians and physicists, the need of analyzing collections of data matrices that can be seen as three‐way data arrays gave rise to three‐way models for data analysis, with the pioneering works of Tucker in psychometrics[3], and Harshman in phonetics[4], who proposed what is now referred to as the Tucker and parallel factor (PARAFAC) decompositions, respectively. The PARAFAC decomposition was independently proposed by Carroll and Chang[5] under the name canonical decomposition (CANDECOMP) and then called CANDECOMP/PARAFAC (CP) in[6]. For a history of the development of multi‐way models in the context of data analysis, see[7]. Since the 1990s, multi‐way analysis has known a growing success in chemistry and especially in chemometrics (see Bro’s thesis[8] and the book by Smilde et al.[9] for a description of various chemical applications of three‐way models, with a pedagogical presentation of these models and of various algorithms for estimating their parameters). At the same period, tensor tools were developed for signal processing applications, more particularly for solving the so‐called blind source separation (BSS) problem using cumulant tensors (see[10]‐[12] and De Lathauwer’s thesis[13] where the concept of high‐order singular value decomposition (HOSVD) is introduced, a tensor tool generalizing the standard matrix SVD to arrays of order higher than two). A recent overview of BSS approaches and applications can be found in the handbook co‐edited by Comon and Jutten[14].
Nowadays, (high‐order) tensors, also called multi‐way arrays in the data analysis community, play an important role in many fields of application for representing and analyzing multidimensional data, as in psychometrics, chemometrics, food industry, environmental sciences, signal/image processing, computer vision, neuroscience, information sciences, data mining, pattern recognition, among many others. Then, they are simply considered as multidimensional arrays of numbers, constituting a generalization of vectors and matrices that are first‐ and second‐order tensors, respectively, to orders higher than two. Tensor decompositions, also called tensor models, are very useful for analyzing multidimensional data under the form of signals, images, speech, music sequences, or texts and also for designing new systems as it is the case of wireless communication systems since the publication of the seminal paper by Sidiropoulos et al.[15]. Besides the references already cited, overviews of tensor tools, models, algorithms, and applications can be found in[16]‐[19].
Tensor models incorporating constraints (sparsity; non‐negativity; smoothness; symmetry; column orthonormality of factor matrices; Hankel, Toeplitz, and Vandermonde structured matrix factors; allocation constraints...) have been the object of intensive works, during the last years. Such constraints can be inherent to the problem under study or the result of a system design. An overview of constraints on components of tensor models most often encountered in multi‐way data analysis can be found in[7]. Incorporation of constraints in tensor models may facilitate physical interpretability of matrix factors. Moreover, imposing constraints may allow to relax uniqueness conditions and to develop specialized parameter estimation algorithms with improved performance both in terms of accuracy and computational cost, as it is the case of CP models with a column‐wise orthonormal factor matrix[20]. One can classify the constraints into three main categories: i) sparsity/non‐negativity, ii) structural, and iii) linear dependencies/mode interactions. It is worth noting that the three categories of constraints involve specific parameter estimation algorithms, the first two generally inducing an improvement of uniqueness property of the tensor decomposition, while the third category implies a reduction of uniqueness, named partial uniqueness. We briefly review the main results concerning the first two types of constraints, Section 1.3 of this paper being dedicated to the third category.
Sparse and non‐negative tensor models have recently been the subject of many works in various fields of applications like computer vision[21, 22], image compression[23], hyperspectral imaging[24], music genre classification[25] and audio source separation[26], multi‐channel EEG (electroencephalography) and network traffic analysis[27], fluorescence analysis[28], data denoising and image classification[29], among many others. Two non‐negative tensor models have been more particularly studied in the literature, the so‐called non‐negative tensor factorization (NTF), i.e., PARAFAC models with non‐negativity constraints on the matrix factors, and non‐negative Tucker decomposition (NTD), i.e., Tucker models with non‐negativity constraints on the core tensor and/or the matrix factors. The crucial importance of NTF/NTD for multi‐way data analysis applications results from the very large volume of real‐world data to be analyzed under constraints of sparseness and non‐negativity of factors to be estimated, when only non‐negative parameters are physically interpretable. Many NTF/NTD algorithms are now available. Most of them can be viewed as high‐order extensions of non‐negative matrix factorization (NMF) methods, in the sense that they are based on an alternating minimization of cost functions incorporating sparsity measures (also named distances or divergences) with application of NMF methods to matricized or vectorized forms of the tensor to be decomposed (see for instance[16, 23, 28, 30] for NTF and[29, 31] for NTD). An overview of NMF and NTF/NTD algorithms can be found in[16].
The second category of constraints concerns the case where the core tensor and/or some matrix factors of the tensor model have a special structure. For instance, we recently proposed a nonlinear CDMA scheme for multiuser SIMO communication systems that is based on a constrained block‐Tucker2 model whose core tensor, composed of the information symbols to be transmitted and their powers up to a certain degree, is characterized by matrix slices having a Vandermonde or a Hankel structure[32, 33]. We also developed Volterra‐PARAFAC models for nonlinear system modeling and identification. These models are obtained by expanding high‐order Volterra kernels, viewed as symmetric tensors, by means of symmetric or doubly symmetric PARAFAC decompositions[34, 35]. Block structured nonlinear systems like Wiener, Hammerstein, and parallel‐cascade Wiener systems can be identified from their associated Volterra kernels that admit symmetric PARAFAC decompositions with Toeplitz factors[36, 37]. Symmetric PARAFAC models with Hankel factors and symmetric block PARAFAC models with block Hankel factors are encountered for blind identification of multiple‐input multiple‐output (MIMO) linear channels using fourth‐order cumulant tensors, in the cases of memoryless and convolutive channels, respectively[38, 39]. In the presence of structural constraints, specific estimation algorithms can be derived as it is the case for symmetric CP decompositions[40], CP decompositions with Toeplitz factors (in[41], an iterative solution was proposed, whereas in[42], a non‐iterative algorithm was developed), Vandermonde factors[43], circulant factors[44], banded and/or structured matrix factors[45, 46], and also for Hankel and Vandermonde structured core tensors[33].
The rest of this paper is organized as follows: In Section 1.2, we present some tensor prerequisites with a particular emphasis on mode combination using Kronecker products of canonical vectors that makes easier the matricization operations, especially to derive matrix representations of tensor models. This Kronecker product‐based approach is also formulated in terms of an index notation, which provides an original and concise formalism for both matricizing tensors and writing tensor models. Then, we present the two most common tensor models, the so‐called Tucker and PARAFAC models, in a general framework, i.e., for N th‐order tensors. In Section 1.3, two families of constrained tensor models, the co‐called PARALIND/CONFAC and PARATUCK models, are described in a unified way, with a generalization to N th‐order tensors. New tensor models, called nested Tucker models and block PARALIND/CONFAC models, are also introduced. A link between PARATUCK models and constrained PARAFAC models is also established. In Section 1.4, uniqueness properties of PARATUCK models are deduced using this link. The paper is concluded in Section 2.
Notations and definitions. and
and denote the fields of real and complex numbers, respectively. Scalars, column vectors, matrices, and high‐order tensors are denoted by lowercase, boldface lowercase, boldface uppercase, and calligraphic uppercase letters, e.g., a, a, A, and
denote the fields of real and complex numbers, respectively. Scalars, column vectors, matrices, and high‐order tensors are denoted by lowercase, boldface lowercase, boldface uppercase, and calligraphic uppercase letters, e.g., a, a, A, and , respectively. The vector Ai. (resp. A.j) represents the i th row (resp. j th column) of A.
, respectively. The vector Ai. (resp. A.j) represents the i th row (resp. j th column) of A.
I N ,, and stand for the identity matrix of order N, the all‐ones row vector of dimensions 1×N, and the n th canonical vector of the Euclidean space, respectively.
AT, AH, A†, tr (A), and r
A
denote the transpose, the conjugate (Hermitian) transpose, the Moore‐Penrose pseudo‐inverse, the trace, and the rank of A, respectively. D
i
(A)=diag(Ai.) represents the diagonal matrix having the elements of the i th row of A on its diagonal. The operator bdiag(.) forms a block diagonal matrix from its matrix arguments, while the operator vec(.) transforms a matrix into a column vector by stacking the columns of its matrix argument one on top of the other one. In case of a tensor , the vec(.) operation is defined in (6).
, the vec(.) operation is defined in (6).
The outer product (also called tensor product), and the matrix Kronecker, Khatri‐Rao (column‐wise Kronecker), and Hadamard (element‐wise) products are denoted by ∘, ⊗, ◇, and ⊙, respectively.
Let us consider the set obtained by permuting the elements of the set {1,…,N}. For and, n=1,…,N, we define
The outer product of N non‐zero vectors defines a rank‐one tensor of order N.
By convention, the order of dimensions is directly related to the order of variation of the associated indices. For instance, in (1) and (2), the product of dimensions means that n1 is the index varying the most slowly while n N is the index varying the most fastly in the Kronecker products computation.
For, we have the following identities:
In particular, for
Some useful matrix formulae are recalled in Appendix 1.
1.2 Tensor prerequisites
In this paper, a tensor is simply viewed as a multidimensional array of measurements. Depending that these measurements are real‐ or complex‐valued, we have a real‐ or complex‐valued tensor, respectively. The order N of a tensor refers to the number of indices that characterize its elements, each index i n (i n =1,…,I N ,for n=1,…,N) being associated with a dimension, also called a way, or a mode, and I n denoting the mode‐n dimension.
An N th‐order complex‐valued tensor, also called an N‐way array, of dimensions I1×⋯×I N , can be written as
The coefficients represent the coordinates of in the canonical basis of the space.
in the canonical basis of the space.
The identity tensor of order N and dimensions I×⋯×I, denoted by or simply , is a diagonal hypercubic tensor whose elements are defined by means of the generalized Kronecker delta, i.e.,, and I
n
=I,∀n=1,…,N. It can be written as
, is a diagonal hypercubic tensor whose elements are defined by means of the generalized Kronecker delta, i.e.,, and I
n
=I,∀n=1,…,N. It can be written as
Different reduced order tensors can be obtained by slicing the tensor along one mode or p modes, i.e., by fixing one index i
n
or a set of p indices, which gives a tensor of order N-1 or N-p, respectively. For instance, by slicing along its mode‐n, we get the mode‐n slice of
along its mode‐n, we get the mode‐n slice of , denoted by, that can be written as
, denoted by, that can be written as
For instance, by slicing the third‐order tensor along each mode, we get three types of matrix slices, respectively called horizontal, lateral, and frontal slices:
1.2.1 Tensor Hadamard product
Consider and, where and are two disjoint ordered subsets of the set of indices {i1,…,i P } and.
We define the Hadamard product of with
with along their common modes, as the tensor such that
along their common modes, as the tensor such that
For instance, given two third‐order tensors and, the Hadamard product gives a fourth‐order tensor such that
Such a tensor Hadamard product can be calculated by means of the matrix Hadamard product of matrix unfoldings of extended tensors, as defined in (21) and (22) (see also (94) to (96) in Appendix 2). For the example above, we have
1.2.1.0 Example
For,, and the tensor such as, a mode‐1 flat matrix unfolding of
such as, a mode‐1 flat matrix unfolding of is given by
is given by
1.2.2 Mode combination
Different contraction operations can be defined depending on the way according to which the modes are combined. Let us partition the set {1,…,N} in N1 ordered subsets, constituted of p(n1) elements with. Each subset is associated with a combined mode of dimension. These mode combinations allow to rewrite the N th‐order tensor under the form of an‐order tensor as follows
Two particular mode combinations corresponding to the vectorization and matricization operations are now detailed.
1.2.3 Vectorization
The vectorization of is associated with a combination of the N modes into a unique mode of dimension, which amounts to replace the outer product in (4) by the Kronecker product
the element of being the i th entry of with i defined as in (3).
being the i th entry of with i defined as in (3).
The vectorization can also be carried out after a permutation of indices π(i n ),n=1,…,N.
1.2.4 Matricization or unfolding
There are different ways of matricizing the tensor according to the partitioning of the set {1,…,N} into two ordered subsets and, constituted of p and N-p indices, respectively. A general formula for the matricization, for, is
according to the partitioning of the set {1,…,N} into two ordered subsets and, constituted of p and N-p indices, respectively. A general formula for the matricization, for, is
with, for n1=1 and 2. From (7), we can deduce the following expression of the element in terms of the matrix unfolding
1.2.5 Particular case: mode‐ n matrix unfoldings X n
A flat mode‐n matrix unfolding of the tensor corresponds to an unfolding under the form with and, which gives
corresponds to an unfolding under the form with and, which gives
We can also define a tall mode‐n matrix unfolding of , by choosing and. Then, we have.
, by choosing and. Then, we have.
The column vectors of a flat mode‐n matrix unfolding X
n
are the mode‐n vectors of , and the rank of X
n
, i.e., the dimension of the mode‐n linear space spanned by the mode‐n vectors, is called mode‐n rank of
, and the rank of X
n
, i.e., the dimension of the mode‐n linear space spanned by the mode‐n vectors, is called mode‐n rank of , denoted by.
, denoted by.
In the case of a third‐order tensor, there are six different flat unfoldings, denoted XI×J K, XI×K J, XJ×K I, XJ×I K, XK×I J, and XK×J I. For instance, we have
Using the properties (84), (85), and (87) of the Kronecker product gives
Similarly, there are six tall matrix unfoldings, denoted XJ K×I, XK J×I, XK I×J, XI K×J, XI J×K, XJ I×K, like for instance
Applying (8) to (10) gives
1.2.6 Mode‐ n product of a tensor with a matrix or a vector
The mode‐n product of with along the n th mode, denoted by, gives the tensor of order N and dimensions I1×⋯×In-1×J
n
×In+1×⋯×I
N
, such as[47]
of order N and dimensions I1×⋯×In-1×J
n
×In+1×⋯×I
N
, such as[47]
which can be expressed in terms of mode‐n matrix unfoldings of and
and
This operation can be interpreted as the linear map from the mode‐n space of to the mode‐n space of
to the mode‐n space of , associated with the matrix A.
, associated with the matrix A.
The mode‐n product of with the row vector along the n th mode, denoted by, gives a tensor of order N-1 and dimensions I1×⋯×In-1×In+1×⋯×I
N
, such as
of order N-1 and dimensions I1×⋯×In-1×In+1×⋯×I
N
, such as
that can be written in vectorized form as.
When multiplying a N th‐order tensor by row vectors along p different modes, we get a tensor of order N-p. For instance, for a third‐order tensor, we have
Considering an ordered subset of the set {1,…,N}, a series of mode‐ m p products of with, p∈{1,…,P}, P≤N, will be concisely noted as
1.2.6.0 Properties
-
For any permutation π(.) of P distinct indices m p ∈{1,…,N} such as q p =π(m p ), p∈{1,…,P}, with P≤N, we have
which means that the order of the mode‐ m p products is irrelevant when the indices m p are all distinct.
-
For two products of along the same mode‐n, with and, we have[13]
(13)
1.2.7 Kronecker product‐based approach using index notation
In this subsection, we propose to reformulate our Kronecker product‐based approach for tensor matricization in terms of an index notation introduced in[48]. Using this index notation, for,, and, we can write
As with Einstein summation convention, the index notation allows to drop summation signs. If an index i∈[ 1,I] is repeated in an expression (or more generally in a term of an equation), it means that this expression (or this term) must be summed over that index from 1 to I. However, it is worth noting the two differences between the index notation used in this paper and Einstein summation convention: (i) each index can be repeated more than twice in any expression and (i i) the index notation can be used with ordered sets of indices. We have to notice that the index notation can be interpreted in terms of two separate combinations of indices, one associated with the column (superscript) indices and the other one with the row (subscript) indices, with the following rules:
-
the ordering of the column indices is independent of that of the row indices;
-
the ordering of the column and row indices cannot be changed.
Considering the set obtained by permuting the elements of {1,…,N} and defining the ordered set of indices associated with , we denote by and the Kronecker products and, respectively. So, we have
, we denote by and the Kronecker products and, respectively. So, we have
Partitioning two ordered sets of indices and
and into two subsets () and (), respectively, the rules enounced previously imply the following identities:
into two subsets () and (), respectively, the rules enounced previously imply the following identities:
These identities directly result from the property that the Kronecker product of a column vector with a row vector is independent of the order of the vectors (u⊗vT=vT⊗u), which implies that in a sequence of Kronecker products of column and row vectors, a column vector can be permuted with a row vector without altering the final result, if the proper ordering of the column vectors and of the row vectors is not changed in the sequence ( if u1≠u2).
Using the index notation, the horizontal, lateral, and frontal slices of a third‐order tensor can be written as
The Kronecker products of vectors () and matrices () can be concisely written as
For and, we have
where the summation over n is to be done after the matricization u(n)(v(n))T.
Using the index notation, the Khatri‐Rao product can be written as follows:
The Kronecker and Khatri‐Rao products defined in (1) and (2), with as entry of A(n), can then be defined as
where.
Applying these results, the unfoldings (7), (10), and (11) and the formula (8) can be rewritten respectively as
where and represent the sets of indices i n associated with the sets and of index n, respectively.
We can also use the index notation for deriving matrix unfoldings of tensor extensions of a matrix. For instance, if we define the tensor such as ai,j,k=bi,j for k=1,…,K, mode‐1 flat unfoldings of are given by
are given by
These two formulae will be used later for establishing the link between PARATUCK‐(2,4) models and constrained PARAFAC‐4 models.
1.2.8 Basic tensor models
We now present the two most common tensor models, i.e., the Tucker[3] and PARAFAC[4] models. In[7], these models are introduced in a constructive way, in the context of a three‐way data analysis. The Tucker models are presented as extensions of the matrix singular value decomposition (SVD) to three‐way arrays, which gave rise to the generalization as HOSVD[13, 49], whereas the PARAFAC model is introduced by emphasizing Cattell’s principle of parallel proportional profiles[50] that underlies this model, so explaining the acronym PARAFAC. In the following, we adopt a more general presentation for multi‐way arrays, i.e., tensors of any order N.
1.2.8.0 Tucker models
For a N th‐order tensor, a Tucker model is defined in an element‐wise form as
with i n =1,…,I n for n=1,…,N, where is an element of the core tensor and is an element of the matrix factor.
Using the index notation and defining the set of indices, the Tucker model can also be written simply as
Taking the definition (4) into account and noting that, this model can be written as a weighted sum of outer products, i.e., rank‐one tensors
Using the definition (12) allows to write (23) in terms of mode‐n products as
This expression evidences that the Tucker model can be viewed as the transformation of the core tensor resulting from its multiplication by the factor matrix A(n) along its mode‐n, which corresponds to a linear map applied to the mode‐n space of , for n=1,…,N, i.e., a multilinear map applied to
, for n=1,…,N, i.e., a multilinear map applied to . From a transformation point of view,
. From a transformation point of view, and
and can be interpreted as the input tensor and the transformed tensor, or output tensor, respectively.
can be interpreted as the input tensor and the transformed tensor, or output tensor, respectively.
Matrix representations of the Tucker model. A matrix representation of a Tucker model is directly linked with a matricization of tensor like (7), corresponding to the combination of two sets of modes and. These combinations must be applied both to the tensor and its core tensor
and its core tensor .
.
The matrix representation (7) of the Tucker model (23) is given by
with, and, for n1=1 and 2.
Proof
See Appendix 3.
For the flat mode‐n unfolding, defined in (9), the formula (27) gives
Applying the vec formula (92) to the right‐hand side of (28), we obtain the vectorized form of associated with its mode‐n unfolding X
n
associated with its mode‐n unfolding X
n
1.2.8.0 Tucker‐(N 1 ,N) models
A Tucker‐ (N1,N) model for a N th‐order tensor, with N≥N1, corresponds to the case where N-N1 factor matrices are equal to identity matrices. For instance, assuming that, which implies R n =I n , for n=N1+1,…,N, (23) and (26) become
One such model that is currently used in applications is the Tucker‐(2,3) model, usually denoted Tucker2, for third‐order tensors. Assuming, and, such a model is defined by the following equations:
with the core tensor.
1.2.8.0 PARAFAC models
A PARAFAC model for a N th‐order tensor corresponds to the particular case of a Tucker model with an identity core tensor of order N and dimensions R×⋯×R
(23) to (26) then become, respectively
with the factor matrices.
1.2.8.0 Remarks
-
The expression (33) as a sum of polyads is called a polyadic form of
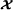 by Hitchcock[51].
by Hitchcock[51]. -
The PARAFAC model (33, 34 and 35) amounts to decomposing the tensor
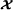 into a sum of R components, each component being a rank‐one tensor. When R is minimal in (33), it is called the rank of
into a sum of R components, each component being a rank‐one tensor. When R is minimal in (33), it is called the rank of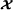 [52]. This rank is related to the mode‐n ranks by the following inequalities. Furthermore, contrary to the matrices for which the rank is always at most equal to the smallest of the dimensions, for higher‐order tensors, the rank can exceed any mode‐n dimension I
n
.
[52]. This rank is related to the mode‐n ranks by the following inequalities. Furthermore, contrary to the matrices for which the rank is always at most equal to the smallest of the dimensions, for higher‐order tensors, the rank can exceed any mode‐n dimension I
n
. -
There exists different definitions of rank for tensors, like typical and generic ranks, or also symmetric rank for a symmetric tensor (see[53, 54] for more details).
-
In telecommunication applications, the structure parameters (rank, mode dimensions, and core tensor dimensions) of a PARAFAC or Tucker model are design parameters that are chosen in function of the performance desired for the communication system. However, in most of the applications, as for instance in multi‐way data analysis, the structure parameters are generally unknown and must be determined a priori. Several techniques have been proposed for determining these parameters (see[55]‐[58] and references therein).
-
The PARAFAC model is also sometimes defined by the following equation
(36) -
In this case, the identity tensor in (35) is replaced by the diagonal tensor whose diagonal elements are equal to scaling factors g r , i.e.
and all the column vectors are normalized, i.e., with a unit norm, for 1≤n≤N.
-
It is important to notice that the PARAFAC model (33) is multilinear (more precisely N‐linear) in its parameters in the sense that it is linear with respect to each matrix factor. This multilinearity property is exploited for parameter estimation using the standard alternating least squares (ALS) algorithm[4, 5] that consists in alternately estimating each matrix factor by minimizing a least squares error criterion conditionally to the knowledge of the other matrix factors that are fixed with their previously estimated values.
Matrix representations of the PARAFAC model. The matrix representation (7) of the PARAFAC model (33)‐(35) is given by
Proof.
See Appendix 4.
1.2.8.0 Remarks
-
From (37), we can deduce that a mode combination results in a Khatri‐Rao product of the corresponding factor matrices. Consequently, the tensor contraction (5) associated with the PARAFAC‐N model (35) gives a PARAFAC‐ N1 model whose factor matrices are equal to, n1=1,…,N1, with.
-
For the PARAFAC model, the flat mode‐n unfolding, defined in (9), is given by
(38) -
and the associated vectorized form is obtained in applying the vec formula (93) to the right‐hand side of the above equation, with I R =diag(1 R )
(39) -
In the case of the normalized PARAFAC model (36), (37) and (39) become, respectively,
-
where.
-
For the PARAFAC model of a third‐order tensor with factor matrices (A,B,C), the formula (37) gives for and
-
Noting that, we deduce the following expression for mode‐1 matrix slices
-
Similarly, we have
-
For the PARAFAC model of a fourth‐order tensor with factor matrices (A,B,C,D), we obtain
(40)Other matrix slices can be deduced from (40) by simple permutations of the matrix factors.
In the next section, we introduce two constrained PARAFAC models, the so‐called PARALIND and CONFAC models, and then PARATUCK models.
1.3 Constrained PARAFAC models
The introduction of constraints in tensor models can result from the system itself that is under study or from a system design. In the first case, the constraints are often interpreted as interactions or linear dependencies between the PARAFAC factors. Examples of such dependencies are encountered in psychometric and chemometric applications that gave origin, respectively, to the PARATUCK‐2 model[59] and the parallel profiles with linear dependencies (PARALIND) model[60, 61], introduced in[47] under the name canonical decomposition with linear constraints (CANDELINC), for the multiway case. A first application of the PARATUCK‐2 model in signal processing was made in[62] for blind joint identification and equalization of Wiener‐Hammerstein communication channels. The PARALIND model was applied for identifiability and propagation parameter estimation purposes in a context of array signal processing[63, 64].
In the second case, the constraints are used as design parameters. For instance, in a telecommunications context, we proposed two constrained tensor models: the CONFAC (constrained factor) model[65] and the PARATUCK‐ (N1,N) model[66, 67]. The PARATUCK‐2 model was also applied for designing space‐time spreading‐multiplexing MIMO systems[68]. For these telecommunication applications of constrained tensor models, the constraints are used for resource allocation. We are now going to describe these various constrained PARAFAC models.
1.3.1 PARALIND models
Let us define the core tensor of the Tucker model (26) as follows:
where, with, are constraint matrices. In this case, will be called the ‘interaction tensor’, or ‘constraint tensor’.
will be called the ‘interaction tensor’, or ‘constraint tensor’.
The PARALIND model is obtained by substituting (41) into (26) and applying the property (13), which gives
This equation leads to two different interpretations of the PARALIND model, as a constrained Tucker model whose core tensor admits a PARAFAC decomposition with factor matrices Φ(n), called ‘interaction matrices,’ and as a constrained PARAFAC model with constrained factor matrices.
The interaction matrix Φ(n) allows taking into account linear dependencies between the columns of A(n), implying a rank deficiency for this factor matrix. When the columns of Φ(n) are formed with 0’s and 1’s, the dependencies simply consist in a repetition or an addition of certain columns of A(n). In this particular case, the diagonal element of the matrix represents the number of columns of A(n) that are added to form the r th column of the constrained factor A(n)Φ(n). The choice means that there is no such dependency among the columns of A(n).
Note that (42) can be written element‐wise as
This constrained PARAFAC model constitutes an N‐way form of the three‐way PARALIND model, used for chemometric applications in[60, 61].
1.3.2 CONFAC models
When the constraint matrices are full row rank and their columns are chosen as canonical vectors of the Euclidean space, for n=1,…,N, the constrained PARAFAC model (42) constitutes a generalization to N th‐order of the third‐order CONFAC model, introduced in[65] for designing MIMO communication systems with resource allocation. This CONFAC model was used in[69] for solving the problem of blind identification of underdetermined mixtures based on cumulant generating function of the observations. In a telecommunications context where represents the tensor of received signals, such a constraint matrix Φ(n) can be interpreted as an ‘allocation matrix’ allowing to allocate resources, like data streams, codes, and transmit antennas, to the R components of the signal to be transmitted. In this case, the core tensor
represents the tensor of received signals, such a constraint matrix Φ(n) can be interpreted as an ‘allocation matrix’ allowing to allocate resources, like data streams, codes, and transmit antennas, to the R components of the signal to be transmitted. In this case, the core tensor will be called the ‘allocation tensor.’ By assumption, each column of the allocation matrix Φ(n) is a canonical vector of, which means that there is only one value of r
n
such that, and this value of r
n
corresponds to the n th resource allocated to the r th component.
will be called the ‘allocation tensor.’ By assumption, each column of the allocation matrix Φ(n) is a canonical vector of, which means that there is only one value of r
n
such that, and this value of r
n
corresponds to the n th resource allocated to the r th component.
Each element of the received signal tensor is equal to the sum of R components, each component r resulting from the combination of N resources, each resource being associated with a column of the matrix factor A(n), n=1,…,N. This combination, determined by the allocation matrices, is defined by a set of N indices {r1,…,r
N
} such that. As for any, there is one and only one N‐uplet (r1,…,r
N
) such as, we can deduce that each component r of in (43) is the result of one and only one combination of the N resources under the form of the product. For the CONFAC model, we have
is equal to the sum of R components, each component r resulting from the combination of N resources, each resource being associated with a column of the matrix factor A(n), n=1,…,N. This combination, determined by the allocation matrices, is defined by a set of N indices {r1,…,r
N
} such that. As for any, there is one and only one N‐uplet (r1,…,r
N
) such as, we can deduce that each component r of in (43) is the result of one and only one combination of the N resources under the form of the product. For the CONFAC model, we have
meaning that each resource r n is allocated at least once, and the diagonal element of Ξ(n)=Φ(n)TΦ(n) is such as, because only one resource r n is allocated to each component r. Moreover, we have to notice that the assumption implies that each resource can be allocated several times, i.e., to several components. Defining the interaction matrices
the diagonal element represents the number of times that the column of A(n) is repeated, i.e., the number of times that the resource is allocated to the R components, whereas determines the number of interactions between the column of and the column of, i.e., the number of times that the and resources are combined in the R components. If we choose R n =R and, the PARALIND/CONFAC model (42) becomes identical to the PARAFAC one (35).
The matrix representation (7) of the PARALIND/CONFAC model can be deduced from (37) in replacing A(n) by A(n)Φ(n)
Using the identity, (86) gives
or, equivalently,
where the matrix representation of the constraint/allocation tensor , defined by means of its PARAFAC model (41), can also be deduced from (37) as
, defined by means of its PARAFAC model (41), can also be deduced from (37) as
1.3.3 Nested Tucker models
The PARALIND/CONFAC models can be viewed as particular cases of a new family of tensor models that we shall call nested Tucker models, defined by means of the following recursive equation:
with the factor matrices for p=1,…,P, such as R(0,n)=R
n
and R(P,n)=I
n
, for n=1,…,N, the core tensor, and. This equation can be interpreted as P successive linear transformations applied to each mode‐n space of the core tensor . So, P nested Tucker models can then be interpreted as a Tucker model for which the factor matrices are products of P matrices. When, which implies R(0,n)=R
n
=R for n=1,…,N, we obtain nested PARAFAC models. The PARALIND/CONFAC models correspond to two nested PARAFAC models (P=2), with A(1,n)=Φ(n), A(2,n)=A(n), R(0,n)=R, R(1,n)=R
n
, and R(2,n)=I
n
, for n=1,…,N.
. So, P nested Tucker models can then be interpreted as a Tucker model for which the factor matrices are products of P matrices. When, which implies R(0,n)=R
n
=R for n=1,…,N, we obtain nested PARAFAC models. The PARALIND/CONFAC models correspond to two nested PARAFAC models (P=2), with A(1,n)=Φ(n), A(2,n)=A(n), R(0,n)=R, R(1,n)=R
n
, and R(2,n)=I
n
, for n=1,…,N.
By considering nested PARAFAC models with P=3,,, and, for n=1,…,N, we deduce doubly PARALIND/CONFAC models described by the following equation:
Such a model can be viewed as a doubly constrained PARAFAC model, with factor matrices Ψ(n)A(n)Φ(n), the constraint matrix Ψ(n), assumed to be full column rank, allowing to take into account linear dependencies between the rows of A(n). A third‐order nested Tucker model is visualized in Figure1.
1.3.4 Block PARALIND/CONFAC models
In some applications, the data tensor is written as a sum of P sub‐tensors, each sub‐tensor admitting a tensor model with a possibly different structure. So, we can define a block‐PARALIND/CONFAC model as
where,, and are the mode‐n factor matrix, the mode‐n constraint/allocation matrix, and the core tensor of the PARALIND/CONFAC model of the p th sub‐tensor, respectively. The matrix representation (44) then becomes
Defining the following block partitioned matrices
where, (47) can be rewritten in the following more compact form
where ⊗ b denotes the block‐wise Kronecker product defined as
A(q) being partitioned in P blocks as in (48), and
where ◇ b denotes the block‐wise Khatri‐Rao product defined in the same way as the block‐wise Kronecker product, with and for n1=1 and 2.
In the case of a block PARAFAC model, (46) is replaced by
and the matrix representation (37) then becomes
with, and. Block constrained PARAFAC models were used in[70]‐[72] for modeling different types of multiuser wireless communication systems. Block constrained Tucker models were used for space‐time multiplexing MIMO‐OFDM systems[73] and for blind beamforming[74]. In these applications, the symbol matrix factor is in Toeplitz or block‐Toeplitz form.
The block tensor model defined by (45) and (46) can be viewed as a generalization of the block term decomposition introduced in[75] for third‐order tensors that are decomposed into a sum of P Tucker models of rank‐ (L,M,N), which corresponds to the particular case where all the factor matrices are full column rank, with,,, for p=1,…,P,, and each sub‐tensor is decomposed by means of its HOSVD.
A third‐order block PARALIND/CONFAC model is visualized in Figure2. This figure is to be compared with Figure five in[76] representing a block term decomposition of a third‐order tensor into rank‐ (L p ,M p ,N p ) terms, when each term has a PARALIND/CONFAC structure.
1.3.5 PARALIND/CONFAC‐ (N1,N) models
Now, we introduce a variant of PARALIND/CONFAC models that we shall call PARALIND/CONFAC‐ (N1,N) models. This variant corresponds to PARALIND/CONFAC models (42) with only N1 constrained matrix factors, which implies R n =R and for n=N1+1,…,N
In[77], a block PARALIND/CONFAC‐(2,3) model that can be deduced from (49) was used for modeling uplink multiple‐antenna code division multiple access (CDMA) multiuser systems.
The block term decomposition (BTD) in rank‐ (1,L p ,L p ) terms of a third‐order tensor, which is compared to a third‐order PARATREE model in[78], can also be viewed as a particular CONFAC‐(1,3) model. Indeed, such a decomposition can be written as[79]
where the matrices and are rank‐ L p , and. Defining,, and, with, it is easy to verify that the BTD (50) can be rewritten as the following CONFAC‐(1,3) model:
with the constraint matrix
1.3.6 PARATUCK models
A PARATUCK‐ (N1,N) model for a N th‐order tensor, with N>N1, is defined in scalar form as follows[66, 67]:
where and are entries of the factor matrix and of the interaction/allocation matrix, respectively, and is the (N-1)th‐order input tensor. Defining the core tensor element‐wise as
the PARATUCK‐ (N1,N) model can be rewritten as a Tucker‐ (N1,N) model (29)‐(30).
Defining the allocation/interaction tensor of order N1+1, such as
the core tensor can then be written as the Hadamard product of the tensors
can then be written as the Hadamard product of the tensors and
and along their first N1 modes
along their first N1 modes
1.3.6.0 Remarks
-
The PARATUCK‐ (N 1,N) model can be interpreted as the transformation of the input tensor
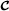 via its multiplication by the factor matrices A(n),n=1,…,N1, along its first N1 modes, combined with a mode‐n resource allocation (n=1,…,N1) relatively to the mode‐ (N1+1) of the transformed tensor
via its multiplication by the factor matrices A(n),n=1,…,N1, along its first N1 modes, combined with a mode‐n resource allocation (n=1,…,N1) relatively to the mode‐ (N1+1) of the transformed tensor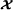 , by means of the allocation matrices Φ(n).
, by means of the allocation matrices Φ(n). -
In telecommunications applications, the output modes will be called diversity modes because they correspond to time, space, and frequency diversities, whereas the input modes are associated with resources like transmit antennas, codes, and data streams. For these applications, the matrices Φ(n) are formed with 0’s and 1’s, and they can be interpreted as allocation matrices used for allocating some resources r n to the output mode‐ (N1+1). Another way to take resource allocations into account consists in replacing the N1 allocation matrices Φ(n) by the (N1+1)th‐order allocation tensor defined in (53).
-
Special cases:
-
For N1=2 and N=3, we obtain the standard PARATUCK‐2 model introduced in[59]. (52) then becomes
(55)The allocation tensor
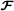 defined in (53) can be rewritten as(56)
defined in (53) can be rewritten as(56)which corresponds to a PARAFAC model with matrix factors (). The PARATUCK‐2 model (55) can then be viewed as a Tucker‐2 model with the core tensor given by the Hadamard product of and along their common modes {r1,r2}
This combination of a Tucker‐2 model for
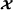 with a PARAFAC model for
with a PARAFAC model for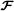 gave rise to the name PARATUCK‐2. The constraint matrices (Φ(1),Φ(2)) define interactions between columns of the factor matrices (A(1),A(2)), along the mode‐3 of
gave rise to the name PARATUCK‐2. The constraint matrices (Φ(1),Φ(2)) define interactions between columns of the factor matrices (A(1),A(2)), along the mode‐3 of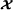 , while the matrix C contains the weights of these interactions.
, while the matrix C contains the weights of these interactions. -
For N1=2 and N=4, we obtain the PARATUCK‐(2,4) model introduced in[66]
(57)As for the PARATUCK‐2 model, the PARATUCK‐(2,4) can be viewed as a combination of a Tucker‐(2,4) model with a core tensor given by the Hadamard product of the tensors and along their common modes {r1,r2}
with the same allocation tensor
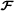 defined in (56).
defined in (56).
-
1.3.7 Rewriting of PARATUCK models as constrained PARAFAC models
This rewriting of PARATUCK models as constrained PARAFAC models can be used to deduce both matrix unfoldings by means of the general formula (37) and sufficient conditions for essential uniqueness of such PARATUCK models, as will be shown in Section 1.4.
1.3.7.0 Link between PARATUCK‐(2,4) and constrained PARAFAC‐4 models
We now establish the link between the PARATUCK‐(2,4) model (57) and the fourth‐order constrained PARAFAC model
whose matrix factors (,,,), and constraint matrices (Ψ(1),Ψ(2)) acting on the original factors (A(1),A(2)), are given by
where is a mode‐3 unfolded matrix of the tensor.
Proof.
See Appendix 5.
1.3.7.0 Remarks
-
Application of the formula (38) to the constrained PARAFAC model (58), with the matrix factors, gives the following flat mode‐1 and mode‐2 matrix unfoldings for the PARATUCK‐(2,4) model (57)
-
The constrained PARAFAC‐4 model (58)‐(60) can be written in mode‐n product notation as
(61) -
Defining the core tensor as
(62) -
the constrained PARAFAC‐4 model can also be viewed as the following Tucker‐(2,4) model
(63) -
It can also be viewed as a CONFAC‐(2,4) model with matrix factors (A(1),A(2),F,D), and constraint matrices Ψ(1) and Ψ(2) defined in (60).
-
Choosing and, the matrix unfolding (37) of the PARAFAC model (61) is given by
(64)Proof.Using the identity (90) gives
(65)Replacing Ψ(1) and Ψ(2) by their expressions (102) and (103) leads to
(66)which implies
(67)and consequently (64) can be deduced.
This equation can also be obtained from the equivalent Tucker‐(2,4) model (62)‐(63) as
(68)with
Using the identity (66), we obtain
(69)and replacing by its expression (69) into (68) gives (64).
-
When the allocation matrices and the input tensor
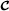 are known, the matrix factors can be estimated through the LS estimation of their Kronecker product using the matrix unfolding (64).
are known, the matrix factors can be estimated through the LS estimation of their Kronecker product using the matrix unfolding (64). -
The product in (57) can be replaced by, which amounts to replace the allocation matrices Φ(1) and Φ(2) by the third‐order allocation tensor, the matrix being equivalent to, i.e., a mode‐1 flat matrix unfolding of the allocation tensor
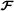 .
.
1.3.7.0 Link between PARATUCK‐2 and constrained PARAFAC‐3 models
By proceeding in the same way as for the PARATUCK‐(2,4) model, it is easy to show that the PARATUCK‐2 model (55) is equivalent to a third‐order constrained PARAFAC model whose matrix factors,, and, with R=R1R2, are given by
with the same constraint matrices Ψ(1) and Ψ(2) defined in (60).
By analogy with the PARATUCK‐(2,4) model, (61), (63), and (64) become for the PARATUCK‐2 model
with the core tensor defined as
and
1.3.7.0 Remarks
-
Note that (71) and (72) allow interpreting the PARATUCK‐2 model as a Tucker‐(2,3) model, defined in (31)‐(32). If we choose, for k=1 and 2 and define the allocation tensor such as, the PARATUCK‐2 model (55) becomes the following Tucker‐(2,3) model:
-
and the associated constrained PARAFAC‐3 model can be deduced from (70)
-
with the same constraint matrices Ψ(1) and Ψ(2) as those defined in (60). A block Tucker‐(2,3) model transformed into a block constrained PARAFAC‐3 model was used in[72] for modeling in a unified way three multiuser wireless communication systems.
-
Now, we show the equivalence of the expressions (72) and (54) of the core tensor. Applying the formula (38) to the PARAFAC model (72) gives
(73) -
Using the identity (66) in (73) gives.
-
For the formula (54), with N=3 and N1=2, we have
-
or equivalently in terms of matrix Hadamard product
-
with, and, which gives
-
and consequently, showing the equivalence of the two core tensor expressions (72) and (54).
1.3.7.0 Link between PARATUCK‐ (N- 2,N) and constrained PARAFAC‐ N models
Let us consider the PARATUCK‐ (N1,N) model (52) in the case N1=N-2
and let us define the change of variables corresponding to a combination of the N1 modes associated with the constraints/allocations. Then, (74) can be written as the following constrained PARAFAC‐N model:
with the following matrix factors
where is a mode‐ (N1+1) unfolded matrix of the tensor, and the constraint matrices are given in (94) as
The constrained PARAFAC model (75) can also be written as a Tucker‐ (N1,N) model (30) with the core tensor defined in (54) or, equivalently,
1.3.8 Comparison of constrained tensor models
To conclude this presentation, we compare the so‐called CONFAC‐ (N1,N) and PARATUCK‐ (N1,N) constrained tensor models, introduced in this paper with a resource allocation point of view. Due to the PARAFAC structure (41) of the core tensor of CONFAC models, each element of the output tensor is the sum of R components as shown in (43). Moreover, due to the special structure of the allocation matrices Φ(n) whose columns are unit vectors, each component r is the result of a combination of N resources, under the form of the product, the N resources being fixed by the allocation matrices.
is the sum of R components as shown in (43). Moreover, due to the special structure of the allocation matrices Φ(n) whose columns are unit vectors, each component r is the result of a combination of N resources, under the form of the product, the N resources being fixed by the allocation matrices.
With the CONFAC‐ (N1,N) model (49), each component r is a combination of N1 resources determined by the allocation matrices for n=1,…,N1.
There are two main differences between the PARATUCK‐ (N1,N) models (52) and the CONFAC models (42). The first one is that the allocation matrices of PARATUCK models, formed with 0’s and 1’s, have not necessarily unit vectors as column vectors, which means that it is possible to allocate resources r
n
to the (N1+1)th mode of the output tensor . The second one results from the interpretation of PARATUCK‐ (N1,N) models as Tucker‐ (N1,N) models, implying that each element of
. The second one results from the interpretation of PARATUCK‐ (N1,N) models as Tucker‐ (N1,N) models, implying that each element of is equal to the sum of terms, where is an entry of the allocation tensor
is equal to the sum of terms, where is an entry of the allocation tensor defined in (53), each term being a combination of resources under the form of products. Moreover, in telecommunication applications, the input tensor
defined in (53), each term being a combination of resources under the form of products. Moreover, in telecommunication applications, the input tensor can be used as a code tensor.
can be used as a code tensor.
Another way to compare PARALIND/CONFAC and PARATUCK models is in terms of dependencies/interactions between their factor matrices. In the case of PARALIND/CONFAC models, as pointed out by (42), the constraint matrices act independently on each factor matrix, expliciting linear dependencies between columns of these matrices. For PARATUCK models, their writing as Tucker‐ (N1,N) models with the core tensor defined in (54) allows to interpret the tensor as an interaction tensor which defines interactions between N1 factor matrices, the tensor
as an interaction tensor which defines interactions between N1 factor matrices, the tensor providing the strength of these interactions.
providing the strength of these interactions.
The main constrained PARAFAC models are summarized in Tables1 and2.
1.4 Uniqueness issue
Several results exist for essential uniqueness of PARAFAC models, i.e., uniqueness of factor matrices up to column permutation and scaling. These results concern both deterministic and generic uniqueness, i.e., uniqueness for a particular PARAFAC model or uniqueness with probability one in the case where the entries of the factor matrices are drawn from continuous distributions. An overview of main uniqueness conditions of PARAFAC models of third‐order tensors can be found in[80] for the deterministic case and in[81] for the generic case. Hereafter, we briefly summarize some basic results on uniqueness of PARAFAC models. The case with linearly dependent loadings is also discussed. Then, we present new results concerning the uniqueness of PARATUCK models. These results are directly deduced from sufficient conditions for essential uniqueness of their associated constrained PARAFAC models, as established in the previous section. As these conditions involve the notion of k‐rank of a matrix, we first recall the definition of k‐rank.
Definition of k‐rank
The k‐rank (also called Kruskal’s rank) of a matrix, denoted by k A , is the largest integer such that any set of k A columns of A is linearly independent.
It is obvious that k A ≤r A .
1.4.1 Uniqueness of PARAFAC‐ N models[82]
The PARAFAC‐N model (33)‐(35) is essentially unique, i.e., its factor matrices, are unique up to column permutation and scaling, if
Essential uniqueness means that two sets of factor matrices are linked by the following relations, for n=1,…,N, where Π is a permutation matrix and Λ(n) are non‐singular diagonal matrices such as.
In the generic case, the factor matrices are full rank, with, and Kruskal’s condition (76) becomes
Case of third‐order PARAFAC models. Consider a third‐order tensor of rank R, satisfying a PARAFAC model with matrix factors (A,B,C). Kruskal’s condition (76) becomes
1.4.1.0 Remarks
-
The condition (76) is sufficient but not necessary for essential uniqueness. This condition does not hold when R=1. It is also necessary for R=2 and R=3 but not for R>3 (see[83]).
-
The first sufficient condition for essential uniqueness of third‐order PARAFAC models was established by Harshman[84] and then generalized by Kruskal[52] using the concept of k‐rank. A more accessible proof of Kruskal’s condition is provided in[85]. Kruskal’s condition was extended to complex‐valued tensors in[15] and to N‐way arrays, with N>3, in[82].
-
Necessary and sufficient uniqueness conditions more relaxed than the Kruskal’s one were established for third‐ and fourth‐order tensors, under the assumption that at least one matrix factor is full column rank[86, 87]. These conditions are complicated to apply. Other more relaxed conditions have been derived independently by Stegeman[88] and Guo et al.[89], for third‐order PARAFAC models with a full column rank matrix factor.
-
From the condition (78), we can conclude that if two matrix factors (A and B) are full column rank (k A =k B =R), then the PARAFAC model is essentially unique if the third matrix factor (C) has no proportional columns (k C >1).
-
If one matrix factor (C for instance) is full column rank, then (78) gives
(79) -
In[88] and[89], it is shown that the PARAFAC model (A,B,C), with C of full column rank, is essentially unique if the other two matrix factors A and B satisfy the following conditions:
(80) -
Conditions (80) are more relaxed than (79). Indeed, if for instance k A =2 and r A =k A +δ with δ>0, application of (79) implies k B =R, i.e., B must be full column rank, whereas (80) gives k B ≥R-δ which does not require that B be full column rank.
-
When one matrix factor (C for instance) is known and Kruskal’s condition (78) is satisfied, as it is often the case in telecommunication applications, essential uniqueness is ensured without permutation ambiguity and with only scaling ambiguities (Λ A ,Λ B ) such as Λ A Λ B =I R .
1.4.2 Uniqueness of PARAFAC models with linearly dependent loadings
If one matrix factor contains at least two proportional columns, i.e., its k‐rank is equal to one, then Kruskal’s condition (78) cannot be satisfied. In this case, partial uniqueness can be ensured, i.e., some columns of some matrix factors are essentially unique while the others are unique up to multiplication by a non‐singular matrix[90]. To illustrate this result, let us consider the case of the PARAFAC model of a fourth‐order tensor with factor matrices (A,B,C,D) whose two of them have two identical columns at the same position
with  . We have k
A
=k
B
=1, and consequently, the uniqueness condition (76) for N=4 becomes k
C
+k
D
≥2R+1, which cannot be satisfied. In this case, we have partial uniqueness. Indeed, the matrix slices (40) can be developed as follows:
. We have k
A
=k
B
=1, and consequently, the uniqueness condition (76) for N=4 becomes k
C
+k
D
≥2R+1, which cannot be satisfied. In this case, we have partial uniqueness. Indeed, the matrix slices (40) can be developed as follows:
From this expression, it is easy to conclude that the last two columns of C and D are unique up to a rotational indeterminacy. Indeed, if one replaces the matrices (C2,D2) by, where is a non‐singular matrix, the matrix slices Xi j.. remain unchanged. So, the PARAFAC model is said partially unique in the sense that only the blocks (A1,B1,C1,D1) are essentially unique, the blocks C2 and D2 being unique up to a non‐singular matrix. Essential uniqueness means that any alternative blocks () are such as, where Π is a permutation matrix and Δ a , Δ b , Δ c , and Δ d are diagonal matrices such as Δ a Δ b Δ c Δ d =IR-2. In[91], sufficient conditions are provided for essential uniqueness of fourth‐order PARAFAC models with one full column rank factor matrix and at most three collinear factor matrices, i.e., having one (or more) column(s) proportional to another column. Note that this type of model can be interpreted as a fourth‐order CONFAC model with constraints on at most three matrix factors. Uniqueness is ensured if any pair of proportional columns cannot be common to two collinear factors, which is not the case of the example above due to the fact that the two equal columns of A and B are in the same position.
The PARALIND and CONFAC models represent a class of constrained PARAFAC models where the columns of one or more matrix factors are linearly dependent or collinear. In the case of CONFAC models, such a collinearity takes the form of repeated columns, the repetitions being explicitly modeled by means of constraint matrices. The work[92] derived both essential uniqueness conditions and partial uniqueness conditions for PARALIND/CONFAC models of third‐order tensors. Therein, the relation with uniqueness of constrained Tucker3 models and the block decomposition in rank‐(L,L,1) terms is also discussed. The essential uniqueness condition for a given matrix factor in PARALIND models makes use of Kruskal’s permutation lemma[52, 86].
Consider a third‐order tensor satisfying a PARALIND model with matrix factors (A,B,C) and constraint matrices Φ(i), i=1,2,3. Suppose and A have full column rank and let ω(·) denote the number of nonzero elements of its vector argument. Define, i=1,…,R1. If for any vector d
then A is essentially unique[92]. The uniqueness condition for B and C is analogous to condition (81) by interchanging the roles of Φ(1), Φ(2), and Φ(3).
When PARALIND model reduces to PARAFAC model, condition (81) is identical to Condition B of[86] for the essential uniqueness of the PARAFAC model in the case of a full column rank matrix factor. More recently in[93], improved versions of the main uniqueness conditions of PARALIND/CONFAC models have been derived. The results presented therein involve simpler proofs than those of[92]. Moreover, the associated uniqueness conditions are easy to check in comparison with the ones presented earlier in[92].
In[94], a ‘uni‐mode’ uniqueness condition is derived for a PARAFAC model with linearly dependent (proportional/identical) columns in one matrix factor. This condition is particularly useful for a subclass of PARALIND/CONFAC models with, i.e., when collinearity is confined within the first matrix factor. Let, where contains collinear columns, the collinearity pattern being captured by Φ(1). Assuming that does not contain an all‐zero column, if
then A is essentially unique. Generalizations of this condition can be obtained by imposing additional constraints on the ranks and k‐ranks of the matrix factors (see[94] for details).
1.4.3 Uniqueness of Tucker models
Contrary to PARAFAC models, the Tucker ones are generally not essentially unique. Indeed, the parameters of Tucker models can be only estimated up to non‐singular transformations characterized by non‐singular matrices T(n) that act on the mode‐n matrix factors A(n) and can be cancelled in replacing the core tensor by. This result is easy to verify by applying the property (13) of mode‐n product
Uniqueness can be obtained by imposing some constraints on the core tensor or the matrix factors (see[9] for a review of main results concerning uniqueness of Tucker models, with discussion of three different approaches for simplifying core tensors so that uniqueness is ensured). Uniqueness can also result from a core with information redundancy and structure constraints as in[33] where the core is characterized by matrix slices in Hankel and Vandermonde forms.
1.4.4 Uniqueness of the PARATUCK‐(2,4) model
Let us consider the PARATUCK‐(2,4) model defined by (57), with matrix factors A(1) and A(2), constraint matrices Φ(1) and Φ(2) and core tensor . As previously shown, this model is equivalent to the constrained PARAFAC model (58) whose matrix factors are
. As previously shown, this model is equivalent to the constrained PARAFAC model (58) whose matrix factors are
with Ψ(1) and Ψ(2) defined in (60). Due to the repetition of some columns of A(1) and A(2) and assuming that these matrices do not contain an all‐zero column, we have k A =k B =1, and application of Kruskal’s condition (76), with N=4, gives
which can never be satisfied. However, more relaxed sufficient conditions can be established for essential uniqueness of the PARATUCK‐(2,4) model. For that purpose, we consider the contracted constrained PARAFAC model obtained by combining the first two modes and using (67), which leads to a third‐order PARAFAC model with matrix factors
Note that uniqueness of the matrix factors of the contracted PARAFAC model (83) implies uniqueness of the matrix factors A(1) and A(2) of the original PARATUCK‐(2,4) model. This comes from the fact that A(1) and A(2) can be recovered (up to a scaling factor) from their Kronecker product[95]. Application of the conditions (80) to the contracted PARAFAC model (83) allows deriving the following theorem.
1.4.4.0 Theorem
The PARATUCK‐(2,4) model defined by (57) is essentially unique
-
1) When A(1) and A(2) are full column rank ()
-
If and
-
2) When (Φ(1)◇Φ(2))T is full column rank
-
If and
-
3) When is full column rank
-
If and
In[67], an application of the PARATUCK‐(2,4) model to tensor space‐time (TST) coding is considered. Therein, the matrix factors A(1) and A(2) represent the symbol and channel matrices to be estimated, while the constraint matrices Φ(1) and Φ(2) play the role of allocation matrices of the transmission system, and the tensor is the coding tensor. In this context, Φ(1), Φ(2), and
is the coding tensor. In this context, Φ(1), Φ(2), and can be properly designed to satisfy the sufficient conditions of item 1) of the theorem.
can be properly designed to satisfy the sufficient conditions of item 1) of the theorem.
The sufficient conditions of this theorem can easily be extended to the case of PARATUCK‐(N1,N) models in replacing A(1)⊗A(2), Φ(1)◇Φ(2),, and R1R2, by,,, and, respectively.
2 Conclusions
Several tensor models among which some are new have been presented in a general and unified framework. The use of the index notation for mode combination based on Kronecker products provides an original and concise way to derive vectorized and matricized forms of tensor models. A particular focus on constrained tensor models has been made with a perspective of designing MIMO communication systems with resource allocation. A link between PARATUCK models and constrained PARAFAC models has been established, which allows to apply results concerning PARAFAC models to derive uniqueness properties and parameter estimation algorithms for PARATUCK models. In a companion paper, several tensor‐based MIMO systems are presented in a unified way based on constrained PARAFAC models, and a new tensor‐based space‐time‐frequency (TSTF) MIMO transmission system with a blind receiver is proposed using a generalized PARATUCK model[96]. Even if this presentation of constrained tensor models has been made with the aim of designing MIMO transmission systems, we believe that such tensor models can be applied to other areas than telecommunications, like for instance biomedical signal processing, and more particularly for ECG and EEG signals modeling, with spatial constraints allowing to take into account the relative weight of the contributions of different areas of surface to electrodes. The considered constrained tensor models allow to take constraints into account either independently on each matrix factor of a PARAFAC decomposition, in the case of PARALIND/CONFAC models, or between factors, in the case of PARATUCK models. A perspective of this work is to consider constraints into tensor networks which decompose high‐order tensors into lower‐order tensors for big data processing[97]. In this case, the constraints could act either separately on each tensor component to facilitate their physical interpretability or between tensor components to explicit their interactions.
Appendices
Appendix 1
Some matrix formulae
For,,, and, n=1,…,N
For, n=1,…,N, and, p=1,…,P
In particular, for,,,,,,,,, and, we have
Appendix 2
Tensor extension of a matrix
Following the same demonstration as for (21) and (22), it is easy to deduce the following more general formula for the extension of into a tensor such as. Defining, we have
Similarly, for the extension of into a tensor such as, we have
where.
For instance, if we consider the following tensor extension of
the combination of formulae (94) and (95) gives
which can be written as
with Ψ1=1 MN ⊗I I and.
Appendix 3
Proof of (27)
Defining () and () as the sets of indices i n and r n associated respectively with the sets () of index n, the formula (20) allows writing the element of the core tensor as
where and. Substituting and by their expressions (24) and (97) into (19) gives
Applying the general Kronecker formula (17) in terms of the index notation allows to rewrite this matrix unfolding as
Appendix 4
Proof of (37)
Substituting the expression (34) of into (19) and using the identities (14) and (15) give
which ends the proof of (37).
Appendix 5
Proof of (59) and (60)
Let us define the third‐order tensors,,, and such as
The tensor model (57) can be rewritten as
Defining the change of variables r=(r1-1)R2+r2 that corresponds to a combination of the last two modes of the tensors ,
, ,
, , and
, and , (101) can be rewritten as the constrained PARAFAC‐4 model (58), where,,, and are entries of mode‐1 matrix unfoldings of the tensors
, (101) can be rewritten as the constrained PARAFAC‐4 model (58), where,,, and are entries of mode‐1 matrix unfoldings of the tensors ,
, ,
, , and
, and , i.e., entries of,,, and, respectively. Using the formulae (21) and (22), we can directly deduce the following expressions of A and B:
, i.e., entries of,,, and, respectively. Using the formulae (21) and (22), we can directly deduce the following expressions of A and B:
For the matrix F, using the index notation with the definition (100) gives
Applying the formula (16), we directly obtain
References
McCullagh P: Tensor Methods in Statistics. Chapman and Hall, New York; 1987.
Comon P: Tensor decompositions: state of the art and applications. In Mathematics in Signal Processing V. Edited by: McWhirter JG, Proudler IK. Clarendon Press,, Oxford; 2002:1-24.
Tucker LR: Some mathematical notes on three‐mode factor analysis. Psychometrika 1966, 31: 279-311.
Harshman RA: Foundations of the PARAFAC procedure: model and conditions for an “explanatory” multimodal factor analysis. UCLA Working Pap. Phon 1970, 16: 1-84.
Carroll JD, Chang J: Analysis of individual differences in multidimensional scaling via an N‐way generalization of “Eckart‐Young” decomposition. Psychometrika 1970, 35(3):283-319.
Kiers HAL: Towards a standardized notation and terminology in multiway analysis J. Chemometrics 2000, 14(2):105-122.
Kroonenberg PM: Applied Multiway Data Analysis. Wiley, Hoboken; 2008.
Bro R: Multi‐way analysis in the food industry: models, algorithms and applications. Ph.D. dissertation, University of Amsterdam, Amsterdam 1998.
Smilde A, Bro R, Geladi P: Multi‐way Analysis: Applications in the Chemical Sciences. Wiley, Chichester; 2004.
Cardoso J‐F: Eigen‐structure of the fourth‐order cumulant tensor with application to the blind source separation problem. In Proc. of IEEE ICASSP’90. Albuquerque; 1990:2655-2658.
Cardoso J‐F, Comon P: Tensor‐based independent component analysis. In Proc. of EUSIPCO’90. Barcelona; 1990:673-676.
Cardoso J‐F: Super‐symmetric decomposition of the fourth‐order cumulant tensor: blind identification of more sources than sensors. In Proc. of IEEE ICASSP’91. Toronto; 1991:3109-3112.
De Lathauwer L: Signal processing based on multilinear algebra. Ph.D. dissertation, KU Leuven, Leuven 1997.
Comon P, Jutten C: Handbook of Blind Source Separation. Independent Component Analysis and Applications. Elsevier, Oxford; 2010.
Sidiropoulos ND, Giannakis GB, Bro R: Blind PARAFAC receivers for DS‐CDMA systems. IEEE Trans. Signal Process 2000, 48(3):810-823.
Cichocki A, Zdunek R, Phan AH, Amari S‐I: Nonnegative Matrix and Tensor Factorizations. Applications to Exploratory Multi‐way Data Analysis and Blind Source Separation. Wiley, Chichester; 2009.
Kolda TG, Bader BW: Tensor decompositions and applications. SIAM J. Matrix Anal. Appl 2009, 51(3):455-500.
Acar E, Yener B: Unsupervised multiway data analysis: a literature survey. IEEE Trans. Knowledge Data Eng 2009, 21(1):6-20.
Morup M: Applications of tensor (multiway array) factorizations and decompositions in data mining. In Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. Wiley,, Chichester; 2011:24-40.
Sorensen M, De Lathauwer L, Comon P, Icart S, Deneire L: Canonical polyadic decomposition with a columnwise orthonormal factor matrix. SIAM J. Matrix Anal. Appl 2012, 33(4):1190-1213.
Shashua A, Hazan T: Non‐negative tensor factorization with applications to statistics and computer vision. In Proc. of 22nd Int. Conf. on Machine Learning. Bonn; 2005:792-799.
Hazan S, Polak S, Shashua A: Sparse image coding using a 3D non‐negative tensor factorization. In Proc. of 10th IEEE Int. Conf. on Computer Vision (ICCV’ 2005). Beijing; 2005:50-57.
Friedlander MP, Hatz K: Computing nonnegative tensor factorizations. Optim. Meth. Software 2008, 23(4):631-647.
Zhang Q, Wang H, Plemmons R, Pauca P: Tensor methods for hyperspectral data processing: a space object identification study. J. Opt. Soc. Am. A 2008, 25(12):3001-3012.
Benetos E, Kotropoulos C: Non‐negative tensor factorization applied to music genre classification. IEEE Trans. Audio, Speech, Language Proc 2010, 18(8):1955-1967.
Ozerov A, Févote C, Blouet R, Durrieu G: Multichannel nonnegative tensor factorization with structured constraints for user‐guided audio source separation. In Proc. of ICASSP’ 2011. Prague; 2011.
Acar E, Dunlavy DM, Kolda TG, Morup M: Scalable tensor factorizations with missing data. In Proc. of 10th SIAM Int. Conf. on Data Mining. Columbus; 2010:701-712.
Royer J‐P, Thirion‐Moreau N, Comon P: Computing the polyadic decomposition of nonnegative third order tensors. Signal Process 2011, 91: 2159-2171.
Phan A‐H, Cichocki A: Extended HALS algorithm for nonnegative Tucker decomposition and its applications for multiway analysis and classification. Neurocomputing 2011, 74: 1956-1969.
Welling M, Weber M: Positive tensor factorization. Pattern Recogn. Lett 2001, 22(12):1255-1261.
Morup M, Hansen LK: Algorithms for sparse non‐negative Tucker decompositions. Neural Comput 2008, 20: 2112-2131.
Favier G, Bouilloc T: A constrained tensor based approach for MIMO NL‐CDMA systems. In Proc. of EUSIPCO’ 2010. Aalborg; 2010.
Favier G, Bouilloc T, de Almeida ALF: Blind constrained block‐Tucker2 receiver for multiuser SIMO NL‐CDMA communication systems. Signal Process 2012, 92(7):1624-1636.
Favier G, Kibangou AY, Bouilloc T: Nonlinear system modeling and identification using Volterra‐PARAFAC models. Int. J. of Adaptive Control and Sig. Proc 2012, 26: 30-53.
Bouilloc T, Favier G: Nonlinear channel modeling and identification using bandpass Volterra‐PARAFAC models. Signal Process 2012, 92(6):1492-1498.
Kibangou AY, Favier G: Identification of parallel‐cascade Wiener systems using joint diagonalization of third‐order Volterra kernel slices. IEEE Signal Proc. Lett 2009, 16(3):188-191.
Favier G: Nonlinear system modeling and identification using tensor approaches. In Proc. of 10th Int. Conf. on Sciences and Techniques of Automatic Control and Computer Engineering (STA’ 2009). Hammamet; 2009.
Fernandes CER, Favier G, Mota JCM: Blind channel identification algorithms based on the Parafac decomposition of cumulant tensors: the single and multiuser cases. Signal Process 2008, 88: 1382-1401.
Fernandes CER, Favier G, Mota JCM: Parafac‐based blind identification of convolutive MIMO linear systems. In Proc. of 15th IFAC Symp. on System Identification (SYSID’ 2009). Saint‐Malo; 2009.
Brachat J, Comon P, Mourrain B, Tsigaridas E: Symmetric tensor decomposition. Lin. Algebra Appl 2010, 433(11–12):1851-1872.
Nion D, De Lathauwer L: A block component model‐based blind DS‐CDMA receiver. IEEE Trans. Signal Proc 2008, 56(11):5567-5579.
Kibangou AY, Favier G: Non‐iterative solution for PARAFAC with a Toeplitz matrix factor. In Proc. of EUSIPCO’ 2009. Glasgow; 2009:691-695.
Sorensen M, De Lathauwer L: Blind signal separation via tensor decomposition with Vandermonde factor: canonical polyadic decomposition. IEEE Trans. Signal Process 2013, 61(22):5507-5519.
Goulart JH, Favier G: An algebraic solution for the Candecomp/PARAFAC decomposition with circulant factors. SIAM J. Matrix Analysis and Appl 2014. http://hal.archives-ouvertes.fr/docs/00/96/72/63/PDF/RR-2014-02_I3S.pdf
Comon P, Sorensen M, Tsigaridas E: Decomposing tensors with structured matrix factors reduces to rank‐1 approximations. In Proc. of IEEE ICASSP’ 2010. Dallas; 2010:14-19.
Sorensen M, Comon P: Tensor decompositions with banded matrix factors. Lin. Algebra Appl 2013, 438: 919-941.
Carroll JD, Pruzansky S, Kruskal JB: Candelinc: a general approach to multidimensional analysis of many‐way arrays with linear constraints on parameters. Psychometrika 1980, 45(1):3-24.
Pollock DSG: On Kronecker products, tensor products and matrix differential calculus, Working paper 11/34. Univ.of Leicester, Dept. of Economics, UK 2011. http://www.le.ac.uk/ec/research/RePEc/lec/leecon/dp11-34.pdf
De Lathauwer L, De Moor B, Vandewalle J: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl 2000, 21(4):1253-1278.
Cattell RB: “Parallel proportional profiles” and other principles for determining the choice of factors by rotation. Psychometrika 1944, 9: 267-283.
Hitchcock FL: The expression of a tensor or a polyadic as a sum of products. J. Math. Phys 1927, 6(3):164-189.
Kruskal JB: Three‐way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Lin. Algebra Appl 1977, 18(2):95-138.
Comon P, ten Berge JMF, De Lathauwer L, Castaing J: Generic and typical ranks of multi‐way arrays. Lin. Algebra Appl 2009, 430(11):2997-3007.
Comon P, Golub G, Lim L‐H, Mourrain B: Symmetric tensors and symmetric tensor rank. SIAM J. Matrix Anal. Appl 2008, 30(3):1254-1279.
Bro R, Kiers HAL: A new efficient method for determining the number of components in PARAFAC models. J. Chemometrics 2003, 17(5):274-286.
da Costa JPCL, Haardt M, Roemer F: Robust methods based on HOSVD for estimating the model order in PARAFAC models. In Proc. of 5th IEEE Sensor Array and Multich. Signal Proc. Workshop (SAM 2008). Darmstadt; 2008:510-514.
da Costa JPCL, Roemer F, Weis M, Haardt M: Robust R ‐D parameter estimation via closed‐form PARAFAC. In Proc. of ITG Workshop on Smart Antennas (WSA 2010). Bremen; 2010:99-106.
da Costa JPCL, Roemer F, Haardt M, de Sousa RT: Multi‐dimensional model order selection. EURASIP J. Adv. Signal Process 2011., 26:
Harshman RA, Lundy ME: Uniqueness proof for a family of models sharing features of Tucker’s three‐mode factor analysis and PARAFAC/CANDECOMP. Psychometrika 1996, 61: 133-154.
Bro R, Harshman RA, Sidiropoulos ND: Modeling multi‐way data with linearly dependent loadings, KVL tech. report 176. 2005.
Bro R, Harshman RA, Sidiropoulos ND, Lundy ME: Modeling multi‐way data with linearly dependent loadings. Chemometrics 2009, 23(7–8):324-340.
Kibangou AY, Favier G: Blind joint identification and equalization of Wiener‐Hammerstein communication channels using PARATUCK‐2 tensor decomposition. In Proc. EUSIPCO’ 2007. Poznan; Sept 2007.
Xu L, Ting J, Longxiang Y, Hongbo Z: PARALIND‐based identifiability results for parameter estimation via uniform linear array. EURASIP J. Adv. Sig. Proc 2012, 2012: 154.
Xu L, Liang G, Longxiang Y, Hongbo Z: PARALIND‐based blind joint angle and delay estimation for multipath signals with uniform linear array. EURASIP J. Adv, Sig. Proc 2012, 2012: 130.
de Almeida ALF, Favier G, Mota JCM: A constrained factor decomposition with application to MIMO antenna systems. IEEE Trans. Signal Process 2008, 56(6):2429-2442.
Favier G, da Costa MN, de Almeida ALF, Romano JMT: Tensor coding for CDMA‐MIMO wireless communication systems. In Proc. of EUSIPCO’ 2011. Barcelona; 29 Aug–2 Sept 2011.
Favier G, da Costa MN, de Almeida ALF, Romano JMT: Tensor space‐time (TST) coding for MIMO wireless communication systems. Signal Process 2012, 92(4):1079-1092.
de Almeida ALF, Favier G, Mota JCM: Space‐time spreading‐multiplexing for MIMO wireless communication systems using the PARATUCK‐2 tensor model. Signal Process 2009, 89(11):2103-2116.
de Almeida ALF, Luciani X, Stegeman A, Comon P: CONFAC decomposition approach to blind identification of underdetermined mixtures based on generating function derivatives. IEEE Trans. Signal Process 2012, 60(11):5698-5713.
de Almeida ALF, Favier G, Mota JCM: Generalized PARAFAC model for multidimensional wireless communications with application to blind multiuser equalization. In Asilomar Conf. Sig. Syst. Comp.. Pacific Grove; Nov 2005.
de Almeida ALF, Favier G, Mota JCM: PARAFAC models for wireless communication systems. In Int. Conf. on Physics in Signal and Image Processing (PSIP). Toulouse; 31 Jan–2 Feb 2005.
de Almeida ALF, Favier G, Mota JCM: PARAFAC‐based unified tensor modeling for wireless communication systems with application to blind multiuser equalization. Signal Process 2007, 87: 337-351.
de Almeida ALF, Favier G, Mota JCM: Tensor‐based space‐time multiplexing codes for MIMO‐OFDM systems with blind detection. In Proc. of 17th IEEE Symp. Pers. Ind. Mob. Radio Com. (PIMRC’ 2006). Helsinki; Sept 2006.
de Almeida ALF, Favier G, Mota JCM: Constrained Tucker‐3 model for blind beamforming. Signal Process 2009, 89: 1240-1244.
De Lathauwer L: Decompositions of a higher‐order tensor in block terms‐part II: definitions and uniqueness. SIAM J. Matrix Anal. Appl 2008, 30(3):1033-1066.
Cichocki A, Mandic D, Phan A‐H, Caiafa C, Zhou G, Zhao Q, De Lathauwer L: Tensor decompositions for signal processing applications. From two‐way to multiway component analysis. IEEE Signal Process. Mag. 2014. arXiv:1403.4462v1
de Almeida ALF, Favier G, Mota JCM: Constrained tensor modeling approach to blind multiple‐antenna CDMA schemes. IEEE Trans. Signal Process 2008, 56(6):2417-2428.
Salmi J, Richter A, Koivunen V: Sequential unfolding SVD for tensors with applications in array signal processing. IEEE Trans. Signal Process 2009, 57(12):4719-4733.
de Lathauwer L: Blind separation of exponential polynomials and the decomposition of a tensor in rank‐( L r , L r , 1) terms. SIAM J. Matrix Anal. Appl 2011, 32(4):1451-1474.
Domanov I, De Lathauwer L: On the uniqueness of the canonical polyadic decomposition of third‐order tensors—part I: basic results and uniqueness of one factor matrix. SIAM. J. Matrix Anal. & Appl 2013, 34(3):855-875. arXiv:1301.4602v1
Domanov I, De Lathauwer L: Generic uniqueness conditions for the canonical polyadic decomposition and INDSCAL. arXiv:1405.6238v1, (KU Leuven, Belgium, 2014)
Sidiropoulos ND, Bro R: On the uniqueness of multilinear decomposition of N‐way arrays. J. Chemometrics 2000, 14: 229-239.
ten Berge JMF, Sidiropoulos ND: On uniqueness in CANDECOMP/PARAFAC. Psychometrika 2002, 67(3):399-409.
Harshman RA: Determination and proof of minimum uniqueness conditions for PARAFAC1. UCLA Working Pap. Phon 1972, 22: 111-117.
Stegeman A, Sidiropoulos ND: On Kruskal’s uniqueness condition for the CANDECOMP/PARAFAC decomposition. Lin. Algebra Appl 2007, 420: 540-552.
Jiang T, Sidiropoulos ND: Kruskal’s permutation lemma and the identification of CANDECOMP/PARAFAC and bilinear models with constant modulus constraints. IEEE Trans. Signal Process 2004, 52(9):2625-2636.
De Lathauwer L: A link between the canonical decomposition in multilinear algebra and simultaneous matrix diagonalization. SIAM J. Matrix Anal. Appl 2006, 28(3):642-666.
Stegeman A: On uniqueness conditions for CANDECOMP/PARAFAC and INDSCAL with full column rank in one mode. Lin. Algebra Appl 2008, 431(1–2):211-227.
Guo X, Miron S, Brie D, Zhu S, Liao X: A CANDECOMP/PARAFAC perspective on uniqueness of DOA estimation using a vector sensor array. IEEE Trans. Signal Process 2011, 59(7):3475-3481.
Ten Berge JMF: Partial uniqueness in CANDECOMP/PARAFAC. J. Chemometrics 2004, 18: 12-16.
Brie D, Miron S, Caland F, Mustin C: An uniqueness condition for the 4‐way CANDECOMP/PARAFAC model with collinear loadings in three modes. In Proc. of IEEE ICASSP’ 2011. Prague; May 2011.
Stegeman A, de Almeida ALF: Uniqueness conditions for constrained three‐way factor decompositions with linearly dependent loadings. SIAM J. Matrix Anal. Appl 2009, 31(3):1469-1490.
Stegeman A, Lam TTT: Improved uniqueness conditions for canonical tensor decompositions with linearly dependent loadings. SIAM J. Matrix Anal. Appl 2012, 33(4):1250-1271.
Guo X, Miron S, Brie D, Stegeman A: Uni‐mode and partial uniqueness conditions for CANDECOMP/PARAFAC of three‐way arrays with linearly dependent loadings. SIAM J. Matrix Anal. Appl 2012, 33(1):111-129.
Van Loan CF, Pitsianis N: Linear Algebra for Large Scale and Real‐Time Applications. Edited by: Moonen MS, Golub GH, de Moor BLR. Kluwer, The Netherlands; 1993:293-293.
Favier G, de Almeida ALF: Tensor space‐time‐frequency coding with semi‐blind receivers for MIMO wireless communication systems. IEEE Trans. Signal Process 2014. in press
Cichocki A: Era of big data processing: a new approach via tensor networks and tensor decompositions. In International Workshop on Smart Info‐Media Systems in Asia (SISA‐2013). Nagoya; 30 Sept–2 Oct 2013.
Acknowledgements
This work has been developed under the FUNCAP/CNRS bilateral cooperation project (2013‐2014). André L. F. de Almeida is partially supported by CNPq. The authors are thankful to A. Cichocki for his useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Favier, G., de Almeida, A.L. Overview of constrained PARAFAC models. EURASIP J. Adv. Signal Process. 2014, 142 (2014). https://doi.org/10.1186/1687-6180-2014-142
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-6180-2014-142
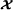 by Hitchcock[
by Hitchcock[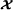 into a sum of R components, each component being a rank‐one tensor. When R is minimal in (33), it is called the rank of
into a sum of R components, each component being a rank‐one tensor. When R is minimal in (33), it is called the rank of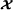 [
[

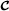 via its multiplication by the factor matrices A(n),n=1,…,N1, along its first N1 modes, combined with a mode‐n resource allocation (n=1,…,N1) relatively to the mode‐ (N1+1) of the transformed tensor
via its multiplication by the factor matrices A(n),n=1,…,N1, along its first N1 modes, combined with a mode‐n resource allocation (n=1,…,N1) relatively to the mode‐ (N1+1) of the transformed tensor , by means of the allocation matrices Φ(n).
, by means of the allocation matrices Φ(n). defined in (53) can be rewritten as
defined in (53) can be rewritten as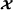 with a PARAFAC model for
with a PARAFAC model for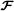 gave rise to the name PARATUCK‐2. The constraint matrices (Φ(1),Φ(2)) define interactions between columns of the factor matrices (A(1),A(2)), along the mode‐3 of
gave rise to the name PARATUCK‐2. The constraint matrices (Φ(1),Φ(2)) define interactions between columns of the factor matrices (A(1),A(2)), along the mode‐3 of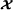 , while the matrix C contains the weights of these interactions.
, while the matrix C contains the weights of these interactions.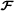 defined in (56).
defined in (56).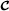 are known, the matrix factors can be estimated through the LS estimation of their Kronecker product using the matrix unfolding (64).
are known, the matrix factors can be estimated through the LS estimation of their Kronecker product using the matrix unfolding (64).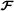 .
.