- Research
- Open access
- Published:
Distributed piecewise 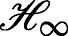 filtering design for large-scale networked nonlinear systems
filtering design for large-scale networked nonlinear systems
EURASIP Journal on Advances in Signal Processing volume 2016, Article number: 51 (2016)
Abstract
This paper investigates the problem of distributed piecewise  filtering for discrete-time large-scale nonlinear systems. The considered large-scale system is composed of a number of nonlinear subsystems and exchanges its information through communication network. Each nonlinear subsystem is described by a Takagi-Sugeno (T-S) model, and data-packet dropouts happen intermittently in communication network, and its stochastic variables are assumed to satisfy the Bernoulli random-binary distribution. Our objective is to design a distributed piecewise filter such that the filtering error system is stochastically stable with an
filtering for discrete-time large-scale nonlinear systems. The considered large-scale system is composed of a number of nonlinear subsystems and exchanges its information through communication network. Each nonlinear subsystem is described by a Takagi-Sugeno (T-S) model, and data-packet dropouts happen intermittently in communication network, and its stochastic variables are assumed to satisfy the Bernoulli random-binary distribution. Our objective is to design a distributed piecewise filter such that the filtering error system is stochastically stable with an  performance. Based on a piecewise Lyapunov function and some convexifying techniques, less conservative results are developed for the distributed piecewise
performance. Based on a piecewise Lyapunov function and some convexifying techniques, less conservative results are developed for the distributed piecewise  filtering design of the considered system in the form of linear matrix inequalities (LMIs). The effectiveness of the proposed method is validated by two examples.
filtering design of the considered system in the form of linear matrix inequalities (LMIs). The effectiveness of the proposed method is validated by two examples.
1 Introduction
In practical application, some complex systems, such as transportation systems, power systems, communication networks, and industrial processes, are referred to as large-scale systems [1, 2]. Due to strong interconnection and high dimensionality, large-scale systems lead to severe difficulties for their analysis and control synthesis. To date, three main control approaches, centralized, decentralized, and distributed control, have been proposed for large-scale systems with interconnection. Since the centralized control suffers from the excessive information processing and heavy computational burdens, there has been recently an increasing interest in the use of decentralized control for large-scale systems [3]. The decentralized control is firstly to partition the overall control problem of a large-scale system into several independent or almost independent subproblems. Then, instead of a single controller, a set of independent controllers can be designed to achieve the overall control of large-scale system [4]. However, the decentralized control strategy appears weaker stability margins and performance, especially when the interconnections among subsystems are strong [5]. In the distributed control, the supplemental feedbacks with the interconnected information are provided for the local controllers to enhance the requirements of stability and performance. As a result, the distributed control avoids those shortages appearing in both centralized and decentralized controls [6, 7].
On the other hand, an important issue is to consider the control problems of nonlinear systems because most control plants are nonlinear. Recently, Takagi-Sugeno (T-S) model has been proved to be a powerful solution to represent any smooth nonlinear functions at any preciseness [8, 9]. The T-S model employs a group of IF-THEN fuzzy rules to describe the global behavior of the nonlinear system in which a number of linear models are connected smoothly by fuzzy membership functions. T-S fuzzy approach combining the merits of both fuzzy logic theory and linear system theory is successfully implemented in embedded microprocessors and is widely applied in a variety of engineering fields [10–13]. During the past few years, a great number of results on function approximation, systematic stability analysis, controller and filtering design for T-S fuzzy systems have been reported in the open literature [14–19].
With the rapid development of digital technology, in the feedback loops, communication networks are often used instead of point-to-point connections due to their great advantages, such as simple maintenance and installation, and low cost [20–24]. Unfortunately, the network-induced imperfections, such as quantization errors, packet dropouts, and time delays, can degrade significantly the performance of control systems and may even lead to instability [25–29]. Recently, based on fuzzy/piecewise Lyapunov functions, some results on stability analysis and controller synthesis of fuzzy systems have been presented. It has been demonstrated that the inherently conservatism in common Lyapunov function can be relaxed by using piecewise/fuzzy Lyapunov functions. More recently, T-S fuzzy control has been developed to investigate large-scale nonlinear systems [30–35]. To mention a few, some results on analysis and synthesis methods for decentralized control of large-scale systems have been presented in [30–32]. In [33, 34], the decentralized  filtering problem was studied for the discrete-time large-scale system with time-varying delay. To the best knowledge of the authors, few results on the distributed
filtering problem was studied for the discrete-time large-scale system with time-varying delay. To the best knowledge of the authors, few results on the distributed  filtering design have been given for large-scale networked T-S fuzzy systems by using piecewise Lyapunov function, which motivates us for the research presented in this paper.
filtering design have been given for large-scale networked T-S fuzzy systems by using piecewise Lyapunov function, which motivates us for the research presented in this paper.
This paper will deal with the distributed  filtering problem for discrete-time large-scale nonlinear systems. The large-scale system is composed of several nonlinear subsystems and exchanges its information through communication network. Each nonlinear subsystem is described by a T-S model, and data-packet dropouts occur intermittently in communication network, and its stochastic variables satisfy the Bernoulli random-binary distribution. Based on a piecewise Lyapunov functional (PLF) and some convexifying techniques, the distributed
filtering problem for discrete-time large-scale nonlinear systems. The large-scale system is composed of several nonlinear subsystems and exchanges its information through communication network. Each nonlinear subsystem is described by a T-S model, and data-packet dropouts occur intermittently in communication network, and its stochastic variables satisfy the Bernoulli random-binary distribution. Based on a piecewise Lyapunov functional (PLF) and some convexifying techniques, the distributed  filtering design result will be proposed. It will be shown that the filtering error system is stochastically stable with an
filtering design result will be proposed. It will be shown that the filtering error system is stochastically stable with an  performance, and the filtering gains can be given by the form of LMIs. Two simulation examples will be presented to demonstrate the advantage of the proposed methods.
performance, and the filtering gains can be given by the form of LMIs. Two simulation examples will be presented to demonstrate the advantage of the proposed methods.
Notations.
\(\Re ^{n\times m}\) is the n-dimensional Euclidean space and \(\Re ^{n\times m}\) denotes the set of n×m matrices. P>0 (≥0) means that matrix P is positive definite (positive semidefinite). Sym{A} denotes \(A+A^{T}.\mathbf {I}_{n}\) and 0 m×n are the n×n identity matrix and m×n zero matrix, respectively. The subscripts n and m×n are omitted when the size is irrelevant or can be determined from the context. For matrices \(A\in \Re ^{n\times n},A^{-1}\) and A T denote the inverse and transpose of the matrix A, respectively. \(l_{2}[0,\infty)\) is the space of square-summable infinite vector sequences over \([0,\infty).\) diag{ ···} is a block-diagonal matrix. The notation \(\left \Vert \cdot \right \Vert \) denotes the Euclidean vector norm, and \(\left \Vert \cdot \right \Vert _{2}\) is the usual \(l_{2}[0,\infty)\) norm. \(\mathbb {E}\left \{ \cdot \right \} \) denotes the mathematical expectation. The notation ⋆ denotes the symmetric terms.
2 Model description and problem formulation
This paper considers a class of discrete-time large-scale systems, which consist of N nonlinear subsystems, the ith nonlinear subsystem is described by the T-S model as below.
Plant rule
 : IF
ζ
i1(t) is
: IF
ζ
i1(t) is  and ζ
i2(t) is
and ζ
i2(t) is  and ⋯ and ζ
ig
(t) is
and ⋯ and ζ
ig
(t) is  , THEN
, THEN

where \(i\in \mathcal {N}:=\{1,2,\ldots,N\}\);  denotes the lth fuzzy inference rule; r
i
is the number of fuzzy inference rules;
denotes the lth fuzzy inference rule; r
i
is the number of fuzzy inference rules;  are fuzzy sets; \(x_{i}(t)\in \Re ^{n_{xi}},y_{i}(t)\in \Re ^{n_{yi}}\), and \(z_{i}(t)\in \Re ^{n_{zi}}\) are the system state, the measured output, and the estimated signal, respectively; \(w_{i}(t)\in \Re ^{n_{wi}}\) is the disturbance input, which belongs to \(l_{2}[0,\infty);\zeta _{i}(t):=[\zeta _{i1}(t),\zeta _{i2}(t),\ldots,\zeta _{ig}(t)]\) are some measurable variables of the ith subsystem; (A
il
,B
il
,C
il
,D
il
,L
il
) denotes the lth local model for the ith subsystem; \(\bar {A}_{ikl}\) is the interconnection matrix between the ith and kth subsystems.
are fuzzy sets; \(x_{i}(t)\in \Re ^{n_{xi}},y_{i}(t)\in \Re ^{n_{yi}}\), and \(z_{i}(t)\in \Re ^{n_{zi}}\) are the system state, the measured output, and the estimated signal, respectively; \(w_{i}(t)\in \Re ^{n_{wi}}\) is the disturbance input, which belongs to \(l_{2}[0,\infty);\zeta _{i}(t):=[\zeta _{i1}(t),\zeta _{i2}(t),\ldots,\zeta _{ig}(t)]\) are some measurable variables of the ith subsystem; (A
il
,B
il
,C
il
,D
il
,L
il
) denotes the lth local model for the ith subsystem; \(\bar {A}_{ikl}\) is the interconnection matrix between the ith and kth subsystems.
Let us define \(\mu _{il}\left [ \zeta _{i}(t)\right ]\) as the normalized membership function of the inferred fuzzy set  ; it yields
; it yields
where \(\mu _{\textit {il}\phi }\left [ \zeta _{\textit {i}\phi }(t)\right ] \) denotes the grade of membership of ζ
i
ϕ
(t) in  . For convenience, in the sequel, the argument of \(\mu _{il}\left [ \zeta _{i}(t)\right ] \) will be dropped for the situations without ambiguity, i.e., we denote \(\mu _{il}:=\mu _{il}\left [ \zeta _{i}(t)\right ].\)
. For convenience, in the sequel, the argument of \(\mu _{il}\left [ \zeta _{i}(t)\right ] \) will be dropped for the situations without ambiguity, i.e., we denote \(\mu _{il}:=\mu _{il}\left [ \zeta _{i}(t)\right ].\)
By using a standard fuzzy inference, we obtain the ith global T-S fuzzy subsystem as below:
where
In this paper, we will address the distributed  filtering design problem of the discrete-time large-scale fuzzy system in (3) based on a piecewise Lyapunov functional (PLF). For each nonlinear subsystem \(i\in \mathcal {N}\), we follow the idea proposed in [36, 37], where the premise variable space is partitioned into two different kinds of regions: fuzzy regions and crisp regions. The region with \(0<\mu _{il}\left [\zeta _{i}(t)\right ] <1\) is defined as the fuzzy region, where the system dynamics are governed by a convex combination of several local models dropped into that region. In addition, the crisp region is the region where \(\mu _{il}\left [ \zeta _{i}(t)\right ] =1\) for some rules l, and the rest of membership functions equal to zero. The system dynamics in crisp region are governed by the l-th local model within that region.
filtering design problem of the discrete-time large-scale fuzzy system in (3) based on a piecewise Lyapunov functional (PLF). For each nonlinear subsystem \(i\in \mathcal {N}\), we follow the idea proposed in [36, 37], where the premise variable space is partitioned into two different kinds of regions: fuzzy regions and crisp regions. The region with \(0<\mu _{il}\left [\zeta _{i}(t)\right ] <1\) is defined as the fuzzy region, where the system dynamics are governed by a convex combination of several local models dropped into that region. In addition, the crisp region is the region where \(\mu _{il}\left [ \zeta _{i}(t)\right ] =1\) for some rules l, and the rest of membership functions equal to zero. The system dynamics in crisp region are governed by the l-th local model within that region.
Let  be the premise variable space partition for the ith subsystem, and
be the premise variable space partition for the ith subsystem, and  be the set of region indices. Based on the partition policy, the global T-S fuzzy system in (3) can be rewritten as
be the set of region indices. Based on the partition policy, the global T-S fuzzy system in (3) can be rewritten as

where
with \(0<\mu _{im}\left [ \zeta _{i}(t)\right ] <1,\sum _{m\in \mathcal {I}_{i}\left (j\right) }\mu _{im}\left [ \zeta _{i}(t)\right ] =1.\) For each local region \(\mathcal {S}_{ij},\mathcal {I}_{i}\left (j\right) \) contains the matrix indices used in that region. For a crisp region, \(\mathcal {I}_{i}\left (j\right) \) contains a single index.
For convenience, we denote a new set Ω i , which represents all possible region transitions for the ith subsystem:

where j≠s when ζ i (t) transits from the region \(\mathcal {S}_{ij}\) to \(\mathcal {S}_{is},\) and j=s when ζ i (t) stays in the same region \(\mathcal {S}_{ij}.\)
Given the large-scale fuzzy system (5) with the premise variable space partition, we propose a distributed piecewise filter of the following form:

where \(x_{Fi}(t)\in \Re ^{n_{fi}}\) is the filter state, \(z_{Fi}(t)\in \Re ^{n_{zi}}\) is an estimation of z i (t),y Fi (t) is the measured output applied to filter, and (A Fij ,B Fij ,B Fikj , C Fij ) are filter gains to be designed, where n fi =n xi for the full-order filter, and 1≤n fi <n xi for the reduced-order one.
Here, we assume that the data loss happens in the communication links between the filter and physical plain, the measured output y i (t) is no longer equivalent to y Fi (t). The ith filtering subsystem with unreliable communication network is shown in Fig. 1, where the ith filter takes all measured outputs via unreliable communication links. This paper models the data-loss condition based on a stochastic approach, thus, it yields [38]:
where \(\alpha _{i}\left (t\right) \) is the independent Bernoulli processes, which represent the unreliable condition of the links from the sensor to the filter. Specifically, \(\alpha _{i}\left (t\right) \equiv 0\) when the link fails, i.e., data are lost, and \(\alpha _{i}\left (t\right) \equiv 1\) represents successful transmission, and \(\alpha _{i}\left (t\right) \) is supposed to be given by
In addition, let us define
It is easy to see from (11) that
By defining \(\bar {x}_{i}(t)=\left [{x_{i}^{T}}(t) \; x_{Fi}^{T}(t)\right ]^{T},\bar {z}_{i}(t)=z_{i}(t)-z_{Fi}(t),\) and based on the large-scale fuzzy system in (5) and distributed piecewise filter in (8), the filtering error system is given by

where

Definition 1.
Let \(\tilde {x}\left (t\right) =\left [\bar {x}_{1}^{T}\left (t\right) \; \bar {x}_{2}^{T}\left (t\right) \; \cdots \;\bar {x}_{N}^{T}\left (t\right)\right ]^{T}\) and \(\tilde {w}\left (t\right) =\left [{w_{1}^{T}}\left (t\right) \; {w_{2}^{T}}\left (t\right) \; \cdots \; w_{N}^{T}\left (t\right)\right ]^{T}.\) Then, the filtering error system in (13) is stochastically stable in the mean square if there exists matrix W>0 such that
for any initial condition \(\tilde {x}\left (0\right) \) when \(\tilde {w}\left (t\right) \equiv 0.\)
Now, we formulate the distributed piecewise  filtering problem as below.
filtering problem as below.
Given the fuzzy filtering system shown in Fig. 1, assume that the communication link parameter \(\bar {\alpha }_{i}\) is available. Given a prescribed scalar γ>0, design a distributed piecewise filter in the form of (8) such that the following two conditions are satisfied simultaneously.
-
■■■
1) The filtering error system in (13) is stochastically stable in the sense of Definition 1;
-
■■■
2) Under zero-initial conditions, the estimated error \(\tilde {z}\left (t\right) \) satisfies
$$ \left\Vert \tilde{z}\right\Vert_{\mathbb{E}}\leq\gamma\left\Vert \tilde {w}\right\Vert_{2}, $$((16))where \(\left \Vert \tilde {z}\right \Vert _{\mathbb {E}}:=\mathbb {E}\left \{ \sqrt {\sum \limits _{t=0}^{\infty }\left \vert \tilde {z}\left (t\right) \right \vert ^{2}}\right \}.\)
If both the conditions are satisfied, then the filtering error system in (13) is stochastically stable with an  performance γ.
performance γ.
3 Main results
In this section, based on a piecewise Lyapunov functional (PLF), the performance analysis and design of the distributed piecewise  filter will be developed for the considered system in (3). The filter gains will be given for both full-order and reduced-order filters by solving a number of LMIs.
filter will be developed for the considered system in (3). The filter gains will be given for both full-order and reduced-order filters by solving a number of LMIs.
3.1 3.1 Distributed 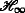 filtering performance analysis
filtering performance analysis
Here, we will present a distributed  filtering performance analysis, and the result can be summarized in the following lemma.
filtering performance analysis, and the result can be summarized in the following lemma.
Lemma 1.
Given the fuzzy system in (3) and distributed piecewise filter in (8), then the filtering error system in (13) is stochastically stable with an  performance γ, if there exist matrices
performance γ, if there exist matrices  and matrix multiplier \(\mathcal {G}_{i}\in \Re ^{\left (2n_{xi}+2n_{fi} +n_{wi}\right) \times (n_{xi}+n_{fi})}\), \(i\in \mathcal {N}\), and matrices
and matrix multiplier \(\mathcal {G}_{i}\in \Re ^{\left (2n_{xi}+2n_{fi} +n_{wi}\right) \times (n_{xi}+n_{fi})}\), \(i\in \mathcal {N}\), and matrices  , such that for all
, such that for all  , the following matrix inequalities hold:
, the following matrix inequalities hold:
where

Proof.
Choose the following piecewise Lyapunov functional (PLF):

where  , are positive definite symmetric Lyapunov matrices.
, are positive definite symmetric Lyapunov matrices.
Define Δ V i (t)=V i (t+1)−V i (t), one has
It follows from the error system in (13) that
where  .
.
Note that
where \(\bar {x},\bar {y}\in \Re ^{n}\) and matrix M=M T>0.
Define the matrix multipliers \(\mathcal {G}_{i}\in \Re ^{\left (2n_{xi} +2n_{fi}+n_{wi}\right)}\times (n_{xi}+n_{fi}),~i\in \mathcal {N}\), and the matrices \(0<H_{ikj}<H_{ik0}\in \Re ^{n_{xi} \times n_{xi} },\) and it follows from (21), (22) and Lemma A1 in the “Appendix” section that
Similarly, by introducing \(0<M_{ikj}<M_{ik0}\in \Re ^{n_{wi}\times n_{wi}},\) it yields
Given the following index
It follows from (19)–(21) and (23)–(25) that
where \(f_{i}=\sqrt {\bar {\alpha }_{i}\left (1-\bar {\alpha }_{i}\right) },\left \{ \Theta _{ijs},\Pi _{ij},\Psi _{ikj\left (1\right) },\Psi _{ikj\left (2\right) },\Psi _{ikj\left (3\right) },\right.\\\left.\Psi _{ikj\left (4\right) }\right \} \) are given by (18).
By using Schur complement lemma on (17), it is easy to see from (26) that the inequality (17) implies \(\mathbb {E}\left \{ \Delta V(t)\right \} <0\) when \(w_{i}\left (t\right) \equiv 0\). Thus, it yields

and

According to Definition 1, it is easy to see that the filtering error system is stochastically stable in the mean square. Then, considering \(\mathbb {E} \left \{ V\left (t\right) \right \} >0\) for all t≥0, under zero-initial conditions it yields
which means \(\left \Vert \tilde {z}\right \Vert _{\mathbb {E}}<\gamma \left \Vert \tilde {w}\right \Vert _{2}\), thus completing this proof.
3.2 3.2 Distributed 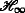 filtering design
filtering design
In this subsection, we will consider the distributed  filtering design for the system in (5). Based on Lemma 1, and by specifying the multiplier \(\mathcal {G}_{i}\), the nonlinear matrix inequalities are formulated into the linear ones, the corresponding result is summarized as below.
filtering design for the system in (5). Based on Lemma 1, and by specifying the multiplier \(\mathcal {G}_{i}\), the nonlinear matrix inequalities are formulated into the linear ones, the corresponding result is summarized as below.
Theorem 1.
Given the fuzzy system in (3) and a distributed filter in (8), the filtering error system in (13) is stochastically stable with an  performance γ, if there exist matrices
performance γ, if there exist matrices  , and matrices \(\bar {A}_{Fij}\in \Re ^{n_{fi}\times n_{fi}}\), \(\left \{ \bar {B}_{Fij},\bar {B}_{Fij}\right \} \in \Re ^{n_{fi}\times n_{yi}}\),
, and matrices \(\bar {A}_{Fij}\in \Re ^{n_{fi}\times n_{fi}}\), \(\left \{ \bar {B}_{Fij},\bar {B}_{Fij}\right \} \in \Re ^{n_{fi}\times n_{yi}}\),  , and matrices
, and matrices  , such that for all
, such that for all  the following LMIs hold:
the following LMIs hold:
where
Furthermore, a distributed piecewise filter in the form of (8) is given by

Proof.
For matrix inequality linearization purpose, the multipliers \(\mathcal {G}_{i},i\in \mathcal {N}\) are firstly specified by

where \(K=\left [\mathbf {I}_{n_{fi}} \; 0_{n_{fi}\times (n_{xi}-n_{fi})}\right ]^{T},G_{ij(1)}\in \Re ^{n_{xi}\times n_{xi}},G_{ij(2)}\in \Re ^{n_{fi}\times n_{fi}},G_{ij(3)}\in \Re ^{n_{fi}\times n_{xi}},G_{ij(4)}\in \Re ^{n_{fi}\times n_{fi}}.\)
Then, similar to [39], defining \(\Gamma := \text {diag}\left \{\mathbf {I} _{n_{xi}},G_{ij(2)}G_{ij(4)}^{-1}\right \}\), and performing a congruence transformation to

by Γ, it yields
Without loss of generalit, we can specify G i j(4)=G i j(2). Thus, we can directly specify the multipliers \(\mathcal {G}_{i}\) as

It is easy to see that the matrix variable  is absorbed by the filter gain variables
is absorbed by the filter gain variables  when introducing
when introducing
with  .
.
It is noted that the first block-row of \(\left \{ \mathbb {A}_{ij},\mathbb {\bar {A}}_{ikj},\mathbb {B}_{ij},\mathbb {\bar {B}}_{ikj}\right \} \) does not involve in the filter gain variables. Thus, the multipliers \(\mathcal {G} _{i},i\in \mathcal {N}\) is finally specified as below,

where \(G_{ij(5)}\in \Re ^{\left (n_{xi}+n_{fi}+n_{wi}\right) \times n_{xi}}.\)
Then, substituting (38) into (17), and by extracting the fuzzy basis functions, the inequality (30) can be obtained.
In addition, the inequality in (17) imply that
with  .
.
Due to the fact that P is >0, we have \(G_{ij(2)}+G_{ij(2)}^{T}>0,\) which means that the matrix variable G i j(2) are nonsingular. Thus, the filtering gains \(\left \{ A_{Fij},B_{Fij},B_{Fikj},C_{Fij}\right \} \) can be obtained by (32) and completing this proof.
4 Simulation examples
In the following, let us consider two examples to illustrate the result proposed in this paper.
Example 1.
Consider a discrete-time large-scale T-S model with three fuzzy rules as below:
Plant rule
 : IF
x
i1(t) is
: IF
x
i1(t) is  , THEN
, THEN
where
for the first subsystem, and
for the second subsystem.
Figure 2 shows the membership functions. According to the premise variable space partition, there are three subspaces for each subsystem:
It can be observed that \(\mathcal {S}_{i1}\) is a crisp region; both \(\mathcal {S}_{i2}\) and \(\mathcal {S}_{i3}\) are fuzzy regions. The region index set is  .
.
Here, we consider the case of a full-order filter with a
i
=0.6. It is noted that the common Lyapunov function proposed in [40] is not applicable to the distributed  filtering design for this case in this example. However, by applying Theorem 1, the feasible solutions of \(\gamma _{\min }=3.9555\) for the full-order filter and \(\gamma _{\min }=6.5599\) for the reduced-order filter are obtained, and the corresponding filter gains are
filtering design for this case in this example. However, by applying Theorem 1, the feasible solutions of \(\gamma _{\min }=3.9555\) for the full-order filter and \(\gamma _{\min }=6.5599\) for the reduced-order filter are obtained, and the corresponding filter gains are

for full-order filter and
for the reduced-order case.
Example 2.
Consider a modified double-inverted pendulum, which is connected by a spring [34]. The motional equations of the interconnected pendulum are given by
where x i1 and x i2 denote the angle from the vertical and the angular velocity, respectively.
In this simulation, the moments of inertia are J 1=2 kg and J 2=2.5 kg; the masses of two pendulums are chosen as m 1=2 kg and m 2=2.5 kg; the constant of the connecting torsional spring is k=8 N ·m/rad; the length of the pendulum is r=1 m; the gravity constant is g=9.8 m/s2. Here, the interconnected pendulum is linearized around the origin, \(x_{i1}=\left (\pm 80^{\circ},0\right) \) and \(x_{i1}=\left (\pm 88^{\circ},0\right) \); each pendulum is described by the T-S model with three fuzzy rules. Given u 1=−18x 11−16x 12 and u 2=−20x 21−14x 22, it can be known that these two closed-loop T-S fuzzy subsystems are stable. Then, by discretizing the T-S fuzzy systems with sampling period T=0.01 s, the discrete-time interconnected T-S fuzzy system can be obtained as below:
Plant rule
 : IF
\(\left \vert x_{i1}(t)\right \vert \) is
: IF
\(\left \vert x_{i1}(t)\right \vert \) is  , THEN
, THEN
where
for the first subsystem and
for the second subsystem.
Figure 3 shows the membership functions. Based on the premise variable space partition, it can be known that there exist three subspaces for each subsystem:
where r
i1=0,r
i2=8°,r
i3=80°, and r
i4=88°. It is shown that both \(\mathcal {S}_{i1}\) and \(\mathcal {S}_{i3}\) are crisp regions and \(\mathcal {S}_{i2}\) is a fuzzy region. The region index set is  .
.
Now, considering the case of full-order filter with a
i
=0.9, the common Lyapunov function proposed in [40] is not applicable to the distributed  filtering design for this case in this example. However, by applying Theorem 1, the
filtering design for this case in this example. However, by applying Theorem 1, the  filtering performance \(\gamma _{\min }=3.3755\) is obtained, and the obtained filter gains are
filtering performance \(\gamma _{\min }=3.3755\) is obtained, and the obtained filter gains are
and
Given the initial conditions x
1(0)=[1.3,0]T,x
2(0)=[1.1,0]T, and assume that the external disturbances satisfy \(w_{1}(t)=5\textit {e}^{-0.02t}\sin (t)\) and \(w_{2}(t)=5\textit {e}^{-0.02t}\cos (t),\) it is easy to see from Figs. 4 and 5 that the responses of he time responses of z
i
(t) and \({z}_{Fi}(t),i=\left \{ 1,2\right \} \) converge to zero. The data-packet dropouts are shown in Figs. 6 and 7, respectively. Then, it can also be shown in Fig. 8 that the  performance is satisfactory under zero-initial conditions thus verifying the effectiveness of the distributed
performance is satisfactory under zero-initial conditions thus verifying the effectiveness of the distributed  filtering design.
filtering design.
5 Conclusions
This paper has investigated the distributed  filtering design for discrete-time large-scale T-S fuzzy systems, which exchange their information through unreliable communication network. Based on a piecewise Lyapunov function and some convexifying techniques, less conservative results on the distributed piecewise
filtering design for discrete-time large-scale T-S fuzzy systems, which exchange their information through unreliable communication network. Based on a piecewise Lyapunov function and some convexifying techniques, less conservative results on the distributed piecewise  filtering design were derived for the considered system in terms of LMIs. The effectiveness of the method proposed in this paper was validated by using two examples.
filtering design were derived for the considered system in terms of LMIs. The effectiveness of the method proposed in this paper was validated by using two examples.
6 Appendix
Lemma A1.
[ 41 ] Given matrix \(0<W=W^{T}\in \Re ^{n\times n},\) two positive integers d 2 and d 1 satisfy d 2≥d 1≥1. Then, it yields
where \(\bar {d}=d_{2}-d_{1}+1.\)
References
D Siljak, Large-Scale Dynamic Systems: Stability and Structure (Elsevier/North-Holland, New York, 1978).
D Penkin, G Janssen, A Yarovoy, Source positioning in a large-scale tiny-sensor network of arbitrary topology. EURASIP J. Adv. Sig. Process. 57:, 1–11 (2014).
Z Hu, C Feng, T Zhang, Q Niu, Y Chen, Nonlinear joint transmit-receive processing for coordinated multi-cell systems: centralized and decentralized. EURASIP J. Adv. Sig. Process. 10:, 1–14 (2015).
L Bakule, Decentralized control: status and outlook. Annu. Rev. Control. 38(1), 71–80 (2014).
F Kazempour, J Ghaisari, Stability analysis of model-based networked distributed control systems. J. Process Control. 23(3), 444–452 (2013).
I Guerreiro, D Hui, C Cavalcante, A distributed approach to precoder selection using factor graphs for wireless communication networks. EURASIP J. Adv. Sig. Process. 83:, 1–18 (2013).
H Maa, H Cakmak, F Bach, R Mikut, et al., Data processing of high-rate low-voltage distribution grid recordings for smart grid monitoring and analysis. EURASIP J. Adv. Sig. Process. 14:, 1–21 (2015).
T Tanaka, HO Wang, Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach (Wiley, New York, 2001).
J Qiu, H Tian, Q Lu, H Gao, Nonsynchronized robust filtering design for continuous-time T-S fuzzy affine dynamic systems based on piecewise Lyapunov functions. IEEE Trans. Cybern. 43(6), 1755–1766 (2013).
L Li, SX Ding, J Qiu, Y Yang, Y Zhang, Weighted fuzzy observer-based fault detection approach for discrete-time nonlinear systems via piecewise-fuzzy Lyapunov functions. IEEE Trans. Fuzzy Syst. doi:10.1109/TFUZZ.2016.2514371.
L Li, SX Ding, J Qiu, Y Yang, Real-time fault detection approach for nonlinear systems and its asynchronous T-S fuzzy observer-based implementation. IEEE Trans. Cybern. doi:10.1109/TCYB.2015.2513438.
M Wang, J Qiu, M Chadli, M Wang, A switched system approach to exponential stabilization of sampled-data T-S fuzzy systems with packet dropouts. IEEE Trans. Cybern. doi:10.1109/TCYB.2015.2498522.
J Qiu, SX Ding, H Gao, S Yin, Fuzzy-model-based reliable static output feedback
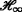 control of nonlinear hyperbolic PDE systems. IEEE Trans. Fuzzy Syst (2015). doi:10.1109/TFUZZ.2015.2457934.
control of nonlinear hyperbolic PDE systems. IEEE Trans. Fuzzy Syst (2015). doi:10.1109/TFUZZ.2015.2457934.G Feng, A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 14(5), 676–697 (2006).
J Qiu, H Gao, S Ding, Recent advances on fuzzy-model-based nonlinear networked control systems: a survey. IEEE Trans. Ind. Electron (2015). doi:10.1109/TIE.2015.2504351.
J Qiu, G Feng, H Gao, Nonsynchronized-state estimation of multichannel networked nonlinear systems with multiple packet dropouts via T-S fuzzy-affine dynamic models. IEEE Trans. Fuzzy Syst. 19(1), 75–90 (2011).
C Zhang, G Feng, J Qiu, W Zhang, T-S fuzzy-model-based piecewise
 output feedback controller design for networked nonlinear systems with medium access constraint. Fuzzy Sets Syst. 248(1), 86–105 (2014).
output feedback controller design for networked nonlinear systems with medium access constraint. Fuzzy Sets Syst. 248(1), 86–105 (2014).M Chadli, T Guerra, LMI solution for robust static output feedback control of discrete Takagi-Sugeno fuzzy models. IEEE Trans. Fuzzy Syst. 20(6), 1160–1165 (2012).
T Wang, H Gao, J Qiu, A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Trans. Neural Netw. Learn. Syst (2015). doi:10.1109/TNNLS.2015.2411671.
Y Shi, B Yu, Output feedback stabilization of networked control systems with random delays modeled by Markov chains. IEEE Trans. Autom. Control. 54(7), 1668–1674 (2009).
Y Zhu, L Zhang, W Zheng, Distributed
 filtering for a class of discrete-time Markov jump Lure systems with redundant channels. IEEE Trans. Ind. Electron (2015). doi:10.1109/TIE.2015.2499169.
filtering for a class of discrete-time Markov jump Lure systems with redundant channels. IEEE Trans. Ind. Electron (2015). doi:10.1109/TIE.2015.2499169.J Qiu, G Feng, H Gao, Observer-based piecewise affine output feedback controller synthesis of continuous-time T-S fuzzy affine dynamic systems using quantized measurements. IEEE Trans. Fuzzy Syst. 20(6), 1046–1062 (2012).
Y Wei, J Qiu, HR Karimi, M Wang, A new design of
 filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 93(9), 2392–2407 (2013).
filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 93(9), 2392–2407 (2013).C Zhang, G Feng, J Qiu, Y Shen, Control synthesis for a class of linear network-based systems with communication constraints. IEEE Trans. Ind. Electron. 60(8), 3339–3348 (2013).
C Zhang, G Feng, H Gao, J Qiu,
 filtering for nonlinear discrete-time systems subject to quantization and packet dropouts. Fuzzy Sets Syst. 19(2), 353–365 (2011).
filtering for nonlinear discrete-time systems subject to quantization and packet dropouts. Fuzzy Sets Syst. 19(2), 353–365 (2011).J Qiu, Y Wei, HR Karimi, New approach to delay-dependent
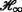 control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions. J. Frankl. Inst. 352(1), 189–215 (2015).
control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions. J. Frankl. Inst. 352(1), 189–215 (2015).Y Zhu, Q Zhang, Z Wei, L Zhang, Robust stability analysis of Markov jump standard genetic regulatory networks with mixed time delays and uncertainties. Neurocomputing. 110(13), 44–50 (2013).
Y Shi, T Chen, Optimal design of multichannel transmultiplexers with stopband energy and passband magnitude constraints. IEEE Trans. Circ. Syst. II Analog Digit. Signal Process. 50(9), 659–662 (2003).
Y Wei, J Qiu, HR Karimi, M Wang, New approach to delay-dependent
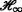 filtering for discrete-time Markovian jump systems with time-varying delay and incomplete transition descriptions. Iet Control. Theory Appl. 7(5), 684–696 (2013).
filtering for discrete-time Markovian jump systems with time-varying delay and incomplete transition descriptions. Iet Control. Theory Appl. 7(5), 684–696 (2013).F Hsiao, JH Wang, C Chen, Z Tsai, Robust stabilization of nonlinear multiple time-delay large-scale systems via decentralized fuzzy control. IEEE Trans. Fuzzy Syst. 13(1), 152–163 (2005).
C Hua, S Ding, Decentralized networked control system design using T-S fuzzy approach. IEEE Trans. Fuzzy Syst. 20(1), 9–21 (2012).
Z Zhong, J Yu, Y He, T Hayat, F Alsaadi, Fuzzy-model-based decentralized dynamic-output-feedback
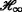 control for large-scale nonlinear systems with time-varying delays. Neurocomputing (2015). doi:10.1016/j.neucom.2015.08.062.
control for large-scale nonlinear systems with time-varying delays. Neurocomputing (2015). doi:10.1016/j.neucom.2015.08.062.Z Zhong, S Fu, T Hayat, F Alsaadi, G Sun, Decentralized piecewise
 fuzzy filtering design for discrete-time large-scale nonlinear systems with time-varying delay. J. Frankl. Inst. 352(9), 3782–3807 (2015).
fuzzy filtering design for discrete-time large-scale nonlinear systems with time-varying delay. J. Frankl. Inst. 352(9), 3782–3807 (2015).H Zhang, H Zhong, C Dang, Delay-dependent decentralized filtering for discrete-time nonlinear interconnected systems with time-varying delay based on the T-S fuzzy model. IEEE Trans. Fuzzy Syst. 20(3), 431–443 (2012).
Z Zhong, S Fu, T Hayat, F Alsaadi, G Sun, New results on decentralized
 fuzzy filtering design for continuous-time large-scale nonlinear systems with time-varying delay. Circ. Syst. Signal Process. 35(2), 527–552 (2016).
fuzzy filtering design for continuous-time large-scale nonlinear systems with time-varying delay. Circ. Syst. Signal Process. 35(2), 527–552 (2016).M Johansson, A Rantzer, K-E Å rzén, Piecewise quadratic stability of fuzzy systems. IEEE Trans. Fuzzy Syst. 7(6), 713–722 (1999).
J Qiu, G Feng, H Gao, Static output feedback
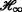 control of continuous-time T-S fuzzy affine systems via piecewise Lyapunov functions. IEEE Trans. Fuzzy Syst. 21(2), 245–261 (2013).
control of continuous-time T-S fuzzy affine systems via piecewise Lyapunov functions. IEEE Trans. Fuzzy Syst. 21(2), 245–261 (2013).J Qiu, G Feng, H Gao, Fuzzy-model-based piecewise
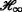 static-output-feedback controller design for networked nonlinear systems. IEEE Trans. Fuzzy Syst. 18(5), 919–934 (2010).
static-output-feedback controller design for networked nonlinear systems. IEEE Trans. Fuzzy Syst. 18(5), 919–934 (2010).J Qiu, G Feng, J Yang, A new design of delay-dependent robust
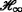 filtering for discrete-time T-S fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 17(5), 1044–1058 (2009).
filtering for discrete-time T-S fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 17(5), 1044–1058 (2009).H Zhang, S Liu, D Liu, Fuzzy
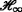 filter design for a class of nonlinear discrete-time systems with multiple time delays. IEEE Trans. Fuzzy Syst. 15(3), 453–469 (2007).
filter design for a class of nonlinear discrete-time systems with multiple time delays. IEEE Trans. Fuzzy Syst. 15(3), 453–469 (2007).X Jiang, Q Han, X Yu, in Proceedings of the 2005 IEEE Conference on American Control, 4. Stability criteria for linear discrete-time systems with interval-like time-varying delay, (2005), pp. 2817–2822, doi:10.1109/ACC.2005.1470396.
Acknowledgements
The authors wish to thank the Editor-in-Chief, Associate Editor, and anonymous reviewers for their helpful comments which have improved the paper.
The work was supported in part by the Natural Science Foundation of Fujian Province(2016J01267), and by the Fujian Provincial Major Scientific and Technological Projects (2014H6028), and by the Scientific Research Items of XMUT (XYK201401), and by the Advanced Research Project of XUMT (YKJ12010R).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shao, Z., Chen, T. Distributed piecewise 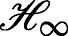 filtering design for large-scale networked nonlinear systems.
EURASIP J. Adv. Signal Process. 2016, 51 (2016). https://doi.org/10.1186/s13634-016-0350-2
filtering design for large-scale networked nonlinear systems.
EURASIP J. Adv. Signal Process. 2016, 51 (2016). https://doi.org/10.1186/s13634-016-0350-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-016-0350-2

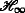 filtering performance analysis
filtering performance analysis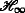 filtering design
filtering design






 performance
performance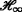 control of nonlinear hyperbolic PDE systems. IEEE Trans. Fuzzy Syst (2015). doi:
control of nonlinear hyperbolic PDE systems. IEEE Trans. Fuzzy Syst (2015). doi: output feedback controller design for networked nonlinear systems with medium access constraint. Fuzzy Sets Syst. 248(1), 86–105 (2014).
output feedback controller design for networked nonlinear systems with medium access constraint. Fuzzy Sets Syst. 248(1), 86–105 (2014). filtering for a class of discrete-time Markov jump Lure systems with redundant channels. IEEE Trans. Ind. Electron (2015). doi:
filtering for a class of discrete-time Markov jump Lure systems with redundant channels. IEEE Trans. Ind. Electron (2015). doi: filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 93(9), 2392–2407 (2013).
filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 93(9), 2392–2407 (2013). filtering for nonlinear discrete-time systems subject to quantization and packet dropouts. Fuzzy Sets Syst. 19(2), 353–365 (2011).
filtering for nonlinear discrete-time systems subject to quantization and packet dropouts. Fuzzy Sets Syst. 19(2), 353–365 (2011). control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions. J. Frankl. Inst. 352(1), 189–215 (2015).
control for continuous-time Markovian jump systems with time-varying delay and deficient transition descriptions. J. Frankl. Inst. 352(1), 189–215 (2015). filtering for discrete-time Markovian jump systems with time-varying delay and incomplete transition descriptions. Iet Control. Theory Appl. 7(5), 684–696 (2013).
filtering for discrete-time Markovian jump systems with time-varying delay and incomplete transition descriptions. Iet Control. Theory Appl. 7(5), 684–696 (2013). control for large-scale nonlinear systems with time-varying delays. Neurocomputing (2015). doi:
control for large-scale nonlinear systems with time-varying delays. Neurocomputing (2015). doi: fuzzy filtering design for discrete-time large-scale nonlinear systems with time-varying delay. J. Frankl. Inst. 352(9), 3782–3807 (2015).
fuzzy filtering design for discrete-time large-scale nonlinear systems with time-varying delay. J. Frankl. Inst. 352(9), 3782–3807 (2015). fuzzy filtering design for continuous-time large-scale nonlinear systems with time-varying delay. Circ. Syst. Signal Process. 35(2), 527–552 (2016).
fuzzy filtering design for continuous-time large-scale nonlinear systems with time-varying delay. Circ. Syst. Signal Process. 35(2), 527–552 (2016). control of continuous-time T-S fuzzy affine systems via piecewise Lyapunov functions. IEEE Trans. Fuzzy Syst. 21(2), 245–261 (2013).
control of continuous-time T-S fuzzy affine systems via piecewise Lyapunov functions. IEEE Trans. Fuzzy Syst. 21(2), 245–261 (2013). static-output-feedback controller design for networked nonlinear systems. IEEE Trans. Fuzzy Syst. 18(5), 919–934 (2010).
static-output-feedback controller design for networked nonlinear systems. IEEE Trans. Fuzzy Syst. 18(5), 919–934 (2010). filtering for discrete-time T-S fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 17(5), 1044–1058 (2009).
filtering for discrete-time T-S fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 17(5), 1044–1058 (2009). filter design for a class of nonlinear discrete-time systems with multiple time delays. IEEE Trans. Fuzzy Syst. 15(3), 453–469 (2007).
filter design for a class of nonlinear discrete-time systems with multiple time delays. IEEE Trans. Fuzzy Syst. 15(3), 453–469 (2007). filter
filter