- Research Article
- Open access
- Published:
Audio Signal Processing Using Time-Frequency Approaches: Coding, Classification, Fingerprinting, and Watermarking
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 451695 (2010)
Abstract
Audio signals are information rich nonstationary signals that play an important role in our day-to-day communication, perception of environment, and entertainment. Due to its non-stationary nature, time- or frequency-only approaches are inadequate in analyzing these signals. A joint time-frequency (TF) approach would be a better choice to efficiently process these signals. In this digital era, compression, intelligent indexing for content-based retrieval, classification, and protection of digital audio content are few of the areas that encapsulate a majority of the audio signal processing applications. In this paper, we present a comprehensive array of TF methodologies that successfully address applications in all of the above mentioned areas. A TF-based audio coding scheme with novel psychoacoustics model, music classification, audio classification of environmental sounds, audio fingerprinting, and audio watermarking will be presented to demonstrate the advantages of using time-frequency approaches in analyzing and extracting information from audio signals.
1. Introduction
A normal human can hear sound vibrations in the range of 20 Hz to 20 kHz. Signals that create such audible vibrations qualify as an audio signal. Creating, modulating, and interpreting audio clues were among the foremost abilities that differentiated humans from the rest of the animal species. Over the years, methodical creation and processing of audio signals resulted in the development of different forms of communication, entertainment, and even biomedical diagnostic tools. With the advancements in the technology, audio processing was automated and various enhancements were introduced. The current digital era furthered the audio processing with the power of computers. Complex audio processing tasks were easily implemented and performed in blistering speeds. The digitally converted and formatted audio signals brought in high levels of noise immunity with guaranteed quality of reproduction over time. However, the benefits of digital audio format came with the penalty of huge data rates and difficulties in protecting copyrighted audio content over Internet. On the other hand, the ability to use computers brought in great power and flexibility in analyzing and extracting information from audio signals. This contrasting pros and cons of digital audio inspired the development of variety of audio processing techniques.
In general, a majority of audio processing techniques address the following 3 application areas:  compression,
compression,  classification, and
classification, and  security. The underlying theme (or motivation) for each of these areas is different and at sometimes contrasting, which poses a major challenge to arrive at a single solution. In spite of the bandwidth expansion and better storage solution, compression still plays an important role particularly in mobile devices and content delivery over Internet. While the requirement of compaction (in terms of retaining major audio components) drives the audio coding approaches, audio classification requires the extraction of subtle, accurate, and discriminatory information to group or index a variety of audio signals. It also covers a wide range of subapplications where the accuracy of the extracted audio information plays a vital role in content-based retrievals, sensing auditory environment for critical applications, and biometrics. Unlike compaction in audio coding or extraction of information in classification, to protect the digital audio content addition of information in the form of a security key is required which would then prove the ownership of the audio content. The addition of the external message (or key) should be in such a way that the addition does not cause perceptual distortions and remains robust from attacks to remove it. Considering the above requirements it would be difficult to address all the above application areas with a universal methodology unless we could model the audio signal as accurately as possible in a joint TF plane and then adaptively process the model parameters depending upon the application. In line with the above 3 application areas, this paper presents and discusses a TF-based audio coding scheme, music classification, audio classification of environmental sounds, audio fingerprinting, and audio watermarking.
security. The underlying theme (or motivation) for each of these areas is different and at sometimes contrasting, which poses a major challenge to arrive at a single solution. In spite of the bandwidth expansion and better storage solution, compression still plays an important role particularly in mobile devices and content delivery over Internet. While the requirement of compaction (in terms of retaining major audio components) drives the audio coding approaches, audio classification requires the extraction of subtle, accurate, and discriminatory information to group or index a variety of audio signals. It also covers a wide range of subapplications where the accuracy of the extracted audio information plays a vital role in content-based retrievals, sensing auditory environment for critical applications, and biometrics. Unlike compaction in audio coding or extraction of information in classification, to protect the digital audio content addition of information in the form of a security key is required which would then prove the ownership of the audio content. The addition of the external message (or key) should be in such a way that the addition does not cause perceptual distortions and remains robust from attacks to remove it. Considering the above requirements it would be difficult to address all the above application areas with a universal methodology unless we could model the audio signal as accurately as possible in a joint TF plane and then adaptively process the model parameters depending upon the application. In line with the above 3 application areas, this paper presents and discusses a TF-based audio coding scheme, music classification, audio classification of environmental sounds, audio fingerprinting, and audio watermarking.
The paper is organized as follows. Section 2 is devoted to the theories and the algorithms related to TF analysis. Section 3 will deal with the use of TF analysis in audio coding and also will present the comparisons among some of the audio coding technologies including adaptive time-frequency transform (ATFT) coding, MPEG-Layer 3 (MP3) coding and MPEG Advanced Audio Coding (AAC). In Section 4, TF analysis-based music classification and environmental sounds classification will be covered. Section 5 will present fingerprinting and watermarking of audio signals using TF approaches and summary of the paper will be provided in Section 6.
2. Time-Frequency Analysis
Signals can be classified into different classes based on their characteristics. One such classification is deterministic and random signals. Deterministic signals are those, which can be represented mathematically or in other words all information about the signals are known a priori. Random signals take random values and cannot be expressed in a simple mathematical form like deterministic signals, instead they are represented using their probabilistic statistics. When the statistics of such signals vary over time, they qualify to form another subdivision called nonstationary signals. Nonstationary signals are associated with time-varying spectral content and most of the real world (including audio) signals fall into this category. Due to the time-varying behavior, it is challenging to analyze nonstationary signals.
Early signal processing techniques were mainly using time-domain operations such as correlation, convolution, inner product, and signal averaging. While the time-domain operations provided some information about the signal they were limited in their ability to extract the frequency content of a signal. Introduction of Fourier theory addressed this issue by enabling the analysis of signals in the frequency domain. However, Fourier technique provided only the global frequency content of a signal and not the time occurrences of those frequencies. Hence neither time-domain nor frequency domain analysis were sufficient enough to analyze signals with time-varying frequency content. To over come this difficulty and to analyze the nonstationary signals effectively, techniques which could give joint time and frequency information were needed. This gave birth to the TF transformations.
In general, TF transformations can be classified into two main categories based on  Signal decomposition approaches, and
Signal decomposition approaches, and  Bilinear TF distributions (also known as Cohen's class). In decomposition-based approach the signal is approximated into small TF functions derived from translating, modulating, and scaling a basis function having a definite time and frequency localization. Distributions are two dimensional energy representations with high TF resolution. Depending upon the application in hand and the feature extraction strategies either the TF decomposition approach or TF distribution approach could be used.
Bilinear TF distributions (also known as Cohen's class). In decomposition-based approach the signal is approximated into small TF functions derived from translating, modulating, and scaling a basis function having a definite time and frequency localization. Distributions are two dimensional energy representations with high TF resolution. Depending upon the application in hand and the feature extraction strategies either the TF decomposition approach or TF distribution approach could be used.
2.1. Adaptive Time-Frequency Transform (ATFT) Algorithm—Decomposition Approach
The ATFT technique is based on the matching pursuit algorithm with TF dictionaries [1, 2]. ATFT has excellent TF resolution properties (better than Wavelets and Wavelet Packets) and due to its adaptive nature (handling non-stationarity), there is no need for signal segmentations. Flexible signal representations can be achieved as accurately as possible depending upon the characteristics of the TF dictionary.
In the ATFT algorithm, any signal  is decomposed into a linear combination of TF functions
is decomposed into a linear combination of TF functions  selected from a redundant dictionary of TF functions [2]. In this context, redundant dictionary means that the dictionary is overcomplete and contains much more than the minimum required basis functions, that is, a collection of nonorthogonal basis functions, that is, much larger than the minimum required basis functions to span the given signal space. Using ATFT, we can model any given signal
selected from a redundant dictionary of TF functions [2]. In this context, redundant dictionary means that the dictionary is overcomplete and contains much more than the minimum required basis functions, that is, a collection of nonorthogonal basis functions, that is, much larger than the minimum required basis functions to span the given signal space. Using ATFT, we can model any given signal  as
as

where

and  are the expansion coefficients. The choice of the window function
are the expansion coefficients. The choice of the window function  determines the characteristics of the TF dictionary. The dictionary of TF functions can either suitably be modified or selected based on the application in hand. The scale factor
determines the characteristics of the TF dictionary. The dictionary of TF functions can either suitably be modified or selected based on the application in hand. The scale factor  , also called as octave parameter, is used to control the width of the window function, and the parameter
, also called as octave parameter, is used to control the width of the window function, and the parameter  controls the temporal placement. The parameters
controls the temporal placement. The parameters  and
and  are the frequency and phase of the exponential function, respectively. The index
are the frequency and phase of the exponential function, respectively. The index  represents a particular combination of the TF decomposition parameters (
represents a particular combination of the TF decomposition parameters ( ,
,  ,
,  and
and  ). In the TF decomposition-based works that will be presented at later part of this paper, a Gabor dictionary (Gaussian functions, i.e.,
). In the TF decomposition-based works that will be presented at later part of this paper, a Gabor dictionary (Gaussian functions, i.e.,  in (2)) was used which has the best TF localization properties [3] and in the discrete ATFT algorithm implementation used in these works, the octave parameter
in (2)) was used which has the best TF localization properties [3] and in the discrete ATFT algorithm implementation used in these works, the octave parameter  could take any equivalent time-width value between
could take any equivalent time-width value between  to
to  ; the phase parameter
; the phase parameter  could take any value between 0 to 1 scaled to 0 to 180 degrees; the frequency parameter
could take any value between 0 to 1 scaled to 0 to 180 degrees; the frequency parameter  could take one of the 8192 levels corresponding to 0 to 22,050 Hz (i.e., sampling frequency of 44,100 Hz for wideband audio); the temporal position parameter
could take one of the 8192 levels corresponding to 0 to 22,050 Hz (i.e., sampling frequency of 44,100 Hz for wideband audio); the temporal position parameter  could take any value between 1 to the length of the signal.
could take any value between 1 to the length of the signal.
The signal  is projected over a redundant dictionary of TF functions with all possible combinations of scaling, translations, and modulations. When
is projected over a redundant dictionary of TF functions with all possible combinations of scaling, translations, and modulations. When  is real and discrete, like the audio signals in the presented technique, we use a dictionary of real and discrete TF functions. Due to the redundant or overcomplete nature of the dictionary it gives extreme flexibility to choose the best fit for the local signal structures (local optimization) [2]. This extreme flexibility enables to model a signal as accurately as possible with the minimum number of TF functions providing a compact approximation of the signal. At each iteration, the best matched TF function (i.e., the TF function that captured maximum fraction of signal energy) was searched and selected from the Gabor dictionary. The best match depends on the choice function and in this work maximum energy capture per iteration was used as described in [1]. The remaining signal called the residue was further decomposed in the same way at each iteration subdividing them into TF functions. Due to the sequential selection of the TF functions, the signal decomposition may take longer times especially for longer signals. To overcome this, there exists faster approaches in choosing multiple TF functions in each of the iterations [4]. After
is real and discrete, like the audio signals in the presented technique, we use a dictionary of real and discrete TF functions. Due to the redundant or overcomplete nature of the dictionary it gives extreme flexibility to choose the best fit for the local signal structures (local optimization) [2]. This extreme flexibility enables to model a signal as accurately as possible with the minimum number of TF functions providing a compact approximation of the signal. At each iteration, the best matched TF function (i.e., the TF function that captured maximum fraction of signal energy) was searched and selected from the Gabor dictionary. The best match depends on the choice function and in this work maximum energy capture per iteration was used as described in [1]. The remaining signal called the residue was further decomposed in the same way at each iteration subdividing them into TF functions. Due to the sequential selection of the TF functions, the signal decomposition may take longer times especially for longer signals. To overcome this, there exists faster approaches in choosing multiple TF functions in each of the iterations [4]. After  iterations, signal
iterations, signal  could be expressed as
could be expressed as

where the first part of (3) is the decomposed TF functions until  iterations, and the second part is the residue which will be decomposed in the subsequent iterations. This process is repeated till all the energy of the signal is decomposed. At each iteration some portion of the signal energy was modeled with an optimal TF resolution in the TF plane. Over iterations it can be observed the captured energy increases and the residue energy falls. Based on the signal content the value of
iterations, and the second part is the residue which will be decomposed in the subsequent iterations. This process is repeated till all the energy of the signal is decomposed. At each iteration some portion of the signal energy was modeled with an optimal TF resolution in the TF plane. Over iterations it can be observed the captured energy increases and the residue energy falls. Based on the signal content the value of  could be very high for a complete decomposition (i.e.,
could be very high for a complete decomposition (i.e.,  ). Examples of Gaussian TF functions with different scales and modulation parameters are shown in Figure 1. The order of computational complexity for one iteration of the ATFT algorithm is given by
). Examples of Gaussian TF functions with different scales and modulation parameters are shown in Figure 1. The order of computational complexity for one iteration of the ATFT algorithm is given by  where
where  is the length of the signal samples. The time complexity of the ATFT algorithm increases with the increase in the number of iterations required to model a signal, which in turn depends on the nature of the signal. Compared to this the computational complexity of Modified Discrete Cosine Transform (MDCT) used in few of the state-of-the-art audio coders is only
is the length of the signal samples. The time complexity of the ATFT algorithm increases with the increase in the number of iterations required to model a signal, which in turn depends on the nature of the signal. Compared to this the computational complexity of Modified Discrete Cosine Transform (MDCT) used in few of the state-of-the-art audio coders is only  (same as FFT).
(same as FFT).
Once the signal is modeled accurately or decomposed into TF functions with definite time and frequency localization, the TF parameters governing the TF functions could be analyzed for extracting application-specific information. In our case we process the TF decomposition parameters of the audio signals to perform both audio compression and classification as will be explained in the later sections.
2.2. TF Distribution Approach
TF distribution (TFD) indicates a two-dimensional energy representations of a signal in terms of time-and frequency-domains. The work in the area of TFD methods is extensive [2, 5–7]. Some well-known TFD techniques are as follows.
2.2.1. Linear TFDs
The simplest linear TFD is the squared modulus of STFT of a signal, which assumes that the signal is stationary in short durations and multiplies the signal by a window, and takes the Fourier transform on the windowed segments. This joint TF representation represents the localization of frequency in time; however, it suffers from TF resolution tradeoff.
2.2.2. Quadratic TFDs
In quadratic TFDs, the analysis window is adapted to the analyzed signal. To achieve this, the quadratic TFD transforms the time varying autocorrelation of the signal to obtain a representation of the signal energy distributed over time and frequency

where  is Wigner-Ville distribution (WVD) of the signal. WVD offers higher resolution than STFT; however, when more than one component exists in the signal, the WVD contains interference cross terms. Interference cross terms do not belong to the signal and are generated by the quadratic nature of the WVD. They generate highly oscillatory interference in the TFD, and their presence will lead to incorrect interpretation of the signal properties. This drawback of the WVD is the motivation for introducing other TFDs such as Pseudo Wigner-Ville Distribution (PWVD), SPWVD, Choi-Williams Distribution (CWD), and Cohen kernel distribution to define a kernel in ambiguity domain that can eliminate cross terms. These distributions belong to a general class called the Cohens class of bilinear TF representation [3]. These TFDs are not always positive. In order to produce meaningful features, the value of the TFD should be positive at each point; otherwise the extracted features may not be interpretable, for example, the WVD always results in positive instantaneous frequency, but it also gives that the expectation value of the square of the frequency, for a fixed time, can become negative which does not make any sense [8]. Additionally, it is very difficult to explain negative probabilities.
is Wigner-Ville distribution (WVD) of the signal. WVD offers higher resolution than STFT; however, when more than one component exists in the signal, the WVD contains interference cross terms. Interference cross terms do not belong to the signal and are generated by the quadratic nature of the WVD. They generate highly oscillatory interference in the TFD, and their presence will lead to incorrect interpretation of the signal properties. This drawback of the WVD is the motivation for introducing other TFDs such as Pseudo Wigner-Ville Distribution (PWVD), SPWVD, Choi-Williams Distribution (CWD), and Cohen kernel distribution to define a kernel in ambiguity domain that can eliminate cross terms. These distributions belong to a general class called the Cohens class of bilinear TF representation [3]. These TFDs are not always positive. In order to produce meaningful features, the value of the TFD should be positive at each point; otherwise the extracted features may not be interpretable, for example, the WVD always results in positive instantaneous frequency, but it also gives that the expectation value of the square of the frequency, for a fixed time, can become negative which does not make any sense [8]. Additionally, it is very difficult to explain negative probabilities.
2.2.3. Positive TFDs
They produce non-negative TFD of a signal, and do not contain any cross terms. Cohen and Posch [8] demonstrate the existence of an infinite set of positive TFDs, and developed formulations to compute the positive TFDs based on signal-dependent kernels. However, in order to calculate these kernels, the method requires the signal equation which is not known in most of the cases. Therefore, although positive TFDs exist, their derivation process is very complicated to implement.
2.2.4. Matching Pursuit TFD
(MP-TFD) is constructed from matching pursuit as proposed by Mallat and Zhang [2] in 1993. As shown in (3), matching pursuit decomposes a signal into Gabor atoms with a wide variety of frequency modulated, phase and time shift, and duration. After  iteration, the selected components may be concluded to represent coherent structures, and the residue represents incoherent structures in the signal. The residue may be assumed to be due to random noise, since it does not show any TF localization. Therefore, in MP-TFD, the decomposition residue in (3) is ignored, and the WVD of each
iteration, the selected components may be concluded to represent coherent structures, and the residue represents incoherent structures in the signal. The residue may be assumed to be due to random noise, since it does not show any TF localization. Therefore, in MP-TFD, the decomposition residue in (3) is ignored, and the WVD of each  component is added as the following:
component is added as the following:

where  is the WVD of the Gabor atom
is the WVD of the Gabor atom  , and
, and  is the constructed MP-TFD. As previously mentioned, the WVD is a powerful TF representation; however when more than one component is present in the signal, the TF resolution will be confounded by cross terms. In MP-TFD, we apply the WVD to single components and add them up, therefore, the summation will be a cross-term free distribution.
is the constructed MP-TFD. As previously mentioned, the WVD is a powerful TF representation; however when more than one component is present in the signal, the TF resolution will be confounded by cross terms. In MP-TFD, we apply the WVD to single components and add them up, therefore, the summation will be a cross-term free distribution.
Despite the potential advantages of TFD to quantify nonstationary information of real world signals, they have been mainly used for visualization purposes. We review the TFD quantification in the next section, and then we explain our proposed TFD quantification method.
2.3. TFD-Based Quantification
There have been some attempts in literature to TF quantification by removing the redundancy and keeping only the representative parts of the TFD. In [9], the authors consider the TF representation of music signals as texture images, and then they look for the repeating patterns of a given instrument as the representative feature of that instrument. This approach is useful for music signals; however, it is not very efficient for environmental sound classification, where we can not assume the presence of such a structured TF patterns.
Another TF quantification approach is obtaining the instantaneous features from the TFD. One of the first works in this area is the work of Tacer and Loughlin [10], in which Tacer and Loughlin derive two-dimensional moments of the TF plane as features. This approach simply obtains one instantaneous feature for every temporal sample as related to spectral behavior of the signal at each point. However, the quantity of the features is still very large. In [11, 12], instead of directly applying the instantaneous features in the classification process, some statistical properties of these features (e.g., mean and variance) are used. Although this solution reduces the dimension of instantaneous features, its shortcoming is that the statistical analysis diminishes the temporal localization of the instantaneous features.
In a recent approach, the TFD is considered as a matrix, and then a matrix decomposition (MD) technique is applied to the TF matrix (TFM) to derive the significant TF components. This idea has been used for separating instruments in music [13, 14], and has been recently used for music classification [15]. In this approach, the base components are used as feature vectors. The major disadvantage of this method is that the decomposed base vectors have a high dimension, and as a result they are not very appealing features for classification purposes.
Figure 2 depicts our proposed TF quantification approach. As shown in this figure, signal ( ) is transformed into TF matrix
) is transformed into TF matrix  , where
, where  is the TFD of signal
is the TFD of signal  (
( ). Next, a MD is applied to the TFM to decompose the TF matrix into its base and coefficient matrices (
). Next, a MD is applied to the TFM to decompose the TF matrix into its base and coefficient matrices ( and
and  , resp.) in a way that
, resp.) in a way that  . We then extract some features from each vector of the base matrix, and use them as joint TF features of the signal (
. We then extract some features from each vector of the base matrix, and use them as joint TF features of the signal ( ). This approach significantly reduces the dimensionality of the TFD compared to the previous TF quantification approaches. We call the proposed methodology as TFM decomposition feature extraction technique. In our previous paper [16], we applied TF decomposition feature extraction methodology to speech signals in order to automatically identify and measure the speech pathology problem. We extracted meaningful and unique features from both base and coefficient matrices. In this work, we showed that the proposed method extracts meaningful and unique joint TF features from speech, and automatically identifies and measures the abnormality of the signal. We employed TFM decomposition technique to quantify TFD, and proposed novel features for environmental audio signal classification [17]. Our aim in the present work is to extract novel TF features, based on TFM decomposition technique in an attempt to increase the accuracy of the environmental audio classification.
). This approach significantly reduces the dimensionality of the TFD compared to the previous TF quantification approaches. We call the proposed methodology as TFM decomposition feature extraction technique. In our previous paper [16], we applied TF decomposition feature extraction methodology to speech signals in order to automatically identify and measure the speech pathology problem. We extracted meaningful and unique features from both base and coefficient matrices. In this work, we showed that the proposed method extracts meaningful and unique joint TF features from speech, and automatically identifies and measures the abnormality of the signal. We employed TFM decomposition technique to quantify TFD, and proposed novel features for environmental audio signal classification [17]. Our aim in the present work is to extract novel TF features, based on TFM decomposition technique in an attempt to increase the accuracy of the environmental audio classification.
This block diagram represents the TFM quantification technique. In this approach, first the TFD (V K×N ) of a signal (x(t)) is estimated. Then a MD technique decomposes the estimated TF matrix into r bases components (W K×r and H r×N ). Finally, a discriminant and representative feature vector F is extracted from each decomposed component.
2.4. TFM Decomposition
The TFM of a signal  is denoted with
is denoted with  , where
, where  is signal length and
is signal length and  is frequency resolution in the TF analysis. An MD technique with
is frequency resolution in the TF analysis. An MD technique with  decomposition is applied to a matrix in such a way that each element in the TFM can be written as follows:
decomposition is applied to a matrix in such a way that each element in the TFM can be written as follows:

where the decomposed TF matrices,  and
and  , are defined as:
, are defined as:

In (6), MD reduces the TF matrix ( ) to the base and coefficient vectors (
) to the base and coefficient vectors ( and
and  , resp.) in a way that the former represents the spectral components in the TF signal structure, and the latter indicates the location of the corresponding spectral component in time.
, resp.) in a way that the former represents the spectral components in the TF signal structure, and the latter indicates the location of the corresponding spectral component in time.
There are several well-known MD techniques in literature, for example, Principal Component Analysis (PCA), Independent Component Analysis (ICA), and Non-negative Matrix Factorization (NMF). Each MD technique considers different sets of criteria to choose the decomposed matrices with the desired properties, for example, PCA finds a set of orthogonal bases that minimize the mean squared error of the reconstructed data; ICA is a statistical technique that decomposes a complex dataset into components that are as independent as possible; and NMF technique is applied to a non-negative matrix, and decomposes the matrix to its non-negative components.
A MD technique is suitable for TF quantification that the decomposed matrices produce representative and meaningful features. In this work, we choose NMF as the MD method because of the following two reasons.
 In a previous study [18], we showed that the NMF components promise a higher representation and localization property compared to the other MD techniques. Therefore, the features extracted from the NMF component represent the TFM with a high-time and-frequency localization.
In a previous study [18], we showed that the NMF components promise a higher representation and localization property compared to the other MD techniques. Therefore, the features extracted from the NMF component represent the TFM with a high-time and-frequency localization.
 NMF decomposes a matrix into non-negative components. Negative spectral and temporal distributions are not physically interpretable and therefore do not result in meaningful features. Since PCA and ICA techniques do not guarantee the non-negativity of the decomposed factors, instead of directly using
NMF decomposes a matrix into non-negative components. Negative spectral and temporal distributions are not physically interpretable and therefore do not result in meaningful features. Since PCA and ICA techniques do not guarantee the non-negativity of the decomposed factors, instead of directly using  and
and  matrices to extract features, their squared values,
matrices to extract features, their squared values,  and
and  are used [19]. In other words, rather than extracting the features from
are used [19]. In other words, rather than extracting the features from  , the features are extracted from TFM of
, the features are extracted from TFM of  as defined below
as defined below

It can be shown that  , and the negative elements of
, and the negative elements of  and
and  cause artifacts in the extracted TF features. NMF is the only MD techniques that guarantees the non-negativity of the decomposed factors and it therefore is a better MD technique to extract meaningful features compared to ICA and PCA. Therefore, NMF is chosen as the MD technique in TFM decomposition.
cause artifacts in the extracted TF features. NMF is the only MD techniques that guarantees the non-negativity of the decomposed factors and it therefore is a better MD technique to extract meaningful features compared to ICA and PCA. Therefore, NMF is chosen as the MD technique in TFM decomposition.
NMF algorithm starts with an initial estimate for  and
and  , and performs an iterative optimization to minimize a given cost function. In [20], Lee and Seung introduce two updating algorithms using the least square error and the Kullback-Leibler (KL) divergence as the cost functions.
, and performs an iterative optimization to minimize a given cost function. In [20], Lee and Seung introduce two updating algorithms using the least square error and the Kullback-Leibler (KL) divergence as the cost functions.

In these equations,  and
and  are term by term multiplication and division of two matrices. Various alternative minimization strategies for NMF decomposition have been proposed in [21, 22]. In this work, we use a projected gradient bound-constrained optimization method by Lin in [23]. The gradient-based NMF is computationally competitive and offers better convergence properties than the standard approach.
are term by term multiplication and division of two matrices. Various alternative minimization strategies for NMF decomposition have been proposed in [21, 22]. In this work, we use a projected gradient bound-constrained optimization method by Lin in [23]. The gradient-based NMF is computationally competitive and offers better convergence properties than the standard approach.
We apply the TFM decomposition of the audio signals to perform environmental audio classification as is explained in Section 4.2.
3. Audio Coding
In order to address the high demand for audio compression, over the years many compression methodologies were introduced to reduce the bit rates without sacrificing much of the audio quality. Since it is out of scope of this paper to cover all of the existing audio compression methodologies, the authors recommend the work of Painter and Spanias in [24] for a comprehensive review of most of the existing audio compression techniques. Audio signals are highly nonstationary in nature and the best way to analyze them is to use a joint TF approach. The presented coding methodology is based on ATFT and falls under the transform-like coder category. The usual methodology of a transform-based coding technique involves the following steps: (i) transforming the audio signal into frequency or TF-domain coefficients, (ii) processing the coefficients using psychoacoustic models and computing the audio masking thresholds, (iii) controlling the quantizer resolution using the masking thresholds, (iv) applying intelligent bit allocation schemes, and (v) enhancing the compression ratio with further lossless compression schemes. The ATFT-based coder nearly follows the above general transform coder methodology; however, unlike the existing techniques, the major part of the compression was achieved by exploiting the joint TF properties of the audio signals. The block diagram of the ATFT coder is shown in Figure 3. The ATFT approach provides higher TF resolution than the existing TF techniques such as wavelets and wavelet packets [2]. This high-resolution sparse decomposition enables us to achieve a compact representation of the audio signal in the transform domain itself. Also, due to the adaptive nature of the ATFT, there was no need for signal segmentation.
Psychoacoustics were applied in a novel way on the TF decomposition parameters to achieve further compression. In most of the existing audio coding techniques the fundamental decomposition components or building blocks are in the frequency domain with corresponding energy associated with them. This makes it much easier for them to adapt the conventional, well-modeled psychoacoustics techniques into their encoding schemes. On the other hand, in ATFT, the signal was modeled using TF functions which have a definite time and frequency resolution (i.e., each individual TF function is time limited and band limited), hence the existing psychoacoustics models need to be adapted to apply on the TF functions [25].
3.1. ATFT of Audio Signals
Any signal could be expressed as a combination of coherent and noncoherent signal structures. Here the term coherent signal structures means those signal structures that have a definite TF localization (or) exhibit high correlation with the TF dictionary elements. In general, the ATFT algorithm models the coherent signal structures well within the first few 100 iterations, which in most cases contribute to >90% of the signal energy. On the other hand, the noncoherent noise-like structures cannot be easily modeled since they do not have a definite TF localization or correlation with dictionary elements. Hence these noncoherent structures are broken down by the ATFT into smaller components to search for coherent structures. This process is repeated until the whole residue information is diluted across the whole TF dictionary [2]. From a compression point of view, it would be desirable to keep the number of iterations  , as low as possible and at the same time sufficient enough to model the audio signal without introducing perceptual distortions. Considering this requirement, an adaptive limit has to be set for controlling the number of iterations. The energy capture rate (signal energy capture rate per iteration) could be used to achieve this. By monitoring the cumulative energy capture over iterations we could set a limit to stop the decomposition when a particular amount of signal energy was captured. The minimum number of iterations required to model an audio signal without introducing perceptual distortions depends on the signal composition and the length of the signal. In theory, due to the adaptive nature of the ATFT decomposition, it is not necessary to segment the signals. However, due to the computational resource limitations (Pentium III, 933 MHZ with 1 GB RAM), we decomposed the audio signals in 5 s durations. The larger the duration decomposed, the more efficient is the ATFT modeling. This is because if the signal is not sufficiently long, we cannot efficiently utilise longer TF functions (highest possible scale) to approximate the signal. As the longer TF functions cover larger signal segments and also capture more signal energy in the initial iterations, they help to reduce the total number of TF functions required to model an audio signal. Each TF function has a definite time and frequency localization, which means all the information about the occurrences of each of the TF functions in time and frequency of the signal is available. This flexibility helps us later in our processing to group the TF functions corresponding to any short time segments of the audio signal for computing the psychoacoustic thresholds. In other words, the complete length of the audio signal can be first decomposed into TF functions and later the TF functions corresponding to any short time segment of the signal can be grouped together. In comparison, most of the DCT- and MDCT-based existing techniques have to segment the signals into time frames and process them sequentially. This is needed to account for the non-stationarity associated with the audio signals and also to maintain a low signal delay in encoding and decoding.
, as low as possible and at the same time sufficient enough to model the audio signal without introducing perceptual distortions. Considering this requirement, an adaptive limit has to be set for controlling the number of iterations. The energy capture rate (signal energy capture rate per iteration) could be used to achieve this. By monitoring the cumulative energy capture over iterations we could set a limit to stop the decomposition when a particular amount of signal energy was captured. The minimum number of iterations required to model an audio signal without introducing perceptual distortions depends on the signal composition and the length of the signal. In theory, due to the adaptive nature of the ATFT decomposition, it is not necessary to segment the signals. However, due to the computational resource limitations (Pentium III, 933 MHZ with 1 GB RAM), we decomposed the audio signals in 5 s durations. The larger the duration decomposed, the more efficient is the ATFT modeling. This is because if the signal is not sufficiently long, we cannot efficiently utilise longer TF functions (highest possible scale) to approximate the signal. As the longer TF functions cover larger signal segments and also capture more signal energy in the initial iterations, they help to reduce the total number of TF functions required to model an audio signal. Each TF function has a definite time and frequency localization, which means all the information about the occurrences of each of the TF functions in time and frequency of the signal is available. This flexibility helps us later in our processing to group the TF functions corresponding to any short time segments of the audio signal for computing the psychoacoustic thresholds. In other words, the complete length of the audio signal can be first decomposed into TF functions and later the TF functions corresponding to any short time segment of the signal can be grouped together. In comparison, most of the DCT- and MDCT-based existing techniques have to segment the signals into time frames and process them sequentially. This is needed to account for the non-stationarity associated with the audio signals and also to maintain a low signal delay in encoding and decoding.
In the presented technique for a signal duration of 5 s, the decomposition limit was set to be the number of iterations ( ) needed to capture
) needed to capture  of the signal energy or to a maximum of 10,000 iterations and is given by
of the signal energy or to a maximum of 10,000 iterations and is given by

For a signal with less noncoherent structures,  of signal energy could be modeled with a lower number of TF functions than a signal with more noncoherent structures. In most cases a
of signal energy could be modeled with a lower number of TF functions than a signal with more noncoherent structures. In most cases a  of energy capture nearly characterises the audio signal completely. The upper limit of the iterations is fixed to 10,000 iterations to reduce the computational load. Figure 4 demonstrates the number of TF functions needed for a sample audio signal. In the figure, the lower panel shows the energy capture curve for the sample audio signal in the top panel with number of TF functions in the
of energy capture nearly characterises the audio signal completely. The upper limit of the iterations is fixed to 10,000 iterations to reduce the computational load. Figure 4 demonstrates the number of TF functions needed for a sample audio signal. In the figure, the lower panel shows the energy capture curve for the sample audio signal in the top panel with number of TF functions in the  -axis and the normalised energy in the
-axis and the normalised energy in the  -axis. On average, it was observed that 6000 TF functions are needed to represent a signal of 5 s duration sampled at 44.1 kHz.
-axis. On average, it was observed that 6000 TF functions are needed to represent a signal of 5 s duration sampled at 44.1 kHz.
3.2. Implementation of Psychoacoustics
In the conventional coding methods, the signal is segmented into short time segments and transformed into frequency domain coefficients. These individual frequency components are used to compute the psychoacoustic masking thresholds and accordingly their quantization resolutions are controlled. In contrast, in our approach we computed the psychoacoustic masking properties of individual TF functions and used them to decide whether a TF function with certain energy was perceptually relevant or not based on its time occurrence with other TF functions. TF functions are the basic components of the presented technique and each TF function has a certain time and frequency support in the TF plane. So their psychoacoustical properties have to be studied by taking them as a whole to arrive at a suitable psychoacoustical model. More details on the implementation of psychoacoustics is covered in [25, 26].
3.3. Quantization
Most of the existing transform-based coders rely on controlling the quantizer resolution based on psychoacoustic thresholds to achieve compression. Unlike this, the presented technique achieves a major part of the compression in the transformation itself followed by perceptual filtering. That is, when the number of iterations  needed to model a signal is very low compared to the length of the signal, we just need
needed to model a signal is very low compared to the length of the signal, we just need  bits. Where
bits. Where  is the number of bits needed to quantize the 5 TF parameters that represent a TF function. Hence, we limited our research work to scalar quantizers as the focus of the research mainly lies on the TF transformation block and the psychoacoustics block rather than the usual sub-blocks of the data compression application.
is the number of bits needed to quantize the 5 TF parameters that represent a TF function. Hence, we limited our research work to scalar quantizers as the focus of the research mainly lies on the TF transformation block and the psychoacoustics block rather than the usual sub-blocks of the data compression application.
As explained earlier each of the five parameters Energy ( ), Center frequency (
), Center frequency ( ), Time position (
), Time position ( ), Octave (
), Octave ( ), and Phase (
), and Phase ( ) are needed to represent a TF function and thereby the signal itself. These five parameters were to be quantized in such a way that the quantization error introduced was imperceptible while, at the same time, obtaining good compression. Each of the five parameters has different characteristics and dynamic range. After careful analysis of them the following bit allocations were made. In arriving at the final bit allocations informal Mean Opinions Score (MOS) tests were conducted to compare the quality of the audio samples before and after quantization stage.
) are needed to represent a TF function and thereby the signal itself. These five parameters were to be quantized in such a way that the quantization error introduced was imperceptible while, at the same time, obtaining good compression. Each of the five parameters has different characteristics and dynamic range. After careful analysis of them the following bit allocations were made. In arriving at the final bit allocations informal Mean Opinions Score (MOS) tests were conducted to compare the quality of the audio samples before and after quantization stage.
In total, 54 bits are needed to represent each TF function without introducing significant perceptual quantization noise in the reconstructed signal. The final form of data for  TF functions will contain the following.
TF functions will contain the following.
-
(i)
Energy parameter (Log companded) =
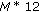 bits.
bits. -
(ii)
Time position parameter =
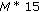 bits.
bits. -
(iii)
Center frequency parameter =
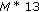 bits.
bits. -
(iv)
Phase parameter =
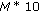 bits.
bits. -
(v)
Octave parameter =
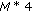 bits.
bits.
The sum of all the above ( bits) will be the total number of bits transmitted or stored representing an audio segment of duration 5 s. The energy parameter after log companding was observed to be a very smooth curve. Fitting a curve to the energy parameter further reduces the bit rate [25, 26]. With just a simple scalar quantizer and curve fitting of the energy parameter, the presented coder achieves high-compression ratios. Although a scalar quantizer was used to reduce the computational complexity of the presented coder, sophisticated vector quantization techniques can be easily incorporated to further increase the coding efficiency. The 5 parameters of the TF function can be treated as one vector and accordingly quantized using predefined codebooks. Once the vector is quantized, only the index of the codebook needs to be transmitted for each set of TF parameters resulting in a large reduction of the total number of bits. However designing the codebooks would be challenging as the dynamic ranges of the 5 TF parameters are drastically different. Apart from reducing the number of total bits, the quantization stage can also be utilized to control the bit rates suitable for CBR (Constant Bit Rate) applications.
bits) will be the total number of bits transmitted or stored representing an audio segment of duration 5 s. The energy parameter after log companding was observed to be a very smooth curve. Fitting a curve to the energy parameter further reduces the bit rate [25, 26]. With just a simple scalar quantizer and curve fitting of the energy parameter, the presented coder achieves high-compression ratios. Although a scalar quantizer was used to reduce the computational complexity of the presented coder, sophisticated vector quantization techniques can be easily incorporated to further increase the coding efficiency. The 5 parameters of the TF function can be treated as one vector and accordingly quantized using predefined codebooks. Once the vector is quantized, only the index of the codebook needs to be transmitted for each set of TF parameters resulting in a large reduction of the total number of bits. However designing the codebooks would be challenging as the dynamic ranges of the 5 TF parameters are drastically different. Apart from reducing the number of total bits, the quantization stage can also be utilized to control the bit rates suitable for CBR (Constant Bit Rate) applications.
3.4. Compression Ratios
Compression ratios achieved by the presented coder were computed for eight sample wideband audio signals (of 5 s duration) as described below. These eight sample signals (namely, ACDC, DEFLE, ENYA, HARP, HARPSICHORD, PIANO, TUBULARBELL, and VISIT) were representatives of wide range of music types.
-
(i)
As explained earlier, the total number of bits needed to represent each TF function is 54.
-
(ii)
The energy parameter is curve fitted and only the first 150 points in addition to the curve fitted point need to be coded.
-
(iii)
So the total number of bits needed for
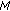 iterations for a 5 s duration of the signal is
iterations for a 5 s duration of the signal is 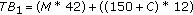 , where
, where  is the number of curve fitted points, and
is the number of curve fitted points, and 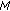 is the number of perceptually important functions.
is the number of perceptually important functions. -
(iv)
The total number of bits needed for a CD quality 16 bit PCM technique for a 5 s duration of the signal sampled at 44100 Hz is
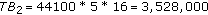 .
. -
(v)
The compression ratio can be expressed as the ratio of number of bits needed by the presented coder to the number of bits needed by the CD quality 16 bit PCM technique for the same length of the signal, that is,
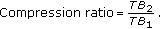 (11)
(11) -
(vi)
The overall compression ratio for a signal was then calculated by averaging all the 5 s duration segments of the signal for both the channels.
The presented coder is based on an adaptive signal transformation technique, that is, the content of the signal and the dictionary of basis functions used to model the signal play an important role in determining how compact a signal can be represented (compressed). Hence, VBR (Variable Bit Rate) is the best way to present the performance benefit of using an adaptive decomposition approach. The inherent variability introduced in the number of TF functions required to model a signal and thereby the compression is one of the highlights of using ATFT. Although VBR would be more appropriate to present the performance benefit of the presented coder, CBR mode has its own advantages when using with applications that demand network transmissions over constant bitrate channels with limited delays. The presented coder can also be used in CBR mode by fixing the number of TF functions used for representing signal segments, however due to the signal adaptive nature of the presented coder this would compromise the quality at instances where signal segments demand a higher number of TF functions for perceptually lossless reproduction. Hence we choose to present the results of the presented coder using only the VBR mode.
We compared the presented coder with two existing popular and state-of-the-art audio coders, namely, MP3 (MPEG 1 layer 3) and MPEG-4 AAC/HE-AAC. Advanced audio coding (AAC) is the current industrial standard which was initially developed for multichannel surround signals (MPEG-2 AAC [27]). As there are ample studies in the literature [27–32] available for both MP3 and MPEG-2/4 AAC more details about these techniques are not provided in this paper. The average bit rates were used to calculate the compression ratio achieved by MP3 and MPEG-4 AAC as described below.
-
(i)
Bitrate for a CD quality 16 bit PCM technique for 1 s stereo signal is given by
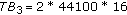 .
. -
(ii)
The average bit rate/s achieved by (MP3 or MPEG-4 AAC) in VBR mode =
 .
. -
(iii)
Compression ratio achieved by (MP3 or MPEG-4 AAC) =
 .
.
The 2nd, 4th and 6th columns of Table 1 show the compression ratio (CR) achieved by the MP3, MPEG-4 AAC and the presented ATFT coders for the set of 8 sample audio files. It is evident from the table that the presented coder has better compression ratios than MP3. When comparing with MPEG-4 AAC, 5 out of 8 signals are either comparable or have better compression ratios than the MPEG-4 AAC. It is noteworthy to mention that for slow music (classical type) the ATFT coder provides 3 to 4 times better comparison than MPEG-4 AAC or MP3.
The compression ratio alone cannot be used to evaluate an audio coder. The compressed audio signals has to undergo a subjective evaluation to compare the quality achieved with respect to the original signal. The combination of the subjective rating and the compression ratio will provide a true evaluation of the coder performance.
Before performing the subjective evaluation, the signal has to be reconstructed. The reconstruction process is a straightforward process of linearly adding all the TF functions with their corresponding five TF parameters. In order to do that, first the TF parameters modified for reducing the bit rates have to be expanded back to their original forms. The log compressed energy curve was log expanded after recovering back all the curve points using interpolation on the equally placed 50 length points. The energy curve was multiplied with the normalization factor to bring the energy parameter as it was during the decomposition of the signal. The restored parameters (Energy, Time-position, Center frequency, Phase and Octave) were fed to the ATFT algorithm to reconstruct the signal. The reconstructed signal was then smoothed using a 3rd-order Savitzky-Golay [33] filter and saved in a playable format.
Figure 5 demonstrates a sample signal (/"HARP"/) and its reconstructed version and the corresponding spectrograms. It can be clearly observed from the reconstructed signal spectrogram compared with the original signal spectrogram, how accurately the ATFT technique has filtered out the irrelevant components from the signal (evident from Table 1—(/"HARP"/)—high-compression ratio versus acceptable quality). The accuracy in adaptive filtering of the irrelevant components is made possible by the TF resolution provided by the ATFT algorithm.
Example of a sample original (/"HARP"/) and the reconstructed signal with their respective spectrograms.X-axes for the original and reconstructed signal are in time samples, and X-axes for the spectrogram of the original and the reconstructed signal are in equivalent time in seconds. Note that the sampling frequency = 44.1 kHz. au: arbitrary units.
3.5. Subjective Evaluation of ATFT Coder
Subjective evaluation of audio quality is needed to assess the audio coder performance. Even though there are objective measures such as SNR, total harmonic distortion (THD), and Noise-to-mask ratio [34] they would not give a true evaluation of the audio codec particularly if they use lossy schemes as in the proposed technique. This is due to the fact say, for example, in a perceptual coder, SNR is lost however audio quality is claimed to be perceptually lossless. In this case SNR measure may not give the correct performance evaluation of the coder.
We used the subjective evaluation method recommended by ITU-R standards (BS. 1116). It is called a "double blind triple stimulus with hidden reference" [24, 34]. A Subjective Difference Grade (SDG) [24] was computed by subtracting the absolute score assigned to the hidden reference audio signal from the absolute score assigned to the compressed audio signal. It is given by

Accordingly the scale of SDG will range from (−4 to 0) with the following interpretation: (−4): Unsatisfactory (or) Very Annoying, (−3): Poor (or) Annoying, (−2): Fair (or) Slightly annoying, (−1): Good (or) Perceptible but not annoying, and  : Excellent (or) Imperceptible. Fifteen listeners (randomly selected) participated in the MOS studies and evaluated all the 3 audio coders (MP3, AAC and ATFT in VBR mode). The average SDG was computed for each of the audio sample. The 3rd, 5th and 7th columns of the Table 1 show the SDGs obtained for MP3, AAC and ATFT coders, respectively. MP3 and AAC SDGs fall very close to the Imperceptible
: Excellent (or) Imperceptible. Fifteen listeners (randomly selected) participated in the MOS studies and evaluated all the 3 audio coders (MP3, AAC and ATFT in VBR mode). The average SDG was computed for each of the audio sample. The 3rd, 5th and 7th columns of the Table 1 show the SDGs obtained for MP3, AAC and ATFT coders, respectively. MP3 and AAC SDGs fall very close to the Imperceptible  region, whereas the proposed ATFT SDGs are spread out between −0.53 to −2.27.
region, whereas the proposed ATFT SDGs are spread out between −0.53 to −2.27.
3.6. Results and Discussion
The compression ratios (CRs) and the SDG for all three coders (MP3, AAC and ATFT) are shown in Table 1. All the coders were tested in the VBR mode. For the presented technique, VBR was the best way to present the performance benefit of using an adaptive decomposition approach. In ATFT, the type of the signal and the characteristics of the TF functions (type of dictionary) control the number of transformation parameters required to approximate the signal and thereby the compression ratio. The inherent variability introduced in the number of TF functions required to model a signal is one of the highlights of using ATFT. Hence we choose to present comparison of the coders in the VBR mode.
The results show that the MP3 and AAC coders perform well with excellent SDG scores (Imperceptible) at a compression ratio around 10. The presented coder does not perform well with all of the eight samples. Out of the 8 samples, 6 samples have an SDG between −0.53 to −1 (Imperceptible—perceptible but not annoying) and 2 samples have SDG below −1. Out of the 6 samples with SDGs between (−0.53 and −1), 3 samples (ENYA, HARP and PIANO) have compression ratios 2 to 4 times higher than MP3 and AAC and 3 samples (ACDC, HARPSICHORD and TUBULARBELL) have comparable compression ratios with moderate SDGs.
Figure 6 shows the comparison of all three coders by plotting the samples with their SDGs in  -axis and compression ratios in the
-axis and compression ratios in the  -axis. If we can virtually divide this plot in segments of SDGs (horizontally) and the compression ratios (vertically), then the ideal desirable coder performance should be in the right top corner of the plot (high-compression ratios and excellent SDG scores). This is followed next by the right bottom corner (low-compression ratios and excellent SDG scores) and so on as we move from right to left in the plot. Here the terms "Low"- and "High"-compression ratios are used in a relative sense based on the compression ratios achieved by all the 3 coders in this study. From the plot it can be seen that MP3 and AAC coders occupy the right bottom corner, whereas the samples from ATFT coder are spread over. As mentioned earlier 3 out the 8 samples of the ATFT coder occupy the right top corner only with moderate SDGs that are much less than the MP3 and the AAC. 3 out of the remaining 5 samples of the ATFT coder occupy the right bottom corner, again with only moderate SDGs that are less than MP3 and AAC. The remaining 2 samples perform the worst occupying the left bottom corner.
-axis. If we can virtually divide this plot in segments of SDGs (horizontally) and the compression ratios (vertically), then the ideal desirable coder performance should be in the right top corner of the plot (high-compression ratios and excellent SDG scores). This is followed next by the right bottom corner (low-compression ratios and excellent SDG scores) and so on as we move from right to left in the plot. Here the terms "Low"- and "High"-compression ratios are used in a relative sense based on the compression ratios achieved by all the 3 coders in this study. From the plot it can be seen that MP3 and AAC coders occupy the right bottom corner, whereas the samples from ATFT coder are spread over. As mentioned earlier 3 out the 8 samples of the ATFT coder occupy the right top corner only with moderate SDGs that are much less than the MP3 and the AAC. 3 out of the remaining 5 samples of the ATFT coder occupy the right bottom corner, again with only moderate SDGs that are less than MP3 and AAC. The remaining 2 samples perform the worst occupying the left bottom corner.
We analyzed the poorly performing ATFT coded signals DEFLE and VISIT. DEFLE is a rapidly varying rock-like signal with minimal voice components and VISIT is a signal with dominant voice components. We observed that the symmetrical and smooth Gaussian dictionary used in this study does not model the transients well, which are the main features of all rapidly varying signals like DEFLE. This inefficient modeling of transients by the symmetrical Gaussian TF functions resulted in the poor SDG for the DEFLE. A more appropriate dictionary would be a damped sinusoids dictionary [35] which can better model the transient-like decaying structures in audio signals. However a single dictionary alone may not be sufficient to model all types of signal structures. The second signal VISIT has significant amount(s) of voice components. Even though the main voice components are modeled well by the ATFT, the noise-like hissing and shrilling sounds (noncoherent structures) could not be modeled within the decomposition limit of 10,000 iterations. These hissing and shrilling sounds actually add to the pleasantness of the music. Any distortion in them is easily perceived which could have reduced the SDG of the signal to the lowest of the group −2.27. The poor performances with the two audio sample cases could be addressed by using a hybrid dictionary of TF functions and residue coding the noncoherent structures separately. However this would increase the computational complexity of the coder and reduce the compression ratios.
We have covered most details involved in a stage by stage implementation and evaluation of a transform-based audio coder. The approach demonstrated the application of ATFT for audio coding and the development of a novel psychoacoustics model adapted to TF functions. The compression strategy was changed from the conventional way of controlling quantizer resolution to achieving majority of the compression in the transformation itself. Listening tests were conducted and the performance comparison of the presented coder with MP3 and AAC coders were presented. From the preliminary results, although the proposed coder achieves high-compression ratios, its SDG scores are well below the MP3 and AAC family of coders. The proposed coder however performs moderately well for slowly varying classical type signals with acceptable SDGs. The proposed coder is not as refined as the state-of-the-art commercial coders, which to some extent explains its poor performance.
From the results presented for the ATFT coder, the signal adaptive performance of the coder for a specific TF dictionary is evident, that is, with a Gaussian TF dictionary the coder performed moderately well for slow-varying classical signals than fast varying rock-like signals. In other words the ATFT algorithm demonstrated notable differences in the decomposition patterns of classical and rock-like signals. This is a valid clue and a motivating factor that these differences in the decomposition patterns if quantified using TF decomposition parameters could be used as discriminating features for classifying audio signals. We apply this hypothesis in extracting TF features for classifying audio signals for a content-based audio retrieval application as will be explained in Section 4.
3.7. Summary of Steps Involved in Implementing ATFT Audio Coder
Step 1 (ATFT algorithm and TF dictionaries).
Existing implementation of Matching Pursuits can be adapted for the purposes;  LastWave (http://www.cmap.polytechnique.fr/~bacry/LastWave/),
LastWave (http://www.cmap.polytechnique.fr/~bacry/LastWave/),  Matching Pursuit Package (MPP) (ftp://cs.nyu.edu/pub/wave/software/mpp.tar.Z), and
Matching Pursuit Package (MPP) (ftp://cs.nyu.edu/pub/wave/software/mpp.tar.Z), and  Matching Pursuit ToolKit (MPTK) [36].
Matching Pursuit ToolKit (MPTK) [36].
Step 2 (Control decomposition).
The number of TF functions required to model a fixed segment of audio signal can be arrived using similar criteria described in Section 3.1.
Step 3 (Perceptual Filtering).
The TF functions obtained from Step 2 can be further filtered using the psychoacoustics thresholds discussed in Section 3.2.
Step 4 (Quantization).
The simple quantization scheme presented in Section 3.3 can be used for bit allocation or advanced vector quantization methods can also be explored.
Step 5 (Lossless schemes).
Further lossless schemes can be applied to the quantized TF parameters to further increase the compression ratio.
4. Audio Classification
Audio feature extraction plays an important role in analyzing and characterizing audio content. Auditory scene analysis, content-based retrieval, indexing, and fingerprinting of audio are few of the applications that require efficient feature extraction. The general methodology of audio classification involves extracting discriminatory features from the audio data and feeding them to a pattern classifier. Different approaches and various kinds of audio features were proposed with varying success rates. Audio feature extraction serves as the basis for a wide range of applications in the areas of speech processing [37], multimedia data management and distribution [38–41], security [42], biometrics and bioacoustics [43]. The features can be extracted either directly from the time-domain signal or from a transformation domain depending upon the choice of the signal analysis approach. Some of the audio features that have been successfully used for audio classification include mel frequency cepstral coefficients (MFCCs) [40, 41], spectral similarity [44], timbral texture [41], band periodicity [38], LPCC (Linear Prediction Coefficient-derived cepstral coefficients) [45], zero crossing rate [38, 45], MPEG-7 descriptors [46], entropy [12], and octaves [39]. Few techniques generate a pattern from the features and use it for classification by the degree of correlation. Few other techniques use the numerical values of the features coupled to statistical classification methods.
4.1. Music Classification
In this section, we present a content-based audio retrieval application employing audio classification and explain the generic steps involved in performing successful audio classification. The simplest of all retrieval techniques is the text-based searching where the information about the multimedia data is stored with the data file. However the success of these type of text-based searches depend on how well they are text indexed by the author and they do not provide any information on the real content of the data. To make the retrieval system automated, efficient, and intelligent, content-based retrieval techniques were introduced. The presented work focuses on one such way for automatic classification of audio signals for retrieval purposes. The block diagram of the proposed technique is shown in Figure 7.
In content-based retrieval systems, audio data is analyzed, and discriminatory features are extracted. The selection of features depends on the domain of analysis and the perceptual characteristics of the audio signals under consideration. These features are used to generate subspaces dividing the audio signal types to fit in one of the subspaces. The division of subspaces and the level of classification vary from technique to technique. When a query is placed the similarity of the query is checked with all subspaces and the audio signals from the highly correlated subspace is returned as the result. The classification accuracy, and the discriminatory power of the features extracted determine the success of such retrieval systems.
Most of the existing techniques do not take into consideration the true nonstationary behavior of the audio signals while deriving their features. The presented approach uses the same ATFT transform that was discussed in the previous audio coding section. ATFT approach is one of the best ways to handle nonstationary behavior of the audio signals and also due to its adaptive nature, does not require any signal segmentation techniques as used by most of the existing techniques. Unlike many existing techniques where multiple features are used for classification, in the proposed technique, only one TF decomposition parameter is used to generate a feature set from different frequency bands for classification. Due to its strong discriminatory power, just one TF decomposition parameter is sufficient enough for accurate classification of music into six groups.
4.1.1. Audio Database
A database consisting of 170 audio signals was used in the proposed technique. Each audio signal is a segment of 5 s duration extracted from individual original CD music tracks (wide band audio at 44100 samples/second) and no more than one audio signal (5 s duration) was extracted from the same music track. The 170 audio signals consist of 24 rock, 35 classical, 31 country, 21 jazz, 34 folk, and 25 pop signals. As all signals of the database were extracted from commercial CD music tracks, they exhibited all the required characteristics of their respective music genre, such as guitars, drumbeats, vocal, and piano. The signal duration of 5 s was arrived at using the rationale that the longer the audio signal analyzed, the better the extracted feature which exhibits more accurate music characteristics. As the ATFT algorithm is adaptive and does not need any segmentation, theoretically there is no limit for the signal length. However considering the hardware (Pentium III @ 933 MHz and 1.5 GB RAM) limitations of the processing facility, we used 5 s duration samples. In the proposed technique first all the signals were chosen between 15 s to 20 s of the original music tracks. Later by inspection those segments, which were inappropriately selected were replaced by segments (5 s duration) at random locations of the original music track in such way their music genre is exhibited.
4.1.2. Feature Extraction
All the signals were decomposed using the ATFT algorithm. The decomposition parameters provided by the ATFT algorithm were analyzed, and the octave  parameter was observed to contain significant information on different types of music signals. In the decomposition process, the octave or scaling parameter is decided by the adaptive window duration of the Gaussian function that is used in the best possible approximation of the local signal structures. Higher octaves correspond to longer window durations and the lower octaves correspond to shorter window duration. In other words combinations of these octaves represent the envelope of the signal. The envelope (temporal structures) [47] of an audio signal provides valid clues such as rhythmic structure [41], indirect pitch content [41], phonetic composition [48], tonal and transient contributions. Figure 8 demonstrates a sample piece of a music signal and its reconstructed version using 10 TF functions. The relation between the octave parameter and the envelope of the signal is clearly seen. Based on the composition of different structures in a signal, the octave mapping or distribution varies significantly. For example, more lower-order octaves are needed for signals containing lot of transient-like structures and on the other hand more higher-order octaves are needed for signal containing rhythmic tonal components. As an illustration, from Figure 9 it can be observed that signals with similar spectral characteristics exhibit a similar pattern in their octave distribution. Signals 1 and 2 are rock-like music, whereas Signals 3 and 4 are instrumental classical. Comparing the spectrograms with the octave distributions, one can observe that the octave distribution reflecting the spectral similarities for the same category of signals.
parameter was observed to contain significant information on different types of music signals. In the decomposition process, the octave or scaling parameter is decided by the adaptive window duration of the Gaussian function that is used in the best possible approximation of the local signal structures. Higher octaves correspond to longer window durations and the lower octaves correspond to shorter window duration. In other words combinations of these octaves represent the envelope of the signal. The envelope (temporal structures) [47] of an audio signal provides valid clues such as rhythmic structure [41], indirect pitch content [41], phonetic composition [48], tonal and transient contributions. Figure 8 demonstrates a sample piece of a music signal and its reconstructed version using 10 TF functions. The relation between the octave parameter and the envelope of the signal is clearly seen. Based on the composition of different structures in a signal, the octave mapping or distribution varies significantly. For example, more lower-order octaves are needed for signals containing lot of transient-like structures and on the other hand more higher-order octaves are needed for signal containing rhythmic tonal components. As an illustration, from Figure 9 it can be observed that signals with similar spectral characteristics exhibit a similar pattern in their octave distribution. Signals 1 and 2 are rock-like music, whereas Signals 3 and 4 are instrumental classical. Comparing the spectrograms with the octave distributions, one can observe that the octave distribution reflecting the spectral similarities for the same category of signals.
To further improve the discriminatory power of this parameter the distribution of this parameter is grouped into three frequency bands 0–5 kHz, 5–10 kHz, and 10–20 kHz. This is done since analyzing the audio signals in subbands will provide more precise information about their audio characteristics [49]. The bounds for frequency bands were arrived considering the fact that most of the audio content lies well within 10 kHz range so this band needs to be looked more in detail hence broken further into 0–5 kHz and 5 kHz to 10 kHz and the remaining as one band between 10 kHz to 20 kHz. By this frequency division we get an indirect measure of signal envelope contribution from each frequency band. From Figure 9 even though we see difference in the distribution of octaves between rock-like and classical music, it becomes more evident when the distribution is divided into three frequency bands as shown for a sample rock and a classical signal in Figures 10 and 11. Dividing the octave distribution into frequency bands basically reveal the pattern in which the temporal structures occur over the range of frequencies. As music is the combination of different temporal structures with different frequencies occurring at same or different time instants, each type of music exhibit a unique average pattern. Based on the subtle differences between patterns to be detected, the division of octave distribution over fine frequency intervals and the dimension of the feature set can be controlled.
After decomposing all the audio signals using ATFT, the TF functions were grouped into three frequency bands based on their center frequencies  . Then the distribution of each of the 14 octave parameter
. Then the distribution of each of the 14 octave parameter  values were calculated over the 3 frequency bands to get a total of
values were calculated over the 3 frequency bands to get a total of  different distribution values. All these 42 values of each audio segment were used as a feature set for classification. As an illustration, in Figures 10 and 11 the
different distribution values. All these 42 values of each audio segment were used as a feature set for classification. As an illustration, in Figures 10 and 11 the  -axis represents the 14 octave parameters and the
-axis represents the 14 octave parameters and the  -axis represents the distribution of the octave parameters over three frequency bands for 10,000 iterations. Each of the distribution value forms one of 42 elements in the feature set.
-axis represents the distribution of the octave parameters over three frequency bands for 10,000 iterations. Each of the distribution value forms one of 42 elements in the feature set.
4.1.3. Pattern Classification
The motivation for the pattern classification is to automatically group audio signals of same characteristics using the discriminatory features derived as explained in previous subsection.
Pattern classification was carried out by linear discriminant analysis (LDA)-based classifier using the SPSS software [50]. In discriminant analysis, the feature vector derived as explained above were transformed into canonical discriminant functions such as

where  is the set of features,
is the set of features,  and
and  are the coefficients and constant, respectively. The feature dimension
are the coefficients and constant, respectively. The feature dimension  represents the number of features used in the analysis. Using the discriminant scores and the prior probability values of each group, the posterior probabilities of each sample occurring in each of the groups were computed. The sample was then assigned to the group with the highest posterior probability [50].
represents the number of features used in the analysis. Using the discriminant scores and the prior probability values of each group, the posterior probabilities of each sample occurring in each of the groups were computed. The sample was then assigned to the group with the highest posterior probability [50].
The classification accuracy was estimated using the leave-one-out method which is known to provide a least bias estimate [51]. In the leave-one-out method, one sample is excluded from the dataset and the classifier is trained with the remaining samples. Then the excluded signal is used as the test data and the classification accuracy is determined. This is repeated for all samples of the dataset. Since each signal is excluded from the training set in turn, the independence between the test and the training set are maintained.
4.1.4. Results and Discussion
A database of 170 audio signals consisting of 24 rock, 35 classical, 31 country, 21 jazz, 34 folk and 25 pop each of 5 s duration was used. All the 170 audio signals were decomposed and the feature set of 42 octave distribution values were extracted. The extracted feature sets for the entire 170 signals were fed to the classifier based on LDA. Six-group classification was performed (rock, classical, country, jazz, folk and pop). Table 2 shows the confusion matrices for different classification procedures. An overall classification accuracy of 97.6% is achieved by the regular LDA method and 91.2% with the leave-one-out-based LDA method. In the regular LDA method, all the 24 rock, 35 classical, 31 country, and 25 pop were correctly classified with 100% classification accuracy. Two out of 21 jazz and 2 out of 34 folk signals were misclassified with a correct classification accuracy of 90.5% and 94.1%, respectively. The classification accuracy of 91.2% with the leave-one-out method proves the robustness of the proposed technique and independence of the achieved results irrespective of the dataset size. Figure 12 shows the all-groups scatter plot with the first two canonical discriminant functions. One can clearly observe the significant separation between the group spaces explaining the high-discriminatory power of the feature set based on the octave distribution.
The misclassified signals were analyzed but could not identify a clear auditory clue to why they were misclassified. However their differences are observed in the feature set. Considering the known fact that no music genre has clear hard line boundaries and the perceptual boundaries are often subjective (e.g., rock and pop often have overlaps and likewise jazz and classical too have overlaps), we may attribute the classification error of these signals on the natural overlap of the music genre and the amount of knowledge imparted to the classifier with the given database.
In this section, we have covered details involved in a simple audio classification task using a time-frequency approach. The high-classification accuracies achieved by the proposed technique clearly demonstrate the potential of a true nonstationary tool in the form of a joint TF approach for audio classification. More interestingly a single TF decomposition parameter is used for feature extraction proving the high-discriminatory power provided by TF approach compared to the existing techniques.
4.2. Classification of Environmental Sounds
In this section, we present an environmental audio classification. Audio signals are important sources of information for understanding the content of multimedia. Therefore, developing audio classification techniques that better characterize audio signals plays an essential role in many multimedia implications such as (a) multimedia indexing and retrieval, and (b) auditory scene analysis.
4.2.1. Audio Database
The lack of a common dataset does not allow researchers to compare the performance of different audio classification methodologies in a fair manner. Some literatures report an impressive accuracy rate, but they use only a small number of classes and/or a small dataset in their evaluations. The number of classes used in literature varies from study to study. For example, in [52], the authors use two classes (i.e., speech and music) while audio content analysis at Microsoft research [53] uses four audio classes (i.e., speech, music, environment sound, and silence). Freeman et al. [54] uses four classes of speech (i.e., babble, traffic noise, typing, and white noise) while the authors in [55] use 14 different environmental scenes (i.e., inside restaurants, playground, street traffic, train passing, inside moving vehicles, inside casinos, street with police car siren, street with ambulance siren, nature daytime, nature nighttime, Ocean waves, running water, rain, and thunder). In this work we use an environmental audio dataset that was developed and compiled in our signal analysis research (SAR) group at Ryerson University. This database consists of 192 audio signals of 5 s duration each with a sampling rate of 22.05 kHz and a resolution of 16 bits/sample. It is designed to have 10 different classes including 20 aircraft, 17 helicopters, 20 drums, 15 flutes, 20 pianos, 20 animals, 20 birds and 20 insects, and the speech of 20 males and 20 females. Most of the music samples were collected from the Internet and suitably processed to have uniform sampling frequency and duration.
4.2.2. Feature Extraction
All signals were decomposed using the TFM decomposition method. First, we perform the MP-TFD on 3 s duration of each signal, and construct the TFM of each signal. Next, NMF with decomposition order of 15 ( ) is performed on each MP-TF matrix, and 15 base vectors and 15 coefficient vectors are extracted for each signal. Figures 13 and 14 show the decomposition vectors of an aircraft and a piano signal, respectively.
) is performed on each MP-TF matrix, and 15 base vectors and 15 coefficient vectors are extracted for each signal. Figures 13 and 14 show the decomposition vectors of an aircraft and a piano signal, respectively.
(a) and (b) show a segment that belongs to an aircraft signal in time and TF representations, respectively. Applying NMF to the TF matrix, we extract 15 base and coefficient vectors which are depicted in (c) and (d), respectively.Time representationTF representationBase vectors decomposed using NMF MD techniqueCoefficient vectors decomposed using NMF MD technique
(a) and (b) show a segment that belongs to a piano signal in time and TF representations, respectively. Applying NMF to the TF matrix, we extract 15 base and coefficient vectors which are depicted in (c) and (d), respectively.Time representationTF representationBase vectors decomposed using NMF MD techniqueCoefficient vectors decomposed using NMF MD technique
20 features are extracted from each decomposed base and coefficient vector. 13 of the features are the first 13 MFCC of each base vector, and the next six features are  , and
, and  . These features are explained as follows:
. These features are explained as follows:
(a)  and
and  are the sparsity of coefficient and base vectors, respectively. This feature helps to distinguish between transient and continuous components. Several sparseness measures have been proposed and used in the literature. We propose a sparsity function as follows
are the sparsity of coefficient and base vectors, respectively. This feature helps to distinguish between transient and continuous components. Several sparseness measures have been proposed and used in the literature. We propose a sparsity function as follows


The sparsity is zero if and only if a vector contains a single nonzero component, and is negative infinity if and only if all the components are equal. The sparsity measure in (15) has been used for applications such as NMF matrix decomposition with more part-based properties [56]; however, it has never been used for feature extraction application.
(b)  and
and  represent the discontinuities and abrupt changes in each vector. These features are calculated as follows:
represent the discontinuities and abrupt changes in each vector. These features are calculated as follows:

where  and
and  are derivatives of coefficient and base vectors, respectively
are derivatives of coefficient and base vectors, respectively

(c)  and
and  represent the temporal and spectral moments, respectively. Our observation showed that the temporal and spectral spread of the TF energy are discriminant characteristics for different audio groups. To quantify this property, we extract the second moment around the mean of each coefficient and base vectors as follows:
represent the temporal and spectral moments, respectively. Our observation showed that the temporal and spectral spread of the TF energy are discriminant characteristics for different audio groups. To quantify this property, we extract the second moment around the mean of each coefficient and base vectors as follows:

where  and
and  are the mean of the coefficient and base vector
are the mean of the coefficient and base vector  , respectively.
, respectively.
(d)  is the Matching Pursuit Feature. Using
is the Matching Pursuit Feature. Using  iterations of MP, we project an audio signal into a linear combination of Gaussian functions
iterations of MP, we project an audio signal into a linear combination of Gaussian functions  as shown in (3). The amount of signal energy that is projected at each iteration depends on the signal structure. The signal with coherent structure needs less number of iterations, while noncoherent structured signals take more iterations to get decomposed. In order to calculate MP feature in a way that it discriminates coherent signals from noncoherent ones, and it is independent from the signal's energy, we calculate sum of the normalized projected energy per iteration as
as shown in (3). The amount of signal energy that is projected at each iteration depends on the signal structure. The signal with coherent structure needs less number of iterations, while noncoherent structured signals take more iterations to get decomposed. In order to calculate MP feature in a way that it discriminates coherent signals from noncoherent ones, and it is independent from the signal's energy, we calculate sum of the normalized projected energy per iteration as  . The MP feature for piano and aircraft signals is calculated as 2.9 and 10.6, respectively. As it is expected, MP feature is high for the noncoherent segment (aircraft), and low for the coherent segment (piano).
. The MP feature for piano and aircraft signals is calculated as 2.9 and 10.6, respectively. As it is expected, MP feature is high for the noncoherent segment (aircraft), and low for the coherent segment (piano).
Figure 15 demonstrates the feature vectors that are extracted from the aircraft (Figure 13(a)) and the piano signals (Figure 14(a)) in the feature domain. As it can be observed, the feature vectors from aircraft and piano are separate from each other in the feature space.
This figure represents the aircraft and piano segments in the feature plane. Since maximum three dimensions of the feature domain can be plotted, only three features of the feature vectors are shown in this figure. MOH, DH, and SW represent the second central moment of coefficient vectors in H, the derivative of coefficient vectors in H, and the sparsity of base vectors in W, respectively. As it can be observed from the feature domain, the feature vectors from aircraft and piano are separate from each other.
4.2.3. Pattern Classification
The pattern classification is to automatically group audio signals of same characteristics using the discriminatory features derived above. Similar to music classification, the Pattern classification was carried out by LDA-based classifier using the SPSS software [50].
4.2.4. Results and Discussion
The LDA classifier is trained using 75% signals in each group, and is tested on all the audio samples in the dataset. For each signal, 15 feature vectors are classified and the majority of the vote defines the class of that signal. Table 3 shows the classification accuracy. In this table, the first column contains the ten classes in the dataset and the number shows the number of signals in each class, for example, Aircraft includes 20 audio signals collected from different aircrafts. The number of correct and misclassified signals are shown in the next two columns and the accuracy percentage is presented in the last column. As it can be seen in Table 3, the overall classification accuracy of 85% is achieved. The classification rate is high for human speech (male and female), instruments (piano, drum and flute) and aircraft; however, the accuracy rate is lower in the cases of animal, bird and insect sounds. The reason is that these classes are created from a variety of creatures, for example, the animal class includes sounds of cow, elephant, hippo, hyena, wolf, sheep, horse, cat and donkey, which are very diverse in their nature.
In order to evaluate the relative performance of the proposed features, we compared them with the well-known MFCC features. MFCCs are short-term spectral features and are widely used in the area of audio and speech processing. In this paper, we computed the first 13 MFCCs for all the segments of the entire length of the audio signals and find the mean and variance of these 13 MFCCs as the MFCC features. For each audio signal we derived 26 features, 13 features were from the mean of the segment MFCCs and the remaining 13 were the variance of the segment MFCCs. These 26 features were computed for all the 192 signals and fed to an LDA-based classifier for classification. Using MFCC features, an overall classification accuracy of 75% was achieved which is 10% lower that the overall classification accuracy of our proposed features. Our experiments demonstrated that the proposed TF features are very effective in characterizing the nonstationary dynamics of the environmental audio signals, such as aircraft, helicopter, bird, insect, and music instruments.
Next, in order to obtain the role of each feature in the classification accuracy, we use the Students  -test to calculate the
-test to calculate the  value of the TF features and MFCC features extracted from each decomposed base and coefficient vectors. The feature with the smallest
value of the TF features and MFCC features extracted from each decomposed base and coefficient vectors. The feature with the smallest  value plays the most important role in the classification accuracy. Figure 16 demonstrates
value plays the most important role in the classification accuracy. Figure 16 demonstrates  as the relative importance of the 20 features. As shown in this figure, the MP feature plays the most significant role in the classification accuracy. It can also be observed that the proposed TF features show a higher significance compared to the fourth MFCC feature and higher. This is proven by comparing the accuracy results with the TF features (
as the relative importance of the 20 features. As shown in this figure, the MP feature plays the most significant role in the classification accuracy. It can also be observed that the proposed TF features show a higher significance compared to the fourth MFCC feature and higher. This is proven by comparing the accuracy results with the TF features ( ) and with the MFCC coefficients only (
) and with the MFCC coefficients only ( ).
).
In this section, we proposed a novel methodology to extract TF features for the purpose of environmental audio classification. Our methodology was proposed to address the tradeoff between long-term analysis of audio signals, and their non-stationarity characteristics. Experiments performed with a diverse database and the high-classification accuracies achieved by the proposed TFM decomposition feature extraction technique clearly demonstrated the potential of the technique as a true nonstationary tool in the form of a TFM decomposition approach for environmental audio classification.
5. Audio Fingerprinting and Watermarking
The technologies used for security of multimedia data include encryption, fingerprinting, and watermarking. Encryption can be used to package the content securely and force all accesses rules to the protected content. If the content is not packaged securely, the content could be easily copied. Encryption scrambles the content and renders the content unintelligible unless a decryption key is known. However, once an authorized user has decrypted the content, it does not provide any protection to the decrypted content. Encryption does not prevent an authorized user from making and distributing illegal copies. Watermarking and fingerprinting are two technologies that can provide protection to the data after it has been decrypted.
A watermark is a signal that is embedded in the content to produce a watermarked content. The watermark may contain information about the owner of the content and the access conditions of the content. When a watermark is added to the content, it introduces distortion. But the watermark is added in such a way that the watermarked content is perceptually similar to the original content. The embedded watermark may be extracted using a watermark detector. Since the watermark contains information that protects the content, the watermarking technique should be robust, that is, the watermark signal should be difficult to remove without causing significant distortion to the content.
In watermarking, the embedding process adds a watermark before the content is released. But watermarking cannot be used if the content has been already released. According to Venkatachalam et al. [57], there are about 0.5 trillion copies of sound recordings in existence and 20 billion sound recordings are added every year. This underscores the importance of securing legacy content. Fingerprinting is a technology to identify and protect legacy content. In multimedia fingerprinting, the main objective is to establish the perceptual equality of two multimedia objects: not by comparing the objects themselves, but by comparing the associated fingerprints. The fingerprints of a large number of multimedia objects, along with their associated metadata (e.g., name of artist, title, and album, copyright) are stored in a database. This database is usually maintained online and can be accessed by recording devices.
In recent years, the digital format has become the standard for the representation of multimedia content. Today's technology allows the copying and redistribution of multimedia content over the Internet at a very low or no cost. This has become a serious threat for multimedia content owners. Therefore, there is significant interest to protect copyright ownership of multimedia content (audio, image, and video). Watermarking is the process of embedding additional data into the host signal for identifying the copyright ownership. The embedded data characterizes the owner of the data and should be extracted to prove ownership. Besides copyright protection, watermarking may be used for data monitoring, fingerprinting, and observing content manipulations. All watermarking techniques should satisfy a set of requirements [58]. In particular, the embedded watermark should be:
-
(i)
imperceptible,
-
(ii)
undetectable to prevent unauthorized removal,
-
(iii)
resistant to all signal manipulations, and
-
(iv)
extractable to prove ownership.
Before the proposed technique is made public, all the above requirements should be met. In order to propose watermarking algorithms that are robust to signal manipulations, we introduced two TF signatures for audio watermarking: instantaneous mean frequency (IMF) of the signal, and fixed amplitude linear and quadratic phase signal (chirp). The following sections present an overview of the two proposed methods, and their performances.
5.1. IMF-Based Watermarking
We proposed a watermarking scheme using the estimated IMF of the audio signal. Our motivation for this work is to address two important features of security and imperceptibility and this can be achieved using spread spectrum and instantaneous mean frequency (IMF). In fact, the estimated IMF of the signal is examined as an optimal point of insertion of the watermark in order to maximize its energy while achieving imperceptibility.
5.1.1. Watermarking Algorithm
Figure 17 demonstrates the watermark embedding and extracting procedure. In this figure,  is a nonoverlapping block of the windowed signal. Based on Gabor's work on IF [1], Ville devised the Wigner-Ville Distribution (WVD), which showed the distribution of a signal over time and frequency. The IMF of a signal was then calculated as the first moment of the WVD with respect to frequency. In this work, instead of WVD, spectrogram was used which is free of cross terms and obtains a positive IMF. Therefore, the IMF of a signal could be expressed as [59]
is a nonoverlapping block of the windowed signal. Based on Gabor's work on IF [1], Ville devised the Wigner-Ville Distribution (WVD), which showed the distribution of a signal over time and frequency. The IMF of a signal was then calculated as the first moment of the WVD with respect to frequency. In this work, instead of WVD, spectrogram was used which is free of cross terms and obtains a positive IMF. Therefore, the IMF of a signal could be expressed as [59]

This IMF is computed over each time window of the spectrogram, and TFD  refers to the energy of the signal at a given time and frequency. Note that in (19),
refers to the energy of the signal at a given time and frequency. Note that in (19),  refers to the maximum frequency of the signal,
refers to the maximum frequency of the signal,  is the time index and
is the time index and  is the frequency index. From this we can derive an estimate of the IMF of a nonstationary signal assuming that the IMF is constant throughout the window. The watermark message is defined as a sequence of randomly generated bits that each bit is spread using a narrowband PN sequence, then shaped using BPSK modulation and an embedding strength. The modulated watermarked signal can now be defined by
is the frequency index. From this we can derive an estimate of the IMF of a nonstationary signal assuming that the IMF is constant throughout the window. The watermark message is defined as a sequence of randomly generated bits that each bit is spread using a narrowband PN sequence, then shaped using BPSK modulation and an embedding strength. The modulated watermarked signal can now be defined by

where  refers to the watermark or hidden message bit before spreading,
refers to the watermark or hidden message bit before spreading,  is the spreading code or the PN sequence which is low-passed by filter
is the spreading code or the PN sequence which is low-passed by filter  . The FIR low-pass filter should be chosen according to frequency characteristics of the audio signal; the cutoff frequency of the filter was chosen empirically to be 1.5 KHz.
. The FIR low-pass filter should be chosen according to frequency characteristics of the audio signal; the cutoff frequency of the filter was chosen empirically to be 1.5 KHz.  refers to the time-varying carrier frequency which represents the IMF of the audio signal. The power of the carrier signal is determined by
refers to the time-varying carrier frequency which represents the IMF of the audio signal. The power of the carrier signal is determined by  , and is adjusted according to the frequency masking properties of the HAS.
, and is adjusted according to the frequency masking properties of the HAS.
In order to understand the simultaneous masking phenomenon of the HAS, we will examine two different scenarios of simultaneous masking. First, in the case where a narrowband noise masks a simultaneously occurring tone within the same critical band, the signal-to-mask ratio is about 5 dB. Second, in the case of tone-masking noise, the noise needs to be about 24 dB below the masker excitation level. Meaning that, it is generally easier for a broadband noise to mask a tonal sound, than for the tonal sound to mask a broadband noise. Note that in both cases, the noise and tonal sounds need to occur within the same critical band for simultaneous masking to occur. In our case, the tone- or noise-like characteristic is determined for each window of the spectrogram and not for each component in the frequency domain. We found the entropy of the signal useful in determining whether the window can best be classified as tone-like or noise-like. The entropy can be expressed as

where

since the maximum entropy can be written as

We assume that if the entropy calculated is greater than half the maximum entropy, the window can be considered noise-like; otherwise it is tone-like. Based on these values, the watermark energy is then scaled by the coefficients  such that the watermark energy will be either 24 dB or 5 dB below that of the audio signal. In order to recover the watermark and thus the hidden message, the user needs to know the PN sequence and the IMF of the original signal. Figure 17 illustrates the message recovery operation. The decoding stage consists of a demodulation step using the IMF frequencies, and a dispreading step using the PN sequence.
such that the watermark energy will be either 24 dB or 5 dB below that of the audio signal. In order to recover the watermark and thus the hidden message, the user needs to know the PN sequence and the IMF of the original signal. Figure 17 illustrates the message recovery operation. The decoding stage consists of a demodulation step using the IMF frequencies, and a dispreading step using the PN sequence.
5.1.2. Algorithm Performance
The proposed watermarking algorithm was applied to several different music files ranging between classical, pop, rock, and country music. These files were sampled at a rate of 44.1 kHz, and 25 bits were embedded into a 5 sec sample of the audio signal. Figure 18 gives an overview of the watermark procedure for a voiced pop segment. As can be seen from these plots, the watermark envelope follows the shape of the music signal. As a result, the strength of the watermark increases as the amplitude of the audio signal increases.
Overview of watermarking procedure for POP voiced segment ("viorg. wav"). Several robustness tests based on StirMark Benchmark [60] attacks were performed on the five different audio files to examine the reliability of our algorithm against signal manipulations. In an attempt to standardize this, Petitcolas et al. [60] realized that many claims of robustness have been made in several papers without following the same criteria. They have published a work with 4 popular audio watermarking algorithms, three of which were submitted by companies have been exposed to several attacks. The algorithms are referred to as A, B, C, and D. The summary of these results can be seen in Table 4. For each algorithm, 6 audio segments were watermarked and it was noted whether the watermark was completely destroyed or somewhat changed by the attacks. As can be seen from the above tests, our technique offers several improvements over existing algorithms.
As it was demonstrated in this section, the proposed IMF-based watermarking is a robust watermarking method. In the following section, the proposed chirp-based watermarking technique is introduced that uses linear chirps as watermarking message. The motivation of using linear chirps as a TF signature is taking the advantage of using a chirp detector in the final stage of watermark decoding to improve the robustness of the watermarking technique and also to decrease the complexity of the watermark detection stage compared to the IMF-based watermarking.
5.2. Chirp-Based Watermarking
We proposed a chirp-based watermarking scheme [61], where a linear frequency modulated signal, known as a chirp, is embedded as the watermark message. Our motivation in chirp-based watermarking is utilizing a chirp detection tool in the postprocessing stage to compensate bit errors that occur in embedding and extracting the watermark signal. Some recent TF-based watermarking studies include the work in [62, 63].
5.2.1. Watermark Algorithm
Figure 19 provides an overview of the chirp-based watermarking scheme for a spread spectrum watermarking algorithm. The watermark message is a 1-bit quantized amplitude version of the normalized chirp  on a TF plane, with initial and final frequencies
on a TF plane, with initial and final frequencies  and
and  , respectively. Each watermark bit is spread with a secret-key generated binary PN sequence
, respectively. Each watermark bit is spread with a secret-key generated binary PN sequence  . The spread spectrum signal
. The spread spectrum signal  appears as wideband noise and occupies the entire frequency spectrum spanned by the audio signal
appears as wideband noise and occupies the entire frequency spectrum spanned by the audio signal  . In order for the embedded watermark to be imperceptible, the watermark signal is perceptually shaped by a scale factor
. In order for the embedded watermark to be imperceptible, the watermark signal is perceptually shaped by a scale factor  , and a low-pass filter. The cutoff frequency of the low-pass filter is
, and a low-pass filter. The cutoff frequency of the low-pass filter is  , where
, where  is the sampling frequency of the audio signal. The low-pass filtering step allows us to increase the value of
is the sampling frequency of the audio signal. The low-pass filtering step allows us to increase the value of  to a value while maintaining imperceptibility. We used the empirically determined value of 0.3 for the embedding strength parameter
to a value while maintaining imperceptibility. We used the empirically determined value of 0.3 for the embedding strength parameter  .
.
Since the watermark bit is embedded in the low-frequency bands of the transmitted signal, we extract the watermark bit by processing the low-frequency bands of the received signal, and despread the signal using the same PN sequence used in watermark embedding. We repeat the bit estimation process outlined above for each input block, until we have an estimate of all the transmitted watermark bits. While it is possible to combine the estimated bits sequence, we can improve the performance of the watermark extraction algorithm by postprocessing the estimated bits. Here, as we know that the embedded watermark has a chirp structure, by using a chirp detector, the original watermark message can be estimated.
5.2.2. Postprocessing of the Estimated Bits for Watermark Message Extraction
After all watermark bits are extracted, we first construct the TFD of the extracted watermark. The TF representation resulting from the TFD of the estimated bits can be considered as an image in TF plane. Once we generate the image of the TF plane, a parametric line detection algorithm based on the Hough-Radon transform (HRT) operates searches for the presence of the straight line and estimates its parameters. The HRT is a parametric tool to detect the pixels that belong to a parametric constraint of either a line or curve in a gray-level image [64]. HRT divides the Hough-Radon parameter space into cells, and then calculates the accumulator value for each cell in the parameter space. The cell with the highest accumulator value represents the parameter of the HRT constraint. Since we are looking for the embedded chirp as straight lines in the TF plane in the application of postprocessing of chirp-based watermarking, we can apply the HRT method to detect the embedded chirp. First, the extracted watermark bits are transformed to the TF plane; then the HRT detects the line representing the chirp in TFD. In order to achieve a good detection performance, Wigner-Ville Transform (WV) is used as the TFD representation of the signal as it provides fine TF resolution.
5.2.3. Technique Evaluation
We implemented the time-domain spread spectrum watermarking algorithm to embed and extract watermark. The sampling frequency  to generate the watermark signals. Therefore, the initial and final frequencies,
to generate the watermark signals. Therefore, the initial and final frequencies,  and
and  of the linear chirps representing all watermark messages are constrained to
of the linear chirps representing all watermark messages are constrained to  . As host signals, we used five different audio files with
. As host signals, we used five different audio files with  and 16 bits/sample quantization. These sample audio files represent rock, classical, harp, piano, and pop music, respectively. We embedded watermark messages into audio signals of 40 second duration for a chip length of 10,000 samples per watermark bit (corresponding to an embedding rate of 4.41 bps), and into audio signals of 20 second duration for a chip length of 5,000 samples per watermark bit (corresponding to an embedding rate of 8.82 bps). In both cases, these values result in 176-bit long chirp sequences.
and 16 bits/sample quantization. These sample audio files represent rock, classical, harp, piano, and pop music, respectively. We embedded watermark messages into audio signals of 40 second duration for a chip length of 10,000 samples per watermark bit (corresponding to an embedding rate of 4.41 bps), and into audio signals of 20 second duration for a chip length of 5,000 samples per watermark bit (corresponding to an embedding rate of 8.82 bps). In both cases, these values result in 176-bit long chirp sequences.
To measure the robustness of the watermarking algorithm, we performed 8 signal manipulation tests, which represent commonly used signal processing techniques. Table 2 shows the BER results expressed as a percentage of the total number of watermark bits for the two chip lengths and for each signal manipulation operation.
In all the robustness tests performed, the HRT was able to extract the watermark message parameters correctly even in the worst-case scenario. The experiments showed that the HRT-based postprocessing is able to estimate the correct watermark message up to a BER of 20%, where the maximum BER reported in Table 5 was about 6%. The proposed chirp-based watermarking using HRT as postprocessing step offers a robust watermark extraction performance; however, calculation of WVD and taking HRT on the resulted WVD has a high complexity of maximum  , where
, where  is the length of the chirp. In order to decrease the complexity of the postprocessing stage, we could use Discrete Polynomial Phase Transform (DPPT) [65] as a faster chirp estimator to estimate the watermark message. DPPT is a parametric signal analysis approach for estimating the phase parameters of constant amplitude polynomial phase signals. The DPPT operates directly on the signal in time domain and is a computationally efficient method comparing to HRT. Complexity of DPPT is
is the length of the chirp. In order to decrease the complexity of the postprocessing stage, we could use Discrete Polynomial Phase Transform (DPPT) [65] as a faster chirp estimator to estimate the watermark message. DPPT is a parametric signal analysis approach for estimating the phase parameters of constant amplitude polynomial phase signals. The DPPT operates directly on the signal in time domain and is a computationally efficient method comparing to HRT. Complexity of DPPT is  .
.
The proposed chirp-based watermark representation is fundamentally generic and inherently flexible for embedding and extraction purposes such that it can be embedded and extracted in any domain. Accordingly, we can embed the chirp sequence into the audio or image signals using any of the methods in [66, 67]. For example, if we were to use the algorithm developed in [68] we would embed the chirp sequence into the Fourier coefficients. At the receiver, we extract the chirp sequence which is likely to have some bits in error. We then input the extracted chirp sequence to the HRT- or DPPT-based postprocessing stage to detect the slope of the chirp.
Table 6 presents the result of the chirp-based watermarking using DPPT for Images in Discrete Cosine Transform domain (DCT) [69]. As it is observed in this table, the robustness of the watermarking scheme is satisfactory.
Although the proposed chirp-based watermarking representation is not a classical forward error correction (FEC) code, an analogy can be made between FEC codes and this new representation as they both introduce performance improvements at the expense of code redundancy. FEC codes have been commonly used in watermarking to reduce the bit error rate (BER) in order to achieve the desired BER performance. Most commonly used FEC codes for audio watermarking are Bose-Chaudhuri-Hocquenghem (BCH) codes and repetition codes. Table 6 compares the performance of the chirp-based watermarking using DPPT chirp detector, Repetition coding and BCH coding; all codes have a redundancy value of about 11/12. The chirp-based watermarking offers higher amount of BER correction than the Repetition and BCH coding.
6. Summary
In this paper we presented a stage-by-stage implementation and analysis of three important audio processing tasks, namely,  audio compression,
audio compression,  audio classification, and
audio classification, and  securing audio content using TF approaches. The proposed TF methodologies are best suited for analyzing highly nonstationary audio signals. Although the audio compression results were not on par with the state-of-the-art coders, we introduced a novel way of performing audio compression. Moreover, the proposed coder is not as refined as the state-of-the-art commercial coders, which to some extent explains its poor performance. A content-based audio retrieval application was presented to explain the basic blocks of audio classification. TF features were extracted from the music signals and were segregated into 6 groups using a pattern classifier. High-classification accuracies of >90% (cross validated) were reported. We proposed a novel methodology to extract TF features for the purpose of environmental audio classification, and called the developed technique, TFM decomposition feature extraction. The obtained features from ten different environmental audio signals were fed into a multiclassifier, and a classification accuracy of 85% was achieved, which was 10% higher than the classical features.
securing audio content using TF approaches. The proposed TF methodologies are best suited for analyzing highly nonstationary audio signals. Although the audio compression results were not on par with the state-of-the-art coders, we introduced a novel way of performing audio compression. Moreover, the proposed coder is not as refined as the state-of-the-art commercial coders, which to some extent explains its poor performance. A content-based audio retrieval application was presented to explain the basic blocks of audio classification. TF features were extracted from the music signals and were segregated into 6 groups using a pattern classifier. High-classification accuracies of >90% (cross validated) were reported. We proposed a novel methodology to extract TF features for the purpose of environmental audio classification, and called the developed technique, TFM decomposition feature extraction. The obtained features from ten different environmental audio signals were fed into a multiclassifier, and a classification accuracy of 85% was achieved, which was 10% higher than the classical features.
Furthermore, we brought highlights of our proposed watermarking schemes by introducing two TF signatures. We used IMF estimation of the signal, nonlinear TF signature, as the watermark signal. Due to complexity of the watermark estimation, then we proposed chirp-based watermarking, in which we embedded the linear phase signals as TF signatures. HRT is used as chirp detector in the postprocessing stage to compensate the BERs in the estimated watermark signal. The method could correct the error up to BER of 20%, and the robustness result was satisfactory. Since the HRT had high complexity, and the postprocessing stage was time consuming, we used DPPT instead of HRT in postprocessing. The DPPT-based postprocessing was applied on chirp-based image watermarking. Due to error correction property of the chirp-based watermarking, we also compared it with two well-known FEC schemes; it was shown that the chirp-based watermarking offered higher BER correction than the Repetition, and BCH coding.
References
Mallat S: A Wavelet Tour of Signal Processing. Academic Press, New York, NY, USA; 1998.
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397-3415. 10.1109/78.258082
Cohen L: Time-frequency distributions—a review. Proceedings of the IEEE 1989, 77(7):941-981. 10.1109/5.30749
Gribonval R, IRISA-INRIA Rennes: Fast matching pursuit with a multiscale dictionary of Gaussian chirps. IEEE Transactions on Signal Processing 2001, 49(5):994-1001. 10.1109/78.917803
Choi H, Williams WJ: Improved time-frequency representation of multicomponent signals using exponential kernels. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(6):862-871. 10.1109/ASSP.1989.28057
Daubechies I: Wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory 1990, 36(5):961-1005. 10.1109/18.57199
Peng ZK, Tse PW, Chu FL: An improved Hilbert-Huang transform and its application in vibration signal analysis. Journal of Sound and Vibration 2005, 286(1-2):187-205. 10.1016/j.jsv.2004.10.005
Cohen L, Posch TE: Positive time-frequency distribution functions. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985, 33(1):31-38. 10.1109/TASSP.1985.1164512
Deshpande H, Singh R, Nam U: Classification of music signals in the visual domain. Proceedings of the COSTG6 Conference on Digital Audio Effects, 2001
Tacer B, Loughlin P: Time-frequency-based classification. Advanced Signal Processing Algorithms, Architectures, and Implementations VI, August 1996, Denver, Colo, USA, Proceedings of SPIE 2846: 186-192.
Paraskevas I, Chilton E: Audio classification using acoustic images for retrieval from multimedia databases. Proceedings of the 4th EURASIP Conference focused on Video/Image Processing and Multimedia Communications, July 2003 1: 187-192.
Esmaili S, Krishnan S, Raahemifar K: Content based audio classification and retrieval using joint time-frequency analysis. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, May 2004, can V-665-V-668.
Wan B, Plumbley MD: Musical audio stream separation by non-negative matrix factorization. Proceedings of the Digital Music Research Network Summer Conference (DMRN '05), 2005, Glasgow, UK
Smaragdis P: Non-negative matrix factor deconvolution; extraction of multiple sound sources from monophonic inputs. Proceedings of the 5th International Conference on Independent Component Analysis and Blind Signal Separation (ICA '04), September 2004, Granada, Spain, Lecture Notes in Computer Science 3195: 494-499.
Holzapfel A, Stylianou Y: Musical genre classification using nonnegative matrix factorization-based features. IEEE Transactions on Audio, Speech and Language Processing 2008, 16(2):424-434.
Krishnan S, Ghoraani B: A joint time-frequency and matrix decomposition feature extraction methodology for pathological voice classification. EURASIP Journal on Advances in Signal Processing 2009, 2009:-11.
Shams N, Ghoraani B, Krishnan S: Audio feature clustering for hearing aid systems. Proceedings of IEEE Toronto International Conference: Science and Technology for Humanity (TIC-STH '09), September 2009 976-980.
Ghoraani B, Krishnan S: Quantification and localization of features in time-frequency plane. Proceedings of IEEE Canadian Conference on Electrical and Computer Engineering (CCECE '08), May 2008 1207-1210.
Groutage D, Bennink D: Feature sets for nonstationary signals derived from moments of the singular value decomposition of cohen-posch (positive time-frequency) distributions. IEEE Transactions on Signal Processing 2000, 48(5):1498-1503. 10.1109/78.840002
Lee D, Seung H: Algorithms for non-negative matrix factorization. Advances in Neural Information Processing Systems 13, 2000 556-562.
Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ: Algorithms and applications for approximate nonnegative matrix factorization. Computational Statistics and Data Analysis 2007, 52(1):155-173. 10.1016/j.csda.2006.11.006
Buciu I: Non-negative matrix factorization, a new tool for feature extraction: theory and applications. International Journal of Computers, Communications and Control 2008, 3: 67-74.
Lin C-J: Projected gradient methods for nonnegative matrix factorization. Neural Computation 2007, 19(10):2756-2779. 10.1162/neco.2007.19.10.2756
Painter T, Spanias A: Perceptual coding of digital audio. Proceedings of the IEEE 2000, 88(4):451-512. 10.1109/5.842996
Umapathy K, Krishnan S: Perceptual coding of audio signals using adaptive time-frequency transform. EURASIP Journal on Audio, Speech and Music Processing 2007, 2007:-14.
Umapathy K, Krishnan S: Audio Coding and Classification: Principles and Algorithms in Mobile Multimedia Broadcasting Multi-Standards. Springer, San Diego, Calif, USA; 2009.
Brandenburg K, Bosi M: MPEG-2 advanced audio coding: overview and applications. Proceedings of the 103rd Audio Engineering Society Convention, 1997, New York, NY, USA Preprint 4641
Eberlein E, Popp H: Layer-3, a flexible coding standard. Proceedings of the 94th Audio Engineering Society Convention, March 1993, Berlin, Germany Preprint 3493
Herre J: Second generation iso/mpeg audio layer-3 coding. Proceedings of the 98th Audio Engineering Society Convention, February 1995, Paris, France
JTC1/SC29/WG11 I: Overview of the mpeg-4 standard. International Organisation for Standardisation, March 2002
Meltzer S, Moser G: MPEG-4 HE-AAC v2—audio coding for today's digital media world. EBU Technical Review 2006, (305):37-48.
Orfanidis SJ: Introduction to Signal Processing. Prentice-Hall, New Jersey, NJ, USA; 1996.
Ryden T: Using listening tests to assess audio codecs. In Collected Papers on Digital Audio Bit-Rate Reduction. AES; 1996:115-125.
Goodwin MM: Adaptive Signal Models: Theory, Algorithms and Audio Applications. Kluwer Academic Publishers, Norwell, Mass, USA; 1998.
Krstulović S, Gribonval R: MPTK: matching pursuit made tractable. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006 3: 496-499.
Campbell JP Jr.: Speaker recognition: a tutorial. Proceedings of the IEEE 1997, 85(9):1437-1462. 10.1109/5.628714
Lu L, Zhang H-J, Jiang H: Content analysis for audio classification and segmentation. IEEE Transactions on Speech and Audio Processing 2002, 10(7):504-516. 10.1109/TSA.2002.804546
Umapathy K, Krishnan S, Jimaa S: Multigroup classification of audio signals using time-frequency parameters. IEEE Transactions on Multimedia 2005, 7(2):308-315.
Guo G, Li SZ: Content-based audio classification and retrieval by support vector machines. IEEE Transactions on Neural Networks 2003, 14(1):209-215. 10.1109/TNN.2002.806626
Tzanetakis G, Cook P: Musical genre classification of audio signals. IEEE Transactions on Speech and Audio Processing 2002, 10(5):293-302. 10.1109/TSA.2002.800560
Burges CJC, Platt JC, Jana S: Distortion discriminant analysis for audio fingerprinting. IEEE Transactions on Speech and Audio Processing 2003, 11(3):165-174. 10.1109/TSA.2003.811538
Dugelay J-L, Junqua J-C, Kotropoulos C, Kuhn R, Perronnin F, Pitas I: Recent advances in biometric person authentication. Proceedings of IEEE International Conference on Acoustic, Speech, and Signal Processing, May 2002 4: 4060-4063.
Cooper M, Foote J: Summarizing popular music via structural similarity analysis. Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, 2003 127-130.
Xu C, Maddage NC, Shao X: Automatic music classification and summarization. IEEE Transactions on Speech and Audio Processing 2005, 13(3):441-450.
Kim H-G, Moreau N, Sikora T: Audio classification based on MPEG-7 spectral basis representations. IEEE Transactions on Circuits and Systems for Video Technology 2004, 14(5):716-725. 10.1109/TCSVT.2004.826766
Soltau H, Schultz T, Westphal M, Waibel A: Recognition of music type. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, May 1998 1137-1140.
Moore BCJ: An Introduction to the Psychology of Hearing. Academic Press, Toronto, Canada; 1992.
Allamanche E, Herre J, Hellmuth O, Froba B, Kastner T, Cremer M: Content-based identification of audio material using MPEG-7 low level description. Proceedings of the 2nd Annual International Symposium on Music Information Retrieval, October 2001 197-204.
SPSS Inc : SPSS advanced statistics user's guide. In User Manual. SPSS Inc., Chicago, Ill, USA; 1990.
Fukunaga K: Introduction to Statistical Pattern Recognition. Academic Press, San Diego, Calif, USA; 1990.
Panagiotakis C, Tziritas G: A speech/music discriminator based on RMS and zero-crossings. IEEE Transactions on Multimedia 2005, 7(1):155-166.
Microsoft http://research.microsoft.com/
Freeman G, Dony R, Areibi S: Audio environment classification for hearing aids using artificial neural networks with windowed input. Proceedings of IEEE Symposium on Computational Intelligence in Image and Signal Processing, April 2007, Honolulu, Hawaii 183-188.
Chu S, Narayanan S, Kuo C-CJ: Environmental sound recognition using MP-based features. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), March-April 2008 1-4.
Hoyer PO: Non-negative matrix factorization with sparseness constraints. Journal of Machine Learning Research 2004, 5: 1457-1469.
Venkatachalam V, Cazzanti L, Dhillon N, Wells M: Automatic identification of sound recordings. IEEE Signal Processing Magazine 2004, 21(2):92-99. 10.1109/MSP.2004.1276117
Arnold M: Audio watermarking: features, applications and algorithms. Proceedings of IEEE International Conference on Multimedia and Expo (ICME '00), August 2000 1013-1016.
Krishnan S: Instantaneous mean frequency estimation using adaptive time-frequency distributions. Proceedings of the Canadian Conference on Electrical and Computer Engineering, May 2001 141-146.
Petitcolas AP, et al.: Stirmark benchmark: audio watermarking attacks. Proceedings of the International Conference on Information Technology: Coding and Computing (ITCC '01), April 2001 49-55.
Erküçük S, Krishnan S, Zeytinoǧlu M: A robust audio watermark representation based on linear chirps. IEEE Transactions on Multimedia 2006, 8(5):925-936.
Stanković S, Orović I, Žarić N: Robust speech watermarking procedure in the time-frequency domain. EURASIP Journal on Advances in Signal Processing 2008, 2008:-9.
Stanković S, Orović I, Žarić N: An application of multidimensional time-frequency analysis as a base for the unified watermarking approach. IEEE Transactions on Image Processing 2010, 19(3):736-745.
Rangayyan R, Krishnan S: Feature identification in the time-frequency plane by using the hough-radon transform. IEEE Transactions on Pattern Recognition 2001, 34: 1147-1158. 10.1016/S0031-3203(00)00073-X
Lam L, Krishnan S, Ghoraani B: Discrete polynomial transform for digital image watermarking application. Proceedings of IEEE International Conference on Multimedia and Expo (ICME '06), July 2006 1569-1572.
Lie W-N, Chang L-C: Robust and high-quality time-domain audio watermarking subject to psychoacoustic masking. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '01), May 2001 45-48.
Swanson MD, Zhu B, Tewfik AH: Current state of the art, challenges and future directions for audio watermarking. Proceedings of the 6th International Conference on Multimedia Computing and Systems, June 1999 1: 19-24.
Seok JW, Hong JW: Audio watermarking for copyright protection of digital audio data. Electronics Letters 2001, 37(1):60-61. 10.1049/el:20010029
Ghoraani B, Krishnan S: Chirp-based image watermarking as error-control coding. Proceedings of the International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP '06), December 2006 647-650.
Pereira S, Voloshynovskiy S, Madueno M, Marchand-Maillet S, Pun T: Second generation benchmarking and application oriented evaluation. Proceedings of the Information Hiding Workshop III, April 2001, Pittsburgh, Pa, USA
Umapathy K, Krishnan S, Rao RK: Audio signal feature extraction and classification using local discriminant bases. IEEE Transactions on Audio, Speech and Language Processing 2007, 15(4):1236-1246.
Esmaili S, Krishnan S, Raahemifar K: Audio watermarking using time-frequency characteristics. Canadian Journal of Electrical and Computer Engineering 2003, 28(2):57-61. 10.1109/CJECE.2003.1532509
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Umapathy, K., Ghoraani, B. & Krishnan, S. Audio Signal Processing Using Time-Frequency Approaches: Coding, Classification, Fingerprinting, and Watermarking. EURASIP J. Adv. Signal Process. 2010, 451695 (2010). https://doi.org/10.1155/2010/451695
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/451695




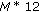 bits.
bits.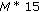 bits.
bits.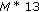 bits.
bits.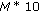 bits.
bits.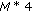 bits.
bits.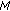 iterations for a 5 s duration of the signal is
iterations for a 5 s duration of the signal is 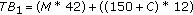 , where
, where  is the number of curve fitted points, and
is the number of curve fitted points, and 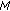 is the number of perceptually important functions.
is the number of perceptually important functions.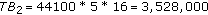 .
.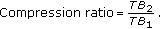
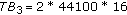 .
. .
. .
.













