- Research Article
- Open access
- Published:
Automatic Modulation Recognition Using Wavelet Transform and Neural Networks in Wireless Systems
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 532898 (2010)
Abstract
Modulation type is one of the most important characteristics used in signal waveform identification. In this paper, an algorithm for automatic digital modulation recognition is proposed. The proposed algorithm is verified using higher-order statistical moments (HOM) of continuous wavelet transform (CWT) as a features set. A multilayer feed-forward neural network trained with resilient backpropagation learning algorithm is proposed as a classifier. The purpose is to discriminate among different M-ary shift keying modulation schemes and the modulation order without any priori signal information. Pre-processing and features subset selection using principal component analysis is used to reduce the network complexity and to improve the classifier's performance. The proposed algorithm is evaluated through confusion matrix and false recognition probability. The proposed classifier is shown to be capable of recognizing the modulation scheme with high accuracy over wide signal-to-noise ratio (SNR) range over both additive white Gaussian noise (AWGN) and different fading channels.
1. Introduction
Blind signal interception applications have a great importance in the domain of wireless communications. Developing more effective automatic digital modulation recognition (ADMR) algorithms is an essential step in the interception process. These algorithms yield to an automatic classifier of the different waveforms and modulation schemes used in telecommunication systems (2G/3G and 4G).
In particular, ADMR has gained a great attention in military applications, such as communication intelligence (COMINT), electronic support measures (ESM), spectrum surveillance, threat evaluation, and interference identification. Also recent and rapid developments in software-defined radio (SDR) have given ADMR more importance in civil applications, since the flexibility of SDR is based on perfect recognition of the modulation scheme of the desired signal.
Modulation classifiers are generally divided into two categories. The first category is based on decision-theoretic approach while the second on pattern recognition [1]. The decision-theoretic approach is a probabilistic solution based on a priori knowledge of probability functions and certain hypotheses [2, 3]. On the other hand, the pattern recognition approach is based on extracting some basic characteristics of the signal called features [4–12]. This approach is generally divided into two subsystems: the features extraction subsystem and the classifier subsystem [6]. However, the second approach is more robust and easier to implement if the proper features set is chosen.
In the past, much work has been conducted on modulation identification. The identification techniques, which had been employed to extract the signal features necessary for digital modulation recognition, include spectral-based feature set [7], higher order cumulants (HOC) [8, 9], constellation shape [10], and wavelets transforms [11, 12]. With their efficient performance in pattern recognition problems (e.g., modulation classification), many studies have proposed the application of artificial neural networks (ANNs) as classifiers [4–7].
In [13], Hong and Ho studied the use of wavelet transform to distinguish among QAM, PSK, and FSK signals. In their work, they have used a wavelet transform to extract the transient characteristics in a digital modulated signal. It has been shown that when the signal-to-noise ratio (SNR) is greater than 5 dB, the percentage of correct identification is about 97%.
In [6], Wong and Nandi have proposed a method for ADMR using artificial neural networks and genetic algorithms. In their study, they have presented the use of resilient backpropagation (RPROP) as a training algorithm for multi-layer perception (MLP) recogniser. The genetic algorithm is used in [6] to select the best feature subset from the combined statistical and spectral features set. This method requires carrier frequency estimation, channel estimation, and perfect phase recovery process.
Using the statistical moments of the probability density function (PDF) of the phase, the authors in [14] have investigated the problem of modulation recognition in PSK-based systems. It is shown that the n th moment (n even) of the signal's phase is a monotonically increasing function of the modulation order. On the basis of this property, the study in [14] formulates a general hypothesis testing problem to develop a decision rule and to derive an analytical expression for the probability of misclassification. Similarly, El-Mahdy and Namazi [15] developed and analyzed different classifiers for M-ary frequency shift keying (M-FSK) signals over a frequency nonselective Rayleigh fading channel. The classifier in [15] employs an approximation of the likelihood function of the frequency-modulated signals for both synchronous and asynchronous waveforms. Employing adaptive techniques, Liedtke [16] proposed an adaptive procedure for automatic modulation recognition of radio signals with a priori unknown parameters. The results of modulation recognition are important in the context of radio monitoring or electronic support measurements. A digital modulation classification method based on discrete wavelet transform and ANNs was presented in [17]. In this paper, an error backpropagation learning with momentum is used to speed up the training process and improve the convergence of the ANN. This method was developed in [18] by combining adaptive resonance theory 2A (ART2A) with discrete wavelet neural network. It was shown through simulations that high recognition capability can be achieved for modulated signals corrupted with Gaussian noise at 8 dB SNR. Three different automatic modulation recognition algorithms have been investigated and compared in [19]. The first is based on the observation of the amplitude histograms, the second on the continuous wavelet transform and the third on the maximum likelihood for the joint probability densities of phases and amplitudes.
In [20], Pedzisz and Mansour derived and analyzed a new pattern recognition approach for automatic modulation recognition of M-PSK signals in broadband Gaussian noise. This method is based on constellation rotation of the received symbols and fourth-order cumulants of the in-phase distribution of the desired signal. In [21], the recognition vector of the decision-theoretic approach and that of the cumulant-based classification are combined to compose a higher dimension hyperspace to get the benefits of both methods. The composed vector is applied to a radial basis function (RBF) neural network, yielding to more reasonable reference points. The method proposed in [21] was shown to cover large number of modulation schemes in AWGN channels even under low SNR. In [22], Tadaion et al. have derived a generalized likelihood ratio test (GLRT), where they have suggested a computationally efficient implementation thereof. Using discrete wavelet decompositions and adaptive network-based fuzzy inference system, a comparative study of implementation of feature extraction and classification algorithms was presented in [23].
Also in [24], Su et al. described a likelihood test-based modulation classification method for identifying the modulation scheme of SDR in real-time without pilot transmission. Unlike prior works, the study in [24] converts an unknown signal symbol to an address of a look-up table where it loads the precalculated values of the test functions for the likelihood ratio test to produce the estimated modulation scheme in real-time.
In this paper we focus on the continuous wavelet transform (CWT) to extract the classification features. One of the reasons for this choice is due to the capability of the transform to precisely introduce the properties of the signal in time and frequency [25]. The extracted features are higher order statistical moments (HOM) of the continuous wavelet transform. Our proposed classifier is a multi-layer feed-forward neural network trained using the resilient backpropagation learning algorithm (RPROP). Principal component analysis-(PCA-) based features selection is used to select the best subset from the combined HOM features subsets. This classifier has the capability of recognizing the M-ary amplitude shift keying (M-ASK), M-ary frequency shift keying (M-FSK), minimum shift keying (MSK), M-ary phase shift keying (M-PSK), and M-ary quadratic amplitude modulation (M-QAM) signals and the order of the identified modulation. The performance of the proposed algorithm is examined based on the confusion matrix and false recognition probability (FRP). The AWGN channel is considered when developing the mathematical model and through most of the results. Some additional simulations are carried to examine the performance of our algorithm over several fading channel models to assess the performance of our algorithm in a more realistic channel.
The remainder of the paper is organized as follows. Section 2 defines the mathematical model of the proposed problem and presents CWT calculations of different considered digitally modulated signals. Section 3 describes the process of feature extraction using the continuous wavelet transform. Section 4 focuses on features set pre-processing and subset selection, besides the structure of the artificial neural network and the learning algorithm. The results, algorithm performance analysis, and a comparative study with some existing recognition algorithms are presented in Section 5. Conclusions and perspectives of the research work are presented in Section 6.
2. Mathematical Model
In this study, the properties of the continuous wavelet transform are used to extract the necessary features for modulation recognition. The main reason for this choice is due to the capability of this transform to locate, in time and frequency, the instantaneous characteristics of a signal. More simply, the wavelet transform has the special feature of multiresolution analysis (MRA). In the same manner as Fourier transform can be defined as being a projection on the basis of complex exponentials, the wavelet transform is introduced as projection of the signal on the basis of scaled and time-shifted versions of the original wavelet (so-called mother wavelet) in order to study its local characteristics [25]. The importance of wavelet analysis is its scale-time view of a signal which is different from the time-frequency view and leads to MRA.
The continuous wavelet transform of a received signal  is defined as [25]
is defined as [25]

where  is the scale variable,
is the scale variable,  is the translation variable, and * denotes complex conjugate. This defines the so-called
is the translation variable, and * denotes complex conjugate. This defines the so-called  , where
, where  define the wavelet transform coefficients. The Haar wavelet is chosen as the mother wavelet where it is given by [25]
define the wavelet transform coefficients. The Haar wavelet is chosen as the mother wavelet where it is given by [25]

The main purpose of the mother wavelet is to provide a source function to generate  , which are simply the translated and scaled versions of the mother wavelet, known as baby wavelets, as follows [25]:
, which are simply the translated and scaled versions of the mother wavelet, known as baby wavelets, as follows [25]:

Let the received waveform  ,
,  be described as
be described as

where  is the symbol duration and channel is the channel function which includes the channel effect on the signal. For additive white Gaussian noise (AWGN) channel, the received waveform is described as
is the symbol duration and channel is the channel function which includes the channel effect on the signal. For additive white Gaussian noise (AWGN) channel, the received waveform is described as

where  is a complex additive white Gaussian noise.
is a complex additive white Gaussian noise.
The signal  can be presented as [13]
can be presented as [13]

where  is the carrier frequency,
is the carrier frequency,  is the carrier initial phase, and
is the carrier initial phase, and  is the baseband complex envelope of the signal
is the baseband complex envelope of the signal  , defined by
, defined by

with  being the number of observed symbols,
being the number of observed symbols,  is the pulse shaping function of duration
is the pulse shaping function of duration  ,
,  is the average signal power, and
is the average signal power, and  is the complex amplitude.
is the complex amplitude.
In our work we will focus on different M-ary shift keying modulated signals digitalized in RF or IF stages (the carrier frequency is unknown) with respect to SDR principles. That is, it is essential to know that the recognition is done without any priori signal information.
Presenting and calculating the wavelet transform of digitally modulated signals using different modulation schemes will clarify the role of wavelet analysis in feature extraction procedure. The wavelet analysis concept will be studied using only one family of wavelets (Haar wavelet). All the results and figures of CWT presented in this section are obtained using the Haar wavelet. Nevertheless, in our simulations we will extend our results to other families including Daubechies, Morlet, Meyer, Symlet, and Coiflet.
By extending the work of Hong and Ho [13], from (1)–(3), (6), and (7), the magnitude of continuous wavelet transform is given by

where  is the amplitude of the i th symbol.
is the amplitude of the i th symbol.
The normalized signal is defined as follows:

In what follows, the continuous wavelet transform of the normalized signal will be taken into consideration. Knowing that the amplitude of the normalized signal is constant and from (8), it is clear that the signal normalization will only affect the wavelet transform of nonconstant envelope modulations (i.e., ASK and QAM), and will not affect wavelet transform of constant envelope ones (i.e., FSK, MSK, and PSK). Note that there will be distinct peaks in the wavelet transform of the signal and that of the normalized one resulting from phase changes at the times where the Haar wavelet covers a symbol change. In what follows, we consider the magnitude of the wavelet transforms for different modulation schemes.
Given the complex envelope of QAM signal

where  are the assigned QAM symbols, the corresponding wavelet transform is given by
are the assigned QAM symbols, the corresponding wavelet transform is given by

It is clear from (11) that for a certain scale value, the  is a multi-step function. Considering the normalized QAM signal:
is a multi-step function. Considering the normalized QAM signal:

The  is constant since the signal loses its amplitude information. Figure 1 shows the multi-step CWT magnitude of 64-QAM signal and the constant CWT magnitude of normalized 64-QAM signal (as a function of
is constant since the signal loses its amplitude information. Figure 1 shows the multi-step CWT magnitude of 64-QAM signal and the constant CWT magnitude of normalized 64-QAM signal (as a function of  the translation sampling index).
the translation sampling index).
Let us consider the complex envelope of ASK signal

where  . From (8), the wavelet transform of ASK signal is given by
. From (8), the wavelet transform of ASK signal is given by

It is clear from (14) that for a certain scale, the  of ASK signal is a multi-step function since the amplitude
of ASK signal is a multi-step function since the amplitude  is a variable. As for the normalized ASK signals
is a variable. As for the normalized ASK signals

and its corresponding  is constant. Figure 2 shows CWT magnitude of both 16-ASK signal and its normalized version.
is constant. Figure 2 shows CWT magnitude of both 16-ASK signal and its normalized version.
When considering the complex envelope of PSK signals

where  , the wavelet transform is given by
, the wavelet transform is given by

It is clear from (17) that for a certain scale value, the  of PSK signals is almost a constant function. Given the normalized signal
of PSK signals is almost a constant function. Given the normalized signal

the  is shown to be constant. Also, normalization will not affect wavelet transform of PSK signals since it is a constant envelope signal. Figure 3 shows the constant CWT magnitudes of 16-PSK signal and its normalized version.
is shown to be constant. Also, normalization will not affect wavelet transform of PSK signals since it is a constant envelope signal. Figure 3 shows the constant CWT magnitudes of 16-PSK signal and its normalized version.
For FSK, the complex envelope is defined by:

where  and
and  is the initial phase. From (19), the wavelet transform of FSK signal is given by
is the initial phase. From (19), the wavelet transform of FSK signal is given by

and the  of FSK signal is a multi-step function with
of FSK signal is a multi-step function with  being a variable. Also, the FSK normalized signal is given by
being a variable. Also, the FSK normalized signal is given by

One can show that  of the normalized FSK is a multi-step function. This is clear from Figure 4, where we show the CWT magnitudes for 16-FSK and its normalized version.
of the normalized FSK is a multi-step function. This is clear from Figure 4, where we show the CWT magnitudes for 16-FSK and its normalized version.
Finally, we consider MSK as a special case of continuous phase-frequency shift keying (CPFSK) with modulation index 0.5. The CWT magnitude of MSK signal is expected to be a two-step function similar to 2-FSK signal (Figure 5).
3. Features Extraction
Previous observations show the following.
-
(i)
The
 of PSK signals is constant while
of PSK signals is constant while  of ASK, FSK, MSK, and QAM signals is multi-step function.
of ASK, FSK, MSK, and QAM signals is multi-step function. -
(ii)
The
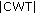 of the normalized ASK, PSK, and QAM signals is constant while the
of the normalized ASK, PSK, and QAM signals is constant while the 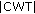 of normalized FSK and MSK signals is multi-step function.
of normalized FSK and MSK signals is multi-step function. -
(iii)
The statistical properties including the mean, the variance, and higher order moments (HOM) of wavelet transforms are different from modulation scheme to another. These statistical properties also differ depending on the order of modulation, since the frequency, amplitude, and other signal properties may change depending on the modulation order.
-
(iv)
There are distinct peaks in wavelet transforms of different modulated signals and their normalized ones when the Haar wavelet covers a symbol change. Note that the median filtering helps in removing these peaks which will affect
 statistical properties.
statistical properties.
According to the above observations, we propose a feature extraction procedure as follows. The CWT can extract features from a digitally modulated signal. These features can be collected by examining the statistical properties of wavelet transforms of both the signal and its normalized one. Since median filtering affects the statistical properties, these properties will be calculated with and without applying filtering. Based on our simulations, we noted that moments of order higher than five will not improve the overall performance of our algorithm. Therefore, in what follows, we consider moments of order up to five to calculate the HOM of wavelet transforms.
Figure 6 shows the processing chain of features extraction. As shown, the digitalized received signal is first normalized then the CWT of the received signal and the normalized one are obtained where the first subset of features will be the HOM (up to 5). A median filter is then applied to cut off the peaks in the corresponding wavelet transforms. Finally the HOM of these two filtered transforms will form the other features subset. This large number of features may contain redundant information about the signal. However, these features will surely have the necessary information to distinguish between different modulations. In order to select a smaller number of features a subset selection algorithm is proposed.
4. Classifier
The considered ADMR approach is divided into two subsystems: the features extraction subsystem and the classifier subsystem as shown in Figure 7. The ADMR problem (after features extraction) can be considered as a data classification problem. When the proper features are extracted, one can choose any good algorithm for classification, that is, the classification process is independent from the features extraction process. Some works use the thresholds and decisions trees to classify modulation schemes [11, 13], and others employ ANNs to achieve that [4–7].
ANNs were widely employed in the last decades, and they are among the best solutions for pattern recognition and data classification problems. ANNs were proven to increase the recognition performance of modulated signals. For instance the authors in [7] introduced two algorithms for analog and digital modulations recognition based on the spectral features of the modulated signal. It was shown that the first decision-theoretic algorithm has a poorer performance than the second ANN-based one. In this study, the proposed classifier is a multi-layer feed-forward neural network.
4.1. Artificial Neural Network
ANN is an emulation of biological neural system. ANN is configured through a learning process for a specific application, such as pattern recognition. ANNs with their remarkable ability to derive meaning from complicated or imprecise data can be used to extract patterns that are too complex to be noticed by other computer techniques.
ANN usually consists of several layers. Each layer is composed of several neurons or nodes. The connections among each node and the other nodes are characterized by weights. The output of each node is the output of a transfer function which its input is the summed weighted activity of all node connections. Each ANN has at least one hidden layer besides the input and the output layers. There are two known architectures of ANNs: the feed-forward neural networks and the feedback ones. There are several popular feed-forward neural network architectures such as multi-layer perceptrons (MLPs), radial basis function (RBF) networks, and self-organizing maps (SOMs). We had chosen MLP feed-forward networks in our work because of their simplicity and effective implementations; also they are extensively used in pattern recognition and data classification problems.
4.2. Artificial Neural Network Size
The network size includes the number of hidden layers and the number of nodes in each hidden layer. The network size is an important parameter that affects the generalization capability of ANN. Of course, the network size depends on the complexity of the underlying scenario where it is directly related to network training speed and recognition precision. In this paper the network size has been chosen through intensive simulations.
An improvement can be carried out to our work by using an algorithm that can automatically optimize the neural network size by balancing the minimum size and the good performance, since it is harder to manually search the optimal size. There are several techniques that help to approach the optimal size; some of them starts with huge network size and try to prune it toward the optimal size [26], others start with small network size and try to increase it toward the optimal size [27], and some works combine both the pruning and the growing algorithms [28].
Cascade-correlation algorithm (CCA) attempts to automatically choose the optimal network size [27]. Instead of just adjusting the weights in a network of fixed topology, CCA begins with a minimal network, and then automatically adds new hidden nodes one by one, creating a multi-layer structure. For each new hidden node, CCA attempts to maximize the magnitude of the correlation between the new node's output and the residual error signal which CCA is trying to eliminate.
4.3. Features Subset Selection
The large number of extracted features causes that some among them share the same information content. This will lead to a dimensionality problem. The obvious solution is the features selection, that is, reducing the dimension by selecting some features and discarding the rest. A features space with a smaller dimension will allow more accurate classification (regardless the classifier) due to data organization and projecting data to another space in which the discrimination is more obvious. The output of the features selection process is the input of the feed-forward neural network. Then, features selection also affects the neural network convergence and allows speeding its learning process and reducing its size. Among several possible features selection algorithms, we will investigate principal component analysis (PCA) and linear discriminate analysis (LDA).
PCA constructs a low-dimensional representation of the data (extracted features) that describes as much of the variance in that data as possible. PCA is mathematically defined as an orthogonal linear transformation that transforms the data to a new space such that the greatest variance by any projection of the data comes to lie on the first dimension (called the first principal component), the second greatest variance on the second dimension, and so on [29]. This moves as much of the variance as possible into the first few dimensions. The values in the remaining dimensions, therefore, tend to be highly correlated and may be dropped with minimal loss of information. PCA is the simplest of the true eigenvector-based multivariate analyses.
Let us suppose that  is the input data (extracted features). PCA attempts to find the linear transformation
is the input data (extracted features). PCA attempts to find the linear transformation  which maximizes
which maximizes  , where
, where  is the covariance matrix of the zero-mean data. It can be shown that
is the covariance matrix of the zero-mean data. It can be shown that  is formed of the first d principal eigenvectors (i.e., principal components) corresponding to the greatest d eigenvalues of the covariance matrix. The selected features are given by
is formed of the first d principal eigenvectors (i.e., principal components) corresponding to the greatest d eigenvalues of the covariance matrix. The selected features are given by

LDA is a supervised technique that attempts to maximize the linear separability between data points (features) belonging to different classes (targeted modulation schemes) [30]. It does so by taking into consideration the scatter between-classes besides the scatter within-classes, that is, finds a linear transform so that the between-classes variance is maximized, and the within-classes variance is minimized. The within-classes scatter  and the between-classes scatter
and the between-classes scatter  are defined as
are defined as

where  is the set of possible classes (modulation schemes),
is the set of possible classes (modulation schemes),  is the prior of class
is the prior of class  ,
,  is a data point of class
is a data point of class  ,
,  is the mean of class
is the mean of class  and
and  represents the mean of all classes. LDA attempts to find the linear transformation
represents the mean of all classes. LDA attempts to find the linear transformation  which maximizes the so-called Fisher criterion:
which maximizes the so-called Fisher criterion:

LDA seeks to find directions along which the classes are best separated. On the other side, PCA is based on the data covariance which characterizes the scatter of the entire data. Although one might think that LDA should always outperform PCA (since it deals directly with class separation), empirical evidence suggests otherwise [31]. For instance, LDA will fail when the discriminatory information is not in the mean but rather in the variance of the data.
Here, a modulation recognition performance comparison shows that LDA slightly outperforms PCA in the poor recognition region, and the performance of the two algorithms rapidly converges as the SNR goes high. Anyway, we will use PCA due to its simplicity and direct implementation.
4.4. Training Algorithm
The classification process basically consists of two phases: training phase and testing phase. A training set is used in supervised training to present the proper network behavior, where each input to the network is introduced with its corresponding correct target. As the inputs are applied to the network, the network outputs are compared to the targets. The learning rule is then used to adjust weights and biases of the network in order to move the network outputs closer to the targets until the network convergence. The training algorithm is mostly defined by the learning rule, that is, the weights update in each training epoch. There are a number of efficient training algorithms for ANNs. Among the most famous is the backpropagation algorithm (BP). An alternative is BP with momentum and learning rate to speed up the training. The weight values are updated by a simple gradient descent algorithm

The learning rate,  , scales the derivative, and it has a great influence on training speed. The higher learning rate is, the faster convergence is but with possible oscillation. On the other hand, a small learning value means too many steps are needed to achieve convergence. A variant of BP with adaptive learning rate can be used. The learning rate is adaptively modified according to the observed behavior of the error function. A BP algorithm employs the momentum parameter,
, scales the derivative, and it has a great influence on training speed. The higher learning rate is, the faster convergence is but with possible oscillation. On the other hand, a small learning value means too many steps are needed to achieve convergence. A variant of BP with adaptive learning rate can be used. The learning rate is adaptively modified according to the observed behavior of the error function. A BP algorithm employs the momentum parameter,  , to scale the influence of the previous step on the current. The momentum parameter is believed to render the training process more stable and to accelerate convergence in shallow regions of the error function. However, as practical experience has shown, this is not always true. It turns out in fact, that the optimal value of the momentum parameter is equally problem-dependent as the learning rate.
, to scale the influence of the previous step on the current. The momentum parameter is believed to render the training process more stable and to accelerate convergence in shallow regions of the error function. However, as practical experience has shown, this is not always true. It turns out in fact, that the optimal value of the momentum parameter is equally problem-dependent as the learning rate.
In this paper, we consider the resilient backpropagation algorithm (RPROP) [32]. Basically, RPROP performs a direct adaptation of the weight update based on local gradient information. Only the sign of the partial derivative is used to perform both learning and adaptation. In doing so, the size of the partial derivative does not influence the weight update.
The adaptive update-value  for RPROP algorithm was introduced as the only factor that determines the size of the weight update.
for RPROP algorithm was introduced as the only factor that determines the size of the weight update.  evolves during the learning process based on the local behavior of the error function
evolves during the learning process based on the local behavior of the error function  , according to the following learning rule:
, according to the following learning rule:

 . The direct adaptation works as follows. Whenever the partial derivative of the corresponding weight changes its sign, which implies that the last update was too large, and the algorithm jumped over a local minimum, the update-value is decreased by the factor
. The direct adaptation works as follows. Whenever the partial derivative of the corresponding weight changes its sign, which implies that the last update was too large, and the algorithm jumped over a local minimum, the update-value is decreased by the factor  . If the derivative retains its sign, the update-value is slightly increased (
. If the derivative retains its sign, the update-value is slightly increased ( ) in order to accelerate convergence in shallow regions.
) in order to accelerate convergence in shallow regions.
Once the update-value for each weight is updated, the actual weight update follows a very simple rule as shown in the following equations:

If the partial derivative is positive (i.e., increasing error), the weight is decreased by its update-value. If the derivative is negative, the update-value is added.
To summarize, the basic principle of RPROP is the direct adaptation of the weight update-value. In contrast to learning rate-based algorithms, RPROP modifies the size of the weight update directly based on resilient update-values. As a result, the adaptation effort is not blurred by unforeseeable gradient behavior. Due to the clarity and simplicity of the learning rule, there is only a slight expense in computation compared with ordinary backpropagation.
Besides fast convergence, one of the main advantages of RPROP lies in the fact that no choice of parameters and initial values is needed at all to obtain optimal or at least nearly optimal convergence times [32]. Also, RPROP is known by its high performance on pattern recognition problems.
After pre-processing and features subset selection, the training process is triggered. The initiated feed-forward neural network is trained using RPROP algorithm. Finally, the test phase is launched and the performance is evaluated through confusion matrix and false recognition probability. Some authors try to explain their results through receiver operating characteristic (ROC) which is more suitable for decision-theoretic approaches where thresholds normally classify modulation schemes.
5. Results and Discussion
The proposed algorithm was verified and validated for various orders of digital modulation types including ASK, PSK, MSK, FSK, and QAM. Table 1 shows the parameters used for simulations. Testing signals of 100 symbols are used as input messages for different values of SNR and channel effects (AWGN channel is used unless otherwise mentioned).
The wavelet transforms were calculated, and the median filter was applied to extract the features set. Then, pre-processing and features subset selection of 100 realizations of each modulation type/order is performed as a preparation of ANN training. The performance of the classifier was examined for 300 realizations of each modulation type/order, and the results are presented using the confusion matrix and false recognition probability (FRP).
The problem of modulation recognition will be investigated with three scenarios: (i) inter-class recognition (identify the type of modulation only), (ii) intra-class recognition (identify the order of known type of modulation), and (iii) full-class recognition (identify the type and order of the modulation at the same time), as shown in Figure 8.
5.1. Performance over AWGN Channel
The proposed classifier has shown an excellent performance over AWGN channel even at low SNR. Table 2 shows that full-class recognition of modulation schemes (16-QAM, 32-QAM, 64-QAM, 2-PSK, 8-PSK, 4-ASK, 8-ASK, 4-FSK, 8-FSK, and MSK) is achieved with high percentage when the SNR is not lower than 4 dB. Repeating the previous simulations for lower SNR values shows that the full-class recognition gives the lowest percentage for PSK signals.
Simulation results in Table 3 show that when the SNR is not lower than 3 dB, the percentage of correct inter-class recognition of ASK, FSK, MSK, PSK, and QAM modulations (case I) is higher than 99%. For lower SNR values, our results show that the inter-class recognition gives the lowest percentage for PSK and FSK, but the inter-class modulation recognition will remain robust for lower SNR values for QAM and ASK signals. We note that, reducing the modulation pool used in simulations to QAM, ASK, and FSK (case II) shows a high percentage of correct inter-class modulation recognition for lower SNR value ( dB), as shown in Table 4.
dB), as shown in Table 4.
Our results show that the intra-class recognition of modulation order using the proposed classifier gives different results depending on the modulation type. For instance, our simulations show that this recognition will be better for ASK and QAM signals than other modulation types, where a high percentage of correct modulation recognition is evident. This property can help in building an adaptive modulation system that assures high quality of service.
Tables 5 and 6 show the percentage of correct intra-class modulation recognition at very low SNR for QAM and ASK modulations, respectively. Also Tables 7 and 8 show the percentage of correct intra-class modulation recognition for FSK at SNR = 2 dB and PSK at SNR = 4 dB, respectively. The above results demonstrate that our algorithm can achieve high percentage with low SNR for non-constant envelop signals, while it can still achieve the same performance but with higher SNR for constant envelope signals.
Figure 9 shows the performance of the FRP for several recognition cases, where each graph represents FRP when the SNR is not lower that certain value. A minimum SNR for which the FRP is less than 1%,  has been considered in these results. Accordingly, the
has been considered in these results. Accordingly, the  for inter-class recognition (Case I) is 3 dB, for inter-class recognition (Case II) is
for inter-class recognition (Case I) is 3 dB, for inter-class recognition (Case II) is  dB, for intra-class PSK recognition is 4 dB, and for intra-class FSK recognition is 2 dB. Generally one can notice that the performance depends on the studied scenario, and it will drop down rapidly for SNRs less than
dB, for intra-class PSK recognition is 4 dB, and for intra-class FSK recognition is 2 dB. Generally one can notice that the performance depends on the studied scenario, and it will drop down rapidly for SNRs less than  . This also justifies the SNR values used in producing the results in Tables 2–8 and the corresponding high percentage of recognition observed since these SNRs represent the
. This also justifies the SNR values used in producing the results in Tables 2–8 and the corresponding high percentage of recognition observed since these SNRs represent the  for each case.
for each case.
5.2. Algorithm Parameters Optimization
We note that the scaling factor of the CWT has a great effect on the final performance of the classifier. Through extensive simulations, the optimum scaling factor was found to be 10 samples.
Extensive simulations show that the optimal ANN structure to be used for this algorithm is a two hidden layers network (excluding the input and the output layer), where the first layer consists of 10 nodes and the second of 15 nodes.
Let us examine the effect of the number of received symbols,  , on the algorithm performance. The results of this investigation are shown in Figure 10, where the FRP for several recognition cases is shown at a prescribed
, on the algorithm performance. The results of this investigation are shown in Figure 10, where the FRP for several recognition cases is shown at a prescribed  . Similar to the definition of
. Similar to the definition of  , we define
, we define  as the minimum
as the minimum  value for which FRP is less than 1%. We found that
value for which FRP is less than 1%. We found that  for inter-class recognition (Case I) is 100 symbols, for full-class recognition is 100 symbols, for intra-class FSK recognition is 75 symbols, and for intra-class QAM recognition is 50 symbols.
for inter-class recognition (Case I) is 100 symbols, for full-class recognition is 100 symbols, for intra-class FSK recognition is 75 symbols, and for intra-class QAM recognition is 50 symbols.
Generally one can notice that the performance depends on the studied scenario, and it will drop down rapidly for number of symbols less than  .
.
Figure 11 shows a performance comparison between the two features selection algorithms PCA and LDA. The FRP for inter-class modulation recognition (case II) was examined versus SNR when using each selection algorithm. It is clear that LDA slightly outperforms PCA in the poor recognition region (when  ). But the two algorithms have the same performance when
). But the two algorithms have the same performance when  , that is, when the recognition algorithm is well performing. However, in our work we have preferred PCA due to its simplicity and direct implementation.
, that is, when the recognition algorithm is well performing. However, in our work we have preferred PCA due to its simplicity and direct implementation.
So far our results are based on Haar wavelet. Now we examine the proposed algorithm using different wavelet families seeking the optimal wavelet filter to be used. In particular, we provide in Table 9 the total recognition percentage using several wavelet filters in the case of full-class recognition for SNR = 1 dB.
Using Haar wavelet, our previous results show that the  for full-class recognition is 4 dB. That is the reason why the algorithm performance has been investigated at SNR = 1 dB. The poor performance of the algorithm when using Haar wavelet is obvious in comparison to other wavelet families. However, the Haar wavelet, compared to other wavelets, enjoys the simplicity and the easiness of its mathematical modeling. Table 9 shows that the best performance will be found when using Meyer, Morlet, and Biorthgonal 3.5 wavelets. Note that the choice of the best wavelet filter depends on the algorithm implementation and computational complexity of the CWT.
for full-class recognition is 4 dB. That is the reason why the algorithm performance has been investigated at SNR = 1 dB. The poor performance of the algorithm when using Haar wavelet is obvious in comparison to other wavelet families. However, the Haar wavelet, compared to other wavelets, enjoys the simplicity and the easiness of its mathematical modeling. Table 9 shows that the best performance will be found when using Meyer, Morlet, and Biorthgonal 3.5 wavelets. Note that the choice of the best wavelet filter depends on the algorithm implementation and computational complexity of the CWT.
5.3. Performance over Fading Channels
Most of the existing works in the literature had examined their methods over AWGN channel. Here, we also developed our mathematical model and tested our algorithm over this channel. It is clear that it be will more realistic to examine the proposed algorithm performance over fading channels.
The performance of our algorithm has been evaluated in the case of full-class recognition when the SNR is not lower than 4 dB over different fading channels. The examined channel models were derived for the standards and specifications: GSM/EDGE channel models (3GPP TS 45.005 V7.9.0 (2007-2)) [33], COST 207 channel models [34], and ITU-R 3G channel models (ITU-R M.1225 (1997-2)) [35]. Simulations results in Table 10 show a high modulation recognition percentage over fading channels. This confirms that our algorithm has a robust performance regardless of the channel model used.
Finally in Figure 12, we present the FRP as a function of the mobile speed  in a GSM system considering the channel model of rural area (RAx, 6 taps) as introduced in the 3GPP GSM/EDGE channel model. It is clear from these results that the algorithm performance is better over fading channels than static ones. These results confirm the special capabilities of wavelet analysis relative to conventional analysis.
in a GSM system considering the channel model of rural area (RAx, 6 taps) as introduced in the 3GPP GSM/EDGE channel model. It is clear from these results that the algorithm performance is better over fading channels than static ones. These results confirm the special capabilities of wavelet analysis relative to conventional analysis.
5.4. Performance Comparison
The comparison among different modulation recognition algorithms is not straightforward. This is mainly because of the fact that there are no available standard digital modulation databases. Hence, different works have applied their algorithms to cases of their own choosing [10].
Also, the different studies considered different modulation pools and different simulation configurations which will result in different and incomparable performances. Some algorithms need a priori information of the signal, for example, carrier frequency [4, 6], frequency offset [9], and channel information [3].
The authors in [4] employed HOC and HOM of the baseband recovered complex envelope. A feed-forward neural network trained with RPROP algorithm was used as a classifier. The modulation schemes M-PSK, M-ASK, and M-QAM were examined. The performance of their classifier is higher than 93% for SNR  4 dB and 98% when SNR
4 dB and 98% when SNR  8 dB. In [11], the developed algorithm was verified using wavelet transform and histogram computations to identify M-PSK, M-QAM, M-FSK and GMSK. When SNR is above 5 dB, the probability of detection of this algorithm is more than 97.8%. In [20], the perfect classification between M-PSK signals can be obtained when SNR
8 dB. In [11], the developed algorithm was verified using wavelet transform and histogram computations to identify M-PSK, M-QAM, M-FSK and GMSK. When SNR is above 5 dB, the probability of detection of this algorithm is more than 97.8%. In [20], the perfect classification between M-PSK signals can be obtained when SNR  8 dB (considering 256 symbols) and SNR
8 dB (considering 256 symbols) and SNR  10 dB (considering 100 symbols).
10 dB (considering 100 symbols).
A comparison between our results and the above-mentioned ones will show the high performance of our algorithm. The recognition probability of M-ASK, M-PSK, M-QAM, M-FSK, and MSK is higher than 99% when SNR is not lower than 4 dB. M-PSK signals classification percentage is higher than 99% when SNR is not lower than 4 dB (considering 100 symbols). Initially our work was based on that introduced in [13]. Simulations on the same modulation pool examined in [13] (16-QAM, 4-PSK, and 4-FSK) show that our recognition percentage is higher than 99% when SNR is not lower than  dB. This outperforms the algorithm proposed in [13], where the percentage of correct recognition was about 97% when SNR is greater than 5 dB. Not very much modulation recognition studies investigated the robustness of their methods over fading channels. The authors in [3, 15] considered the Rayleigh fading channel model.
dB. This outperforms the algorithm proposed in [13], where the percentage of correct recognition was about 97% when SNR is greater than 5 dB. Not very much modulation recognition studies investigated the robustness of their methods over fading channels. The authors in [3, 15] considered the Rayleigh fading channel model.
It is essential to focus on the fact that in our algorithm the different modulated signals are digitalized in RF or IF stages (the carrier frequency is unknown) with respect to SDR principles. The recognition is done without any priori signal information, and our algorithm shows robustness over fading channels.
6. Conclusion
We presented a wavelet-based algorithm for automatic modulation recognition. The proposed algorithm is capable of recognizing different modulation schemes with high accuracy at low SNRs. Our classifier has high full-class modulation recognition performance when the SNR is not lower than 4 dB. We found that the percentage of correct inter-class recognition for MSK, FSK, ASK, PSK, and QAM is high when the SNR is not lower than 3 dB. Also, the percentage of the correct intra-class recognition of modulation order was found to be high for low SNRs, and the minimum value of SNR for which the high percentage of intra-class recognition is still reachable depends on the modulation type, and could reach a very low value ( dB for intra-class QAM recognition). In addition, we have shown that our algorithm offers excellent performance over both AWGN and several fading channel models.
dB for intra-class QAM recognition). In addition, we have shown that our algorithm offers excellent performance over both AWGN and several fading channel models.
References
Dobre OA, Abdi A, Bar-Ness Y, Su W: Survey of automatic modulation classification techniques: classical approaches and new trends. IET Communications 2007, 1(2):137-156. 10.1049/iet-com:20050176
Wei W, Mendel JM: Maximum-likelihood classification for digital amplitude-phase modulations. IEEE Transactions on Communications 2000, 48(2):189-193. 10.1109/26.823550
Dobre OA, Hameed F: Likelihood-based algorithms for linear digital modulation classification in fading CHANNELS. Proceedings of the Canadian Conference on Electrical and Computer Engineering (CCECE '06), 2006, Ottawa, Canada 1347-1350.
Ebrahimzadeh A, Ranjbar A: Intelligent digital signal-type identification. Engineering Applications of Artificial Intelligence 2008, 21(4):569-577. 10.1016/j.engappai.2007.06.003
Zhao Y, Ren G, Zhong Z: Modulation recognition of SDR receivers based on WNN. Proceedings of the 63rd IEEE Vehicular Technology Conference (VTC '06), May 2006 2140-2143.
Wong MLD, Nandi AK: Automatic digital modulation recognition using artificial neural network and genetic algorithm. Signal Processing 2004, 84(2):351-365. 10.1016/j.sigpro.2003.10.019
Nandi AK, Azzouz EE: Algorithms for automatic modulation recognition of communication signals. IEEE Transactions on Communications 1998, 46(4):431-436. 10.1109/26.664294
Swami A, Sadler BM: Hierarchical digital modulation classification using cumulants. IEEE Transactions on Communications 2000, 48(3):416-429. 10.1109/26.837045
Dobre OA, Bar-Ness Y, Su W: Robust QAM modulation classification algorithm using cyclic cumulants. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '04), 2004 745-748.
Mobasseri BG: Digital modulation classification using constellation shape. Signal Processing 2000, 80(2):251-277. 10.1016/S0165-1684(99)00127-9
Prakasam P, Madheswaran M: Modulation identification algorithm for adaptive demodulator in software defined radios using wavelet transform. International Journal of Signal Processing 2009, 5(1):74-81.
Maliatsos K, Vassaki S, Constantinou P: Interclass and intraclass modulation recognition using the wavelet transform. Proceedings of the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007
Hong L, Ho KC: Identification of digital modulation types using the wavelet transform. Proceedings of the IEEE Military Communications Conference (MILCOM '99), November 1999 427-431.
Lichun L: Comments on "Signal classification using statistical moments". IEEE Transactions on Communications 2002, 50(2):195. 10.1109/26.983315
El-Mahdy AE, Namazi NM: Classification of multiple M-ary frequency-shift keying signals over a Rayleigh fading channel. IEEE Transactions on Communications 2002, 50(6):967-974. 10.1109/TCOMM.2002.1010616
Liedtke FF: Adaptive procedure for automatic modulation recognition. Journal of Telecommunications and Information Technology 2004, (4):91-97.
Wu Z, Ren G, Wang X, Zhao Y: Automatic digital modulation recognition using wavelet transform and neural networks. Proceedings of the International Symposium on Neural Networks (ISNN '04), 2004, Lecture Notes in Computer Science 3173: 936-940.
Wu Z, Wang X, Liu C, Ren G: Automatic digital modulation recognition based on ART2A-DWNN. Proceedings of the 2nd International Symposium on Neural Networks (ISNN '05), June 2005, Lecture Notes in Computer Science 3497: 381-386.
Dayoub I, Okassa-M'Foubat A, Mvone R, Rouvaen JM: A blind modulation type detector for DPRS standard. Wireless Personal Communications 2007, 41(2):225-241. 10.1007/s11277-006-9140-8
Pedzisz M, Mansour A: Automatic modulation recognition of MPSK signals using constellation rotation and its 4th order cumulant. Digital Signal Processing 2005, 15(3):295-304. 10.1016/j.dsp.2004.12.007
Li J, He C, Chen J, Wang D: Automatic digital modulation recognition based on euclidean distance in hyperspace. IEICE Transactions on Communications 2006, 89(8):2245-2248.
Tadaion AA, Derakhtian M, Gazor S, Nayebi MM, Aref MR: Signal activity detection of phase-shift keying signals. IEEE Transactions on Communications 2006, 54(8):1439-1445.
Avci E, Hanbay D, Varol A: An expert discrete wavelet adaptive network based fuzzy inference system for digital modulation recognition. Expert Systems with Applications 2007, 33(3):582-589. 10.1016/j.eswa.2006.06.001
Su W, Xu JL, Zhou M: Real-time modulation classification based on maximum likelihood. IEEE Communications Letters 2008, 12(11):801-803.
Addison PS: Illustrated Wavelet Handbook. Institute of Physics, Dublin, Ireland; 2002.
Castellano G, Fanelli AM, Pelillo M: An iterative pruning algorithm for feedforward neural networks. IEEE Transactions on Neural Networks 1997, 8(3):519-531. 10.1109/72.572092
Fahlman SE, Lebiere C: The cascade-correlation learning architecture. Carnegie Mellon University; 1990. CMU-CS-90-100
Lin C-T, Lee C-C: Neural Fuzzy Systems: A Neuro-Fuzzy Synergism to Intelligent Systems. Prentice-Hall, New York, NY, USA; 1996.
Kwak N: Principal component analysis based on L1-norm maximization. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008, 30(9):1672-1680.
Fukunaga K: Introduction to Statistical Pattern Recognition. 2nd edition. Academic Press, New York, NY, USA; 1990.
Martinez AM, Kak AC: PCA versus LDA. IEEE Transactions on Pattern Analysis and Machine Intelligence 2001, 23(2):228-233. 10.1109/34.908974
Riedmiller M, Braun H: Direct adaptive method for faster backpropagation learning: the RPROP algorithm. Proceedings of the IEEE International Conference on Neural Networks, April 1993, San Francisco, Calif, USA 586-591.
Radio transmission and reception, 3GPP TS 45.005 3GPP Specification Series, 2007
Digital Land Mobile Radio Communications—COST 207 Commission of the European Communities, 1989
Guidelines for Evaluation of Radio Transmission Technologies for International Mobile Telecommunications—2000 ITU Radio Communication Sector (ITU-R), 1997
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hassan, K., Dayoub, I., Hamouda, W. et al. Automatic Modulation Recognition Using Wavelet Transform and Neural Networks in Wireless Systems. EURASIP J. Adv. Signal Process. 2010, 532898 (2010). https://doi.org/10.1155/2010/532898
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/532898





 of PSK signals is constant while
of PSK signals is constant while  of ASK, FSK, MSK, and QAM signals is multi-step function.
of ASK, FSK, MSK, and QAM signals is multi-step function.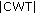 of the normalized ASK, PSK, and QAM signals is constant while the
of the normalized ASK, PSK, and QAM signals is constant while the 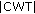 of normalized FSK and MSK signals is multi-step function.
of normalized FSK and MSK signals is multi-step function. statistical properties.
statistical properties.





