- Research
- Open access
- Published:
Bayesian fault detection and isolation using Field Kalman Filter
EURASIP Journal on Advances in Signal Processing volume 2017, Article number: 79 (2017)
Abstract
Fault detection and isolation is crucial for the efficient operation and safety of any industrial process. There is a variety of methods from all areas of data analysis employed to solve this kind of task, such as Bayesian reasoning and Kalman filter. In this paper, the authors use a discrete Field Kalman Filter (FKF) to detect and recognize faulty conditions in a system. The proposed approach, devised for stochastic linear systems, allows for analysis of faults that can be expressed both as parameter and disturbance variations. This approach is formulated for the situations when the fault catalog is known, resulting in the algorithm allowing estimation of probability values. Additionally, a variant of algorithm with greater numerical robustness is presented, based on computation of logarithmic odds. Proposed algorithm operation is illustrated with numerical examples, and both its merits and limitations are critically discussed and compared with traditional EKF.
1 Introduction
The problem of fault detection and isolation is one of the most important research topics in process control. Efficient methods should quickly detect the occurrence of a fault and determine the fault origin with sufficient probability. However, people usually have to deal with measurement disturbances, process noise, and complicated dynamics when analyzing the actual industrial processes. As the field is very broad for the purpose of this paper, we will focus on faults that can be represented by a change of either parameters in the mathematical model or parameters of stochastical disturbances of the analyzed system. Diagnosis and isolation of such faults relies on two elements—detecting the change in the parameter value and isolating what type of fault causes such change.
A typical approach to such estimation for linear distributed systems is the use of variations of Kalman filters, often used as residue generators, with some kind of classification algorithm. The problem of estimating the state of a linear dynamic system driven by additive Gaussian noise with unknown time varying statistics is considered in [1] through Kalman filtering with Bayesian methods for estimation of noise variance, while maximum likelihood is used in [2], and correlation methods are used in [3] and [4].
In [5], methodology for the detection and accommodation of actuator faults for a class of multi-input–multi-output (MIMO) stochastic systems is presented. Actuator fault diagnosis is based on the estimation of the state vector, where Kalman filter is used to estimate the state. A Kalman filter approach is proposed for state estimation for stochastic discrete-time linear systems in [6–9] while in [10–12], a Kalman filter is applied for estimation of state vector for non-linear systems. Model-based isolation and estimation of additive faults in discrete-time linear Gaussian systems is presented in [13], where fault estimation is carried out and a Kalman filter is used with Bayesian statistics. A novel sensor fault detection and isolation algorithm based on an extended Kalman filter is presented for noise and efficiency in real-time implementation in [14]. In the paper [15], a diagnostic system based on a uniquely structured Kalman filter is developed for its application to in-flight fault detection of aircraft engine sensors. A bibliographic review on a distributed Kalman filter is provided in [16] with a comparison to the different approaches. Very important group of methods for fault detection and isolation is based on particle filtering. This method, a certain extension of Kalman filtering, allows very good results in a wide spectrum of cases. The disadvantage can be however increased computational complexity. Important works on the subject are among the others [17–22].
It should be also noted that similar approach to system analysis is present in the issues of model selection and working point detection problems. First of this problems is used to verify which model of the possible group fits the best presented data. It is usually connected with some kind of hypothesis testing. The second group has a special place in the process control applications. It is very often encountered in industrial situations that the system is very hard to be modeled fully representing its nonlinear character. In such cases, a set of linearized models in different working points is created. Appropriate algorithm for choice of which linear model should now be used depending on data is very similar to fault detection and isolation one.
In this paper, the authors expand on their earlier results in [23], where the Field Kalman Filter was proposed. The Field Kalman Filter is an advanced signal processing algorithm which in its full form allows full estimation of state and parameters of linear systems with Gaussian disturbances. The main disadvantage of this filter is that in general case, it is infinite dimensional, and for practical applications, moving horizon approximation has to be used.
In this paper, we apply and modify this filter for the problem of fault detection and isolation. In particular, an advantage is taken over the fact that typical faults usually form a limited set of cases. In such situation, problem dimension reduces substantially, and the algorithm requires solution of a parameter-dependent family of systems of equations. Proposed filter is optimal for systems with fixed parameters and highly efficient for those where changes in parameter values occur. We present the algorithm for computing fault probability and also its more numerically robust version for computing logarithmic odds of fault occurrence with respect to each other possibility.
The rest of this paper is organized as follows. First, we present the Field Kalman Filter in the discrete case. Second, we formulate its application for fault detection and isolation problem. We formulate the necessary modification of the filter for parameter-varying systems with formulation of necessary forgetting operator. We discuss algorithms’ numerical drawbacks and introduce more robust modification. Then, we illustrate both algorithms’ operation with advanced examples of fault detection, where faults are either in parameters or in the disturbances. The paper ends with discussion, comparing our results to those based on EKF and conclusions regarding future work.
Remark 1
(Notation) We denote the set of symmetrical and positively defined matrices of dimension n by S +(n). By x∼N(m,S), we understand a normally distributed random variable with a mean m and a covariance matrix S. Also, we define function N(x,m,S) as
2 Field Kalman Filter
Let us consider the following stochastic system
We have the assumptions as following:
-
1.
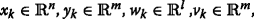 w
k
∼N(0,I), v
k
∼N(0,V(θ)),
w
k
∼N(0,I), v
k
∼N(0,V(θ)), 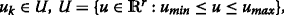 k=0,1,2,….
k=0,1,2,…. -
2.
Equations (2)–(3) depend on parameter vector
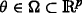 . The matrix functions A,B,G,C,V are of C
1 class w.r.t. both arguments and are of appropriate dimensions.
. The matrix functions A,B,G,C,V are of C
1 class w.r.t. both arguments and are of appropriate dimensions. -
3.
The prior distribution of parameter θ will be denoted by p 0. The set of all initial distributions of θ is defined as
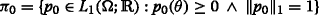 .
. -
4.
We assume that the initial joint distribution of the variables (x 0,θ) has the following form
$$ q_{0}(x_{0}, \theta)= p_{0}(\theta) N(x_{0},m_{0},S_{0}). $$(4)where
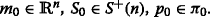
-
5.
The first measurement is performed at k=1, and
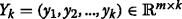 is a matrix of k first measurements.
is a matrix of k first measurements.
Remark 2
We define that observability of the parameters has the following property
In other words, we require that probabilities of different values of parameters conditional on the same set of measurements are different. In this paper, we assume that the parameters of all considered systems are observable.
In the following theorem, we provide a formula for calculating the distribution of the state and parameters of system (2)–(3), which we will call a Field Kalman Filter.
Theorem 1
Let u k be given by fixed sequence and let A i (θ)=A(θ,u i ), B i (θ)=B(θ,u i ), and D i (θ)=G(θ,u i )G(θ,u i )T. If assumptions 1–5 are fulfilled, then joint density of variables x k , θ, Y k is given by
where
Proof
The proof of a very similar theorem can be found in [23]. The difference is that here, we consider a discrete-time system instead of a continuous one. Nevertheless, there is a completely analogous distribution construction for these two types of time systems. □
To create a diagnostic algorithm, we will need the following corollary:
Corollary 1
Under the assumptions of Theorem 1, we have
and
Proof
It is a direct consequence of the Bayes’ theorem and Eq. (6). □
Now, we can formulate the fault detection problem.
3 Fault detection problem
Equations (14) and (15) are the solution to estimating the distributions of state and parameters. This solution (filter), in general, is infinite dimensional. It is caused by the fact that we need to solve Eqs. (7)–(13) for all the possible values of θ, in order to compute the necessary integral in Eq. (15). Because of this sizeable computation, it is greatly difficult to implement in practice.
Situation changes when the number of potential parameters in set Ω is finite. In this case, the integral in (15) becomes a summation operator. Consequently, Eqs. (7)–(13) only need to be calculated for a finite number of θ values.
This problem formulation, i.e., θ∈Ω={θ 0, θ 1, θ 2, …, θ r }, is not a common case for parameter estimation; however, it is greatly suited to a fault detection problem, when we already know what type of faulty conditions can occur in the system.
Next, we denote the parameter θ 0 as a normal operating condition. The parameters θ 1,θ 2,..,θ r represent system faults. The initial distribution of θ can be rewritten as
As a consequence, the distribution Eq. (15) becomes a discrete distribution
where,
Equation (18) can be rewritten in a more convenient, recursive form
Now, the distribution of (x k ,θ) conditioned on Y k takes the form
Equations (7)–(13), (19) and (20) describe the finite-dimensional recursive optimal filter for system (2)–(3). The set of functions m k (θ s ),S k (θ s ) with p k,0, p k,1, p k,2, …, p k,r determines the conditional distribution p(x k+1,θ∣y k+1) in the next time step.
3.1 Forgetting operator
In real practice, parameters are time varying and the old data must be gradually forgotten, as it becomes obsolete.
The estimator might not work properly on varying parameters. For example, when enough data supports fault θ j that up to numerical precision, we have p i,j =1 and p i,s =0 for s≠j, then from Eq. (19), we can see that adding new data, supporting different fault will not be registered (as its likelihood will be multiplied by 0).
It can be understood that if all the data, regardless of how old is it, has the same importance, then the new evidence for fault occurrence might be ignored.
To allow our estimator to handle time-varying parameters, we introduce a forgetting operator F. Let α∈(0,1) be a forgetting factor, and let  such that
such that
The operator F=[f ij ] r×r is a doubly stochastic matrix, i.e., \( {\sum _{i} f_{ij} = \sum _{j} f_{ij}=1}\). Multiplication of any probability distribution P k−1=(p 0,k−1, p 1,k−1, …, p r−1,k−1)T by F gives a new probability distribution P k =FP k−1. If α<1, then this new distribution has a greater entropy. Therefore, the amount of information about the parameters is reduced. The stationary distribution for F is uniform, i.e., \( {\lim }_{k \rightarrow \infty } F(\alpha)^{k} P_{0}= r^{-1} (1,1,..1)^{\mathsf {T}} \), for any initial distribution P 0. It should be noted that the choice of forgetting operator is not unique, as there are multiple possible operators that increase the entropy. In our case, we interpret the parameter α as the desired depth of the memory, where α=1 corresponds to infinite memory, a smaller alpha value corresponds to a faster forgetting rate. Proposed operator was chosen through practice and does not consider the option of instantaneous forgetting, as it was not needed.
3.2 Algorithm for fault estimation
Based on the above discussion, we can formulate the following algorithm for fault estimation.

Remark 3
(Calculation of conditional mean, covariance and most probable value of θ) Proposed algorithm can also be used to estimate actual values of state and parameters of the system through either mean and covariance or maximum a posteriori estimation. The following formulas can be used:
Remark 4
It needs to be emphasized that the case, when parameters vary over time, while practically significant, do not fulfill the original assumptions of the filter. Because of that, our filter, even with forgetting operator, is not optimal for the problem. However, as it can be seen in provided examples in Section 5, it is convergent in practice.
4 Improvement of numerical properties
We notice that mathematically, there is potential numerical instability in Eq. (29), which is caused by the fact that a large output error, i.e., \( |\!W(\theta _{s})^{-0.5} (y_{k} -C(\theta _{s})m_{k}^{-} (\theta _{s}))|\!>>1\), induces an extremely small value of p k,s . Consequently, Eq. (29) works out as a quotient of two extremely small numerical values which can cause a numerically intractable result. This numerical limitation was also observed and illustrated in a scalar system example demonstrated in Section 5 of our paper.
Therefore, to eliminate this numerical instability, we propose an alternative approach, using logarithmic odds (see for example [24]). Let us consider the logarithm of probability quotient i.e.
By substituting Eqs. (1) and (19) into (34), we get the following recursion
where
To use logarithmic odds to determine most probable fault, we need to verify for which fault θ s all the ratios e k,s,j are positive. Such fault has maximum a posteriori probability.
Whenever we have positive logarithmic odds for one parameter value \(\theta _{i_{MAP}} \) against others, i.e., \(e_{k,i_{MAP},j} \ge 0\) for all j=0,1,…,r, then it is the most probable value of the parameter, i.e., \(\phantom {\dot {i}\!}p_{k,j} \le p_{k,i_{MAP}} \).
Furthermore, to introduce the forgetting operation mentioned in Section 3.1, we can implement it as
where β∈[0, 1] is a new forgetting factor. The product of e k−1,i,j and β∈[0,1) corresponds to certain new distribution. This new distribution has greater entropy and is closer to a uniform distribution. Hence, if β∈(0,1), the old data need to be gradually forgotten. If β=0, then e k,i,j =0 and p k,i =p k,j for all i,j=1,…,r. If β=1, it means that all the old data are supposed to be taken into account.
Now, we can propose a logarithmic odds algorithm for fault detection and classification:
5 Examples of operation
In this section, we illustrate the algorithm operation using three examples of linear systems. In the first one, we use Algorithm 1 for a scalar discrete system, where all elements of the system depend on the parameters (i.e., state, control and output). In the second example, we use the same algorithm for a second-order, time continuous system, with discrete-time observation, parameter-dependent state, control and noise matrices, and noise variance. The final example uses the same system to illustrate the log-odds Algorithm 2.

5.1 Example 1. Scalar system with changes in parameters
Let us consider the following scalar system
In this system, we consider a normal operation state and four fault cases. The settings of these cases are shown in Table 1. The first fault corresponds to increase in system dynamics, combined with substantial increase of system gain. The second fault introduces system oscillation but a lesser gain increase. The third fault slightly increases systems’ dynamics, increases input gain, and decreases output gain. The fourth fault introduces a larger increase in the dynamics than the third, but with smaller increment in input gain and lower reduction in output gain.
The initial conditions of the filter were set as m 0(θ)=0 and S 0(θ)=0.01. The initial probability distribution of faults was p 0=[0.95, 0.0125, 0.0125, 0.0125, 0.0125]. The simulation of system started with normal operation conditions. Then, after every 200 steps, the operating mode was changed in such a scheme: normal, fault 1, fault 2, fault 3, fault 4, fault 3, fault 2, fault 1, and normal. The system was excited by a square input signal u with zero mean, a period of 158, and the amplitude as 1. We set the forgetting factor as α=0.99, which is experimentally efficient.
We present the measured signal in Fig. 1. We have applied the algorithm to this signal. Using Eq. (29), we computed the probabilities of particular faults and presented them in the Fig. 2. We can observe consistency between maximal probability and the planned test regime of faults occurring. It is evident in Fig. 3, where the results of fault detection and isolation are presented based on maximum a posteriori estimate.
Measured output signal for the system (45) with operating conditions changing every 200 samples
Probability of which operation state system (45) is in conditional on the measurements. Probabilities are computed using formula (29)
The results show that estimator reacts very quickly, usually within five samples detecting a change in the parameter value. The numerical instability, described in Section 4, occurs and is visible in the Fig. 3.
5.2 Example 2. Oscillator with unknown noise variances
Let us consider a second-order continuous time system (oscillator) given by
with discrete-time observation
where ξ=0.1 and b c =1. The initial condition is Gaussian, i.e., x(0)∼N(m 0,S 0). We can see that this is a system with varying natural frequency, varying process, and measurement noise variances.
Assuming that control u is a piecewise constant, i.e., u(t)=u k , t∈[t k−1, t k ), we can discretize system (46)–(47). The discrete-time system corresponding to Eqs. (46)–(47) has the form
where matrices A, B, and D can be calculated from the formulas
G(θ) is non-uniquely defined as a factor of D(θ)=G(θ)G(θ)T. However, it is not needed for filter computation. In addition, it should be noted that discretization operation (49) increases the nonlinearity of system dependence on parameters. The discretization step is T 0=0.05.
In this example, noise variances θ 2 and θ 3 are unknown and must be estimated, which is not a typical task. We consider four cases: normal operating conditions, change in the oscillator natural frequency (fault 1), increase in process noise variance by an order of magnitude (fault 2), and increase in measurement noise by an order of magnitude (fault 3). Values of parameters corresponding to normal operating conditions and faults are shown in Table 2.
The simulation was started with normal conditions. Next, after every 2500 steps (125 s), the operating mode was changed according to the scheme as normal, fault 1, fault 2, and fault 3. The input u was a zero mean, square signal. The forgetting factor α was 0.99. Measurements are presented in Fig. 4. Probabilities obtained with Eq. (33) are presented in Fig. 5. Again, in this case, faults with maximum probability correspond to the fault schedule.
Measured output signal for the oscillator (46) with operating conditions changing every 2500 samples
Probability of which operation state the oscillator (46) is in conditional on the measurements. Probabilities are computed using formula (29)
5.3 Example 3. Oscillator with unknown noise variances—logarithmic odds approach
In this example, we analyze the same second-order continuous time system as in the example 2. The settings of parameters were as ξ=0.1, b c =1, T 0=0.05, m 0=(0, 0)T, and S 0=10−2 I. Initial distribution was uniform. The fault case 3 is now different than in the previous example, as the natural frequency also changes.
The simulation started with the normal conditions. Next, after every 2500 steps, the operating mode was changed in the scheme as normal, fault 1, fault 2, fault 3, and normal (see Table 3). The input u was a zero mean, square signal with a period of 630. The forgetting factor β= was 0.995. The estimation results are shown in Fig. 6. We can see that there are no numerical errors; however, there is a case of wrongly identified fault, when fault 2 is identified instead of normal state for a short time (comparing with a schedule).
We can reconstruct the probabilities from log-odds using formula
and they are presented in Fig. 7. As one can see, the probability estimate is much less varying than in the case of using Algorithm 1.
6 Discussion
While proposed fault detection and isolation algorithm gives promising results, it is more than natural to compare it with the industry standard which is Extended Kalman Filter. We will now explain the differences between our approach and EKF.
The most important fact is that the Extended Kalman Filter (EKF) forms Gaussian approximation of true probability density of the state variables and parameters. The original state equations are extended by adding new equations which represent parameters as constant state variables. Prediction of their mean values is based on the extended system of state equations while the covariance matrix is calculated on the basis of linearized model. The correction step is the same as in the classical Kalman filter. Input noise and measurement noise covariances have to be known a priori and cannot be estimated by EKF. Due to the nonlinearity of the extended system, the EKF estimate can often diverge. In the considered fault isolation problem, the probability density of the parameter values is discrete and its Gaussian approximation formed by EKF is continuous, so it cannot represent their character properly.
All these issues suggest that EKF is not an optimal (or sufficiently sub-optimal) tool for the considered fault detection and isolation problem. Nevertheless, it is possible to apply EKF for this task, using it to estimate the parameter values and providing appropriate thresholding to isolate appropriate faults.
In contrast to EKF, the proposed Field Kalman Filter forms true density of the state and parameter if the forgetting factor is 1. Noise covariances need not to be known a priori and they can be estimated on the basis of data. Since FKF allows calculation of probabilities of particular faults it is possible to easily construct statistical tests for fault detection and isolation.
The only actual advantage of EKF over FKF is a substantially reduced computational complexity. FKF needs to solve a system of equations for every considered fault type, while EKF requires solution of only one system of equations (but with extended state). This reduction comes at a price; as for system with complicated parameter dependence (like the one in examples 2 and 3), EKF might not converge at all. Lack of convergence for parameter estimation (natural frequency of the oscillator) is presented in the Fig. 8.
7 Conclusions
We have presented two algorithms for fault estimation. Both of them are based on the proposed by the first two authors the Field Kalman Filter. Algorithm 1, i.e., direct application of FKF is attractive because it can be easily used for determination of fault probabilities, providing level of confidence in fault detection. There is however some numerical sensitivity connected to computations close to 0/0 operation.
At the cost of dropping, the direct probability computation one can use log-odds-based approach of the Algorithm 2. In this case, the problem of division by zero is reduced to addition and subtraction of numbers in the same order of magnitude. The main disadvantage is requirement of additional memory storage—with Algorithm 1, only the vector of r probabilities is needed, while Algorithm 2 requires a r×r matrix of logarithmic odds. Additionally, the result in form of odds can be complicated to interpret if the resulting probability distribution of faults is multi-modal. Original probabilities can be reconstructed but also with additional computational cost.
Additionally, as it was mentioned before, the forgetting operator is not unique. Proposed forgetting for Algorithms 1 and 2 are working properly for presented and other considered test systems. It should be however noted that they are not equivalent and their selection may require future work.
Future directions of work will include addressing the abovementioned issue, as well as implementation for more advanced systems. In particular, we want to extend the fault detection algorithm to the problems continuous in time. Additionally, the real-time performance of proposed algorithms will be tested in the laboratory environment systems.
References
D Alspach, A parallel filtering algorithm for linear systems with unknown time varying noise statistics. IEEE Trans. Autom. Control. 19(5), 552–556 (1974). doi:10.1109/TAC.1974.1100645.
R Kashyap, Maximum likelihood identification of stochastic linear systems. IEEE Trans Autom Control. 15(1), 25–34 (1970). doi:10.1109/TAC.1970.1099344.
BM Åkesson, JB Jørgensen, NK Poulsen, SB Jørgensen, in 17th European Symposium on Computer Aided Process Engineering, Computer Aided Chemical Engineering, 24, ed. by V Pleşu, PŞ Agachi. A tool for kalman filter tuning (Elsevier, 2007), pp. 859–864. doi:10.1016/S1570-7946(07)80166-0. http://www.sciencedirect.com/science/article/pii/S1570794607801660. Accessed 15 Nov 2017.
B Carew, P Belanger, Identification of optimum filter steady-state gain for systems with unknown noise covariances. IEEE Trans Autom Control. 18(6), 582–587 (1973). doi:10.1109/TAC.1973.1100420.
B Jiang, FN Chowdhury, Fault estimation and accommodation for linear mimo discrete-time systems. IEEE trans control syst technol. 13(3), 493–499 (2005).
J-y Keller, DDJ Sauter, Kalman Filter for discrete-time stochastic linear systems subject to intermittent unknown inputs. IEEE Trans Autom Control. 58(7), 1882–1887 (2013).
L Giovanini, R Dondo, A fault detection and isolation filter for discrete linear systems. ISA Trans. 42(4), 643–9 (2003).
S Huang, KK Tan, TH Lee, Fault diagnosis and fault-tolerant control in linear drives using the Kalman filter. IEEE Trans Ind Electron. 59(11), 4285–4292 (2012).
RH Chen, JL Speyer, A generalized least-squares fault detection filter. Int. J. Adapt. Control Sig. Process. 14(7), 747–757 (2000).
GG Rigatos, A derivative-free Kalman filtering approach to state estimation-based control of nonlinear systems. IEEE Trans. Ind. Electron. 59(10), 3987–3997 (2012).
W Li, SL Shah, D Xiao, Kalman filters in non-uniformly sampled multirate systems : For FDI and beyond. Automatica. 44:, 199–208 (2008). doi:10.1016/j.automatica.2007.05.009.
P Li, V Kadirkamanathan, Particle filtering based likelihood ratio approach to fault diagnosis in nonlinear stochastic systems. IEEE Trans Syst Man Cybern Part C: Appl Rev. 31(3), 337–343 (2001).
D Antônio, T Yoneyama, Automatica A Bayesian solution to the multiple composite hypothesis testing for fault diagnosis in dynamic systems. Automatica. 47(1), 158–163 (2011). doi:10.1016/j.automatica.2010.10.030.
GH Foo, X Zhang, S Member, DM Vilathgamuwa, S Member, A sensor fault detection and isolation method in interior permanent-magnet synchronous motor drives based on an extended Kalman filter. IEEE Trans. Ind. Electron. 60(8), 3485–3495 (2013).
T Kobayashi, DL Simon, Hybrid Kalman filter approach for aircraft engine in-flight diagnostics: sensor fault detection case. J. Eng. Gas Turbines Power. 129(3), 746–754 (2006). doi:10.1115/1.2718572.
MS Mahmoud, HM Khalid, Distributed Kalman filtering: a bibliographic review. IET Control. Theory Appl. 7(4), 483–501 (2013). doi:10.1049/iet-cta.2012.0732. http://ieeexplore.ieee.org/document/6544363/. Accessed 15 Nov 2017.
CC Drovandi, J McGree, AN Pettitt, A sequential monte carlo algorithm to incorporate model uncertainty in bayesian sequential design. J. Comput. Graphical Stat. 23(1), 3–24 (2014).
L Martino, J Read, V Elvira, F Louzada, Cooperative parallel particle filters for online model selection and applications to urban mobility. Digital Signal Process. 60:, 172–185 (2017).
CM Carvalho, MS Johannes, HF Lopes, NG Polson, Particle learning and smoothing. Statist. Sci. 25(1), 88–106 (2010).
C Andrier, A Doucet, R Holenstein, Particle markov chain monte carlo methods. JR Statist. Soc. B. 72(3), 269–342 (2010).
I Urteaga, MF Bugallo, PM Djuric, Sequential Monte Carlo methods under model uncertainty. IEEE Work. Stat. Sig. Process. Proc, 1–5 (2016). doi:10.1109/SSP.2016.7551747.
N Chopin, PE Jacob, O Papaspoliopoulos, Smc2: an efficient algorithm for sequential analysis of state-space models. JR Statist. Soc. B. 75:, 397–426 (2013).
P Bania, J Baranowski, in 2016 IEEE 55th Conference on Decision and Control (CDC). Field kalman filter and its approximation, (2016), pp. 2875–2880. doi:10.1109/CDC.2016.7798697.
ET Jaynes, Probability theory: the logic of science (Cambridge University Press, Cambridge, 2003).
Acknowledgements
We acknowledge this work under the scope of project titled ”PRONTO: PROcess NeTwork Optimization”. This project is financed by European commission’s HORIZON 2020 /Marie Skłodowska-Curie/ITN/EID grant agreement no: 675215.
Author information
Authors and Affiliations
Contributions
All the authors have participated in writing the manuscript and have revised the final version. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Baranowski, J., Bania, P., Prasad, I. et al. Bayesian fault detection and isolation using Field Kalman Filter. EURASIP J. Adv. Signal Process. 2017, 79 (2017). https://doi.org/10.1186/s13634-017-0514-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-017-0514-8
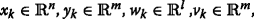 w
k
w
k
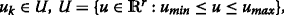 k=0,1,2,….
k=0,1,2,….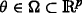 . The matrix functions A,B,G,C,V are of C
1 class w.r.t. both arguments and are of appropriate dimensions.
. The matrix functions A,B,G,C,V are of C
1 class w.r.t. both arguments and are of appropriate dimensions.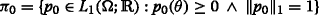 .
.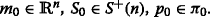
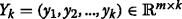 is a matrix of k first measurements.
is a matrix of k first measurements.






