- Research Article
- Open access
- Published:
Experiment Design Regularization-Based Hardware/Software Codesign for Real-Time Enhanced Imaging in Uncertain Remote Sensing Environment
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 254040 (2010)
Abstract
A new aggregated Hardware/Software (HW/SW) codesign approach to optimization of the digital signal processing techniques for enhanced imaging with real-world uncertain remote sensing (RS) data based on the concept of descriptive experiment design regularization (DEDR) is addressed. We consider the applications of the developed approach to typical single-look synthetic aperture radar (SAR) imaging systems operating in the real-world uncertain RS scenarios. The software design is aimed at the algorithmic-level decrease of the computational load of the large-scale SAR image enhancement tasks. The innovative algorithmic idea is to incorporate into the DEDR-optimized fixed-point iterative reconstruction/enhancement procedure the convex convergence enforcement regularization via constructing the proper multilevel projections onto convex sets (POCS) in the solution domain. The hardware design is performed via systolic array computing based on a Xilinx Field Programmable Gate Array (FPGA) XC4VSX35-10ff668 and is aimed at implementing the unified DEDR-POCS image enhancement/reconstruction procedures in a computationally efficient multi-level parallel fashion that meets the (near) real-time image processing requirements. Finally, we comment on the simulation results indicative of the significantly increased performance efficiency both in resolution enhancement and in computational complexity reduction metrics gained with the proposed aggregated HW/SW co-design approach.
1. Introduction
In this paper, we address a new aggregated Hardware/Software (HW/SW) codesign approach to optimization of the digital signal and image processing techniques as required for enhanced remote sensing (RS) of the environment with the use of high-resolution array radar and synthetic aperture radar (SAR) systems. At the algorithm-design level, the RS imaging problem is treated as an ill-posed nonlinear inverse problem of reconstruction of the spatial spectrum pattern (SSP) of the backscattered field distributed over the remotely sensed scene via processing the SAR data signals distorted in the uncertain stochastic measurement channel [1–6]. The operational scenario uncertainties are attributed to inevitable random signal perturbations in inhomogeneous propagation medium [1, 2, 4], possible imperfect radar/SAR system calibration [1, 3], and SAR carrier trajectory deviations [3, 5, 6]. The unified approach that we address to solve such a problem is based on the recently proposed concept of descriptive experiment design regularization (DEDR) [7, 8]. The general DEDR method constructed in [7, 8] incorporates into the minimum risk (MR) nonparametric estimation strategy [4] the experiment design-motivated constraints of the image identifiably for the discrete-form signal formation operator (SFO) specified by the employed signal modulation format [4–6]. On one hand, a considerable advantage of such DEDR paradigm relates to its flexibility in designing the desirable error metrics in the corresponding image representation space via defining different descriptive cost functions [7, 9]. On the other hand, the crucial limitations of the DEDR method relate to the necessity of performing simultaneously the solution-dependent SFO inversion operations and adaptive adjustments of the degrees of freedom of the overall DEDR image enhancement techniques ruled by the employed fixed-point iterative process [8]. For the real-world large-scale RS scenes, such adaptive full-format DEDR-optimal method turns out to be computationally extremely consuming, therefore cannot be recommended as a practical technique realizable in (near) real time [10]. The innovative idea of this paper is to aggregate the DEDR-optimal fixed-point iterative reconstruction/enhancement procedures developed in the previous studies [7, 8, 10] with the multi-level robustness and convergence enforcing regularization via constructing the proper projections onto convex sets (POCS) in the solution domain. The established POCS-regularized iterative DEDR technique is performed separately along the range and azimuth directions over the scene frame making an optimal use of the range-azimuth sparseness properties of the employed radar/SAR modulation format. Thus, at the SW codesign stage, we address two conceptually innovative propositions that distinguish our approach from the previous studies [7, 10]. First, two possible observation scenarios (instead of one) are unified now under the DEDR paradigm for the HW/SW codesign, namely, (i) regular case without model uncertaintiess and (ii) uncertain scenario with random perturbations in the SFO. Second, the POCS regularization is proposed to be performed in an aggregated multi-level fashion to make the optimal use of the non-trivial RS system model information for constructing the corresponding robustness and convergence enforcing POCS operators. In particular, the positivity and range-azimuth orthogonalization projectors of [10] are aggregated with the point spread function (PSF) sparseness enforcing sliding window projectors acting in parallel over both range and azimuth image frames that set the corresponding PSF pixel values to zeroes outside their specified support regions. Such aggregated POCS regularization drastically speeds up the resulting fixed-point iterative DEDR techniques making them exactly well fitted for the systolic computational implementation form; that is, provides the SW algorithmic base for the further HW codesign level of the problem treatment.
At the HW codesign stage, we propose to pursue the System-on-Chip (SoC) single Field Programmable (FP) unit integration approach [9–14], which allows efficient coupling/integration of a number of predetermined complex components. Such a programmable unit is a viable solution for rapid prototyping and digital implementation of the radar/SAR image enhancement techniques developed at the SW codesign stage, in spite of designing the process in a common personal computer (PC) [11–14]. The main advantage of the proposed FPSoC platform is that all required component designs, including the embedded processor unit, memory, and peripherals are algorithmically "adapted" for the particular developed POCS-regularized iterative fixed-point DEDR image enhancement techniques. Therefore, at the HW design stage, the novel contribution of this study is twofold: first, the addressed HW/SW codesign methodology is aimed at an HW implementation of the developed software using systolic arrays as coprocessors units; second, the proposed systolic-based processing architecture is particularly adapted for computational implementation of the unified DEDR-POCS techniques in a computationally efficient fashion that meets the (near) real-time overall RS imaging system requirements. We resume this study with the analysis of the simulation results related to enhancement of the real-world degraded large-scale SAR imagery (i.e., acquired in uncertain operational scenarios) indicative of the significantly increased reconstruction efficiency gained with the proposed HW/SW codesign approach.
2. Background
2.1. Continuous-Form Problem Model
The general formalism of the RS imaging problem presented in this paper is a structural extension of the problem considered in [4, 7, 8], hence some crucial model elements are repeated for convenience to the reader. Consider a coherent RS experiment in a random medium and the narrowband SAR assumption [1] that enables us to model the extended object backscattered wavefield in the baseband format [3] by imposing its time invariant complex scattering (backscattering) function  in the object image domain (scattering surface) X ∋ x. The measurement radar/SAR data field
in the object image domain (scattering surface) X ∋ x. The measurement radar/SAR data field  consists of the echo signals s and additive noise n and is available for observations and recordings within the prescribed time-space observation domain
consists of the echo signals s and additive noise n and is available for observations and recordings within the prescribed time-space observation domain  , where
, where  defines the time(t)-space(
defines the time(t)-space( ) points in Y;
) points in Y;  The model of the data field u is defined by specifying the stochastic equation of observation (EO) that in the conventional integral form may be written as [4, 8]
The model of the data field u is defined by specifying the stochastic equation of observation (EO) that in the conventional integral form may be written as [4, 8]

The random kernel  of the perturbed random signal formation operator (SFO)
of the perturbed random signal formation operator (SFO)  given by (1) defines the signal field formation model. Its mean
given by (1) defines the signal field formation model. Its mean  is referred to as the nominal modulation law in the data formation channel defined by the time-space modulation of signals employed in a particular imaging radar/SAR system [3], and the variation about the mean
is referred to as the nominal modulation law in the data formation channel defined by the time-space modulation of signals employed in a particular imaging radar/SAR system [3], and the variation about the mean  models the stochastic perturbations of the wavefield at different propagation paths, where
models the stochastic perturbations of the wavefield at different propagation paths, where  represents the zero-mean multiplicative noise that models random propagation perturbations in the medium (the so-called general Rytov model [3, 5, 6]). The fields
represents the zero-mean multiplicative noise that models random propagation perturbations in the medium (the so-called general Rytov model [3, 5, 6]). The fields  in (1) are assumed to be zero-mean complex valued Gaussian random fields [3]. Next, we assume an incoherent nature of the backscattered field
in (1) are assumed to be zero-mean complex valued Gaussian random fields [3]. Next, we assume an incoherent nature of the backscattered field  . This is naturally inherent to the RS experiments [1, 3, 5, 6] and leads to the
. This is naturally inherent to the RS experiments [1, 3, 5, 6] and leads to the  -form of the object field correlation function,
-form of the object field correlation function, 
 , where
, where  (x) and b(x)
(x) and b(x) 
 are referred to as the object random complex scattering function and its average power scattering function or spatial spectrum pattern (SSP), respectively.
are referred to as the object random complex scattering function and its average power scattering function or spatial spectrum pattern (SSP), respectively.
The problem of enhanced RS imaging is to develop a signal processing method for performing the efficient estimation of the SSP b(x) by processing the available radar/SAR measurements of the data wavefield u( y ). Such estimate  of the SSP b(x) is referred to as the desired reconstructed RS image of the remotely sensed scene.
of the SSP b(x) is referred to as the desired reconstructed RS image of the remotely sensed scene.
2.2. Discrete-Form Problem Model
Now we proceed from the stochastic integral-form EO (1) to its finite-dimensional discrete (vector) form approximation [8]

in which the disturbed SFO matrix

is the discrete-form approximation of the integral SFO  defined by the EO (1), and e, n, u represent zero-mean vectors composed of the decomposition (sampling) coefficients
defined by the EO (1), and e, n, u represent zero-mean vectors composed of the decomposition (sampling) coefficients 
 and
and  , respectively [7]. These vectors are characterized by the correlation matrices:R
e
, respectively [7]. These vectors are characterized by the correlation matrices:R
e
 D
D D(b)
D(b)  diag(b) (a diagonal matrix with vector b at its principal diagonal),
diag(b) (a diagonal matrix with vector b at its principal diagonal),  , and
, and 
 + R
n
, respectively, where
+ R
n
, respectively, where  defines the averaging performed over the randomness of
defines the averaging performed over the randomness of  characterized by the probability density function p(
characterized by the probability density function p( ) unknown to the observer, and superscript + stands for Hermitian conjugate (conjugate transpose). Vector b is composed of the elements b
k
) unknown to the observer, and superscript + stands for Hermitian conjugate (conjugate transpose). Vector b is composed of the elements b
k
 ; k
; k 1,
1, , K, and is referred to as a K-D vector-form representation of the SSP. The SSP vector b is associated with the so-called lexicographically ordered image pixels [7, 9]. The corresponding conventional K
y
, K, and is referred to as a K-D vector-form representation of the SSP. The SSP vector b is associated with the so-called lexicographically ordered image pixels [7, 9]. The corresponding conventional K
y
 K
x
rectangular frame-ordered scene image B
K
x
rectangular frame-ordered scene image B relates to its lexicographically ordered vector-form representation b
relates to its lexicographically ordered vector-form representation b  via the standard row by row expansion (so-called lexicographical reordering) procedure, B
via the standard row by row expansion (so-called lexicographical reordering) procedure, B L
L [9]. Note that in the simple case of a certain operational scenario [1, 3, 7], the discrete-form (i.e., matrix-form) SFO S is assumed to be deterministic, in which case the random perturbation term in (3) is irrelevant,
[9]. Note that in the simple case of a certain operational scenario [1, 3, 7], the discrete-form (i.e., matrix-form) SFO S is assumed to be deterministic, in which case the random perturbation term in (3) is irrelevant,  .
.
The digital enhanced RS imaging problem is formally stated as follows: to reconstruct the scene pixel frame image  via lexicographical reordering
via lexicographical reordering  L
L of the SSP vector estimate
of the SSP vector estimate  estimated from whatever available discrete measurements of the recorded radar/SAR data u. The reconstructed SSP vector
estimated from whatever available discrete measurements of the recorded radar/SAR data u. The reconstructed SSP vector  is an estimate of the second-order statistics of the scattering vector e observed through the perturbed SFO (3) contaminated with additive noise n and corrupted also with the signal-dependent multiplicative noise
is an estimate of the second-order statistics of the scattering vector e observed through the perturbed SFO (3) contaminated with additive noise n and corrupted also with the signal-dependent multiplicative noise , hence, the enhanced RS imaging problem at hand must be qualified and treated as a statistical nonlinear inverse problem with model uncertainties. The high-resolution sensing implies formation of the RS image
, hence, the enhanced RS imaging problem at hand must be qualified and treated as a statistical nonlinear inverse problem with model uncertainties. The high-resolution sensing implies formation of the RS image  based on some statistically optimal solution of such an inverse problem robust against the problem model uncertainties. In this paper we propose to unify the POCS regularization with the DEDR method originally developed in [7, 8].
based on some statistically optimal solution of such an inverse problem robust against the problem model uncertainties. In this paper we propose to unify the POCS regularization with the DEDR method originally developed in [7, 8].
3. Unified DEDR Method
3.1. DEDR Strategy for Certain Operational Scenario
In the descriptive statistical formalism, the desired SSP vector  is recognized to be the vector of a principal diagonal of the estimate of the correlation matrix R
e
(b); that is,
is recognized to be the vector of a principal diagonal of the estimate of the correlation matrix R
e
(b); that is, 
 . Thus one can seek to estimate
. Thus one can seek to estimate 
 given the data correlation matrix R
u
preestimated empirically via averaging
given the data correlation matrix R
u
preestimated empirically via averaging  recorded data vector snapshots
recorded data vector snapshots  ; for example, [7]
; for example, [7]

by determining the solution operator (SO) F such that

where  defines the vector composed of the principal diagonal of the embraced matrix.
defines the vector composed of the principal diagonal of the embraced matrix.
To optimize the search for F in the certain operational scenario, the DEDR strategy was proposed in [7] as


that implies the minimization of the weighted sum of the systematic and fluctuation errors in the desired estimate  where the selection (adjustment) of the regularization parameter
where the selection (adjustment) of the regularization parameter  and the weight matrix A provide the additional experiment design degrees of freedom incorporating any descriptive properties of a solution if those are known a priori [3, 7]. It is easy to recognize that the strategy (6) is a structural extension of the statistical minimum risk estimation strategy [4] for the nonlinear spectral estimation problem at hand because in both cases the balance between the gained spatial resolution and the noise suppression in the resulting estimate is to be optimized.
and the weight matrix A provide the additional experiment design degrees of freedom incorporating any descriptive properties of a solution if those are known a priori [3, 7]. It is easy to recognize that the strategy (6) is a structural extension of the statistical minimum risk estimation strategy [4] for the nonlinear spectral estimation problem at hand because in both cases the balance between the gained spatial resolution and the noise suppression in the resulting estimate is to be optimized.
3.2. Extended DEDR Strategy for Uncertain Scenario
To optimize the search for the desired SO F in the uncertain operational scenario with the randomly perturbed SFO (3), the extended DEDR strategy was proposed in [8] as


where the conditioning term (9) represents the worst-case statistical performance (WCSP) regularizing constraint imposed on the unknown second-order statistics  of the random distortion component
of the random distortion component  of the SFO matrix (3), and the DEDR "extended risk" is defined by
of the SFO matrix (3), and the DEDR "extended risk" is defined by

where the regularization parameter  and the metrics inducing weight matrix A compose the processing level "degrees of freedom" of the DEDR method.
and the metrics inducing weight matrix A compose the processing level "degrees of freedom" of the DEDR method.
To proceed with the derivation of the robust SO (8), in [8], the risk function (10) was next decomposed and evaluated for its the maximum value applying the Cauchy-Schwarz inequality and Loewner ordering [9] of the weight matrix  with the scaled Loewner ordering factor
with the scaled Loewner ordering factor  min
min . With these robustifications [8], the extended DEDR strategy (8) is transformed into the following optimization problem:
. With these robustifications [8], the extended DEDR strategy (8) is transformed into the following optimization problem:

with the aggregated DEDR risk function [8]

where

3.3. DEDR-Optimal Solution Operators
Examining the DEDR strategies (6) and (11) one can deduce that those both are structurally similar and differ only by the definition of the second (i.e., noise) risk component terms in (7) and (12). In the certain operational scenario [5–7], the trace  for the noise error measure is used, while in the uncertain scenario [8] the augmented measure tr
for the noise error measure is used, while in the uncertain scenario [8] the augmented measure tr is employed with the diagonal loaded extension (13) of the composite noise correlation matrix
is employed with the diagonal loaded extension (13) of the composite noise correlation matrix  . The established structural similarity (the so-called problem model homomorphism [5, 6]) of two DEDR problems (6) and (11) makes it possible to unify the solutions for both scenarios. Doing so, we specify the SOs for both considered operational scenarios, namely:
. The established structural similarity (the so-called problem model homomorphism [5, 6]) of two DEDR problems (6) and (11) makes it possible to unify the solutions for both scenarios. Doing so, we specify the SOs for both considered operational scenarios, namely:
-
(1)
SO for certain operational scenario follows directly from the solution to the optimization problem (6) found in the previous study [7] that results in
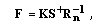 (14)
(14)where
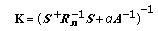 (15)
(15)represents the so-called regularized reconstruction operator [7];
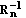 is the noise whitening filter, and the adjoint (i.e., Hermitian transpose) SFO
is the noise whitening filter, and the adjoint (i.e., Hermitian transpose) SFO  defines the matched spatial filter in the conventional signal processing terminology [1, 3];
defines the matched spatial filter in the conventional signal processing terminology [1, 3]; -
(2)
SO for uncertain operational scenario follows as structural extension of (14) for the augmented (diagonal loaded)
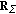 that yields [8]
that yields [8] (16)
(16)where
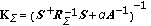 (17)
(17)represents the robustified reconstruction operator for the uncertain scenario.
3.4. DEDR-Related Imaging Techniques
Here we exemplify three practically motivated DEDR-related imaging techniques [7, 8], that will be used at the HW codesign stage, namely, the conventional matched spatial filtering (MSF) method, and two high-resolution reconstructive imaging techniques: (i) the robust spatial filtering (RSF), and (ii) the robust adaptive spatial filtering (RASF) methods.
-
(1)
MSF. The MSF algorithm is a member of the DEDR-related family [7] specified for
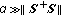 , that is, the case of a dominating priority of suppression of noise over the systematic error in the optimization problem (6). In this case, the SO (14) is approximated by the matched spatial filter (MSF) [7]:
, that is, the case of a dominating priority of suppression of noise over the systematic error in the optimization problem (6). In this case, the SO (14) is approximated by the matched spatial filter (MSF) [7]: (18)
(18) -
(2)
RSF. The RSF method implies no preference to any prior model information (i.e.,
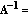 I) and balanced minimization of the systematic and noise error measures in (9), (11) by adjusting the regularization parameter
I) and balanced minimization of the systematic and noise error measures in (9), (11) by adjusting the regularization parameter  to the inverse of the signal-to-noise ratio (SNR). In that case the SO becomes the Tikhonov-type robust spatial filter (RSF) [7]:
to the inverse of the signal-to-noise ratio (SNR). In that case the SO becomes the Tikhonov-type robust spatial filter (RSF) [7]: (19)
(19)in which the RSF regularization parameter
 RSF
is adjusted to a particular operational scenario model, namely,
RSF
is adjusted to a particular operational scenario model, namely, 
 (
(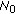 /
/ ) for the case of a certain operational scenario [7], and
) for the case of a certain operational scenario [7], and 
 (
(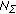 /
/ ) in the uncertain operational scenario case [8], respectively, where
) in the uncertain operational scenario case [8], respectively, where 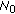 represents the white observation noise power density,
represents the white observation noise power density, 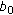 is the average a priori SSP value, and
is the average a priori SSP value, and 

 +
+ 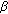 corresponds to the augmented noise power density in the correlation matrix specified by (13).
corresponds to the augmented noise power density in the correlation matrix specified by (13). -
(3)
RASF. In the Bayesian statistically optimal problem treatment,
 and A are adjusted in an adaptive fashion following the Bayesian minimum risk strategy [8], that is,
and A are adjusted in an adaptive fashion following the Bayesian minimum risk strategy [8], that is, 
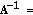
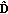
 diag(
diag( ), the diagonal matrix with the estimate
), the diagonal matrix with the estimate  at its principal diagonal, in which case the SOs (14), (16) become itself solution-dependent operators that result in the following robust adaptive spatial filters (RASFs):
at its principal diagonal, in which case the SOs (14), (16) become itself solution-dependent operators that result in the following robust adaptive spatial filters (RASFs): (20)
(20)for the certain operational scenario [7], and
 (21)
(21)for the uncertain operational scenario [8], respectively. Next, in all practical RS scenarios [1–3] (and specifically, in SAR uncertain imaging applications [2, 7, 8]), it is a common practice to accept the robust white additive noise model, that is,
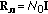 , attributing the unknown correlated noise component as well as multiplicative speckle noise to the composite uncertain noise term
, attributing the unknown correlated noise component as well as multiplicative speckle noise to the composite uncertain noise term 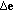 in (2), in which case
in (2), in which case 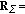
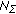 I with the composite noise power density
I with the composite noise power density 


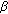 , the initial observation noise variance
, the initial observation noise variance 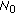 augmented by the loading factor
augmented by the loading factor 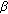 specified by (13).
specified by (13).
Using the defined above SOs, the DEDR-related data processing techniques in the conventional pixel-frame format can be unified now as follows:

with  =
=  ;
; 

 , and
, and 

 ,
, 
 , respectively. Any other feasible adjustments of the DEDR degrees of freedom (the regularization parameters
, respectively. Any other feasible adjustments of the DEDR degrees of freedom (the regularization parameters  ,
,  , and the weight matrix A) provide other possible DEDR-related SSP reconstruction techniques, that we do not consider in this paper.
, and the weight matrix A) provide other possible DEDR-related SSP reconstruction techniques, that we do not consider in this paper.
4. POCS Regularized DEDR Method
Because of the extremely high dimension 
 1012 of the operator inversions required to form the corresponding SOs specified by (20), (21), it is questionable to recommend the general-form DEDR-optimal method (22) as a practical enhanced RS imaging technique realizable in (near) real computational time. Hence, one has to proceed from the conventional-form
1012 of the operator inversions required to form the corresponding SOs specified by (20), (21), it is questionable to recommend the general-form DEDR-optimal method (22) as a practical enhanced RS imaging technique realizable in (near) real computational time. Hence, one has to proceed from the conventional-form  -dimensional RSF and RASF algorithms (that require cumbersome operator inversions (20)–(22) to more computationally efficient iterative techniques that do not involve the large-scale operator inversions and incorporate the convergence enforcement regularization into the DEDR procedure via constructing the proper projections onto convex sets (POCS) in the solution domain. In the considered here RS imaging applications, such POCS is aimed at performing the factorization of the overall procedures over the orthogonal range (y)-azimuth (x) coordinates in the scene frame making also an optimal use of the sparseness properties of the employed radar/SAR modulation format. Thus, the innovative idea is to perform the POCS regularization in an aggregated multi-level fashion. In particular, we propose to aggregate the positivity and range-azimuth orthogonalization projectors constructed previously in [10] with the point spread function (PSF) sparseness enforcing sliding window projectors acting in parallel over both range and azimuth image frames that set the corresponding PSF pixel values to zeroes outside their specified support regions. In this section, we address such a unified multi-level POCS-regularized iterative DEDR method as an extension of the previously proposed single-level DEDR-POCS [10] that we develop here in two stages.
-dimensional RSF and RASF algorithms (that require cumbersome operator inversions (20)–(22) to more computationally efficient iterative techniques that do not involve the large-scale operator inversions and incorporate the convergence enforcement regularization into the DEDR procedure via constructing the proper projections onto convex sets (POCS) in the solution domain. In the considered here RS imaging applications, such POCS is aimed at performing the factorization of the overall procedures over the orthogonal range (y)-azimuth (x) coordinates in the scene frame making also an optimal use of the sparseness properties of the employed radar/SAR modulation format. Thus, the innovative idea is to perform the POCS regularization in an aggregated multi-level fashion. In particular, we propose to aggregate the positivity and range-azimuth orthogonalization projectors constructed previously in [10] with the point spread function (PSF) sparseness enforcing sliding window projectors acting in parallel over both range and azimuth image frames that set the corresponding PSF pixel values to zeroes outside their specified support regions. In this section, we address such a unified multi-level POCS-regularized iterative DEDR method as an extension of the previously proposed single-level DEDR-POCS [10] that we develop here in two stages.
4.1. First Stage: Fixed-Point Iterative DEDR Algorithm
The first stage is a structural extension of the fixed-point method considered in [10], the extension being done for the case of the unified SOs specified now by (14) and (16). Thus, following the fixed-point algorithm design scheme of [10, Section 3], we first, specify a sequence of the iterative DEDR-POCS estimates

 where
where  is a convergence enforcing projector (i.e., the POCS-regularizing operator) that will be construct at the second design stage (in the next subsection). In (23),
is a convergence enforcing projector (i.e., the POCS-regularizing operator) that will be construct at the second design stage (in the next subsection). In (23),

represents the self-adjoint reconstruction operator at the i th iteration step,  and
and

is the nominal system point spread function (PSF) operator (a  matrix). Applying routinely the fixed-point technique [9, 10] to (23), we derive the desired extended POCS-regularized iterative SSP estimation algorithm
matrix). Applying routinely the fixed-point technique [9, 10] to (23), we derive the desired extended POCS-regularized iterative SSP estimation algorithm

Here,

represents the solution-dependent matrix-form iteration operator, in which


 denotes the Shur-Hadamar (element-by-element) matrix product, and the zero-step iteration
denotes the Shur-Hadamar (element-by-element) matrix product, and the zero-step iteration

is formed as an outcome of the MSF algorithm from the DEDR family (22) specified for the adjoint SFO solution operator  .
.
4.2. B. Second Stage: Multilevel POCS Regularization
Next, to specify the regularizing POCS projector operator  in the fixed-point algorithm (26) let us make the use of factorization of the PSM (25) over the azimuth (x) and range (y) coordinates valid for all existing imaging radar/SAR systems [2, 3, 9]. Such factorization is illustrated in Figure 1. We formalize this stage by introducing the range-azimuth factorization operator
in the fixed-point algorithm (26) let us make the use of factorization of the PSM (25) over the azimuth (x) and range (y) coordinates valid for all existing imaging radar/SAR systems [2, 3, 9]. Such factorization is illustrated in Figure 1. We formalize this stage by introducing the range-azimuth factorization operator  , the same one as in the previous POCS regularization considered in [10]. Next, to make a use of the intrinsic sparseness properties of the SAR point spread functions over the range and azimuth frames, we propose to incorporate the new POCS regularization stage via constructing the x-y factorized projection operator (algorithm)
, the same one as in the previous POCS regularization considered in [10]. Next, to make a use of the intrinsic sparseness properties of the SAR point spread functions over the range and azimuth frames, we propose to incorporate the new POCS regularization stage via constructing the x-y factorized projection operator (algorithm) that acts as a composition of the orthogonal sliding windows [9] with the window apertures adjusted to the PSM widths: (i) 2
that acts as a composition of the orthogonal sliding windows [9] with the window apertures adjusted to the PSM widths: (i) 2 a
specifies the azimuth window frame adjusted to the effective pixel width of the non-zero strip
a
specifies the azimuth window frame adjusted to the effective pixel width of the non-zero strip  a
(x) of the azimuth PSM
a
(x) of the azimuth PSM  a
along the x axis; (ii) 2
a
along the x axis; (ii) 2 r
specifies the range window frame adjusted to the effective pixel width of the non-zero strip
r
specifies the range window frame adjusted to the effective pixel width of the non-zero strip  of the range PSM
of the range PSM along the y axis, respectively, as illustrated in Figure 1. Such the sliding window projector
along the y axis, respectively, as illustrated in Figure 1. Such the sliding window projector  is an easy-to-implement numerical algorithm [9] that simply sets the pixels values to zero outside the support regions 2
is an easy-to-implement numerical algorithm [9] that simply sets the pixels values to zero outside the support regions 2 a
a
 K
x
and 2
K
x
and 2 r
r
 K
y
around every particular pixel
K
y
around every particular pixel  ; k
x
; k
x

 ; k
v
; k
v
 in the rectangular image frame
in the rectangular image frame  L
L separately reconstructed via (26) along the corresponding x and y axes, respectively. Last, following [10], to enforce prior knowledge on the intrinsic positivity of the SSP we impose, in addition to
separately reconstructed via (26) along the corresponding x and y axes, respectively. Last, following [10], to enforce prior knowledge on the intrinsic positivity of the SSP we impose, in addition to  and
and  , the positivity operator (algorithm)
, the positivity operator (algorithm)  that has the effect of clipping off all negative values [8]. The defined above orthogonal projecting window
that has the effect of clipping off all negative values [8]. The defined above orthogonal projecting window  and positivity operator
and positivity operator  are projectors onto convex sets, that is POCS operators [9], thus a composition
are projectors onto convex sets, that is POCS operators [9], thus a composition

is a POCS operator as well. While this definition in the terms of the proposed aggregated projections sounds complicated, the algorithmic meaning of (31) is very simple and is easily established in the algorithmic form familiar to the signal processing and RS communities. Acting on a  (that may be not a member of the convex set at a particular iteration
(that may be not a member of the convex set at a particular iteration  ), the
), the  applied to
applied to  produces the member of the convex cone set composed of non-negative elements that is nearest to
produces the member of the convex cone set composed of non-negative elements that is nearest to  in the sense of minimization of the
in the sense of minimization of the  norm
norm  [9, Section
[9, Section  ].
].
Now, the application of the  constructed by (31) to the iteration process (26) with the corresponding lexicographical reordering
constructed by (31) to the iteration process (26) with the corresponding lexicographical reordering  L
L yields the desired resulting POCS-regularized fixed point update rule
yields the desired resulting POCS-regularized fixed point update rule

in which the zero-step iteration  L
L is formed using the conventional (i.e., low-resolution) MSF imaging algorithm (30), the aggregated convergence enforcing POCS regularizing operator is constructed by (31), and the matrix-form fixed-point iteration operator
is formed using the conventional (i.e., low-resolution) MSF imaging algorithm (30), the aggregated convergence enforcing POCS regularizing operator is constructed by (31), and the matrix-form fixed-point iteration operator  is specified by (27).
is specified by (27).
We address such POCS-regularized DEDR technique (32) as the unified DEDR-POCS method. Its general framework is presented in Figure 2. Note that the fixed-point process (32) does not involve the cumbersome operator inversions (in contrast to the initial DEDR techniques defined by (5), (22) and, moreover, it is performed separately along the range (y) and azimuth (x) directions making an optimal use of the PSM sparseness properties  . These features of the POCS-regularized RSF and RASF algorithms generalized by (32) result in the drastically decreased algorithmic computational complexity (e.g,
. These features of the POCS-regularized RSF and RASF algorithms generalized by (32) result in the drastically decreased algorithmic computational complexity (e.g,  ~ 103
~ 103 104 times at each iteration for the typical large-scale SAR image formats [1, 2]) that we will verify and analyze in more details further on in Section 6.
104 times at each iteration for the typical large-scale SAR image formats [1, 2]) that we will verify and analyze in more details further on in Section 6.
4.3. DEDR-POCS Convergence
We accomplish our algorithmic developments at the SW codesign stage with the analytical analysis of the convergence issues related to the developed unified DEDR-POCS method. Following the POCS regularization formalism [9], the convergence enforcing projectors in the iterated procedure (32) are to be constructed formally as

where  1, 2, 3 represent the relaxation (speeding-up) regularization parameters and
1, 2, 3 represent the relaxation (speeding-up) regularization parameters and  is the identity operator. The iteration rule (32) for the composed regularizing projectors (33) becomes
is the identity operator. The iteration rule (32) for the composed regularizing projectors (33) becomes

and is guaranteed to converge to the point in the intersection of the convex sets specified by  provided
provided  for all
for all  1, 2, 3 regardless of the initialization
1, 2, 3 regardless of the initialization  that is a direct sequence of the fundamental theorem of POCS [9, page 1066]. Note that the employed specifications of the projectors in (33), that is,
that is a direct sequence of the fundamental theorem of POCS [9, page 1066]. Note that the employed specifications of the projectors in (33), that is, 

 ;
;  ;
; 
 ; with
; with  1 for all
1 for all  and
and  L
L , satisfy these POCS convergence conditions, in which case the formal convergent POCS procedure (34) becomes the developed above fixed-point DEDR-POCS algorithm given by (32).
, satisfy these POCS convergence conditions, in which case the formal convergent POCS procedure (34) becomes the developed above fixed-point DEDR-POCS algorithm given by (32).
Now we are ready to proceed with the hardware codesign implementation stage of our development.
5. Hardware/Software Codesign Methodology
The all-software execution of the prescribed RS image formation and reconstruction operations in modern high-speed personal computers (PC) or any existing digital signal processors (DSP) may be intensively time consuming [15]. These high computational complexities of the general-form DEDR-POCS algorithms make them definitely unacceptable for real time PC-aided implementation.
When a coprocessor-based solution is employed in the HW/SW codesign architecture, the computational time can be drastically reduced [16]. As an introductive example, consider computation of the matrix product AB, where A and B define matrices of sizes k m and m
m and m p, respectively. Then to execute this product in a conventional sequential way, k
p, respectively. Then to execute this product in a conventional sequential way, k m
m p multiply accumulation (MAC) operations are required. Therefore, the computational time required by a sequential processor or a high-speed PC for the all-software execution of the matrix product is of the order
p multiply accumulation (MAC) operations are required. Therefore, the computational time required by a sequential processor or a high-speed PC for the all-software execution of the matrix product is of the order  With the incorporation of a parallel and/or pipelined coprocessor alongside an embedded processor the required computational time is immediately reduced to O(
With the incorporation of a parallel and/or pipelined coprocessor alongside an embedded processor the required computational time is immediately reduced to O( where n defines the employed parallelism level.
where n defines the employed parallelism level.
In this section, we present a concise description of the proposed HW/SW codesign approach particularly adapted to the DEDR-POCS type algorithms, and demonstrate its flexibility in performing an efficient HW implementation of the SW processing tasks with systolic arrays as coprocessors units. In [10], we presented an initial version of the HW/SW-architecture for implementing the digital processing of a large-scale RS imagery in other operational context. The architecture developed in [10] did not involve systolic arrays and is considered here simply as a reference for the new pursued HW/SW codesign paradigm presented in Figure 3, where the corresponding blocks are to be designed to speed-up the digital signal processing operations of the DEDR-POCS-related algorithms developed at the previous SW stage of the overall HW/SW to meet the real time imaging system requirements. Our codesign methodology encompasses the following general stages: (i) algorithmic implementation (reference simulation in the MATLAB platform); (ii) computational tasks partitioning process (definition of the number of coprocessors), and (iii) operational mapping process employed to map the computation execution tasks onto the HW blocks (reconfigurable arrays).
In the HW design, we use the precision of 32 bits for performing all fixed-point operations, in particular, 9-bit integer and 23-bits decimal for the implementation of each coprocessor. Such the precision guarantees numerical computational errors less than 105 referring to the MATLAB Fixed Point Toolbox [17]. Using such the MATLAB fixed-point toolbox we generated all the numerical test sequences required to verify computationally the proposed HW/SW codesign methodology (i.e., test sequences for performing the SW simulation and for the HW verifications). The results of such SW simulation and HW performance analysis will be presented and discussed further on in Sections 6.3 and 6.4. Finally, the host processor (the standard MicroBlaze embedded processor [18] in this study) performs the following functions: loading and storing of images, data transfer to the HW coprocessors, and data formatting for performing the correspondent mathematical operations.
5.1. Algorithmic Implementation
In this section, we develop the procedures for computational implementation of the DEDR-POCS-related RSF and RASF algorithms in the MATLAB platform. This reference implementation scheme will be next compared with the proposed HW/SW codesign architecture based on the use of the single Field Programmable Gate Array chip.
To implement the iterative fixed-point DEDR-POCS-related RSF and RASF algorithms (32), we first, specify the corresponding computational procedures in the rectangular scene frame r ∈ over the azimuth (horizontal axis, x) and range direction (vertical axis, y), respectively. Such multi-stage procedures are formalized via the unified algorithmic scheme presented in Table 1.
∈ over the azimuth (horizontal axis, x) and range direction (vertical axis, y), respectively. Such multi-stage procedures are formalized via the unified algorithmic scheme presented in Table 1.
From the analysis of the algorithmic implementation scheme of Table 1, we outline the following important remarks regarding the possible HW/SW partitioning of the computational tasks required for implementing both RSF and RASF algorithms.
-
(i)
First, the PSMs (25),
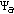 and
and  factorized over the azimuth and range axes can be calculated concurrently that we refer to as
factorized over the azimuth and range axes can be calculated concurrently that we refer to as 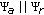 , where symbol
, where symbol  specifies now the concurrent execution of the corresponding computational operations.
specifies now the concurrent execution of the corresponding computational operations. -
(ii)
Second, the zero step iteration (MSF image)
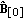 can be computed using the same factorized structure analogues to
can be computed using the same factorized structure analogues to 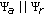 .
. -
(iii)
Third, the reconstructed image
 , at the current (i
, at the current (i 1)st iteration step is an iteratively updated function of
1)st iteration step is an iteratively updated function of 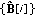 computed at the previous i th iteration that also admits the factorized computing.
computed at the previous i th iteration that also admits the factorized computing.
5.2. Partitioning Phase
One of the challenging problems of the HW/SW codesign is to perform an efficient HW/SW partitioning of the computational tasks. The goal of the partitioning stage is to find which computational tasks can be implemented in an efficient parallelized HW/SW architecture seeking for balanced area-time trade-offs between different admissible design solutions [18–20]. In this study, the iterative fixed-point POCS-DEDR regularized algorithm has been partitioned at the algorithmic level to minimize the overall signal processing (SP) time via transferring some required reconstructive SP functions from the SW to the HW. The solution to this problem requires, first, the definition of a partitioning model that meets all the specification requirements (functionality, goals and constraints).
The system partitioning is clearly influenced by the target architecture onto which the HW and the SW will be mapped. The target architecture proposed in this study consists of one 32 bits RISC instruction set embedded processor (MicroBlaze) running the software and three dedicated coprocessors implemented by systolic processor arrays.
We begin with the specifications of the system-level partitioning functions and detailing the selected design quality attributes for the HW/SW codesign aimed at the definition of the computational tasks that can be implemented in a systolic computing form, namely: hardware area (ha), hardware execution time (ht), software execution time (St), and the selected system resolution (n); where maxha, maxht and maxSt represent the upper bounds of these constraints. In particular, for implementing the iterative fixed-point POCS-regularized RSF and RASF algorithms, the partitioning process must satisfy the following performance requirements.
-
(i)
In order to ensure a viable solution, the system must always satisfy the constraints:
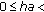 max ha,
max ha, 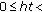 max ht, for each i th hardware coprocessor
max ht, for each i th hardware coprocessor  and
and  max St, for the embedded processor
max St, for the embedded processor  . These three hardware coprocessors
. These three hardware coprocessors  and the embedded processor compose the target architecture
and the embedded processor compose the target architecture  , for the pre-selected FPGA
, for the pre-selected FPGA  with the corresponding pre-determined architecture constraints
with the corresponding pre-determined architecture constraints 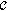 :
: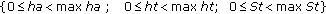 [18].
[18]. -
(ii)
Each block implementation
 must satisfy the predefined execution time performance requirements [18]:
must satisfy the predefined execution time performance requirements [18]: 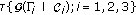 and
and 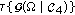 conditioned by the specified above architecture constraints
conditioned by the specified above architecture constraints 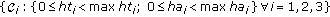 , and
, and 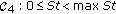 , correspondingly.
, correspondingly.
Next, the system architecture  is to be specified to meet the desirable time consuming performances via bounding the total expected system processing time
is to be specified to meet the desirable time consuming performances via bounding the total expected system processing time  evaluated by
evaluated by

where  represents the execution time required for implementing the corresponding DEDR-POCS-related RSF and RASF algorithms in the standard MATLAB computational environment.
represents the execution time required for implementing the corresponding DEDR-POCS-related RSF and RASF algorithms in the standard MATLAB computational environment.
Following such partitioning paradigm, we decompose now the fixed-point POCS-regularized RSF and RASF algorithms developed at the SW-design into the standard MicroBlaze embedded processor  with three coprocessors
with three coprocessors  as illustrated in Figure 4. The first coprocessor
as illustrated in Figure 4. The first coprocessor  (referred to as MSF coprocessor) implements the zero-step iteration to form the MSF image
(referred to as MSF coprocessor) implements the zero-step iteration to form the MSF image  specified by (30). The second coprocessor
specified by (30). The second coprocessor  (referred to as PSM coprocessor) implements the computations of the PSM
(referred to as PSM coprocessor) implements the computations of the PSM  given by (25) concurrently over the azimuth and the range directions. The third coprocessor
given by (25) concurrently over the azimuth and the range directions. The third coprocessor  (referred to as Iterative POCS coprocessor) performs the required robust updating
(referred to as Iterative POCS coprocessor) performs the required robust updating 

 (
( ) for implementing the RSF algorithm and the adaptive updating
) for implementing the RSF algorithm and the adaptive updating 

 (
( ) for implementing the POCS-regularized RASF image reconstruction algorithm, respectively. All three coprocessors
) for implementing the POCS-regularized RASF image reconstruction algorithm, respectively. All three coprocessors  are next implemented as systolic processor arrays while the embedded processor
are next implemented as systolic processor arrays while the embedded processor  executes all the required operational and control functions: loading and storing of the images, data transfer to the HW coprocessors, and data formatting for execution of all required numerical operations.
executes all the required operational and control functions: loading and storing of the images, data transfer to the HW coprocessors, and data formatting for execution of all required numerical operations.
5.3. Mapping Phase
In this section, we proceed with the development of the procedure for mapping the corresponding algorithms onto array processors. A systolic array consists of a number of processor elements (PEs) with the corresponding interconnection links among the PEs, and the mapping technique transforms a space representation into a space-time representation [21]. Systolic arrays are being used for matrix operations and required specific processing algorithms, such as, transform techniques, matrix multiplication, convolution, and so forth, [21, 22]. The methodology of mapping the algorithms onto array structures is depicted in Figure 5.
First, to achieve the desired maximal possible parallelism in an algorithm, we perform the analysis of the data dependencies in the corresponding computations. Then, the algorithm is transformed into a single assignment algorithm without global communication. A dependence graph (DG) is used to analyze these data dependencies of the corresponding algorithms [21]. Following [21], DG is defined as  , where P represents a set of nodes and E is a set of arcs (or edges), that is, each edge
, where P represents a set of nodes and E is a set of arcs (or edges), that is, each edge  connects the corresponding pair of nodes
connects the corresponding pair of nodes  and the connection is formalized by
and the connection is formalized by  .
.
Second, we employ the systolic design paradigm to map a high dimensional (N- dimensional) DG to a lower dimensional Signal to Flow Graph (SFG) [21]. Recall that the systolic array is a space-time representation, in which the function description defines the behavior within a node, whereas the structural description specifies the interconnections (edges and delays) between the nodes [21, 22]. In order to derive a regular systolic array architecture with minimum number of nodes, we employ the linear projection approach for processor assignment following the methodology developed in [21, 22], that is, the nodes of the DG in a certain straight line are projected onto the corresponding PEs in the processor array represented by the corresponding projection vector  . Thus, we seek for a linear order reduction transformation [22]:
. Thus, we seek for a linear order reduction transformation [22]:

that maps the N-dimensional DG (GN) onto the (N– 1)-dimensional SFG ( ).
).
Such the desired linear transformation matrix  admits the partitioning in two functions [22]
admits the partitioning in two functions [22]

Here,  defines a (1
defines a (1 p) vector composed of the first row of
p) vector composed of the first row of  that determines the time scheduling. This vector indicates the normal direction of the equi-temporal hyper-planes in the DG, "equi-temporal" being understood in the sense that all the nodes on the same hyper-plane must be processed at the same time [22]. The submatrix
that determines the time scheduling. This vector indicates the normal direction of the equi-temporal hyper-planes in the DG, "equi-temporal" being understood in the sense that all the nodes on the same hyper-plane must be processed at the same time [22]. The submatrix  of
of  dimension (the rest rows of
dimension (the rest rows of  ), determine the space processor. With this mapping, we are now ready to proceed with the construction of the required regular (N – 1)-dimensional systolic arrays.
), determine the space processor. With this mapping, we are now ready to proceed with the construction of the required regular (N – 1)-dimensional systolic arrays.
5.4. HW Implementation
Once the HW/SW codesign has been defined, the three coprocessors employed in the architecture exemplified in Figure 4 can be implemented using the HW systolic arrays. In this study, we are oriented at the use of the Xilinx MicroBlaze soft processor that employs the On Chip Peripheral Bus (OPB) for transferring the data from/to the memory to/from the coprocessor [23]. Such the OPB is a fully synchronous bus that connects other separate 32 bit data buses. This system architecture (based on the FPGA XC4VSX35-10ff668 with the embedded processor and the OPB buses) restricts the corresponding processing frequency to 100 MHz. The typical rate of the OPB bus is 133 MByte/s, providing that each data transfer of 32-bits is accomplished at 30.05 ns [23]. Next, to avoid multiple data transfer from the embedded processor data memory to the coprocessors, a register file is to be implemented inside each coprocessor.
The first systolic array (referred to as the MSF coprocessor) implements the zero-step iteration of the unified fixed-point DEDR-POCS procedure (32) to form the MSF image  as specified by (30). The function of this systolic array is to perform the triple matrix multiplication, where matrix S has the band-Toeplitz structure [5, 6] with the width of the non-zero strip over the azimuth frame equal to
as specified by (30). The function of this systolic array is to perform the triple matrix multiplication, where matrix S has the band-Toeplitz structure [5, 6] with the width of the non-zero strip over the azimuth frame equal to  Following the methodology addressed in the previous section, the triple matrix multiplication corresponding to the MSF function can be implemented using a cascade systolic array. First, the multiplication of a band-Toeplitz matrix and a rectangular matrix is performed and then, the result is multiplied with another band-Toeplitz matrix. Each slide of the DG in the multiplication of the band-Toeplitz matrix and the rectangular matrix is employed using the following specifications in the transformations defined by (37):
Following the methodology addressed in the previous section, the triple matrix multiplication corresponding to the MSF function can be implemented using a cascade systolic array. First, the multiplication of a band-Toeplitz matrix and a rectangular matrix is performed and then, the result is multiplied with another band-Toeplitz matrix. Each slide of the DG in the multiplication of the band-Toeplitz matrix and the rectangular matrix is employed using the following specifications in the transformations defined by (37):  for the vector schedule,
for the vector schedule,  for the projection vector and
for the projection vector and  for the space processor that determine the resulting transformation matrix
for the space processor that determine the resulting transformation matrix  (37). In Figure 6(a), we illustrate the triple matrix multiplication mapped into a cascade systolic array with the relevant MSF systolic array architecture exemplified in Figure 6(b). The corresponding computations require only O(
(37). In Figure 6(a), we illustrate the triple matrix multiplication mapped into a cascade systolic array with the relevant MSF systolic array architecture exemplified in Figure 6(b). The corresponding computations require only O( ) fixed-point operations, with
) fixed-point operations, with  where, as previously, 2
where, as previously, 2 a
defines the width of the non-zero strip in the factorized band-Toeplitz PSM (25) and
a
defines the width of the non-zero strip in the factorized band-Toeplitz PSM (25) and  is the original image dimension over the azimuth frame.
is the original image dimension over the azimuth frame.
The MSF coprocessor systolic architecture of Figure 6(b) consists of identical linearly-connected processing elements (PEs). In our case, the internal structure of each PE contains a multiplier and an adder. Each PE receives 32-bits operands and generates 64-bits product. Then, the product is truncated to 32-bits with a fixed-point adopted representation of 9 integers and 24 decimals. Next, since the band-Toeplitz type matrix S
a
is preloaded, the incoming data  are transmitted in parallel to the corresponding PEs. After 2
are transmitted in parallel to the corresponding PEs. After 2 cycles of clock, the data outputs are produced and transferred to the registers (gray blocks in Figure 6(a)). Once the first of the triple matricial product is completed, the data transfer to the second array begins. The control unit block guarantees the correct synchronization between the arrival of the input data and the computations for each PE. The result buffer of Figure 6(b) consists of a shift buffer used to store the
cycles of clock, the data outputs are produced and transferred to the registers (gray blocks in Figure 6(a)). Once the first of the triple matricial product is completed, the data transfer to the second array begins. The control unit block guarantees the correct synchronization between the arrival of the input data and the computations for each PE. The result buffer of Figure 6(b) consists of a shift buffer used to store the  elements generated in parallel by the boundary PEs. Finally, the bus interface unit realizes the communication between the systolic array and the embedded processor.
elements generated in parallel by the boundary PEs. Finally, the bus interface unit realizes the communication between the systolic array and the embedded processor.
The second systolic array (referred to as the PSM coprocessor) implements the computation of the Point Spread Matrix (PSM) function  concurrently over the azimuth and range axes, that is
concurrently over the azimuth and range axes, that is  , where, as previously, symbol
, where, as previously, symbol  specifies the concurrent execution of the corresponding computational operations. In the PSM function, both matrices
specifies the concurrent execution of the corresponding computational operations. In the PSM function, both matrices  and
and  are band-Toeplitz type matrices (dim
are band-Toeplitz type matrices (dim
 ; dim
; dim
 ) with the widths of the non-zero strips equal to
) with the widths of the non-zero strips equal to  and
and  , correspondingly, where due to the PSM sparseness,
, correspondingly, where due to the PSM sparseness,  and
and  . Thus, to perform the required reconstruction over the azimuth direction, it is possible to achieve full parallelism with only an
. Thus, to perform the required reconstruction over the azimuth direction, it is possible to achieve full parallelism with only an  rectangular array (as opposed to an original full-dimensional
rectangular array (as opposed to an original full-dimensional  array in the general case [10, 21]). Due to the range-azimuth factorization, the same parallelism is achievable in the range direction as well with the corresponding
array in the general case [10, 21]). Due to the range-azimuth factorization, the same parallelism is achievable in the range direction as well with the corresponding  rectangular systolic array. The matrix multiplication of two band-Toeplitz type matrices employs now the following specifications in the transformations defined by (37):
rectangular systolic array. The matrix multiplication of two band-Toeplitz type matrices employs now the following specifications in the transformations defined by (37):  for the vector schedule,
for the vector schedule,  for the projection vector,
for the projection vector,  for the space processor that determine the resulting transformation matrix
for the space processor that determine the resulting transformation matrix  (37). The topological distribution of the processing elements (PEs) in such systolic structure is shown in Figure 7(a). The corresponding PSM systolic coprocessor architecture is presented in Figure 7(b) with three independent directions of data flow.
(37). The topological distribution of the processing elements (PEs) in such systolic structure is shown in Figure 7(a). The corresponding PSM systolic coprocessor architecture is presented in Figure 7(b) with three independent directions of data flow.
The third coprocessor (referred to as the Iterative POCS coprocessor) performs the adaptive updating of the iterative reconstruction operator  in the corresponding fixed-point DEDR-POCS procedure (32). The key operations of this coprocessor are to perform the standard 1-D convolution and the vector-matrix multiplication. The systolic array for performing the 1-D convolution employs now the following specifications in the transformations defined by (37):
in the corresponding fixed-point DEDR-POCS procedure (32). The key operations of this coprocessor are to perform the standard 1-D convolution and the vector-matrix multiplication. The systolic array for performing the 1-D convolution employs now the following specifications in the transformations defined by (37):  for the vector schedule,
for the vector schedule,  for the projection vector, and
for the projection vector, and  for the space processor that determine the resulting transformation matrix
for the space processor that determine the resulting transformation matrix  (37). Figure 8(a) illustrates the 1-D convolution systolic array and Figure 8(b) presents the relevant systolic architecture.
(37). Figure 8(a) illustrates the 1-D convolution systolic array and Figure 8(b) presents the relevant systolic architecture.
In summary, the developed systolic architectures perform the parallel and pipelined schemes which exploit the proposed above mapping methodology. These architectures provide the necessary HW-level implementation of the SW-optimized complex multi-purpose RS imaging algorithms.
6. Simulations and Performance Analysis
6.1. Simulation Experiment Specifications
In the verification simulation experiments, we considered a conventional single-look SAR with the fractionally synthesized aperture as an RS imaging system [1, 2]. Recall, that signal formation operator (SFO) of such a SAR is factored along two axes in the image plane [3]: the azimuth or cross-range coordinate (horizontal axis, x) and the slant range (vertical axis, y), respectively. We considered the conventional triangular SAR range ambiguity function (AF) [3]  (y) and Gaussian approximation [5, 6],
(y) and Gaussian approximation [5, 6],  of the SAR azimuth AF with the adjustable fractional parameter, a. Note that in the imaging radar applications [3, 4], an AF is referred to as the continuous-form approximation of the PSM
of the SAR azimuth AF with the adjustable fractional parameter, a. Note that in the imaging radar applications [3, 4], an AF is referred to as the continuous-form approximation of the PSM  defined by (25) and serves as an equivalent to the point spread function in the conventional image processing terminology [9]. The image degradation and noising effects were incorporated to simulate the process of formation of the degraded speckle-corrupted MSF images. First, following [1, 3] the degradation in the spatial resolution due to the fractional aperture synthesis mode were simulated via blurring the original image with the range AF
defined by (25) and serves as an equivalent to the point spread function in the conventional image processing terminology [9]. The image degradation and noising effects were incorporated to simulate the process of formation of the degraded speckle-corrupted MSF images. First, following [1, 3] the degradation in the spatial resolution due to the fractional aperture synthesis mode were simulated via blurring the original image with the range AF  along the y axis and with the azimuth AF
along the y axis and with the azimuth AF  along the x axis, respectively. Next, the degradations at the image-formation level due to the propagation and calibration uncertainties were simulated using the statistical model of a SAR image defocusing [2, 3]. For a considered single-look SAR, the conventional MSF image formation algorithm (30) implies, first, application of the regular adjoint SFO
along the x axis, respectively. Next, the degradations at the image-formation level due to the propagation and calibration uncertainties were simulated using the statistical model of a SAR image defocusing [2, 3]. For a considered single-look SAR, the conventional MSF image formation algorithm (30) implies, first, application of the regular adjoint SFO  to the zero-mean Gaussian data realization u, and second, performing the element-by-element (i.e., pixel-by-pixel) squared detection of S+u to compose the corresponding SSP pixel estimates
to the zero-mean Gaussian data realization u, and second, performing the element-by-element (i.e., pixel-by-pixel) squared detection of S+u to compose the corresponding SSP pixel estimates  . Consequently, the MSF pixel estimates
. Consequently, the MSF pixel estimates  are chi-squared distributed
are chi-squared distributed  with two degrees of freedom, and such a distribution is a negative exponential Rayleigh distribution [2, 9]. Thus, to comply with the technically-motivated MSF image formation scheme, the composite multiplicative noise was simulated as a realization of the
with two degrees of freedom, and such a distribution is a negative exponential Rayleigh distribution [2, 9]. Thus, to comply with the technically-motivated MSF image formation scheme, the composite multiplicative noise was simulated as a realization of the  -distributed random variables with the pixel mean value assigned to the actual degraded scene image pixel that directly obeys the statistical speckle model [2, 5, 6]. Such signal-dependent multiplicative image noise dominates the additive noise component in the data in the sense that
-distributed random variables with the pixel mean value assigned to the actual degraded scene image pixel that directly obeys the statistical speckle model [2, 5, 6]. Such signal-dependent multiplicative image noise dominates the additive noise component in the data in the sense that  , hence the estimate
, hence the estimate  performed empirically via the application of the local statistics method [2] was used to adjust the regularization degrees of freedom (regularization factors) in all simulated DEDR-related SSP reconstruction procedures.
performed empirically via the application of the local statistics method [2] was used to adjust the regularization degrees of freedom (regularization factors) in all simulated DEDR-related SSP reconstruction procedures.
We have run the simulation experiments for both certain and uncertain operational scenarios. In the both scenarios, we considered the MSF, RSF and RASF algorithms from the DEDR-POCS family (22). Also, to compare the developed algorithms with the conventional SAR image enhancement techniques [1–3], the celebrated Lee adaptive de-speckling filter based on the local statistics method [2] was simulated. The family of four simulated techniques were renumbered as  . The first one (p
. The first one (p 1) relates to the conventional MSF estimator (30) that employs the adjoint SO
1) relates to the conventional MSF estimator (30) that employs the adjoint SO 

 . This degraded MSF image
. This degraded MSF image  {
{ } was then post-processed applying the Lee adaptive de-speckling filter [2] that we refer to as the adaptively de-speckled MSF image
} was then post-processed applying the Lee adaptive de-speckling filter [2] that we refer to as the adaptively de-speckled MSF image  , that is, p
, that is, p 2. Next, the non-adaptive RSF algorithm with the solution operator
2. Next, the non-adaptive RSF algorithm with the solution operator 

 defined by (19) was applied to enhance the original MSF image
defined by (19) was applied to enhance the original MSF image  employing the iterative DEDR-RSF version of the unified fixed-point iterative procedure (32); the resulting DEDR-RSF enhanced image was specified as
employing the iterative DEDR-RSF version of the unified fixed-point iterative procedure (32); the resulting DEDR-RSF enhanced image was specified as  L
L and numbered as p
and numbered as p 3. Last, the fourth simulated technique corresponds to the adaptive DEDR-RASF method (32) with the optimal solution operator
3. Last, the fourth simulated technique corresponds to the adaptive DEDR-RASF method (32) with the optimal solution operator 
 given by (21); the resulting adaptively enhanced DEDR-RASF image was specified as
given by (21); the resulting adaptively enhanced DEDR-RASF image was specified as  L
L and numbered correspondingly as
and numbered correspondingly as  . In the second (uncertain) simulated scenario, the system AF was additionally distorted over the azimuth frame within the realistic interval of
. In the second (uncertain) simulated scenario, the system AF was additionally distorted over the azimuth frame within the realistic interval of  that corresponds to the partially uncompensated carrier trajectory deviations interval [2, 10]. For both scenarios, the simulations were run for different composite signal-to-noise ratios (SNR) μ defined as the ratio of the average signal component in the rough image formed using the MSF algorithm (30) to the relevant noise component in the same image,
that corresponds to the partially uncompensated carrier trajectory deviations interval [2, 10]. For both scenarios, the simulations were run for different composite signal-to-noise ratios (SNR) μ defined as the ratio of the average signal component in the rough image formed using the MSF algorithm (30) to the relevant noise component in the same image, where
where  represents the average gray level of the original scene image.
represents the average gray level of the original scene image.
6.2. Performance Metrics
The first adopted quality metric was borrowed from the classical image reconstruction applications [9] defined as an improvement in the output signal-to-noise ratio (IOSNR):

where  represents the value of the k th element (pixel) of the original image
represents the value of the k th element (pixel) of the original image  ,
,  represents the value of the k th element (pixel) of the degraded image formed applying the MSF technique (37), and
represents the value of the k th element (pixel) of the degraded image formed applying the MSF technique (37), and  represents a value of the k th pixel of the image reconstructed with three simulated enhancement methods,
represents a value of the k th pixel of the image reconstructed with three simulated enhancement methods,  where
where  corresponds to the adaptive de-speckling algorithm based on the local statistics method [2],
corresponds to the adaptive de-speckling algorithm based on the local statistics method [2],  corresponds to the POCS-RSF algorithm and
corresponds to the POCS-RSF algorithm and  corresponds to the POCS-RASF algorithm, that is, the best one from the developed DEDR-POCS family, respectively. The second adopted metric, the so-called mean absolute error (MAE), was employed as a metric suitable for quantification of edges and fine detail preservation in the reconstructed image defined as [15]
corresponds to the POCS-RASF algorithm, that is, the best one from the developed DEDR-POCS family, respectively. The second adopted metric, the so-called mean absolute error (MAE), was employed as a metric suitable for quantification of edges and fine detail preservation in the reconstructed image defined as [15]

According to these quality metrics, the higher is the IOSNR, and the lower is the MAE, the better is the improvement of the image enhanced/reconstructed with the particular employed algorithm.
6.3. Simulations
In this study, the simulations were performed with a large scale (1K-by-1K) pixel-format image borrowed from the real-world high-resolution terrain SAR imagery (south-west Guadalajara region, Mexico [24]). The quantitative measures of the image enhancement/reconstruction performance gains achieved with the particular employed POCS-RSF and POCS-RASF techniques for different SNRs evaluated with two different quality metrics (38), (39) are reported in Table 2. Figure 9 shows the original scene image (not observable with the simulated SAR systems). Figure 10 illustrates the same original test scene represented in MATLAB pseudocolor scale.
 2, 3, 4 (2) adaptive despeckling filter; (3) DEDR-RSF; (4) DEDR-RASF; results are reported for the certain and uncertain simulated scenarios.
2, 3, 4 (2) adaptive despeckling filter; (3) DEDR-RSF; (4) DEDR-RASF; results are reported for the certain and uncertain simulated scenarios.The images of Figures 11(a) through 11(h) present the results of image formation and enhancement applying different DEDR-related estimators without model uncertainties as specified in the figure captions. In the second simulated scenario, the fractional SAR system suffered from more severe degradations because of the additional system defocusing and multiplicative speckle noising due to the operational scenario uncertainties. Figures 12(a) through 12(h) present the results of image formation and enhancement applying different DEDR-related estimators in the simulated uncertain operational scenario as specified in the figure captions. From the analysis of the reported simulation results, it is evident that the RASF method overperformed the robust nonadaptive RSF in both simulated scenarios. This demonstrates that employing the adaptive RASF technique from the DEDR-POCS family one could substantially improve the quality of the RS images (reconstructed from both certain and uncertain RS measurement data) approaching in the same time (near) real-time computational performances.
Simulation results for certain observation scenario: (SNR
 ): (a) degraded scene image formed applying the MSF method; (b) the same degraded scene represented in the MATLAB pseudo-color scale; (c) image reconstructed applying the Lee adaptive de-speckling algorithm; (d) the same adaptively de-speckled scene represented in the MATLAB pseudo-color scale; (e) image reconstructed applying the POCS-RSF algorithm; (f) image reconstructed applying the POCS-RSF algorithm represented in the MATLAB pseudo-color scale; (g) image reconstructed applying the POCS-RASF algorithm; (h) image reconstructed applying the POCS-RASF algorithm represented in the MATLAB pseudo-color scale.
): (a) degraded scene image formed applying the MSF method; (b) the same degraded scene represented in the MATLAB pseudo-color scale; (c) image reconstructed applying the Lee adaptive de-speckling algorithm; (d) the same adaptively de-speckled scene represented in the MATLAB pseudo-color scale; (e) image reconstructed applying the POCS-RSF algorithm; (f) image reconstructed applying the POCS-RSF algorithm represented in the MATLAB pseudo-color scale; (g) image reconstructed applying the POCS-RASF algorithm; (h) image reconstructed applying the POCS-RASF algorithm represented in the MATLAB pseudo-color scale.
Simulation results for uncertain observation scenario: (SNR
 dB): (a) degraded scene image formed applying the MSF method; (b) the same degraded scene represented in the MATLAB pseudo-color scale; (c) image reconstructed applying the Lee adaptive de-speckling algorithm; (d) the same adaptively de-speckled scene represented in the MATLAB pseudo-color scale; (e) image reconstructed applying the POCS-RSF algorithm; (f) image reconstructed applying the POCS-RSF algorithm represented in the MATLAB pseudo-color scale; (g) image reconstructed applying the POCS-RASF algorithm; (h) image reconstructed applying the POCS-RASF algorithm represented in the MATLAB pseudo-color scale.
dB): (a) degraded scene image formed applying the MSF method; (b) the same degraded scene represented in the MATLAB pseudo-color scale; (c) image reconstructed applying the Lee adaptive de-speckling algorithm; (d) the same adaptively de-speckled scene represented in the MATLAB pseudo-color scale; (e) image reconstructed applying the POCS-RSF algorithm; (f) image reconstructed applying the POCS-RSF algorithm represented in the MATLAB pseudo-color scale; (g) image reconstructed applying the POCS-RASF algorithm; (h) image reconstructed applying the POCS-RASF algorithm represented in the MATLAB pseudo-color scale.
Next in Figure 13, we present the convergence curves related to the iterative-form implementation of the POCS-RSF/RASF techniques for the test case SNR (i.e.,
SNR (i.e., ). From the analysis of these curves one can deduce that after 40 iterations both POCS-RSF and POCS-RASF algorithms begin to suffer from some numerical instabilities. This type of numerical instability is a subtle issue in constructing the regularized iterative techniques for different ill-conditioned problems, for example [1, 3, 9], and so forth. Moreover, the relationship between the resulting IOSNR quality metric and the visual reconstructed image quality is not fully understood, although, of course, one would expect a high degree of correlation between the two [9]. These observations are in concord with the similar observations from other studies of the inverse imaging problems in other ill-posed contexts, for example, [1, 2, 9, 10]. In our case, due to the POCS regularization, the appearance of the DEDR reconstructed images demonstrated substantial improvement up to 15 iterations from the MSF starting point. Next, the appearance of the reconstructed images changed very little from that of the 15 to 25 iterations. The changes became perceptually undistinguishable after 25
). From the analysis of these curves one can deduce that after 40 iterations both POCS-RSF and POCS-RASF algorithms begin to suffer from some numerical instabilities. This type of numerical instability is a subtle issue in constructing the regularized iterative techniques for different ill-conditioned problems, for example [1, 3, 9], and so forth. Moreover, the relationship between the resulting IOSNR quality metric and the visual reconstructed image quality is not fully understood, although, of course, one would expect a high degree of correlation between the two [9]. These observations are in concord with the similar observations from other studies of the inverse imaging problems in other ill-posed contexts, for example, [1, 2, 9, 10]. In our case, due to the POCS regularization, the appearance of the DEDR reconstructed images demonstrated substantial improvement up to 15 iterations from the MSF starting point. Next, the appearance of the reconstructed images changed very little from that of the 15 to 25 iterations. The changes became perceptually undistinguishable after 25 30 iterations. This behavior can be used as a motivation for the empirical stopping rule at 25
30 iterations. This behavior can be used as a motivation for the empirical stopping rule at 25 30 iterations of the POCS-regularized iterative POCS-RSF and POCS-RASF algorithms.
30 iterations of the POCS-regularized iterative POCS-RSF and POCS-RASF algorithms.
6.4. HW/SW Codesign Performance Analysis
In this section, we complete our study with the comparative analysis of the computational complexities of the simulated iterative DEDR-POCS algorithms implemented using the systolic coprocessors constructed following the addressed HW/SW codesign approach. The synthesis metrics related to the implementation of the systolic arrays architectures as coprocessors are summarized in Table 3. First, we exemplify the MSF, PSM and iterative POCS coprocessor architectures for the following simplified specifications: data matrices of size  and two Band-Toeplitz PSF matrices of the same
and two Band-Toeplitz PSF matrices of the same  pixel size with equal bandwidths of 2
pixel size with equal bandwidths of 2 and 2
and 2 pixels. The relevant SP performance analysis results are resumed in Table 3. Next, in Figures 14(a) through 14(c), we summarize the relevant HW synthesis performances for the realistic case of large-scale processed RS scenes (e.g., to
pixels. The relevant SP performance analysis results are resumed in Table 3. Next, in Figures 14(a) through 14(c), we summarize the relevant HW synthesis performances for the realistic case of large-scale processed RS scenes (e.g., to  pixel size) and report the overall resource utilization performances attained with the proposed HW coprocessors architectures for different number of processing elements (PEs).
pixel size) and report the overall resource utilization performances attained with the proposed HW coprocessors architectures for different number of processing elements (PEs).
 and two Band-Toeplitz PSF matrices of the same
and two Band-Toeplitz PSF matrices of the same  pixel size with equal bandwidths of 2
pixel size with equal bandwidths of 2
 3 and 2
3 and 2
 3.
3.Next, the reported metrics of Table 3 specify the area and time behaviors of the corresponding hardware systolic arrays, that is the corresponding MSF, the PSM, and the iterative POCS architectures specified above in Section 5. From the analysis of the data reported in Table 3 and Figures 14(a) through 14s(c), one can deduce the following: With the proposed HW/SW codesign architecture (in which the embedded processors iterate properly the corresponding SP procedures) the DEDR-POCS-related algorithms can be efficiently implemented in an iterative fixed-point fashion also for the realistic large-scale scenes (e.g.,  pixel size). Pursuing the proposed systolic computing architecture concept, the increased scene dimensionality requires the proper segmentation of the scene frame with the parallelized computing performed over the partitioned segments followed by the relevant integration of the overall partial processed data. Such partitioned systolic HW/SW codesign computing-oriented processing can be performed directly following the architecture design concept proposed and specified in the previous Section 5.4. Additionally, the scalability in terms of Flip-Flops, Slices and LUTs (i.e., the HW resources of the FPGA) for the proposed MSF, PSM and iterative POCS coprocessors are reported in Figures 14(a) through 14(c). In fact, the corresponding DEDR-related SP algorithms can be efficiently implemented in a Field Programmable Systems on Chip (FPSoC) mode in spite of employing conventional systems based on multi-FPGAs or PC-Clusters [12–14, 16]. The latter is practically inspired and desirable for a wide range of RS and general SP applications due to the large range density of the existing FPGAs that incorporate huge resources of logical gates, block RAM memory modules and soft or hard-embedded processors integrated on the same chip with the relevant custom co-processing HW blocks, and so forth. For example, an alternative approach for high-speed computational implementation of the reconstructive RS image processing based on the use of clusters of PCs was presented in [12–14]. In [12], the cluster NSPO Parallel TestBed for performing parallel radiometric and geometrical corrections of the large-scale 3600
pixel size). Pursuing the proposed systolic computing architecture concept, the increased scene dimensionality requires the proper segmentation of the scene frame with the parallelized computing performed over the partitioned segments followed by the relevant integration of the overall partial processed data. Such partitioned systolic HW/SW codesign computing-oriented processing can be performed directly following the architecture design concept proposed and specified in the previous Section 5.4. Additionally, the scalability in terms of Flip-Flops, Slices and LUTs (i.e., the HW resources of the FPGA) for the proposed MSF, PSM and iterative POCS coprocessors are reported in Figures 14(a) through 14(c). In fact, the corresponding DEDR-related SP algorithms can be efficiently implemented in a Field Programmable Systems on Chip (FPSoC) mode in spite of employing conventional systems based on multi-FPGAs or PC-Clusters [12–14, 16]. The latter is practically inspired and desirable for a wide range of RS and general SP applications due to the large range density of the existing FPGAs that incorporate huge resources of logical gates, block RAM memory modules and soft or hard-embedded processors integrated on the same chip with the relevant custom co-processing HW blocks, and so forth. For example, an alternative approach for high-speed computational implementation of the reconstructive RS image processing based on the use of clusters of PCs was presented in [12–14]. In [12], the cluster NSPO Parallel TestBed for performing parallel radiometric and geometrical corrections of the large-scale 3600 2944-pixel RS images was implemented. The reconstructive image processing was conducted using a PC-Cluster composed by three PCs each one with a Pentium-III 550 MHz with 128 MB of RAM connected with 100 Mbps Fast-Ethernet LAN. The processing time achieved with such three-PCs cluster was only 33.3 seconds (near-real time for conventional RS users), while the corresponding processing performed with one single processor required 84.65 seconds. In [13, 14], another kind of parallel architecture was implemented for morphological classification of hyperspectral RS imagery at the NASA's Goddard Space Flight Center. The parallel classifier of [14] uses 256-processor Beowulf cluster (Thunderhead cluster) with hybrid neural parallelism that enables such a system to perform an accurate classification of the hyperspectral RS scenes in only 17 seconds.
2944-pixel RS images was implemented. The reconstructive image processing was conducted using a PC-Cluster composed by three PCs each one with a Pentium-III 550 MHz with 128 MB of RAM connected with 100 Mbps Fast-Ethernet LAN. The processing time achieved with such three-PCs cluster was only 33.3 seconds (near-real time for conventional RS users), while the corresponding processing performed with one single processor required 84.65 seconds. In [13, 14], another kind of parallel architecture was implemented for morphological classification of hyperspectral RS imagery at the NASA's Goddard Space Flight Center. The parallel classifier of [14] uses 256-processor Beowulf cluster (Thunderhead cluster) with hybrid neural parallelism that enables such a system to perform an accurate classification of the hyperspectral RS scenes in only 17 seconds.
As a result, advances on high performance computing as well as on specialized high performance hardware modules are necessarily required to achieve the near-real processing time performances for complex RS algorithms.
Last, we compared the required processing time of the general-form RSF/RASF DEDR-related procedures (22) and the iterative fixed-point DEDR-POCS-regularized algorithm (32), both implemented using the conventional MATLAB software in a personal computer (PC) running at 3 GHz with a AMD Athlon (tm) 64 dual-core processor and 2 GB of RAM memory. Also, the same DEDR-related algorithms were implemented using the proposed HW/SW codesign architecture (soft- and hardware) without systolic and with systolic arrays employing the Xilinx FPGA XC4VSX35-10ff668. The corresponding comparative results are reported in Table 4. Analyzing these reported results, one may deduce the following. The iterative fixed-point DEDR-POCS-regularized algorithm (32) manifests the (near) real time high-resolution enhancement/reconstruction of the RS imagery. The implementation of the proposed HW/SW codesign architecture helps to reduce drastically the overall processing time. Particularly, the proposed implementation of the iterative POCS-regularized RASF algorithm with systolic arrays takes only 2.56 seconds for each iteration of the image reconstruction. In total, it takes 64 sec for 25 iterations. This new computation time is approximately 3 times less than the previous implementation without systolic arrays [10], 8 times less than the corresponding processing time achievable with the MATLAB POCS-based implementation, and it is  times less than the hypothetical processing time required for implementing the full-format conventional general-form DEDR-RASF algorithm (22) without POCS regularization and without systolic computing.
times less than the hypothetical processing time required for implementing the full-format conventional general-form DEDR-RASF algorithm (22) without POCS regularization and without systolic computing.
7. Concluding Remarks
The principal result of the undertaken study relates to the digital signal processing-oriented solution of the RS image enhancement/reconstruction problems in a (near) real time computing mode (the "near real time" being understood in context of conventional RS users) via exploiting the aggregated hardware/software (HW/SW) codesign paradigm that results in an efficient hardware implementation architecture based on the use of systolic array processors. We have approached the goal of the (near) real time computational implementation of the enhancement/reconstruction of the RS imagery from two directions. First, we have analytically established that to alleviate the problem ill-posedness and reduce the overall computational load of the large-scale image enhancement/reconstruction tasks at the algorithmic processing level, some special form of descriptive experiment design projection-type numerical regularization must be employed. This stage was developed and addressed here as the unified DEDR method, and the efficient fixed-point numerical iterative technique that incorporates the proper construction of the relevant orthogonally factorized regularizing projector onto convex sets (POCS) in the solution domain was designed and specified for the particular employed RS sensor system, namely, the side-looking imaging synthetic aperture radar (SAR) operating in both certain and uncertain scenarios. We have also examined how such SAR-adapted POCS-regularized fixed-point iterative technique can be executed concurrently over the orthogonal range-azimuth coordinates with optimal use of the sparseness properties of the overall SAR system point spread function characteristics. The algorithmic-level advantages of such unified DEDR-POCS-regularized RS image enhancement/reconstruction techniques relate to the theoretically guaranteed convergence of the corresponding fixed-point iterative process with the proper factorization of the numerical reconstructive procedures over the orthogonal range-azimuth directions in the representation image frame.
Second, we have examined that pursuing the proposed HW/SW codesign paradigm and employing the systolic arrays as co-processing units, the (near) real time image processing requirements can be achieved due to performing the corresponding computations in an efficient systolic architecture mode. The unified algorithmic (software-level, SW) and systematic (hardware-level, HW) codesign approach was verified via computer simulation experiments indicative of its efficiency for performing the RS image enhancement and reconstruction tasks in (near) real computational time. The tested DEDR-POCS-related techniques implemented numerically using the proposed HW/SW codesigned computational architecture overperform the previously developed methods both in the attained reconstruction quality and the achievable computational complexity, that is manifest the substantially reduced overall computational time (e.g., up to three orders with respect to the schemes that do not aggregate the POCS regularization with the systolic computing). We do believe that pursuing the DEDR-POCS-related HW/SW codesign paradigm with systolic array hardware accelerators one could approach definitely the real time computational requirements while performing the reconstructive processing of the large-scale RS imagery attaining the enhancement/reconstruction performance gains close to the limiting bounds.
References
Wehner DR: High-Resolution Radar. 2nd edition. Artech House, Boston, Mass, USA; 1994.
Lee JS: Speckle suppression and analysis for synthetic aperture radar images. Optical Engineering 1986, 25(5):636-643.
Henderson FM, Lewis AV: Principles and applications of imaging radar. In Manual of Remote Sensing. 3rd edition. John Wiley & Sons, New York, NY, USA; 1998.
Shkvarko YV: Estimation of wavefield power distribution in the remotely sensed environment: Bayesian maximum entropy approach. IEEE Transactions on Signal Processing 2002, 50(9):2333-2346. 10.1109/TSP.2002.801916
Shkvarko YV: Unifying regularization and Bayesian estimation methods for enhanced imaging with remotely sensed data—part I: theory. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(5):923-931.
Shkvarko YV: Unifying regularization and Bayesian estimation methods for enhanced imaging with remotely sensed data—part II: implementation and performance issues. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(5):932-940.
Shkvarko YV: From matched spatial filtering towards the fused statistical descriptive regularization method for enhanced radar imaging. EURASIP Journal on Applied Signal Processing 2006, 2006:-9.
Shkvarko YV, Perez-Meana H, Castillo-Atoche A: Enhanced radar imaging in uncertain environment: a descriptive experiment design regularization paradigm. International Journal of Navigation and Observation 2008, 2008:-11.
Barrett HH, Myers KJ: Foundations of Image Science. John Willey & Sons, New York, NY, USA; 2004.
Castillo A, Shkvarko YV, Torres D, Perez HM: Convex regularization-based hardware/software co-design for real-time enhancement of remote sensing imagery. International Journal of Real Time Image Processing 2008, 4(3):261-272.
Ponomaryov VI: Real-time 2D-3D filtering using order statistics based algorithms. Journal of Real-Time Image Processing 2007, 1(3):173-194. 10.1007/s11554-007-0021-5
Yang CT, Chang CL, Hung CC, Wu F: Using a Beowulf cluster for a remote sensing application. Proceedings of the 22nd Asian Conference on Remote Sensing, November 2001, Singapore 1:
Thunderhead System http://newton.gsfc.nasa.gov/thunderhead/
Plaza A, Plaza J: Parallel morphological classification of hyperspectral imagery using extended opening and closing by reconstruction operations. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '08), July 2008, Boston, Mass, USA I.58-I.61.
Meyer-Baese U: Digital Signal Processing with Field Programmable Gate Array. Springer, Berlin, Germany; 2001.
Greco J, Cieslewski G, Jacobs A, Troxel IA, George AD: Hardware/software interface for high-performance space computing with FPGA coprocessors. Proceedings of the IEEE Aerospace Conference, March 2006, Big Sky, Mont, USA 10-25.
Fixed-Point Toolbo
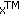 User's Guide, MATLAB http://www.mathworks.com/
User's Guide, MATLAB http://www.mathworks.com/EDK 9.1 MicroBlaze tutorial in Virtex-4 Xilinx, http://www.xilinx.com/
Marquardt A, Betz V, Rose J: Speed and area tradeoffs in cluster-based FPGA architectures. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2000, 8(1):84-93.
López-Vallejo M, López JC: On the hardware-software partitioning problem: system modeling and partitioning techniques. ACM Transactions on Design Automation of Electronic Systems 2003, 8(3):269-297. 10.1145/785411.785412
Lo SC, Jean SN: Mapping algorithms to VLSI array processors. Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP '88), 1988, New York, NY, USA 2033-2036.
Kung SY: VLSI Array Processors. Prentice Hall, Upper Saddle River, NJ, USA; 1988.
Xilinx Application Note XAPP967: creating an OPB IPIF-based IP and using it in EDK 2007.
Space Imaging GeoEye, 2008, http://www.euspaceimaging.com/
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Castillo Atoche, A., Torres Roman, D. & Shkvarko, Y. Experiment Design Regularization-Based Hardware/Software Codesign for Real-Time Enhanced Imaging in Uncertain Remote Sensing Environment. EURASIP J. Adv. Signal Process. 2010, 254040 (2010). https://doi.org/10.1155/2010/254040
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/254040
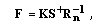
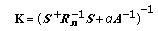
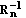 is the noise whitening filter, and the adjoint (i.e., Hermitian transpose) SFO
is the noise whitening filter, and the adjoint (i.e., Hermitian transpose) SFO  defines the matched spatial filter in the conventional signal processing terminology [
defines the matched spatial filter in the conventional signal processing terminology [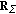 that yields [
that yields [
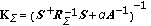
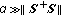 , that is, the case of a dominating priority of suppression of noise over the systematic error in the optimization problem (6). In this case, the SO (14) is approximated by the matched spatial filter (MSF) [
, that is, the case of a dominating priority of suppression of noise over the systematic error in the optimization problem (6). In this case, the SO (14) is approximated by the matched spatial filter (MSF) [
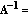 I) and balanced minimization of the systematic and noise error measures in (9), (11) by adjusting the regularization parameter
I) and balanced minimization of the systematic and noise error measures in (9), (11) by adjusting the regularization parameter  to the inverse of the signal-to-noise ratio (SNR). In that case the SO becomes the Tikhonov-type robust spatial filter (RSF) [
to the inverse of the signal-to-noise ratio (SNR). In that case the SO becomes the Tikhonov-type robust spatial filter (RSF) [
 RSF
is adjusted to a particular operational scenario model, namely,
RSF
is adjusted to a particular operational scenario model, namely, 
 (
( /
/ ) for the case of a certain operational scenario [
) for the case of a certain operational scenario [
 (
( /
/ ) in the uncertain operational scenario case [
) in the uncertain operational scenario case [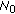 represents the white observation noise power density,
represents the white observation noise power density, 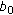 is the average a priori SSP value, and
is the average a priori SSP value, and 

 +
+ 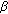 corresponds to the augmented noise power density in the correlation matrix specified by (13).
corresponds to the augmented noise power density in the correlation matrix specified by (13). and A are adjusted in an adaptive fashion following the Bayesian minimum risk strategy [
and A are adjusted in an adaptive fashion following the Bayesian minimum risk strategy [
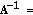
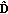
 diag(
diag( ), the diagonal matrix with the estimate
), the diagonal matrix with the estimate  at its principal diagonal, in which case the SOs (14), (16) become itself solution-dependent operators that result in the following robust adaptive spatial filters (RASFs):
at its principal diagonal, in which case the SOs (14), (16) become itself solution-dependent operators that result in the following robust adaptive spatial filters (RASFs):

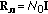 , attributing the unknown correlated noise component as well as multiplicative speckle noise to the composite uncertain noise term
, attributing the unknown correlated noise component as well as multiplicative speckle noise to the composite uncertain noise term 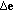 in (2), in which case
in (2), in which case 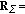
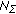 I with the composite noise power density
I with the composite noise power density 


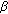 , the initial observation noise variance
, the initial observation noise variance 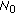 augmented by the loading factor
augmented by the loading factor 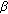 specified by (13).
specified by (13).


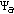 and
and  factorized over the azimuth and range axes can be calculated concurrently that we refer to as
factorized over the azimuth and range axes can be calculated concurrently that we refer to as 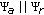 , where symbol
, where symbol  specifies now the concurrent execution of the corresponding computational operations.
specifies now the concurrent execution of the corresponding computational operations.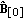 can be computed using the same factorized structure analogues to
can be computed using the same factorized structure analogues to 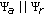 .
. , at the current (i
, at the current (i 1)st iteration step is an iteratively updated function of
1)st iteration step is an iteratively updated function of 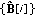 computed at the previous i th iteration that also admits the factorized computing.
computed at the previous i th iteration that also admits the factorized computing.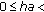 max ha,
max ha, 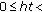 max ht, for each i th hardware coprocessor
max ht, for each i th hardware coprocessor  and
and  max St, for the embedded processor
max St, for the embedded processor  . These three hardware coprocessors
. These three hardware coprocessors  and the embedded processor compose the target architecture
and the embedded processor compose the target architecture  , for the pre-selected FPGA
, for the pre-selected FPGA  with the corresponding pre-determined architecture constraints
with the corresponding pre-determined architecture constraints 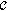 :
: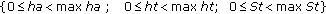 [
[ must satisfy the predefined execution time performance requirements [
must satisfy the predefined execution time performance requirements [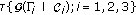 and
and  conditioned by the specified above architecture constraints
conditioned by the specified above architecture constraints 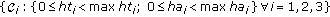 , and
, and 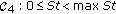 , correspondingly.
, correspondingly.










 User's Guide, MATLAB
User's Guide, MATLAB