- Research Article
- Open access
- Published:
A Metastate HMM with Application to Gene Structure Identification in Eukaryotes
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 581373 (2010)
Abstract
We introduce a generalized-clique hidden Markov model (HMM) and apply it to gene finding in eukaryotes (C. elegans). We demonstrate a HMM structure identification platform that is novel and robustly-performing in a number of ways. The generalized clique HMM begins by enlarging the primitive hidden states associated with the individual base labels (as exon, intron, or junk) to substrings of primitive hidden states, or footprint states, having a minimal length greater than the footprint state length. The emissions are likewise expanded to higher order in the fundamental joint probability that is the basis of the generalized-clique, or "metastate", HMM. We then consider application to eukaryotic gene finding and show how such a metastate HMM improves the strength of coding/noncoding-transition contributions to gene-structure identification. We will describe situations where the coding/noncoding-transition modeling can effectively recapture the exon and intron heavy tail distribution modeling capability as well as manage the exon-start needle-in-the-haystack problem. In analysis of the C. elegans genome we show that the sensitivity and specificity (SN,SP) results for both the individual-state and full-exon predictions are greatly enhanced over the standard HMM when using the generalized-clique HMM.
1. Introduction
Computational gene finding dates back to the 1980s [1–3]. The most successful gene-finding tool has been the hidden Markov model, both in statistics intrinsic to the genome under study (ab initio gene finding) [1–3] and in statistical analysis extrinsic to the genome (homology or EST matching) [4]. Matching, or alignment, of query sequences to a known sequence database is typically done using BLAST [5] (which involves an HMM seed alignment, followed by less optimal, but faster, non-HMM seed-alignment extension). BLAST can also be used for gene finding alone, in homology-based programs to identify new genes by sufficiently aligning a query sequence with a known gene or genes [4]. In [6], they combine homology information with intrinsic genomic information (from statistical properties of the genomic sequence data alone). The main drawback of homology-based approaches is that they appear to be very weak at finding new genes, as discussed in [1], and explored in [7]. This is largely because approximately half of the genes in eukaryotic genomes appear to be novel to that genome (such as for C. elegans). This is likely to be true for humans, where we already know that only 50% of the proteins encoded in chromosome 22, for example, are found to be similar to previously known proteins. In [8], the author describes application of the best gene finders known at the time (c.a. 2004) to gene finding in novel genomes. From that study, it is clear that gene prediction is species specific, that is, an ab initio component must operate for any gene finder to succeed at identifying genes and genomic structures novel to that organism [8].
Beginning c.a. 2000 there was a movement towards consolidation of the intrinsic and extrinsic approaches [7, 9], as described in a 2002 review [9] and a 2006 review [10]. Furthermore, in the 2006 review, it was claimed that "improved modeling efforts at the hidden Markov model level are of relatively little value." We describe here a radical improvement in HMM capabilities in gene finding and likely a number of other areas of application, by introducing a fundamental new development at the model level. Also beginning c.a. 2000 was specialization to sensor development [11–17] to help supplement the HMM-based structure discovery process. There were sensors for transcription start site prediction [6], transcription initiation sites and polyadenylation signals [18], splice-site recognition [19, 20], and identification of 3′ ends of exons by EST analysis [21], to list just a few examples.
The past decade, since 2000, has also seen rapid growth in motif-discovery algorithms—in parallel with the aforementioned sensor specialization (and growing more interdependent, as we describe in the Discussion). Many of these motif-discovery algorithms are beginning to tie into the HMM-based structure identification via referencing regions indicated by the HMM. In [22, 23], many important TFBSs, promoters, and other regulatory motifs can be identified by their position relative to the start and stop of coding (and other nonself transitions identified by the HMM's optimal Viterbi-path parsing). In [22], they find that the motif finding effort is greatly enhanced by referencing to nearby gene structure and identifying "peak regions" where motifs can be isolated. Not surprisingly, if separate statistical profiling is performed on the regions just outside (before and after) the transcription region, then gene finding is improved [22, 24]. Motif discovery can be focused onto the cis-regulatory regions in particular, and if linked with the HMM discovery, the motif-discovery and gene-discovery efforts are simultaneously strengthened. One of the clear benefits of having a very strong intrinsic HMM formulation as a foundation is that the later pairing with motif discovery and signal-sensor augmentations then arrives at a unified and powerful intrinsic/extrinsic gene and motif discovery platform. This capability is enhanced further if zone-dependent emissions are employed via larger metastates (see Section 5) or via reference to HMMD improvements as indicated in [24–26]. The HMM formulation with HMMwD augmentation also provides an optimal means for inclusion of extrinsic statistics (side information) into the Viterbi optimization (as described in [24]). The "scaffolding" provided by the HMM parsing (via the Viterbi path derivation) defines regions where zone-dependent statistics and zone-restricted motif discovery can be applied. Many motif-finding methods would benefit from the alignment referencing provided by the HMM's scaffolding of annotation across coding and noncoding regions. With zone-restricted motif discovery, gap- and hash-interpolated Markov models [27, 28] become powerful tools for motif discovery in a restricted region [18, 28–32]. The approach we describe in this paper, and its companion paper [24], seeks to unify the above approaches within a powerful new HMM-based structure-modeling architecture.
The shortcomings of the HMM due to algorithmic definitions, such as lack of state-duration modeling, are readily apparent (with fixes as described in [24–26]). The shortcomings of the HMM due to model definition and related implementation are more subtle. In an HMM implementation, the number of lookups to a particular emission or transition probability "table" will show how that table's anomalous statistics influence the overall computation (where the count on use of a particular component in the table is precisely what provides an estimation in the HMM Baum-Welch algorithm). Similarly, what is readily observed in implementation of an HMM is the use of various probability tables, and a significant shortcoming is revealed. Standard HMMs lead to a model that strongly de-emphasizes (low table usage) and does not recognize the anomalous statistics known to exist around nonself transitions, and fundamentally, their transition probabilities are not sequence dependent. In this paper, we demonstrate use of transition probabilities that are sequence dependent, via use of a constrained set of "metastates," with comparable computational complexity to the standard HMM. There is, thus, a "choice in model primitives" shortcoming underlying the standard HMM implementations that is resolved in the metastate HMM description to follow.
In this paper, we introduce a generalized-clique, "metastate," hidden Markov model and apply it to the analysis of the genomic structure of C. elegans (a genome-data intrinsic approach, for example, not using EST or homology information). Our metastate HMM generalizes from primitive states to windows of adjacent primitive states (e.g., "footprint states") and does so by only allowing one coding-to-noncoding, or noncoding-to-coding, transition in the window of states. The constraint to have no more than a single "nonself" transition in a footprint is equivalent to a minimum length constraint on exons, introns, and "junk." The linear growth in higher order states with this constraint (proven later) is critical for practical use of the larger footprint size models that will be demonstrated.
The generalized-clique HMM begins by enlarging the primitive hidden states associated with individual base labeling (as exon, intron, or junk) to substrings of primitive hidden states or footprint states—"ieeeeeee," for example, (also a Cajun exclamation). In what follows, the transitions between primitive hidden states for coding  and noncoding
and noncoding  ,
,  are referred to as "eij-transitions," and the self transitions,
are referred to as "eij-transitions," and the self transitions,  , are referred to as "xx-transitions." The emissions are likewise expanded to higher order in the fundamental joint probability that is the basis of the generalized-clique, or "metastate," HMM. We consider application to eukaryotic gene finding and show how a metastate HMM improves the strength of eij-transition contributions to gene-structure identification. We will describe situations where the metastate eij-transition modeling can effectively "recapture" the exon and intron heavy tail distribution modeling capability as well as manage the exon-start "needle-in-the-haystack" problem.
, are referred to as "xx-transitions." The emissions are likewise expanded to higher order in the fundamental joint probability that is the basis of the generalized-clique, or "metastate," HMM. We consider application to eukaryotic gene finding and show how a metastate HMM improves the strength of eij-transition contributions to gene-structure identification. We will describe situations where the metastate eij-transition modeling can effectively "recapture" the exon and intron heavy tail distribution modeling capability as well as manage the exon-start "needle-in-the-haystack" problem.
2. Background
2.1. Genomic Data—with C. elegans Specifics
Once it is fully annotated, genomic data can be unambiguously represented by strings formed from the 4 letters a, c, g, and t denoting the DNA nucleotide bases: adenine, cytosine, guanine, and thymine, respectively. Genes are sequences of DNA nucleotides that encode specific sequences of amino acids to form proteins (with 5′ to 3′ read convention). The data annotation designates the coding and noncoding segments in the genomic data. In eukaryotes, genes consist of coding segments or exons which are delimited internally by special, intragenic, noncoding segments or introns. The inter genic, noncoding regions of bases outside the genes are referred to here as "junk."
The process of removing the intermediate introns and reconnecting (possibly variable subsets of) the resulting exons end-to-end is referred to as splicing. Perhaps the most important role of introns is to provide a mechanism for the formation of alternative combinations and/or subsets of the exons contained in a given gene in order to form alternative proteins also used by the organism in question. These alternative combinations are referred to as alternative splicings.
The C. elegans genome consists of six chromosomes  , containing approx. 97,000,000 base-pairs of DNA. The 90% base accuracy of our metastate HMM is sufficient to isolate and resolve outrons and other structures [33], such as the following dozen attributes.
, containing approx. 97,000,000 base-pairs of DNA. The 90% base accuracy of our metastate HMM is sufficient to isolate and resolve outrons and other structures [33], such as the following dozen attributes.
-
(1)
Approximately 19,000 genes, so approximately 1 gene per 5,000 bases.
-
(2)
Each gene has an average of 5 introns.
-
(3)
Tandem repeats account for 2.7% of genome, inverted repeats 3.6%. Repeats have different families on different chromosomes and are more likely on introns. Common TTAGGC hexamer repeat.
-
(4)
38 dispersed repeat families can potentially be identified via hash-interpolated Markov model [27].
-
(5)
Approximately 50% of genome novel.
-
(6)
Approximately 80% of genes are transspliced to a common spliced leader.
-
(7)
Approximately 20% of genes organized as operons.
-
(8)
Common occurrence of "outron" structure: introns-like sequence with no internal 5' consensus that is found before the first exon.
-
(9)
Genes with trans-splices are often distinguished from those that are not by the presence of an outron.
-
(10)
3' ends of genes within operons typically signaled by AATAA.
-
(11)
Typical translation Initiation: [(A/G)CCATG].
-
(12)
Termination (TAA (61%); TAG (17%); TGA (22%)).
2.2. The Standard 1st Order HMM
We define the 1st order HMM as consisting of the following:
-
(i)
an observable alphabet,
 ,
, -
(ii)
a hidden state alphabet,
 ,
, -
(iii)
"prior" Probabilities
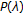 for all
for all 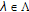 ,
, -
(iv)
"transition" Probabilities
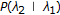 for all
for all 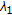
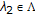 —where the standard transition probability is denoted
—where the standard transition probability is denoted 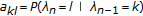 , a 1st order Markov model on states with homogenous stationary statistics (i.e., no dependence on position "
, a 1st order Markov model on states with homogenous stationary statistics (i.e., no dependence on position " "),
"), -
(v)
"emission" Probabilities
 for all
for all 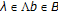 —where the standard emission probability is
—where the standard emission probability is 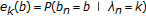 , a 0th order Markov model on bases and with homogenous stationary statistics.
, a 0th order Markov model on bases and with homogenous stationary statistics.
Given the above, there are three classes of problems in which the HMM can be used to solve [34, 35]:
-
(1)
evaluation: determine the probability of occurrence of the observed sequence;
-
(2)
learning: determine the most likely emissions and transition;
-
(3)
decoding (Viterbi): determine the most probable sequence of states emitting the observed sequence.
Here, we focus only on the 3rd problem, the Viterbi decoding problem. The probability of a sequence of observables  being emitted by the sequence of hidden states
being emitted by the sequence of hidden states  is solved by using
is solved by using  in the standard factorization, where the two terms in the factorization are described as the observation model and the state model, respectively. In the 1st order HMM, the state model has the 1st order Markov property, and the observation model is such that the current observation,
in the standard factorization, where the two terms in the factorization are described as the observation model and the state model, respectively. In the 1st order HMM, the state model has the 1st order Markov property, and the observation model is such that the current observation,  , depends only on the current state,
, depends only on the current state,  ,
,

With first-order Markov assumption in the state model, this becomes

In the Viterbi algorithm, a recursive variable is defined (following the notation in [34]) as follows:  = "the most probable path ending in state "k" with observation "
= "the most probable path ending in state "k" with observation " "". The recursive definition of
"". The recursive definition of  is then
is then  , from which the optimal path information is recovered according to the (recursive) traceback
, from which the optimal path information is recovered according to the (recursive) traceback

 , where
, where  , for length
, for length  sequence.
sequence.
2.3. HMM States for Gene-Structure Identification
Exons have a 3-base encoding as directly revealed in a mutual information analysis of gapped base statistical linkages as shown in [27]. The 3-base encoding elements are called codons, and the partitioning of the exons into 3-base subsequences is known as the codon framing. A gene's coding length must be a multiple of 3 bases. The term frame position is used to denote one of the 3 possible positions—0, 1, or 2 by our convention—relative to the start of a codon. Introns may interrupt genes after any frame position. In other words, introns can split the codon framing either at a codon boundary or one of the internal codon positions.
Although there is no notion of framing among introns, for convenience we associate framing with the intron, as indicated in the example below, as a tracking device in order to ensure that the frame of the following introns-to-exon transition is constrained appropriately. The primitive states of the individual bases occurring in exons, introns, and junk are denoted by
Exon states = {e 0 ,e 1 ,e 2 },
Intron states = {i 0 ,i i ,i 2 },
Junk state = {j}.
We have three possible intron framings indicated in the following state strings:
(intron frame 0)
jj ⋯ je 0 e 1 e 2⋯ e 0i 0 i 0 ⋯ i 0 e 1⋯ e 0 e 1 e 2 jj ⋯ j
(intron frame 1)
jj ⋯ je 0 e 1 e 2⋯ e 1i 1 i 1 ⋯ i 1 e 2⋯ e 0 e 1 e 2 jj ⋯ j
(intron frame 2)
jj ⋯ je 0 e 1 e 2⋯ e 2i 2 i 2 ⋯ i 2 e 0⋯ e 0 e 1 e 2 jj ⋯ j
There are 15 unique two-label (dimer) transitions: {jj, je 0 , e 0 e 1 , e 1 e 2 , e 2 e 0 , e 0i 0 , e 1i 1 , e 2i 2 , i 0 i 0 , i 1 i 1 , i 2 i 2 , i 0 e 1 , i 1 e 2 , i 2 e 0 , e 2 j}. In what follows, we split the stop codon into the three possibilities strictly observed {e 2 j_TAA,e 2 j_TAG,e 2 j_TGA}, for a total of 17 states in our forward encoding model.
Encodings for proteins can be found in both directions along the DNA strand. The encodings are sparse, rarely overlapping, and have approximately equal numbers of forward and reverse ("shadow") encodings. The differences in the base statistics in the forward and reverse gene encodings are sufficiently negligible (or disjoint) that their counts can simply be merged in the modeling (data not shown). We incorporate shadow states, indicating reverse encoded exons and introns, into the state model of our metastate HMM, denoted by the primitives by ê and î, respectively. For example, the 3 possible intron framings for the reverse encoding are as follows:
(intron frame 0)
jj ⋯ jê 2 ê 1 ê 0⋯ ê 1 î 0 î 0 ⋯ î 0 ê 0⋯ ê 2 ê 1 ê 0 jj ⋯ j
(intron frame 1)
jj ⋯ jê 2 ê 1 ê 0⋯ ê 2 î 1 î 1 ⋯ î 1 ê 1⋯ ê 2 ê 1 ê 0 jj ⋯ j
(intron frame 2)
jj ⋯ j ê 2 ê 1 ê 0⋯ ê 0 î 2 î 2 ⋯ î 2 ê 2⋯ ê 2 ê 1 ê 0 jj ⋯ j
There are 16 reverse encoding state transitions in direct correspondence with the 16 non-jj state transitions for the forward read. The jj transition couples the forward and reverse reads in that a forward encoding can "end," that is, transition to a region of junk, then eventually transition to a reverse encoded gene. The total number of state transition (dimer states) in our model is, thus, 33.
13 xx-type (homogeneous) dimmers:
-
(a)
6 Intron-intron: i 0 i 0 , i 1 i 1 , i 2 i 2 , î 0 î 0 , î 1 î 1 , î 2 î 2,
-
(b)
6 Exon-exon: e 0 e 1 , e 1 e 2 , e 2 e 0 , ê 0 ê 1 , ê 1 ê 2 , ê 2 ê 0,
-
(c)
1 Junk-junk: jj.
20 eij-type (heterogeneous) dimmers:
-
(d)
6 Exon-intron: e 0 i 0 , e 1 i 1 , e 2 i 2 , ê 0 î 0 , ê 1 î 1 , ê 2 î 2,
-
(e)
6 Intron-exon: i 0 e 1 , i 1 e 2 , i 2 e 0 , î 0 ê 1 , î 1 ê 2 , î 2 ê 0,
-
(f)
6 Exon-junk: (e 2 j)TAA, (e 2 j)TAG, (e 2 j)TGA, (ê 2 j)TAA, (ê 2 j)TAG, (ê 2 j)TGA,
-
(g)
2 Junk-exon: (je 0), (jê 0).
In order to work directly with the above dimer states, or the footprint-state generalization introduced in the Methods, we need to generalize to a higher order HMM model. The standard HMM has emissions that only dependent on the current state (e.g., we have  terms). This leads to poor performance in modeling the anomalous statistics in the transition regions between exon, intron, or junk regions. If a transition "je 0" has occurred, for example, and we are looking at the base emission for the "e 0" state, we cannot account for the prior state with the simple
terms). This leads to poor performance in modeling the anomalous statistics in the transition regions between exon, intron, or junk regions. If a transition "je 0" has occurred, for example, and we are looking at the base emission for the "e 0" state, we cannot account for the prior state with the simple  conditional probabilities in the standard bare-bones HMM modeling, we minimally need
conditional probabilities in the standard bare-bones HMM modeling, we minimally need  , that is, state modeling at the dimer level or higher.
, that is, state modeling at the dimer level or higher.
3. Methods
The Methods section begins with a description of the dataset preparation in Section 1 titled "Selection and Preparation of Datasets…". Section 2, on "Application of Metastate HMM Model to the Test Data," provides an overview of how the datasets and metastate HMM models are used in the testing and tuning. In Section 3, on "The Generalized-Clique HMM Construction," we provide the core new HMM theory that is the underpinning of the new type of HMM modeling enabled. Section 4 gets into the nuts-and-bolts of the "Enumeration of the Footprint States" in the metastate HMM, and Section 5 to follow provides the "Measures of Predictive Performance That Are Used."
3.1. Selection and Preparation of Datasets for Preliminary Testing and "Raw" Genome Analysis
In [16], the authors performed the following steps to arrive at the ALLSEQ dataset [36].
-
(1)
Select the set of all sequences encoding at lease one complete protein from the vertebrate divisions of GenBank Release 85.0 (October 15, 1994) .
-
(2)
From the above discard the following:
-
(a)
any sequence encoding at least one incomplete protein,
-
(b)
any sequence for which the exact coding regions was not unambiguous,
-
(c)
any sequence encoding a protein in the complementary (reverse encoding) strand,
-
(d)
any sequence containing a gene or part of a gene associated with other sequences,
-
(e)
any sequence encoding a pseudogene (via "CDS Key" value "/pseudo") ,
-
(f)
any sequence encoding more than one gene or alternative splicing of a gene,
-
(g)
any sequence encoding a gene without introns.
-
(a)
-
(3)
From the 1410 sequences resulting from the above the following further discards were made:
-
(a)
any sequence whose coding segment did not start with the start codon ATG,
-
(b)
any sequence whose coding segment did not end with a stop codon (TAA, TAG, TGA) ,
-
(c)
any sequence whose coding segment was not a multiple of 3 in length,
-
(d)
any sequence with any intron not beginning with GT and/or ending with AT (sic) ,
-
(e)
any sequence whose coding segment contained an inframe stop codon.
-
(a)
-
(4)
The following additional discards were made:
-
(a)
sequences for immunoglobulins, histocompatibility antigens, and additional pseudogenes not discarded using previous criteria,
-
(b)
3 sequences longer than 50,000?bp.
-
(a)
-
(5)
One final selection was made from the sequences surviving the above in that the sequence's date of entry postdated release 74 of Genbank (January, 1993) —intended as such to minimize the overlap of the resulting test set with training sets for the programs tested in [16].
As mentioned previously, because the training and testing sets were identical in our case, or close to identical in the Burset and Guigó study [14, 16], we consider the ALLSEQ results as a brute force parameter search yielding what to expect in the ideal case and not necessarily a valid test of prediction performance. (The authors in [16] separate the test set from the training set by a date of entry criterion, but there was significant overlap between the testing and training datasets obtained [14], an inevitable overlap since the ALLSEQ dataset consisted of the "vast majority" of vertebrate sequences available at the time). We compare our initial test results with those reported by Burset and Guigó for this reason.
Early gene finding efforts are described in [37–39]. The authors of [14] provide an informative discussion, and references, on exon and intron durations, among other things. In [37], the authors observe "that the in-phase hexamer measure, which measures the frequency of occurrence of oligonucleotides of length six in a specific reading frame, is the most effective" for inclusion in gene finding. Moreover, those authors assembled their own test dataset, called HMR195 [40], based on sequences submitted to Genbank after August 1997. We proceed with the results of the clique-parameter search using the ALLSEQ dataset. The ALLSEQ dataset properties are summarized in Table 1.
3.1.1. Fivefold Cross-Validation on Single Encoding (Nonalternatively Spliced) Regions of Chromosomes I–V of C. elegans
The data for chromosomes I–V of C. elegans were obtained from release WS200 of Wormbase [41]. We note that the sixth and final chromosome of C. elegans, designated for legacy reasons as chromosome X, was excluded from this analysis as it is known to have substantial differences in gene encoding properties as compared to chromosomes I–V.
The following steps were used in order to prepare the data (described in Tables 2 and 3) prior to training and testing.
-
(1)
The data was scanned for inframe stops, and ultimately no inframe stops were detected.
-
(2)
The data was scanned for alternative splicing, and 6260 (30.5%) out of a total of 20514 sequences represent alternative splicing—including some forward encoded alternative splicings overlapping with reverse encoded alternative splicings.
-
(3)
In order to avoid the complexities involved in the prediction of alternative splicings, the transitive closure with respect to overlap of all alternative splicings was deleted from the data, and the remaining annotation was appropriately offset in compensation for the deletions. For all branches of all alternative splicing sequences—along with any sequences interfering with them—the following segments, s, were deleted:
-
(a)
s = the 5'-UTR, where (15?b < length(s) = 200?b) (15 = WS/2: see item 7 below) ,
-
(b)
s = the 3'-UTR, where (15?b < length(s) = 3?kb) ,
-
(c)
s = the entire coding sequence, CDS, including exons and introns.
-
(a)
-
(4)
In order to avoid both the complexity of segmented prediction as well as any bias toward any specific subset of chromosomes during cross-validation, the following were performed:
-
(a)
both data and annotation files for all 5 chromosomes were divided into a total of 67 autonomous chunks of nominal size 1?Mb and minimum size 500?kb,
-
(b)
the resulting 67 chunks were then evenly (as allowable) distributed into five (5) groups for 5-fold cross-validation.
-
(a)
-
(5)
Training was performed independently on each of the above chunk groups with a sampling window size of first WS = 30, then WS = 40.
-
(6)
Fivefold cross-validation counts from training on chunk groups 1–4 were combined to form probability estimates used to test on chunk group 5, then training on 2–5 for testing on 1, and so on.
3.2. Application of Metastate HMM Model to the Test Data
The metastate HMM is higher order in both base-emission Markov order and state-transition Markov order, that is, the metastate HMM describes an irreducible joint-probability, or "clique," generalization. The footprint states created from windows of 13 primitive states (or footprint size  , in consecutive overlapping "dimers") lead to one of our best performing models, with full-exon predictive accuracy of 86% on the B&G ALLSEQ data [16] (with data used as both train and test for comparison with GeneID+ and FGENEH). One method, FGENEH, is similar to ours in that it only uses the intrinsic genomic sequence data (not homology searches, etc.). FGENEH's predictive accuracy on the same ALLSEQ data was 64% [16]. One of the best scoring methods on the ALLSEQ data is GeneID+, whose accuracy is 71%, where GeneID+ does use external information [16]. The base-level accuracy of our metastate HMM on the ALLSEQ data is 97%, compared to 86% scoring at the full-exon correct level, indicating that improvement in identification of coding/noncoding transitions would improve results, particularly at start of coding. This has been addressed in [17] with the introduction of SVM methods so will not be elaborated upon here. Further efforts to merge the SVM sensor into the metastate HMM are described in the Discussion.
, in consecutive overlapping "dimers") lead to one of our best performing models, with full-exon predictive accuracy of 86% on the B&G ALLSEQ data [16] (with data used as both train and test for comparison with GeneID+ and FGENEH). One method, FGENEH, is similar to ours in that it only uses the intrinsic genomic sequence data (not homology searches, etc.). FGENEH's predictive accuracy on the same ALLSEQ data was 64% [16]. One of the best scoring methods on the ALLSEQ data is GeneID+, whose accuracy is 71%, where GeneID+ does use external information [16]. The base-level accuracy of our metastate HMM on the ALLSEQ data is 97%, compared to 86% scoring at the full-exon correct level, indicating that improvement in identification of coding/noncoding transitions would improve results, particularly at start of coding. This has been addressed in [17] with the introduction of SVM methods so will not be elaborated upon here. Further efforts to merge the SVM sensor into the metastate HMM are described in the Discussion.
Other gene finding methods typically involve some degree of preprocessing—as is made clear by how their test-data is often arranged (e.g., the 570 separate sequences, each containing one gene, in the B&G ALLSEQ dataset [16]). When examining these datasets, and then turning to applying our methods on large blocks of genomic data, there seems to be a "contrast" problem in the recognition of the start-of-coding region when working with the standard 1st order HMM (a "needle-in-the-haystack" problem). We find in our metastate HMM approach that the contrast problems are automatically solved, and that many of the beneficial attributes of HMM-with-duration modeling are, remarkably, recovered (the heavy-tail modeling capability on intron and exon length distributions in particular).
In this effort, we also wanted to introduce a new dataset that minimally alters the full genome dataset. We want our optimized HMM to also lay the foundation for a multifaceted regulatory motif discovery process. The gene prediction, in the end, will not only identify gene structure, but it will have done so by identifying similar structures and regions in relation to the eij-transitions. The regions around the predicted eij-transitions can, thus, be analyzed using focused motif-finder approaches (like the MI method in [27, 28], to then decipher various aspects of gene-regulation). To this end, our main concern with the raw C. elegans genomic data is that the alternatively spliced regions will be harder for the HMM to manage, since it is not part of the modeling in any way, and will be harder to score, since one prediction will exclude an overlapping alternatively spliced variant, such that to be correct on one you have to be wrong on the other. So our approach is to simply drop the regions of the genome that have alternatively splice genes. More precisely, we drop those segments of the genome corresponding to the transitive closure with respect to overlap of alternatively spliced genes. The alternatively-spliced regions are simply dropped from the working dataset (resulting in dataset C. elegans reduced), and the annotation is offset as needed to compensate for the deletions. The alt-splice redacted set of genomic data that we obtain is reduced by 30.5% for chromosomes I–V (C. elegans genome release WS200). We make no use of the sixth chromosome (labeled as X, roman numeral ten, for legacy reasons), where the odd naming convention is the least of the oddities of this chromosome, which has a large contribution from nonprotein encoding DNA (tRNA, etc.).
Our alternative-splice redacted C. elegans genome has chromosomes I–V concatenated, then it splits into 67 nonoverlapping chunks, which are then evenly distributed (as allowable) amongst five groups ("folds"). Fivefold cross-validation was then performed where 4 folds are used in learning the HMM parameters, and the other fold used to test, with prediction scored against the annotation on that fold, and this process was repeated with other folds held out, then it was averaged over all five cross-validations to obtain the prediction accuracies detailed in the Results. On the alt-splice redacted genome, we have a full-exon prediction accuracy of 74% (with  ), while the
), while the  model, with minimal footprint, has full-exon predictive accuracy of only 61%, in rough agreement with the performance of standard-HMM gene finders with purely intrinsic information (like FGENEH). The base level accuracy at
model, with minimal footprint, has full-exon predictive accuracy of only 61%, in rough agreement with the performance of standard-HMM gene finders with purely intrinsic information (like FGENEH). The base level accuracy at  is 90%, so as with the ALLSEQ data, there is clear room for improvement with better eij-transition recognition. Further details are left to Section 4, along with Sections 5 and 6. In Section 3, we describe (i) dataset preparation; (ii) generalized HMMs; (iii) the generalized footprint state structure for gene finding; (iv) the measures of accuracy used. In the Background that follows, we describe (i) the data to be analyzed; (ii) HMMs; (iii) HMMs with state structure for gene finding.
is 90%, so as with the ALLSEQ data, there is clear room for improvement with better eij-transition recognition. Further details are left to Section 4, along with Sections 5 and 6. In Section 3, we describe (i) dataset preparation; (ii) generalized HMMs; (iii) the generalized footprint state structure for gene finding; (iv) the measures of accuracy used. In the Background that follows, we describe (i) the data to be analyzed; (ii) HMMs; (iii) HMMs with state structure for gene finding.
3.3. The Generalized-Clique HMM Construction
The traditional HMM assumes that a 1st order Markov property holds among the states and that each observable depends only on the corresponding state and not any other observable. The current work entails a maximally interpolated departure from that convention (according to training dataset size) in an attempt to leverage anomalous statistical information in the neighborhood of coding-noncoding transitions (e.g., the exon-intron, introns-exon, junk-exon, or exon-junk transitions, collectively denoted as "eij-transitions"). The regions of anomalous statistics are often highly structured, having consensus sequences that strongly depart from the strong independence assumptions of the 1st order HMM. The existence of such consensus sequences suggests that we adopt an observation model that has a higher order Markov property with respect to the observations. Furthermore, since the consensus sequences vary by the type of transition, this observational Markov order should be allowed to vary depending on the state.
In the Viterbi context, for a given state dimer transition, such as e 0 e 1 or e 0 i 0, we can boost the contributions of the corresponding base emissions to the correct prediction of state by using extended states. Specifically, when encountered sequentially in the Viterbi algorithm, the sequence of eij-transition footprint states would conceivably score highly when computed for the footprint-width number of footprint states that overlap the eij-transition (as the generalized clique is moved from left to right over the HMM graphical model, as shown in Figure 1). In other words, we can expect a natural boosting effect for the correct prediction at such eij-transitions (compared to the standard HMM).
(a) sliding-window association (clique) of observations and hidden states in the metastate hidden Markov model, where the clique-generalized HMM algorithm describes a left-to-right traversal (as is typical) of the HMM graphical model with the specified clique window. The first observation,  , is included at the leading edge of the clique overlap at the HMM's left boundary. For the last clique's window overlap, we choose the trailing edge to include the last observation
, is included at the leading edge of the clique overlap at the HMM's left boundary. For the last clique's window overlap, we choose the trailing edge to include the last observation  . (b) graphical model of the clique-generalized HMM, where the interconnectedness on full joint dependencies is only partly drawn. The graphical model is significantly constrained, as well, in a manner not represented in the graphical model, in that state sequences are only allowed with at most one nonself transition.
. (b) graphical model of the clique-generalized HMM, where the interconnectedness on full joint dependencies is only partly drawn. The graphical model is significantly constrained, as well, in a manner not represented in the graphical model, in that state sequences are only allowed with at most one nonself transition.
The metastate, clique-generalized HMM entails a clique-level factorization rather than the standard HMM factorization (that describes the state transitions with no dependence on local sequence information). This is described in the general formalism to follow, where specific equations are given for application to eukaryotic gene structure identification.
Observation and state dependencies in the generalized-clique HMM are parameterized independently according to the following.
-
(1)
Nonnegative integers
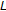 and
and  denoting left and right maximum extents of a substring,
denoting left and right maximum extents of a substring, 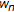 , (with suitable truncation at the data boundaries,
, (with suitable truncation at the data boundaries,  and
and  ) are associated with the primitive observation,
) are associated with the primitive observation,  , in the following way:
, in the following way: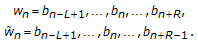 (4)
(4) -
(2)
Nonnegative integers
 and
and  are used to denote the left and right extents of the extended (footprint) states,
are used to denote the left and right extents of the extended (footprint) states,  . Here, we show the relationships among the primitive states
. Here, we show the relationships among the primitive states 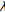 , dimer states
, dimer states  , and footprint states
, and footprint states 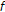 ,
, (5)
(5) (6)
(6)
As in the 1st order HMM, the  th base observation
th base observation  is aligned with the nth hidden state
is aligned with the nth hidden state  .
.
With the choice of first and last clique described in Figure 1, we have introduced some additional state and observation primitives (associated with unit-valued transition and emission probabilities) for suitable values of  ,
,  ,
,  , and
, and  . These additional primitives are shown in Table 4.
. These additional primitives are shown in Table 4.
Given the above, the clique-factorized HMM is as follows:

A generalization to the Viterbi algorithm can now be directly implemented, using the above form, to establish an efficient dynamic programming table construction. Generalized expressions for the Baum-Welch algorithm are also possible. Some of the generalizations are straightforward extensions of the algorithms from 1st order theory with its minimal clique. Sequence-dependent transition properties in the generalized-clique formalism have no counterpart in the standard 1st order HMM formalism, however, and that will be elaborated upon here.
The core term in the clique-factorization is

In the standard Markov model,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  :
:

In the above, we introduce the constraint notation with the vertical bar notation, where the expression on the left is the clique factorization term with the constraint that it approximates according to the standard HMM conditional probabilities.
The core term in the clique factorization can also be written by introducing a Bayesian parameter, one that happens to provide a matching joint probability construct (to the extent possible) with the term in the numerator

We now examine specific cases of this equation to clarify the novel improvements that result. In what follows, we constrain our model to have a minimum length on regions (thus self-transitions), such that footprint states, and their transitions, can only have one transition between different states.
Consider the case with the first footprint state being of eij-transition type, and the second footprint thereby constrained to be of the appropriate xx-type

where use is made of the relation  for the unique xx-footprint that follows the eij-transition given our minimum length constraint.
for the unique xx-footprint that follows the eij-transition given our minimum length constraint.
Consider, next, the case with the first footprint state being xx-type,

If the second footprint is eij-transition type, then the equation has two sum terms in the denominator if the first transition is ii or jj transition, and a third sum contribution (the term with " ") if the first transition is an ee-transition:
") if the first transition is an ee-transition:
In what follows, dimer notation is used on footprints, since we are interested in the footprint-to-footprint transitions. Given their large overlap dependence, this notation and formalism directly generalizes to the same cases no matter the size of the footprint (due to the single major-transition in or between footprints constraint that is provided by a minimum length constraint).
If  we have three cases:
we have three cases:  . For
. For  , we have two possible
, we have two possible  ; for
; for  , we have two possible
, we have two possible  ; for
; for  , we have three possible
, we have three possible  .
.

where we have introduced the notation "ii" to denote the dimer state or the footprint state "ii⋯ iii," and the notation "ie" to denote the dimer state or the footprint state "ii⋯ iie",
Similarly, consider  and
and 

For the  and
and  , we get a similar expression, but a third term in the sum due to the three possibilities allowed for
, we get a similar expression, but a third term in the sum due to the three possibilities allowed for  ,
,

Likewise for the  and
and  , we get a similar expression, but a third term in the sum
, we get a similar expression, but a third term in the sum

Consider now the cases involving self-transitions:  and
and  . The derivation parallels that are above for
. The derivation parallels that are above for  and
and  ,
,

Similarly, consider  and
and  ,
,

For the  and
and  , we get the third term in the sum due to the three possibilities allowed for
, we get the third term in the sum due to the three possibilities allowed for  ,
,

In the above expressions, we clearly have sequence-dependent transitions. For  and
and  for example, we have
for example, we have

while the standard HMM has this ratio with  a single element emission sequence, and
a single element emission sequence, and  =
=  , thus, for the standard HMM,
, thus, for the standard HMM,

If we generalized the std. HMM to higher order Markov models on emissions, to the same order as in the generalized clique, there is still the difference in the transition probability contributions

as can be seen in the ratio of their contributions, and how it is sequence dependent (i.e., dependent on " ")
")

Note that the sequence dependencies (in this and the other footprint transition choices) enter via likelihood ratio terms. These are precisely the type of terms examined in [17] in an effort to improve the HMM-based discriminatory ability via use of SVMs. The "discriminatory" aspect of the key new (sequence-dependent) contribution is most evident in forms like that above, where we have a likelihood ratio for the observed sequences given the different label "classifications" chosen. In the cases that follow, we will examine the extreme cases of the likelihood-ratio discriminator strongly classifying one way or the other, or not strongly classifying either way with the given sequence information (making the contribution of knowing that sequence information negligible, which should then reduce to the std. HMM situation, as will be shown). Specifically, we will now examine the above equations in situations where the sequence-dependent likelihood ratios strongly favor one state model over another, with particular attention as to whether there are sequence-dependent scenarios offering recovery of the heavy-tail distribution in example one and recovery of contrast resolution in example two.
Example 1.
For  and
and  , we showed
, we showed

Case 1.
 (likelihood ratio of probabilities is approximately one, leading to a weak (small) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)
(likelihood ratio of probabilities is approximately one, leading to a weak (small) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)

Thus, in the "uninformed" case we recover regular 1st order HMM theory, with geometric distribution on "ii." In this notation,  refers to the value of
refers to the value of  when the observed sequence
when the observed sequence  has approximately the same probability regardless of the state being "ii" or "ie."
has approximately the same probability regardless of the state being "ii" or "ie."
Case 2.
 (likelihood ratio of probabilities is very large, leading to a strong (large) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)
(likelihood ratio of probabilities is very large, leading to a strong (large) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)

In this case, we obtain contributions less than the regular 1st order HMM counterpart, effectively shortening the geometric distribution on "ii" → for example, it adaptively switches to a shorter, sharper falloff on the distribution in a sequence-dependent manner.
Case 3.
 (likelihood ratio of probabilities is very small, leading to a strong (large) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)
(likelihood ratio of probabilities is very small, leading to a strong (large) classification confidence if a confidence parameterized classifier, like an SVM, is referred to in place of the simple ratio)

In this case, we obtain contributions greater than the regular 1st order HMM theory. In particular, we recover the heavy-tail distribution in a sequence-dependent manner

Example 2.
One more example case will be considered, that is involving acceptor splice-site recognition. For  , and
, and  , we have
, we have

Case 1.


We recover regular HMM theory in the uninformed situation.
Case 2.


Greater than regular 1st order HMM theory removes key penalty of  factor when sequence match overrides and resolves weak contrast resolution at 1st order.
factor when sequence match overrides and resolves weak contrast resolution at 1st order.
Case 3.


Less than regular 1st Order HMM effectively weakens ie transition strength (the classic major-transition bias factor).
The clique factorization also allows for an alternate representation such that the internal scalar-based state discriminant can be replaced with a vector-based feature. This would allow the substitution of a discriminant based on a support vector machine (SVM) as demonstrated for splice sites in [17]. Also, we note that these alternate representations would not introduce any significant increase in computational complexity, since the SVM-based discriminant, having been trained offline, would require the computation of a simple vector dot product. Thus, the likelihood ratio lookup can simply be to the tabulated sequence probability estimates (based on counts, as outlined in what follows) or make use of BLAST (homology-based) test, or an SVM-based test (the latter two cases areas of ongoing work, see Section 5).
3.4. Enumeration of the Footprint States
According to the restrictions just described, footprint states fall into the same two categories or types as dimer states, xx-type and eij-type. Regardless of footprint state type, each footprint state can be considered to be generated by the xx-type dimer that it contains. For xx-types, it is sufficient to specify the generating dimer only, such as i 0 i 0 for the xx-type footprint state i 0 i 0⋯ i 0. For eij-types, a position must also be specified for the location of the generating dimer within the generated footprint state. The number of xx-type footprint states is identical to the number of xx-type dimers, as enumerated in Table 5.
As for the eij-type footprint states, each is generated by the nonhomogeneous dimer that it contains but is further characterized by the position of the generating dimer within the footprint string, such as e 0 i 0 in the right-most position of the eij-type footprint state e (F−2)mod3 e (F−1)mod3⋯ e 0 e 0 e 0 i 0. As a consequence of this, there are  eij-type footprint states for each corresponding eij-type dimer. Given an eij-type footprint state of length
eij-type footprint states for each corresponding eij-type dimer. Given an eij-type footprint state of length  in dimers, there are precisely
in dimers, there are precisely  possible positions for the implied eij-type dimer to occur within the footprint state's string of primitives. These dimer positions are labeled
possible positions for the implied eij-type dimer to occur within the footprint state's string of primitives. These dimer positions are labeled  and taken in the order of encoding (forward or reverse) in Table 6. Thus we have the relation: no. of eij-type footprint states =
and taken in the order of encoding (forward or reverse) in Table 6. Thus we have the relation: no. of eij-type footprint states =  = (no. of eij-type dimer states)
= (no. of eij-type dimer states)  .
.
We have the following relations:
no. of footprint states  ,
,
no. of footprint state transitions  .
.
In the model without the minimum length constraint, we still have the fundamental set of 33 dimers, beyond that, however, the larger footprints can have arbitrary numbers of state toggles
no. of extended states without minimum length assumption  ,
,
no. of extended state transitions without minimum length assumption  .
.
3.5. Measures of Predictive Performance That Are Used
The measure of prediction performance was taken in two ways: full exon accuracy and individual base (nucleotide) accuracy, according to the conventions of Burset and Guigó in [16].
Accuracy at the base or nucleotide level is given by

where

Note that the authors [16] have used an alternative form of specificity from the usual form

This is done in the context of gene prediction, with typically high concentrations of junk, where the contribution from the quantity TN = true negative (or correctly predicted actual noncoding) can overwhelm FP in what is actually weakly accurate prediction (i.e., scoring is best conveyed in terms of the overlap between predicted positives and actual positives [42]).
We use  for accuracy, following the conventions of [16], partly to compare with their results, but we also calculate the specificity according to the standard form
for accuracy, following the conventions of [16], partly to compare with their results, but we also calculate the specificity according to the standard form  , and both of these values are shown in Tables 9 and 10. The specificity convention
, and both of these values are shown in Tables 9 and 10. The specificity convention  has the effect of weighting genes with shorter and fewer exons more heavily in the base and exon level accuracy measurements, respectively. (In the notation to follow, sp will be used in place of sp* if there is no ambiguity.) Moreover, this effect can become extremely pronounced in cases such as both of the cited evaluations, where all DNA sequences tested contain only a single gene. In this effort, the number of correct (and incorrect) predictions is first summed over all test sequences, and then the measurements were computed from those sums for the exon and base level measurements, respectively. Either method of measurement appears appropriate for the Burset and Guigó datasets, where the data sequences have a single gene via preprocessing (and may be leveraged as such in the design of the program being tested). In what is a more realistic context of raw genomic data processing, however, we are likely to encounter two key issues as part of the problem
has the effect of weighting genes with shorter and fewer exons more heavily in the base and exon level accuracy measurements, respectively. (In the notation to follow, sp will be used in place of sp* if there is no ambiguity.) Moreover, this effect can become extremely pronounced in cases such as both of the cited evaluations, where all DNA sequences tested contain only a single gene. In this effort, the number of correct (and incorrect) predictions is first summed over all test sequences, and then the measurements were computed from those sums for the exon and base level measurements, respectively. Either method of measurement appears appropriate for the Burset and Guigó datasets, where the data sequences have a single gene via preprocessing (and may be leveraged as such in the design of the program being tested). In what is a more realistic context of raw genomic data processing, however, we are likely to encounter two key issues as part of the problem
-
(1)
we have raw genomic sequences that contain multiple genes:
-
(2)
scoring at the exon level in effect designates the exon as the fundamental unit being counted rather than the gene, this avoids weighing more complex genes the same as simpler genes (that have fewer exons).
As indicated above, in each case of the datasets used in this effort, the measurements for both the exon and base level prediction differ somewhat from the method used in the cited evaluations. Moreover, of the datasets tested in this effort, ALLSEQ is the only dataset consisting entirely of single-gene DNA sequences. The results of the metastate HMM for ALLSEQ in this effort are given in both the cited measure of accuracy [6] as well as standard "exon-level" scoring.
The accuracy measure at the full-exon level presents a much greater challenge as it requires the successful prediction of the entire exon for the exon to be scored as correct. These events include the start and end positions of exons as well as the continuation of the exon at all intermediate introns splicing points. The full-exon accuracy is given similar to that given before at base-level scoring

where

Again, SP will be used in place of SP* in what follows if there is no ambiguity. It should be noted that this measure for full-exon accuracy does not allow for any improvement due to partial exon prediction. More specifically, the exon level accuracy can only be improved by the precise prediction of one or more entire exons—at both start and end positions.
4. Results
All predictions are based on state prior, state transition, and emission probabilities which are estimated directly from counts in the training data without any further refinement. The metastate HMM model is interpolated to highest Markov order on emission probabilities given the training data size, and to highest Markov order (subsequence length) on the footprint states (with different values shown in the Results as multitrajectory plots). The former is accomplished via simple count cutoff rules, the latter via an identification of anomalous base statistics near the coding/noncoding transitions, initially, followed by direct HMM performance tuning. Allowed footprint transitions are restricted to those that have at most one coding/noncoding transition, which leads to only linear growth in state number with footprint size,not geometric growth, enabling the full advantage of generalized-clique modeling at a computational expense little more than that of a standard HMM.
4.1. Algorithmic Complexity of Meta-HMM Dynamic Programming Table Construction
For comparison with the metastate HMM, we first consider the complexity of the traditional 1st order HMM. First, define " " as the length of the testing dataset and "
" as the length of the testing dataset and " " as the number of states. The Viterbi algorithm constructs the table recursively, with computational updates in each cell in a given column only dependent on computations involving each of the cells of the prior column; thus, the time complexity involved in the Viterbi algorithm is given by
" as the number of states. The Viterbi algorithm constructs the table recursively, with computational updates in each cell in a given column only dependent on computations involving each of the cells of the prior column; thus, the time complexity involved in the Viterbi algorithm is given by  . In the metastate HMM, we have similar growth in number of states, but in the case of the increasing footprint size
. In the metastate HMM, we have similar growth in number of states, but in the case of the increasing footprint size  , this increase in states, and state transitions, is linear, with time complexity given by
, this increase in states, and state transitions, is linear, with time complexity given by  , where linearity in
, where linearity in  for fixed
for fixed  and
and  is verified in the set of time trials shown in Figure 2.
is verified in the set of time trials shown in Figure 2.
4.2. Results for Benchmark Dataset ALLSEQ
Exon- and base-level accuracy for values of the parameters  ,
, ,
, , and
, and  were tested and examined for stability. Figures 3 and 4 below show plots for exon- and base-level maxima, respectively, over the parameters
were tested and examined for stability. Figures 3 and 4 below show plots for exon- and base-level maxima, respectively, over the parameters  and
and  of metastate HMM's prediction performance. The plots illustrate the enhanced performance of the metastate HMM over simpler prediction models, including the (null hypothesis result) metastate HMM for which the base Markov parameter
of metastate HMM's prediction performance. The plots illustrate the enhanced performance of the metastate HMM over simpler prediction models, including the (null hypothesis result) metastate HMM for which the base Markov parameter  . (Note: the metastate HMM uses only the intrinsic information in the data making no use of extrinsic information, such as ESTs, protein homology, etc.)
. (Note: the metastate HMM uses only the intrinsic information in the data making no use of extrinsic information, such as ESTs, protein homology, etc.)
In comparing the results of this dataset to the other results in this effort, the quality of the best result can be attributed to the increased size of the training dataset (despite the decreased coding density) as well as adherence among the donor and acceptor splice sites to the consensus sequences, gt and ag, respectively. Figures 3 and 4 also show the best performing predictors from the original benchmark study, FGENEH and GeneID+, that use intrinsic and extrinsic genomic information, respectively. At both the full-exon and base levels, the metastate HMM outperforms standard HMM approaches by a discernable margin.
4.3. Results for C. elegans Dataset
The results shown in Figures 5 and 6 indicate that a local maximum for the exon and base level predictions was attained at  , with a plateau for
, with a plateau for  extending to
extending to  , with exact exon prediction accuracy 74% and base accuracy 90%. In comparing the results of this dataset to the other results in this effort, the reduced performance at full-exon level for
, with exact exon prediction accuracy 74% and base accuracy 90%. In comparing the results of this dataset to the other results in this effort, the reduced performance at full-exon level for  compared to that for
compared to that for  is an indication of insufficient training size reflected in lack of support for
is an indication of insufficient training size reflected in lack of support for  probability estimates at splice sites.
probability estimates at splice sites.
The degree of preconditioning in our dataset is minimal, such that there is allowance in the data for disagreement with the consensus dinucleotide introns sequences, gt and ag, as well as the incorporation of reverse encodings. As mentioned previously, we arrive at a base accuracy of 90%. The prospects for improving this result further are many, starting with simply enlarging the training dataset by including similar genomes from other nematodes, C. briggsiae in particular (see further discussion in Section 6).
5. Discussion
The top performing results from the evaluations performed in [14, 16] are included in Tables 7 and 8 (where they predict on data that has much greater preprocessing, not raw genome), including values for the (nucleotide) base level accuracy converted from the AC measurement to E[(sn + sp)/2].
Table 9 shows the top results of the metastate HMM for the datasets and parameter values tested in this effort, including in each case the optimum values for the parameters  ,
,  ,
,  , and
, and  . Recall that the method of measurement used in this effort differs slightly from that of the cited evaluations. For additional reference, Table 10 shows the maximum accuracy specifically for the ALLSEQ dataset at both the base and exon levels using the method of measurement in the cited evaluations, as well as our own.
. Recall that the method of measurement used in this effort differs slightly from that of the cited evaluations. For additional reference, Table 10 shows the maximum accuracy specifically for the ALLSEQ dataset at both the base and exon levels using the method of measurement in the cited evaluations, as well as our own.
The metastate HMM's performance on the ALLSEQ dataset clearly exceeds that of the top performing program, GeneID+, cited in [16], by substantial margins, 6.5% and 17%, at the base and exon levels, respectively. GeneID+ also uses extrinsic information via "amino acid similarity searches" in the process of forming its prediction, whereas the metastate HMM in this effort uses only the intrinsic information contained in the DNA sequence data alone.
The question naturally arises on how we might do better, and we are proceeding in three directions: (1) verifying that HMMD offers little improvements due to the recovery of the heavy tail attribute see [24]; (2) future work involving pMM/SVM sensors [17]; (3) future work involving alternative-splice state structures [43] (with verification of statistical support for the more elaborate state model indicated in [27]); (4) use of large footprints of HMMD scaffolding to employ zone-dependent statistics to capture cis-regulatory signaling, in particular, in the generalized meta-HMMD model. In this effort, we tried to mainly draw comparisons with other methods similarly based solely on intrinsic genomic statistics. The method presented here will benefit from extrinsic genomic information "addons" for boosting performance via use of homology matching, or EST alignment, for example. We do not compare with the state-of-the-art extrinsic/intrinsic techniques in this purely intrinsic approach, but upon the further extrinsic/intrinsic statistical modeling refinements indicated above, such a comparison will be made and judging from the performance of the meta-HMM modeling foundation, a state-of-the-art gene structure identifier should result.
6. Conclusion
We describe a clique-generalized, metastate HMM. The model involves both observations and states of extended length in a generalized-clique structure, where the extents of the observations and states are incorporated as parameters in the new model. This clique structure was intended to address the following 2-fold hypothesis.
-
(1)
The introduction of extended observations would take greater advantage of the information contained in higher order, position-dependent, signal statistics in DNA sequence data taken from extended regions surrounding coding/noncodong sites.
-
(2)
The introduction of extended states would attain a natural boosting by repeated lookup of the tabulated statistics associated in each case with the given type of coding/noncoding boundary.
We find that our metastate HMM approach enables a stronger HMM-based framework for the identification of complex structure in stochastic sequential data. We show an application of the metastate HMM to the identification of eukaryotic gene structure in the C. elegans genome. We have shown that the performance of the metastate HMM-based gene finder performs comparably to three of the best gene finders in use today, GENIE, GENSCAN, and HMMgene [44]. The method shown here, however, is the bare-bones HMM implementation without use of signal sensors to strengthen localized encoding information, such as splice site information. An SVM-based improvement, to integrate directly with the approach introduced here, is described in [17], and given the successful use of neural-net discriminators to improve splice-site recognition in the GENIE gene finder [45], there are clear prospects for further improvement in overall gene-finding accuracy with the metastate HMM foundation described in this paper.
References
Stanke M, Morgenstern B: AUGUSTUS: a web server for gene prediction in eukaryotes that allows user-defined constraints. Nucleic Acids Research 2005, 33(2):W465-W467.
Rajapakse JC, Ho LS: Markov encoding for detecting signals in genomic sequences. IEEE/ACM Transactions on Computational Biology and Bioinformatics 2005, 2(2):131-141. 10.1109/TCBB.2005.27
Majoros WH, Pertea M, Salzberg SL: TigrScan and GlimmerHMM: two open source ab initio eukaryotic gene-finders. Bioinformatics 2004, 20(16):2878-2879. 10.1093/bioinformatics/bth315
Taher L, Rinner O, Garg S, Sczyrba A, Brudno M, Batzoglou S, Morgenstern B: AGenDA: homology-based gene prediction. Bioinformatics 2003, 19(12):1575-1577. 10.1093/bioinformatics/btg181
Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ: Basic local alignment search tool. Journal of Molecular Biology 1990, 215(3):403-410.
Sonnenburg S, Zien A, Rätsch G: ARTS: accurate recognition of transcription starts in human. Bioinformatics 2006, 22(14):e472-e480. 10.1093/bioinformatics/btl250
Do JH, Choi DK: Computational approaches to gene prediction. Journal of Microbiology 2006, 44(2):137-144.
Korf I: Gene finding in novel genomes. BMC Bioinformatics 2004., 5, article 59:
Mathé C, Sagot MF, Schiex T, Rouzé P: Current methods of gene prediction, their strengths and weaknesses. Nucleic Acids Research 2002, 30(19):4103-4117. 10.1093/nar/gkf543
Allen JE, Majoros WH, Pertea M, Salzberg SL: JIGSAW, GeneZilla, and GlimmerHMM: puzzling out the features of human genes in the ENCODE regions. Genome Biology 2006, 7(supplement 1):S9.
Noguchi H, Park J, Takagi T: MetaGene: prokaryotic gene finding from environmental genome shotgun sequences. Nucleic Acids Research 2006, 34(19):5623-5630. 10.1093/nar/gkl723
Taher L, Rinner O, Garg S, Sczyrba A, Brudno M, Batzoglou S, Morgenstern B: AGenDA: homology-based gene prediction. Bioinformatics 2003, 19(12):1575-1577. 10.1093/bioinformatics/btg181
van Baren MJ, Koebbe BC, Brent MR: Using N-SCAN or TWINSCAN to predict gene structures in genomic DNA sequences. Current Protocols in Bioinformatics 2007., (chapter 4, unit 4.8):
Rogic S, Mackworth AK, Ouellette FBF: Evaluation of gene-finding programs on mammalian sequences. Genome Research 2001, 11(5):817-832. 10.1101/gr.147901
Dunham I, Shimizu N, Roe BA, Chissoe S: The DNA sequence of human chromosome 22. Nature 1999, 402(6761):489-495. 10.1038/990031
Burset M, Guigó R: Evaluation of gene structure prediction programs. Genomics 1996, 34(3):353-367. 10.1006/geno.1996.0298
Roux B, Winters-Hilt S: Hybrid MM/SVM structural sensors for stochastic sequential data. BMC Bioinformatics 2008, 9(supplement 9):S12.
Liu H, Han H, Li J, Wong L: DNAFSMiner: a web-based software toolbox to recognize two types of functional sites in DNA sequences. Bioinformatics 2005, 21(5):671-673. 10.1093/bioinformatics/bth437
Sonnenburg S, Schweikert G, Philips P, Behr J, Rätsch G: Accurate splice site prediction using support vector machines. BMC Bioinformatics 2007., 8(supplement 10, article S7):
Degroeve S, Saeys Y, De Baets B, Rouzé P, Van de Peer Y: SpliceMachine: predicting splice sites from high-dimensional local context representations. Bioinformatics 2005, 21(8):1332-1338. 10.1093/bioinformatics/bti166
Muro EM, Herrington R, Janmohamed S, Frelin C, Andrade-Navarro MA, Iscove NN: Identification of gene 3′ ends by automated EST cluster analysis. Proceedings of the National Academy of Sciences of the United States of America 2008, 105(51):20286-20290. 10.1073/pnas.0807813105
Bellora N, Farré D, Albà MM: PEAKS: identification of regulatory motifs by their position in DNA sequences. Bioinformatics 2007, 23(2):243-244. 10.1093/bioinformatics/btl568
He X, Ling XU, Sinha S: Alignment and prediction of cis-regulatory modules based on a probabilistic model of evolution. PLoS Computational Biology 2009, 5(3):1-14.
Winters-Hilt S, Jiang Z: Hidden Markov model with duration side-information for novel HMMD derivation, with application to eukaryotic gene finding. EURASIP Genome Signal Processing. In press
Winters-Hilt S, Baribault C: A novel, fast, HMM-with-Duration implementation—for application with a new, pattern recognition informed, nanopore detector. BMC Bioinformatics 2007, 8(7, article S7):S19. 10.1186/1471-2105-8-S7-S19
Winters-Hilt S, Jiang Z: A hidden markov modelwith binned duration algorithm. IEEE Transactions on Signal Processing 2010, 58(2):948-952.
Winters-Hilt S: Hidden Markov model variants and their application. BMC Bioinformatics 2006, 7(2, article S2):S14. 10.1186/1471-2105-7-S2-S14
Lu D: Motif finding, UNO MS thesis in CS. 2009. Advisor—Prof. S. Winters-Hilt
Shinozaki D, Akutsu T, Maruyama O: Finding optimal degenerate patterns in DNA sequences. Bioinformatics 2003, 19(2):ii206-ii214. 10.1093/bioinformatics/btg1079
Frickey T, Weiller G: Mclip: motif detection based on cliques of gapped local profile-to-profile alignments. Bioinformatics 2007, 23(4):502-503. 10.1093/bioinformatics/btl601
de Hoon MJL, Imoto S, Nolan J, Miyano S: Open source clustering software. Bioinformatics 2004, 20(9):1453-1454. 10.1093/bioinformatics/bth078
Wang G, Yu T, Zhang W: WordSpy: identifying transcription factor binding motifs by building a dictionary and learning a grammar. Nucleic Acids Research 2005, 33(2):W412-W416.
The C. elegans Sequencing Consortium : Genome sequence of the nematode C. elegans : a platform for investigating biology. Science 282(5396):2012-2018.
Durbin R, Eddy S, Krogh A, Mitchison G: Biological Sequence Analysis, Probabilistic Models of Proteins and Nucleic Acids. 82005th edition. Cambridge University Press, Cambridge, UK; 1998.
Rabiner LR, Juang BH: INTRODUCTION TO HIDDEN MARKOV MODELS. IEEE ASSP magazine 1986, 3(1):4-16.
Genome BioInformatics Research Laboratory : Resources & datasets. October 2005, http://genome.imim.es/databases/genomics96/index.html
Fickett JW, Tung C-S: Assessment of protein coding measures. Nucleic Acids Research 1992, 20(24):6441-6450. 10.1093/nar/20.24.6441
Snyder EE, Stormo GD: Identification of protein coding regions in genomic DNA. Journal of Molecular Biology 1995, 248(1):1-18. 10.1006/jmbi.1995.0198
Fickett JW: The gene identification problem: an overview for developers. Computers and Chemistry 1996, 20(1):103-118. 10.1016/S0097-8485(96)80012-X
Rogic S: HMR195 dataset. http://www.cs.ubc.ca/~rogic/evaluation/dataset.html
WormBase : WS200. March 2009, http://www.wormbase.org
Tan PN, Steinbach M, Kumar V: Introduction to Data Mining. Pearson Education, Boston, Mass, USA; 2006.
Winters-Hilt S: Using a meta-HMM for alternative-splice gene structure identification. Paper in Preparation
du Preez JA, Weber DM: High-order hidden Markov modelling. In Proceedings of the South African Symposium on Communications and Signal Processing (COMSIG '98), September 1998, Rondebosch, South Africa. University of Cape Town; 197-202.
Reese MG, Eeckman FH, Kulp D, Haussler D: Improved splice site detection in Genie. Proceedings of the 1st Annual International Conference on Computational Molecular Biology (RECOMB '97), January 1997 232-240.
Acknowledgments
Author S. Winters-Hilt would like to thank Ph.D. Advisor David Haussler for originally posing the question of "what might be gained by use of higher-order state models?" (in a graduate bioinformatics course at UCSC in 1999). Finding the answer has taken a bit longer than expected. Both authors would also like to thank Meta Logos Inc. for allowing academic research with unrestricted use of the clique-generalized HMM software tools developed by S. Winters-Hilt while cofounding Meta Logos Inc.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Winters-Hilt, S., Baribault, C. A Metastate HMM with Application to Gene Structure Identification in Eukaryotes. EURASIP J. Adv. Signal Process. 2010, 581373 (2010). https://doi.org/10.1155/2010/581373
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/581373
 ,
, ,
,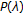 for all
for all 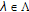 ,
,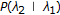 for all
for all 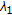
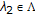 —where the standard transition probability is denoted
—where the standard transition probability is denoted 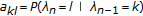 , a 1st order Markov model on states with homogenous stationary statistics (i.e., no dependence on position "
, a 1st order Markov model on states with homogenous stationary statistics (i.e., no dependence on position " "),
"), for all
for all 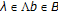 —where the standard emission probability is
—where the standard emission probability is 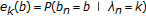 , a 0th order Markov model on bases and with homogenous stationary statistics.
, a 0th order Markov model on bases and with homogenous stationary statistics.
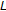 and
and  denoting left and right maximum extents of a substring,
denoting left and right maximum extents of a substring, 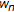 , (with suitable truncation at the data boundaries,
, (with suitable truncation at the data boundaries,  and
and  ) are associated with the primitive observation,
) are associated with the primitive observation,  , in the following way:
, in the following way: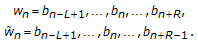
 and
and  are used to denote the left and right extents of the extended (footprint) states,
are used to denote the left and right extents of the extended (footprint) states,  . Here, we show the relationships among the primitive states
. Here, we show the relationships among the primitive states 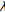 , dimer states
, dimer states  , and footprint states
, and footprint states 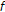 ,
,





