- Research Article
- Open access
- Published:
Shooter Localization in Wireless Microphone Networks
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 690732 (2010)
Abstract
Shooter localization in a wireless network of microphones is studied. Both the acoustic muzzle blast (MB) from the gunfire and the ballistic shock wave (SW) from the bullet can be detected by the microphones and considered as measurements. The MB measurements give rise to a standard sensor network problem, similar to time difference of arrivals in cellular phone networks, and the localization accuracy is good, provided that the sensors are well synchronized compared to the MB detection accuracy. The detection times of the SW depend on both shooter position and aiming angle and may provide additional information beside the shooter location, but again this requires good synchronization. We analyze the approach to base the estimation on the time difference of MB and SW at each sensor, which becomes insensitive to synchronization inaccuracies. Cramér-Rao lower bound analysis indicates how a lower bound of the root mean square error depends on the synchronization error for the MB and the MB-SW difference, respectively. The estimation problem is formulated in a separable nonlinear least squares framework. Results from field trials with different types of ammunition show excellent accuracy using the MB-SW difference for both the position and the aiming angle of the shooter.
1. Introduction
Several acoustic shooter localization systems are today commercially available; see, for instance [1–4]. Typically, one or more microphone arrays are used, each synchronously sampling acoustic phenomena associated with gunfire. An overview is found in [5]. Some of these systems are mobile, and in [6] it is even described how soldiers can carry the microphone arrays on their helmets. One interesting attempt to find direction of sound from one microphone only is described in [7]. It is based on direction dependent spatial filters (mimicking the human outer ear) and prior knowledge of the sound waveform, but this approach has not yet been applied to gun shots.
Indeed, less common are shooter localization systems based on singleton microphones geographically distributed in a wireless sensor network. An obvious issue in wireless networks is the sensor synchronization. For localization algorithms that rely on accurate timing like the ones based on time difference of arrival (TDOA), it is of major importance that synchronization errors are carefully controlled. Regardless if the synchronization is solved by using GPS or other techniques, see, for instance [8–10], the synchronization procedures are associated with costs in battery life or communication resources that usually must be kept at a minimum.
In [11] the synchronization error impact on the sniper localization ability of an urban network is studied by using Monte Carlo simulations. One of the results is that the inaccuracy increased significantly ( 2 m) for synchronization errors exceeding approximately 4 ms. 56 small wireless sensor nodes were modeled. Another closely related work that deals with mobile asynchronous sensors is [12], where the estimation bounds with respect to both sensor synchronization and position errors are developed and validated by Monte Carlo simulations. Also [13] should be mentioned, where combinations of directional and omnidirectional acoustic sensors for sniper localization are evaluated by perturbation analysis. In [14], estimation bounds for multiple acoustic arrays are developed and validated by Monte Carlo simulations.
2 m) for synchronization errors exceeding approximately 4 ms. 56 small wireless sensor nodes were modeled. Another closely related work that deals with mobile asynchronous sensors is [12], where the estimation bounds with respect to both sensor synchronization and position errors are developed and validated by Monte Carlo simulations. Also [13] should be mentioned, where combinations of directional and omnidirectional acoustic sensors for sniper localization are evaluated by perturbation analysis. In [14], estimation bounds for multiple acoustic arrays are developed and validated by Monte Carlo simulations.
In this paper we derive fundamental estimation bounds for shooter localization systems based on wireless sensor networks, with the synchronization errors in focus. An accurate method independent of the synchronization errors will be analyzed (the MB-SW model) as well as a useful bullet deceleration model. The algorithms are tested on data from a field trial with 10 microphones spread over an area of 100 m and with gunfire at distances up to 400 m. Partial results of this investigation appeared in [15] and almost simultaneously in [12].
The outline is as follows. Section 2 sketches the localization principle and describes the acoustical phenomena that are used. Section 3 gives the estimation framework. Section 4 derives the signal models for the muzzle blast (MB), shock wave (SW), combined MB;SW, and difference MB-SW, respectively. Section 5 derives expressions for the root mean square error (RMSE) Cramér-Rao lower bound (CRLB) for the described models and provides numerical results from a realistic scenario. Section 6 presents the results from field trials, and Section 7 gives the conclusions.
2. Localization Principle
Two acoustical phenomena associated with gunfire will be exploited to determine the shooter's position: the muzzle blast and the shock wave. The principle is to detect and time stamp the phenomena as they reach microphones distributed over an area, and let the shooter's position be estimated by, in a sense, the most likely point, considering the microphone locations and detection times.
The muzzle blast (MB) is the sound that probably most of us associate with a gun shot, the "bang." The MB is generated by the pressure depletion in effect of the bullet leaving the gun barrel. The sound of the MB travels at the speed of sound in all directions from the shooter. Provided that a sufficient number of microphones detect the MB, the shooters position can be more or less accurately determined.
The shock wave (SW) is formed by supersonic bullets. The SW has (approximately) the shape of an expanding cone, with the bullet trajectory as axis, and reaches only microphones that happens to be located inside the cone. The SW propagates at the speed of sound in direction away from the bullet trajectory, but since it is generated by a supersonic bullet, it always reaches the microphone before the MB, if it reaches the microphone at all. A number of SW detections may primarily reveal the direction to the shooter. Extra observations or assumptions on the ammunition are generally needed to deduce the distance to the shooter. The SW detection is also more difficult to utilize than the MB detection, since it depends on the bullet's speed and ballistic behavior.
Figure 1 shows an acoustic recording of gunfire. The first pulse is the SW, which for distant shooters significantly dominates the MB, not the least if the bullet passes close to the microphone. The figure shows real data, but a rather ideal case. Usually, and particularly in urban environments, there are reflections and other acoustic effects that make it difficult to accurately determine the MB and SW times. This issue will however not be treated in this work. We will instead assume that the detection error is stochastic with a certain distribution. A more thorough analysis of the SW propagation is given in [16].
Of course, the MB and SW (when present) can be used in conjunction with each other. One of the ideas exploited later is to utilize the time difference between the MB and SW detections. This way, the localization is independent of the clock synchronization errors that are always present in wireless sensor networks.
3. Estimation Framework
It is assumed throughout this work that
-
(1)
the coordinates of the microphones are known with negligible error,
-
(2)
the arrival times of the MB and SW at each microphone are measured with significant synchronization error,
-
(3)
the shooter position and aim direction are the sought parameters.
Thus, assume that there are  microphones with known positions
microphones with known positions  in the network detecting the muzzle blast. Without loss of generality, the first
in the network detecting the muzzle blast. Without loss of generality, the first  ones also detect the shock wave. The detected times are denoted by
ones also detect the shock wave. The detected times are denoted by  and
and  , respectively. Each detected time is subject to a detection error
, respectively. Each detected time is subject to a detection error  and
and  , different for all times, and a clock synchronization error
, different for all times, and a clock synchronization error  specific for each microphone. The firing time
specific for each microphone. The firing time  , shooter position
, shooter position  , and shooting direction
, and shooting direction  are unknown parameters. Also the bullet speed
are unknown parameters. Also the bullet speed  and speed of sound
and speed of sound  are unknown. Basic signal models for the detected times as a function of the parameters will be derived in the next section. The notation is summarized in Table 1.
are unknown. Basic signal models for the detected times as a function of the parameters will be derived in the next section. The notation is summarized in Table 1.
The derived signal models will be of the form

where  is a vector with the measured detection times,
is a vector with the measured detection times,  is a nonlinear function with values in
is a nonlinear function with values in  , and where
, and where  represents the unknown parameters apart from
represents the unknown parameters apart from  . The error
. The error  is assumed to be stochastic; see Section 4.5. Given the sensor locations in
is assumed to be stochastic; see Section 4.5. Given the sensor locations in  , nonlinear optimization can be performed to estimate
, nonlinear optimization can be performed to estimate  , using the nonlinear least squares (NLS) criterion:
, using the nonlinear least squares (NLS) criterion:

Here,  denotes the minimizing argument,
denotes the minimizing argument,  the minimum of the function, and
the minimum of the function, and  denotes the
denotes the  -norm, that is,
-norm, that is,  . Whenever
. Whenever  is omitted,
is omitted,  is assumed. The loss function norm
is assumed. The loss function norm  is chosen by consideration of the expected error characteristics. Numerical optimization, for instance, the Gauss-Newton method, can here be applied to get the NLS estimate.
is chosen by consideration of the expected error characteristics. Numerical optimization, for instance, the Gauss-Newton method, can here be applied to get the NLS estimate.
In the next section it will become clear that the assumed unknown firing time and the inverse speed of sound enter the model equations linearly. To exploit this fact we identify a sublinear structure in the signal model and apply the weighted least squares method to the parameters appearing linearly, the separable least squares method; see, for instance [17]. By doing so, the NLS search space is reduced which in turn significantly reduces the computational burden. For that reason, the signal model (1) is rewritten as

Note that  enters linearly here. The NLS problem can then be formulated as
enters linearly here. The NLS problem can then be formulated as

Since  enters linearly, it can be solved for by linear least squares (the arguments of
enters linearly, it can be solved for by linear least squares (the arguments of  and
and  are suppressed for clarity):
are suppressed for clarity):


Here,  is the weighted least squares estimate and
is the weighted least squares estimate and  is the covariance matrix of the estimation error. This simplifies the nonlinear minimization to
is the covariance matrix of the estimation error. This simplifies the nonlinear minimization to

This general separable least squares (SLSs) approach will now be applied to four different combinations of signal models for the MB and SW detection times.
4. Signal Models
4.1. Muzzle Blast Model (MB)
According to the clock at microphone  , the muzzle blast (MB) sound is assumed to reach
, the muzzle blast (MB) sound is assumed to reach  at the time
at the time

The shooter position  and microphone location
and microphone location  are in
are in  , where generally
, where generally  . However, both computational and numerical issues occasionally motivate a simplified plane model with
. However, both computational and numerical issues occasionally motivate a simplified plane model with  . For all
. For all  microphones, the model is represented in vector form as
microphones, the model is represented in vector form as

where


and where  ,
,  , and
, and  are vectors with elements
are vectors with elements  ,
,  , and
, and  , respectively.
, respectively.  is the vector with
is the vector with  ones, where
ones, where  might be omitted if there is no ambiguity regarding the dimension. Furthermore,
might be omitted if there is no ambiguity regarding the dimension. Furthermore,  is
is  -by-
-by- , where each row is a microphone position. Note that the inverse of the speed of sound enters linearly. The
, where each row is a microphone position. Note that the inverse of the speed of sound enters linearly. The  notation indicates that
notation indicates that  is part of a linear relation, as described in the previous section. With
is part of a linear relation, as described in the previous section. With  and
and  , (6) gives
, (6) gives


Here,  depends on
depends on  as given in (9b).
as given in (9b).
This criterion has computationally efficient implementations, that in many applications make the time it takes to do an exhaustive minimization over a, say, 10-meter grid acceptable. The grid-based minimization of course reduces the risk to settle on suboptimal local minimizers, which otherwise could be a risk using greedy search methods. The objective function does, however, behave rather well. Figure 2 visualizes (10a) in logarithmic scale for data from a field trial (the norm is  ). Apparently, there are only two local minima.
). Apparently, there are only two local minima.
4.2. Shock Wave Model (SW)
In general, the bullet follows a ballistic three-dimensional trajectory. In practice, a simpler model with a two-dimensional trajectory with constant deceleration might suffice. Thus, it will be assumed that the bullet follows a straight line with initial speed  ; see Figure 3. Due to air friction, the bullet decelerates; so when the bullet has traveled the distance
; see Figure 3. Due to air friction, the bullet decelerates; so when the bullet has traveled the distance  , for some point
, for some point  on the trajectory, the speed is reduced to
on the trajectory, the speed is reduced to

where  is an assumed known ballistic parameter. This is a rather coarse bullet trajectory model, compared with, for instance, the curvilinear trajectories proposed by [18], but we use it here for simplicity. This model is also a special case of the ballistic model used in [19].
is an assumed known ballistic parameter. This is a rather coarse bullet trajectory model, compared with, for instance, the curvilinear trajectories proposed by [18], but we use it here for simplicity. This model is also a special case of the ballistic model used in [19].
The shock wave from the bullet trajectory propagates at the speed of sound  with angle
with angle  to the bullet heading.
to the bullet heading.  is the Mach angle defined as
is the Mach angle defined as

 is now the point where the shock wave that reaches microphone
is now the point where the shock wave that reaches microphone  is generated. The time it takes the bullet to reach
is generated. The time it takes the bullet to reach  is
is

This time and the wave propagation time from  to
to  sum up to the total time from firing to detection:
sum up to the total time from firing to detection:

according to the clock at microphone  . Note that the variable names
. Note that the variable names  and
and  for notational simplicity have been reused from the MB model. Below, also
for notational simplicity have been reused from the MB model. Below, also  , and
, and  will be reused. When there is ambiguity, a superscript will indicate exactly which entity that is referred to, for instance,
will be reused. When there is ambiguity, a superscript will indicate exactly which entity that is referred to, for instance,  .
.
It is a little bit tedious to calculate  . The law of sines gives
. The law of sines gives

which together with (12) implicitly defines  . We have not found any simple closed form for
. We have not found any simple closed form for  ; so we solve for
; so we solve for  numerically, and in case of multiple solutions we keep the admissible one (which turns out to be unique).
numerically, and in case of multiple solutions we keep the admissible one (which turns out to be unique).  is trivially induced by the shooting direction
is trivially induced by the shooting direction  (and
(and  ,
,  ). Both these angles thus depend on
). Both these angles thus depend on  implicitly.
implicitly.
The vector form of the model is

where

and where row  of
of  is
is

and  is the admissible solution to (12) and (15).
is the admissible solution to (12) and (15).
4.3. Combined Model (MB;SW)
In the MB and SW models, the synchronization error has to be regarded as a noise component. In a combined model, each pair of MB and SW detections depends on the same synchronization error, and consequently the synchronization error can be regarded as a parameter (at least for all sensor nodes inside the SW cone). The total signal model could be fused from the MB and SW models as the total observation vector:

where





4.4. Difference Model (MB-SW)
Motivated by accurate localization despite synchronization errors, we study the MB-SW model:

for  . This rather special model has also been analyzed in [12, 15]. The key idea is that
. This rather special model has also been analyzed in [12, 15]. The key idea is that  is by cancellation independent of both the firing time
is by cancellation independent of both the firing time  and the synchronization error
and the synchronization error  . The drawback, of course, is that there are only
. The drawback, of course, is that there are only  equations (instead of a total of
equations (instead of a total of  ) and the detection error increases,
) and the detection error increases,  . However, when the synchronization errors are expected to be significantly larger than the detection errors, and when also
. However, when the synchronization errors are expected to be significantly larger than the detection errors, and when also  is sufficiently large (at least as large as the number of parameters), this model is believed to give better localization accuracy. This will be investigated later.
is sufficiently large (at least as large as the number of parameters), this model is believed to give better localization accuracy. This will be investigated later.
There are no parameters in (25) that appear linearly everywhere. Thus, the vector form for the MB-SW model can be written as

where

and  and
and  . As before,
. As before,  is the admissible solution to (12) and (15). The MB-SW least squares criterion is
is the admissible solution to (12) and (15). The MB-SW least squares criterion is

which requires numerical optimization. Numerical experiments indicate that this optimization problem is more prone to local minima, compared to (10a) for the MB model; therefore good starting points for the numerical search are essential. One such starting point could, for instance, be the MB estimate  . Initial shooting direction could be given by assuming, in a sense, the worst possible case, that the shooter aims at some point close to the center of the microphone network.
. Initial shooting direction could be given by assuming, in a sense, the worst possible case, that the shooter aims at some point close to the center of the microphone network.
4.5. Error Model
At an arbitrary moment, the detection errors and synchronization errors are assumed to be independent stochastic variables with normal distribution:



For the MB-SW model the error is consequently

Assuming that  in the MB;SW model, the covariance of the summed detection and synchronization errors can be expressed in a simple manner as
in the MB;SW model, the covariance of the summed detection and synchronization errors can be expressed in a simple manner as

Note that the correlation structure of the clock synchronization error  enables estimation of these. Note also that the (assumed known) total error covariance, generally denoted by
enables estimation of these. Note also that the (assumed known) total error covariance, generally denoted by  , dictates the norm used in the weighted least squares criterion.
, dictates the norm used in the weighted least squares criterion.  also impacts the estimation bounds. This will be discussed in the next section.
also impacts the estimation bounds. This will be discussed in the next section.
4.6. Summary of Models
Four models with different purposes have been described in this section.
-
(i)
MB. Given that the acoustic environment enables reliable detection of the muzzle blast, the MB model promises the most robust estimation algorithms. It also allows global minimization with low-dimensional exhaustive search algorithms. This model is thus suitable for initialization of algorithms based on the subsequent models.
-
(ii)
SW. The SW model extends the MB model with shooting angle, bullet speed, and deceleration parameters, which provide useful information for sniper detection applications. The SW is easier to detect in disturbed environments, particularly when the shooter is far away and the bullet passes closely. However, a sufficient number of microphones are required to be located within the SW cone, and the SW measurements alone cannot be used to determine the distance to the shooter.
-
(iii)
MB;SW. The total MB;SW model keeps all information from the observations and should thus provide the most accurate and general estimation performance. However, the complexity of the estimation problem is large.
-
(iv)
MB-SW. All algorithms based on the models above require that the synchronization error in each microphone either is negligible or can be described with a statistical distribution. The MB-SW model relaxes such assumptions by eliminating the synchronization error by taking differences of the two pulses at each microphone. This also eliminates the shooting time. The final model contains all interesting parameters for the problem, but only one nuisance parameter (actual speed of sound, which further may be eliminated if known sufficiently well).
The different parameter vectors in the relation  are summarized in Table 2.
are summarized in Table 2.
 , where the noise models are summarized in (29a), (29b), (29c), (29d), and (29e). The values of the dimensions assume that the set of microphones giving SW observations is a subset of the MB observations.
, where the noise models are summarized in (29a), (29b), (29c), (29d), and (29e). The values of the dimensions assume that the set of microphones giving SW observations is a subset of the MB observations.5. Cramér-Rao Lower Bound
The accuracy of any unbiased estimator  in the rather general model
in the rather general model

is, under not too restrictive assumptions [20], bounded by the Cramér-Rao bound:

where  is Fisher's information matrix evaluated at the correct parameter values
is Fisher's information matrix evaluated at the correct parameter values  . Here, the location
. Here, the location  is for notational purposes part of the parameter vector
is for notational purposes part of the parameter vector  . Also the sensor positions
. Also the sensor positions  can be part of
can be part of  , if these are known only with a certain uncertainty. The Cramér-Rao lower bound provides a fundamental estimation limit for unbiased estimators; see [20]. This bound has been analyzed thoroughly in the literature, primarily for AOA, TOA, and TDOA [21–23].
, if these are known only with a certain uncertainty. The Cramér-Rao lower bound provides a fundamental estimation limit for unbiased estimators; see [20]. This bound has been analyzed thoroughly in the literature, primarily for AOA, TOA, and TDOA [21–23].
The Fisher information matrix for  takes the form
takes the form

The bound is evaluated for a specific location, parameter setting, and microphone positioning, collectively  .
.
The bound for the localization error is

This covariance can be converted to a more convenient scalar value giving a bound on the root mean square error (RMSE) using the trace operator:

The RMSE bound can be used to compare the information in different models in a simple and unambiguous way, which does not depend on which optimization criterion is used or which numerical algorithm that is applied to minimize the criterion.
5.1. MB Case
For the MB case, the entities in (32) are identified by

Note that  is accounted for by the error model. The Jacobian
is accounted for by the error model. The Jacobian  is an
is an  -by-
-by- +2 matrix,
+2 matrix,  being the dimension of
being the dimension of  . The LS solution in (5a) however gives a shortcut to an
. The LS solution in (5a) however gives a shortcut to an  -by-
-by- Jacobian:
Jacobian:

for  , where
, where  ,
,  , and
, and  denote the true (unperturbed) values. For the case
denote the true (unperturbed) values. For the case  and known
and known  , this Jacobian can, with some effort, be expressed explicitly. The equivalent bound is
, this Jacobian can, with some effort, be expressed explicitly. The equivalent bound is

5.2. SW, MB;SW, and MB-SW Cases
The estimation bounds for the SW, MB;SW, and MB-SW cases are analogously to (33), but there are hardly any analytical expressions available. The Jacobian is probably best evaluated by finite difference methods.
5.3. Numerical Example
The really interesting question is how the information in the different models relates to each other. We will study a scenario where 14 microphones are deployed in a sensor network to support camp protection; see Figure 4. The microphones are positioned along a road to track vehicles and around the camp site to detect intruders. Of course, the microphones also detect muzzle blasts and shock waves from gunfire, so shooters can be localized and the shooter's target identified.
A plane model (flat camp site) is assumed,  . Furthermore, it is assumed that
. Furthermore, it is assumed that

and that  m/s,
m/s,  m/s, and
m/s, and  . The scenario setup implies that all microphones detect the shock wave, so
. The scenario setup implies that all microphones detect the shock wave, so  . All bounds presented below are calculated by numerical finite difference methods.
. All bounds presented below are calculated by numerical finite difference methods.
MB Model
The localization accuracy using the MB model is bounded below according to

The root mean square error (RMSE) is consequently bounded according to

Monte Carlo simulations (not described here) indicate that the NLS estimator attains this lower bound for  s. The dash-dotted curve in Figure 5 shows the bound versus
s. The dash-dotted curve in Figure 5 shows the bound versus  for fix
for fix  s. An uncontrolled increase as soon as
s. An uncontrolled increase as soon as  can be noted.
can be noted.
SW Model
The SW model is disregarded here, since the SW detections alone contain no shooter distance information.
MB-SW Model
The localization accuracy using the MB-SW model is bounded according to


The dashed lines in Figure 5 correspond to the RMSE bound for four different values of  . Here, the MB-SW model gives at least twice the error of the MB model, provided that there are no synchronization errors. However, in a wireless network we expect the synchronization error to be 10–100 times larger than the detection error, and then the MB-SW error will be substantially smaller than the MB error.
. Here, the MB-SW model gives at least twice the error of the MB model, provided that there are no synchronization errors. However, in a wireless network we expect the synchronization error to be 10–100 times larger than the detection error, and then the MB-SW error will be substantially smaller than the MB error.
MB;SW Model
The expression for the MB;SW bound is somewhat involved; so the dependence on  is only presented graphically, see Figure 5. The solid curves correspond to the MB;SW RMSE bound for the same four values of
is only presented graphically, see Figure 5. The solid curves correspond to the MB;SW RMSE bound for the same four values of  as for the MB-SW bound. Apparently, when the synchronization error
as for the MB-SW bound. Apparently, when the synchronization error  is large compared to the detection error
is large compared to the detection error  , the MB-SW and MB;SW models contain roughly the same amount of information, and the model having the simplest estimator, that is, the MB-SW model, should be preferred. However, when the synchronization error is smaller than 100 times the detection error, the complete MB;SW model becomes more informative.
, the MB-SW and MB;SW models contain roughly the same amount of information, and the model having the simplest estimator, that is, the MB-SW model, should be preferred. However, when the synchronization error is smaller than 100 times the detection error, the complete MB;SW model becomes more informative.
These results are comparable with the analysis in [12, Figure 4a], where an example scenario with 6 microphones is considered.
5.4. Summary of the CRLB Analysis
The synchronization error level in a wireless sensor network is usually a matter of design tradeoff between performance and battery costs required by synchronization mechanisms. Based on the scenario example, the CRLB analysis is summarized with the following recommendations.
-
(i)
If
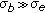 , then the MB-SW model should be used.
, then the MB-SW model should be used. -
(ii)
If
 is moderate, then the MB;SW model should be used.
is moderate, then the MB;SW model should be used. -
(iii)
Only if
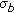 is very small (
is very small (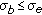 ), the shooting direction is of minor interest, and performance may be traded for simplicity, then the MB model should be used.
), the shooting direction is of minor interest, and performance may be traded for simplicity, then the MB model should be used.
6. Experimental Data
A field trial to collect acoustic data on nonmilitary small arms fire is conducted. 10 microphones are placed around a fictitious camp; see Figure 6. The microphones are placed close to the ground and wired to a common recorder with 16-bit sampling at 48 kHz. A total of 42 rounds are fired from three positions and aimed at a common cardboard target. Three rifles and one pistol are used; see Table 3. Four rounds are fired of each armament at each shooter position, with two exceptions. The pistol is only used at position three. At position three, six instead of four rounds of 308 W are fired. All ammunition types are supersonic. However, when firing from position three, not all microphones are subjected to the shock wave.
Light wind, no clouds, and around  C are the weather conditions. Little or no acoustic disturbances are present. The terrain is rough. Dense woods surround the test site. There is light bush vegetation within the site. Shooter position 1 is elevated some 20 m; otherwise spots are within
C are the weather conditions. Little or no acoustic disturbances are present. The terrain is rough. Dense woods surround the test site. There is light bush vegetation within the site. Shooter position 1 is elevated some 20 m; otherwise spots are within  5 m of a horizontal plane. Ground truth values of the positions are determined with less relative error than 1 m, except for shooter position 1, which is determined with 10 m accuracy.
5 m of a horizontal plane. Ground truth values of the positions are determined with less relative error than 1 m, except for shooter position 1, which is determined with 10 m accuracy.
6.1. Detection
The MB and SW are detected by visual inspection of the microphone signals in conjunction with filtering techniques. For shooter positions 1 and 2, the shock wave detection accuracy is approximately  s, and the muzzle blast error
s, and the muzzle blast error  is slightly worse. For shooting position 3 the accuracies are generally much worse, since the muzzle blast and shock wave components become intermixed in time.
is slightly worse. For shooting position 3 the accuracies are generally much worse, since the muzzle blast and shock wave components become intermixed in time.
6.2. Numerical Setup
For simplicity, a plane model is assumed. All elevation measurements are ignored and  and
and  . Localization using the MB model (7) is done by minimizing (10a) over a 10 m grid well covering the area of interest, followed by numerical minimization.
. Localization using the MB model (7) is done by minimizing (10a) over a 10 m grid well covering the area of interest, followed by numerical minimization.
Localization using the MB-SW model (25) is done by numerically minimizing (28). The objective function is subject to local optima; therefore the more robust muzzle blast localization  is used as an initial guess. Furthermore, the direction from
is used as an initial guess. Furthermore, the direction from  toward the mean point of the microphones (the camp) is used as initial shooting direction
toward the mean point of the microphones (the camp) is used as initial shooting direction  . Initial bullet speed is
. Initial bullet speed is  m/s and initial speed of sound is
m/s and initial speed of sound is  m/s.
m/s.  is used, which is a value derived from the 308 Winchester ammunition ballistics.
is used, which is a value derived from the 308 Winchester ammunition ballistics.
6.3. Results
Figure 7 shows, at three enlarged parts of the scene, the resulting position estimates based on the MB model (blue crosses) and based on the MB-SW (squares). Apparently, the use of the shock wave significantly improves localization at positions 1 and 2, while rather the opposite holds at position 3. Figure 8 visualizes the shooting direction estimates,  . Estimate root mean square errors (RMSEs) for the three shooter positions, together with the theoretical bounds (34), are given in Table 4. The practical results indicate that the use of the shock wave from distant shooters cut the error by at least 75%.
. Estimate root mean square errors (RMSEs) for the three shooter positions, together with the theoretical bounds (34), are given in Table 4. The practical results indicate that the use of the shock wave from distant shooters cut the error by at least 75%.
 against the target,
against the target,  , not with respect to the true direction
, not with respect to the true direction  . This way the ability to identify the target is assessed.
. This way the ability to identify the target is assessed.6.3.1. Synchronization and Detection Errors
Since all microphones are recorded by a common recorder, there are actually no timing errors due to inaccurate clocks. This is of course the best way to conduct a controlled experiment, where any uncertainty renders the dataset less useful. From experimental point of view, it is then simple to add synchronization errors of any desired magnitude off-line. On the dataset at hand, this is however work under progress. At the moment, there are apparently other sources of error, worth identifying. It should however be clarified that in the final wireless sensor product, there will always be an unpredictable clock error. As mentioned, detection errors are present, and the expected level of these (80  s) is used for bound calculations in Table 4. It is noted that the bounds are in level with, or below, the positioning errors.
s) is used for bound calculations in Table 4. It is noted that the bounds are in level with, or below, the positioning errors.
There are at least two explanations for the bad performance using the MB-SW model at shooter position 3. One is that the number of microphones reached by the shock wave is insufficient to make accurate estimates. There are four unknown model parameters, but for the relatively low speed of pistol ammunition, for instance, only one microphone has a valid shock wave detection. Another explanation is that the increased detection uncertainty (due to SW/MB intermix) impacts the MB-SW model harder, since it relies on accurate detection of both the MB and SW.
6.3.2. Model Errors
No doubt, there are model inaccuracies both in the ballistic and in the acoustic domain. To that end, there are meteorological uncertainties out of our control. For instance, looking at the MB-SW localizations around shooter position 1 in Figure 7 (squares), three clusters are identified that correspond to three ammunition types with different ballistic properties; see the RMSE for each ammunition and position in Table 3. This clustering or bias more likely stems from model errors than from detection errors and could at least partially explain the large gap between theoretical bound and RMSE in Table 4. Working with three-dimensional data in the plane is of course another model discrepancy that could have greater impact than we first anticipated. This will be investigated in experiments to come.
6.3.3. Numerical Uncertainties
Finally, we face numerical uncertainties. There is no guarantee that the numerical minimization programs we have used here for the MB-SW model really deliver the global minimum. In a realistic implementation, every possible a priori knowledge and also qualitative analysis of the SW and MB signals (amplitude, duration, caliber classification, etc.) together with basic consistency checks are used to reduce the search space. The reduced search space may then be exhaustively sampled over a grid prior to the final numerical minimization. Simple experiments on an ordinary desktop PC indicate that with an efficient implementation, it is feasible to, within the time frame of one second, minimize any of the described model objective functions over a discrete grid with  points. Thus, by allowing—say—one second extra of computation time, the risk for hitting a local optima could be significantly reduced.
points. Thus, by allowing—say—one second extra of computation time, the risk for hitting a local optima could be significantly reduced.
7. Conclusions
We have presented a framework for estimation of shooter location and aiming angle from wireless networks where each node has a single microphone. Both the acoustic muzzle blast (MB) and the ballistic shock wave (SW) contain useful information about the position, but only the SW contains information about the aiming angle. A separable nonlinear least squares (SNLSs) framework was proposed to limit the parametric search space and to enable the use of global grid-based optimization algorithms (for the MB model), eliminating potential problems with local minima.
For a perfectly synchronized network, both MB and SW measurements should be stacked into one large signal model for which SNLS is applied. However, when the synchronization error in the network becomes comparable to the detection error for MB and SW, the performance quickly deteriorates. For that reason, the time difference of MB and SW at each microphone is used, which automatically eliminates any clock offset. The effective number of measurements decreases in this approach, but as the CRLB analysis showed, the root mean square position error is comparable to that of the ideal stacked model, at the same time as the synchronization error distribution may be completely disregarded.
The bullet speed occurs as nuisance parameters in the proposed signal model. Further, the bullet retardation constant was optimized manually. Future work will investigate if the retardation constant should also be estimated, and if these two parameters can be used, together with the MB and SW signal forms, to identify the weapon and ammunition.
References
Bédard J, Paré S: Ferret, a small arms' fire detection system: localization concepts. Sensors, and Command, Control, Communications, and Intelligence (C31) Technologies for Homeland Defense and Law Enforcement II, 2003, Proceedings of SPIE 5071: 497-509.
Mazurek JA, Barger JE, Brinn M, Mullen RJ, Price D, Ritter SE, Schmitt D: Boomerang mobile counter shooter detection system. Sensors, and C3I Technologies for Homeland Security and Homeland Defense IV, 2005, Bellingham, Wash, USA, Proceedings of SPIE 5778: 264-282.
Crane D: Ears-MM soldier-wearable gun-shot/sniper detection and location system. Defence Review, 2008
PILAR Sniper Countermeasures System November 2008, http://www.canberra.com
Millet J, Balingand B: Latest achievements in gunfire detection systems. Proceedings of the of the RTO-MP-SET-107 Battlefield Acoustic Sensing for ISR Applications, 2006, Neuilly-sur-Seine, France
Volgyesi P, Balogh G, Nadas A, et al.: Shooter localization and weapon classification with soldier-wearable networked sensors. Proceedings of the 5th International Conference on Mobile Systems, Applications, and Services (MobiSys '07), 2007, San Juan, Puerto Rico
Saxena A, Ng AY: Learning Sound Location from a single microphone. Proceedings of the IEEE International Conference on Robotics and Automation (ICRA '09), May 2009, Kobe, Japan 1737-1742.
Conner WS, Chhabra J, Yarvis M, Krishnamurthy L: Experimental evaluation of synchronization and topology control for in-building sensor network applications. Proceedings of the 2nd ACM International Workshop on Wireless Sensor Networks and Applications (WSNA '03), September 2003, San Diego, Calif, USA 38-49.
Younis O, Fahmy S: A scalable framework for distributed time synchronization in multi-hop sensor networks. Proceedings of the 2nd Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks (SECON '05), September 2005, Santa Clara, Calif, USA 13-23.
Elson J, Estrin D: Time synchronization for wireless sensor networks. Proceedings of the International Parallel and Distributed Processing Symposium, 2001
Simon G, Maróti M, Lédeczi Á, et al.: Sensor network-based countersniper system. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys '04), November 2004, Baltimore, Md, USA 1-12.
Whipps GT, Kaplan LM, Damarla R: Analysis of sniper localization for mobile, asynchronous sensors. Signal Processing, Sensor Fusion, and Target Recognition XVIII, 2009, Proceedings of SPIE 7336:
Danicki E: Acoustic sniper localization. Archives of Acoustics 2005, 30(2):233-245.
Kaplan LM, Damarla T, Pham T: Qol for passive acoustic gunfire localization. Proceedings of the 5th IEEE International Conference on Mobile Ad-Hoc and Sensor Systems (MASS '08), 2008, Atlanta, Ga, USA 754-759.
Lindgren D, Wilsson O, Gustafsson F, Habberstad H: Shooter localization in wireless sensor networks. Proceedings of the 12th International Conference on Information Fusion (FUSION '09), 2009, Seattle, Wash, USA 404-411.
Stoughton R: Measurements of small-caliber ballistic shock waves in air. Journal of the Acoustical Society of America 1997, 102(2):781-787. 10.1121/1.419904
Gustafsson F: Statistical Sensor Fusion. Studentlitteratur, Lund, Sweden; 2010.
Danicki E: The shock wave-based acoustic sniper localization. Nonlinear Analysis: Theory, Methods & Applications 2006, 65(5):956-962. 10.1016/j.na.2005.07.043
Lo KW, Ferguson BG: A ballistic model-based method for ranging direct fire weapons using the acoustic muzzle blast and shock wave. Proceedings of the International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP '08), December 2008 453-458.
Kay S: Fundamentals of Signal Processing: Estimation Theory. Prentice Hall, Upper Saddle River, NJ, USA; 1993.
Patwari N, Hero AO III, Perkins M, Correal NS, O'Dea RJ: Relative location estimation in wireless sensor networks. IEEE Transactions on Signal Processing 2003, 51(8):2137-2148. 10.1109/TSP.2003.814469
Gezici S, Tian Z, Giannakis GB, Kobayashi H, Molisch AF, Poor HV, Sahinoglu Z: Localization via ultra-wideband radios: a look at positioning aspects of future sensor networks. IEEE Signal Processing Magazine 2005, 22(4):70-84.
Gustafsson F, Gunnarsson F: Possibilities and fundamental limitations of positioning using wireless communication networks measurements. IEEE Signal Processing Magazine 2005, 22: 41-53.
Acknowledgment
This work is funded by the VINNOVA supported Centre for Advanced Sensors, Multisensors and Sensor Networks, FOCUS, at the Swedish Defence Research Agency, FOI.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lindgren, D., Wilsson, O., Gustafsson, F. et al. Shooter Localization in Wireless Microphone Networks. EURASIP J. Adv. Signal Process. 2010, 690732 (2010). https://doi.org/10.1155/2010/690732
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/690732



 , and the speed of sound c, the time it takes from firing the gun to detecting the shock wave can be calculated.
, and the speed of sound c, the time it takes from firing the gun to detecting the shock wave can be calculated.

 , and for different levels of detection error
, and for different levels of detection error  .
.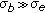 , then the MB-SW model should be used.
, then the MB-SW model should be used. is moderate, then the MB;SW model should be used.
is moderate, then the MB;SW model should be used.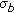 is very small (
is very small (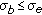 ), the shooting direction is of minor interest, and performance may be traded for simplicity, then the MB model should be used.
), the shooting direction is of minor interest, and performance may be traded for simplicity, then the MB model should be used.

 based on the MB model and on the MB-SW model. The diagrams are enlargements of the interesting areas around the shooter positions. The dashed lines identify the shooting directions.
based on the MB model and on the MB-SW model. The diagrams are enlargements of the interesting areas around the shooter positions. The dashed lines identify the shooting directions.